自行弹炮结合防空武器间信息传递误差研究
2022-04-20鲍晨希丁天宝何浩何朝
鲍晨希,丁天宝,何浩,何朝
(西北机电工程研究所,陕西 咸阳 712099)
自行弹炮结合防空武器系统[1]一般以连为基本建制装备部队,一个连套装备通常由一台连指挥车、若干台自行弹炮结合武器(以下简称“战车”)和若干保障装备组成。自行弹炮结合防空武器系统主要有3种作战方式:一是在连指挥车指挥下的连建制作战;二是两台以上战车实施的主从作战;三是单台战车实施的自主作战。
战车是实施作战的主体,其作战流程的主要环节为:目标搜索、目标跟踪、火控解算、火力打击。就这4个环节来说,前面的环节是后面工作的前提;换句话说,如果前面环节的功能出了问题,则后续的功能也就无法正常进行。笔者通过研究火控组网解决以下几个问题:借用连指挥车或其他战车目标搜索信息,解决本战车目标搜索功能缺失情况下的目标搜索问题;借用其他战车目标跟踪信息,解决本战车目标跟踪功能缺失情况下的目标跟踪问题;借用其他战车火控解算信息,解决本战车火控解算功能缺失情况下的火控诸元解算问题。
火控组网信息在传递和处理过程中,非线性坐标变换使火控组网信息误差变大,信息传递过程中的数据时延导致滞后误差[2-3],这些误差导致火控组网所传递的数据精度降低。因此,需要对火控组网信息传递中误差的变化规律进行分析,以提高火控组网中所传递信息的精度。
本文的火控组网指主从车点对点传输下的信息共享过程,笔者主要研究信息传递过程中目标搜索数据在传递后误差的变化规律及减小方法。目标搜索数据误差由系统误差和随机误差两部分组成。系统误差可以通过统计方法寻找误差变化规律后进行补偿,而随机误差由于其随机性无法被静态补偿。笔者以火控组网中主从模式搜索信息共享过程为例对随机误差部分的引入和传递进行建模分析,同时将数据传输导致的时延误差加入误差传递模型,在误差传递模型的基础上寻找合适的方法减小时延带来的数据滞后并减小随机误差,提高搜索信息传递和共享的精度。
1 火控组网原理
首先,对火控组网中涉及的数据进行定义:搜索信息(DS,εS,βS)为搜索雷达斜距离、高低角和方位角,(ΔDS,ΔεS,ΔβS)为对应量测误差;跟踪信息(DR,εR,βR)为跟踪雷达斜距离、高低角和方位角,(ΔDR,ΔεR,ΔβR)为对应量测误差;火控解算信息(εtc,βtc,tf)为火控方位、高低和弹飞时间;车体姿态信息(K,ψ,θ)为车体方位角、横摇角和纵摇角,(ΔK,Δψ,Δθ)为对应量测误差;车体位置信息(x0,y0,z0)为车体在固定坐标系下的直角坐标分量,(Δx0,Δy0,Δz0)为对应量测误差。火控组网原理如图1所示。
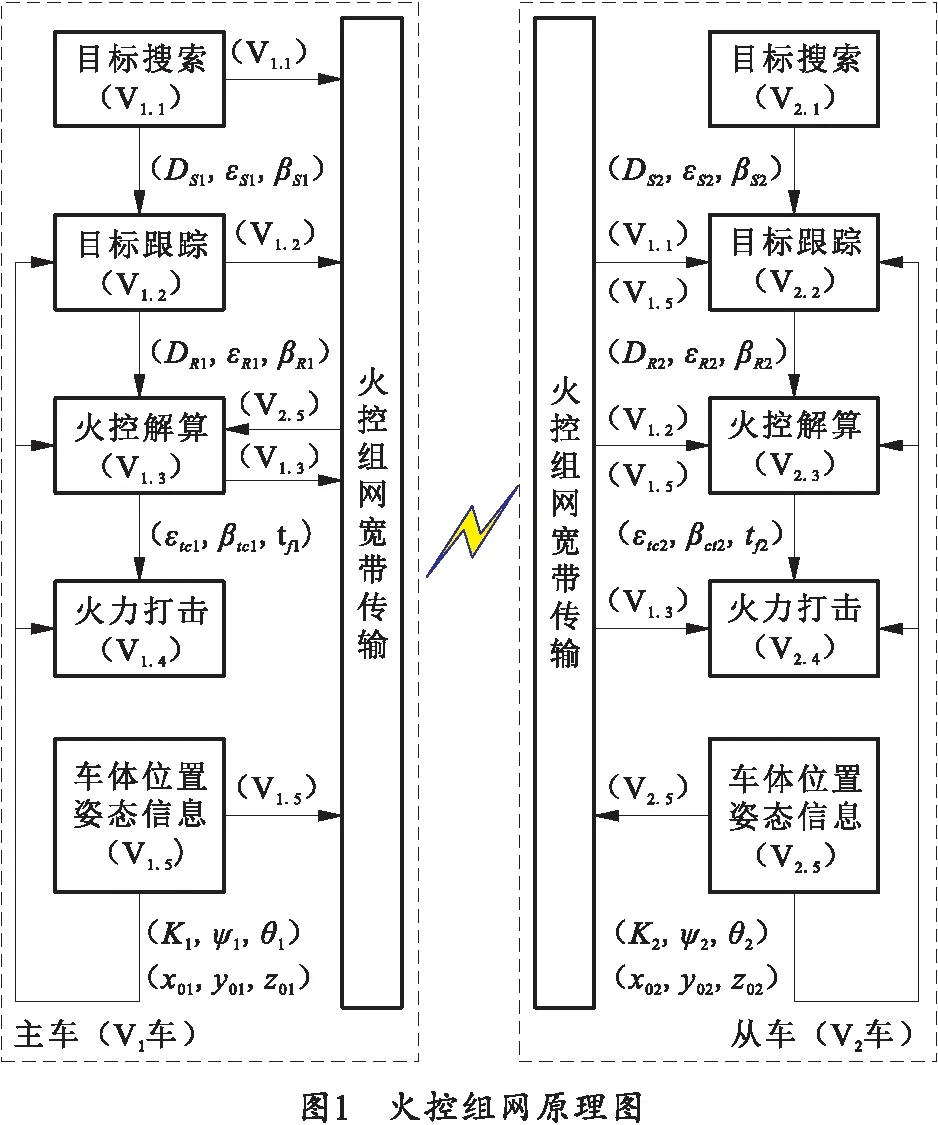
图1描述了单一战车自主作战流程的主要环节;分别解释了火控组网中搜索信息共享、跟踪信息共享和火控解算信息共享发生在战车作战流程的哪一环节下以及共享的信息所包含的数据。
1)火控组网搜索信息共享原理。火控组网搜索信息共享指V2车无法完成V2.1环节时,可以通过无线网络接收V1车V1.1和V1.5环节获取的数据,将该数据处理后作为V2车V2.1环节的输出引导V2车转入V2.2环节。
2)火控组网跟踪信息共享原理。火控组网搜索信息共享指V2车无法完成V2.2环节时,可以通过无线网络接收V1车V1.2和V1.5环节获取的数据,将该数据处理后作为V2车V2.2环节的输出引导V2车转入V2.3环节。
3)火控组网火控解算信息共享原理。火控组网火控解算信息共享指V2车无法完成V2.3环节时,可以通过无线网络将V2车V2.5环节获取的数据传送给V1车;V1车通过无线网络接收V2车V2.5环节获取的数据后,结合自身V1.2和V1.5环节获取的数据替V2车完成V2.3环节,并将该环节的计算结果通过无线网络传输回V2车引导V2车转入V2.4环节。
2 火控组网信息传递数学模型
2.1 坐标系、转换关系及变量定义
笔者参考自行弹炮结合防空武器系统对坐标系的通用定义[1],在该定义基础上对使用到的坐标转换矩阵进行符号定义。主要用到的坐标系有固定坐标系OXYZ,车体坐标系OctXctYctZct及车体球坐标系(D,ε,β)。设由车体坐标系向固定坐标系转换时涉及横滚角ψ和纵摇角θ的转换矩阵为A(ψ,θ),涉及航向角K的转换矩阵为B(k),由车体球坐标系向车体坐标系转换的矩阵函数为H(D,ε,β),由车体坐标系向车体球坐标系转换的矩阵函数为Z(xct,yct,zct)。
火控组网信息传递数学模型推导使用的变量定义如下:
t1(t)=[D1(t)ε1(t)β1(t)]T:t时刻主车车体球坐标系下的目标信息真值;
tct1(t)=[xct1(t)yct1(t)zct1(t)]T:t时刻主车车体坐标系下的目标信息真值;
t(t)=[x(t)y(t)z(t)]T:t时刻固定坐标系下的目标信息真值;
tct2(t)=[xct2(t)yct2(t)zct2(t)]T:t时刻从车车体坐标系下的目标信息真值;
t2(t)=[D2(t)ε2(t)β2(t)]T:t时刻从车车体球坐标系下的目标信息真值;
ta1(t)=[k1(t)ψ1(t)θ1(t)]T:t时刻主车车体姿态信息真值;
t01(t)=[x01(t)y01(t)z01(t)]T:t时刻主车位置信息真值;
ta2(t)=[k2(t)ψ2(t)θ2(t)]T:t时刻从车车体姿态信息真值;
t02(t)=[x02(t)y02(t)z02(t)]T:t时刻从车位置信息真值。
2.2 火控组网信息传递数学模型
为实现火控组网共享,需对待共享信息进行处理,使一战车获取的数据可以被其他战车使用,这是火控组网中的信息传递过程。在没有误差的理想条件下,火控组网信息传递的核心模型为待共享信息从主车车体坐标系转换至从车车体坐标系的数学模型,转换步骤为
1)被传递信息从主车车体球坐标系下转换至主车车体坐标系下,计算公式为
tct1(t)=H(D1(t),ε1(t),β1(t)).
(1)
2)被传递信息从主车车体坐标系下转换至固定坐标系下,计算公式为
t(t)=B(k1(t))A(ψ1(t),θ1(t))tct1(t)+t01(t).
(2)
3)被传递信息从固定坐标系下转换至从车车体坐标系下,计算公式为
tct2(t)=A-1(ψ2(t),θ2(t))B-1(k2(t))
[t(t)-t02(t)].
(3)
4)被传递信息从从车车体坐标系下转换至从车车体球坐标系下,计算公式为
t2(t)=Z(xct2(t),yct2(t),zct2(t)).
(4)
联立式(1)~(4)即可得到火控组网信息传递的数学模型。
3 火控组网信息传递误差分析
3.1 火控组网信息传递误差源分析
对火控组网中共享信息传递流程进行分析,目标信息从主车传递至从车过程中误差源[4]引入过程如图2所示。
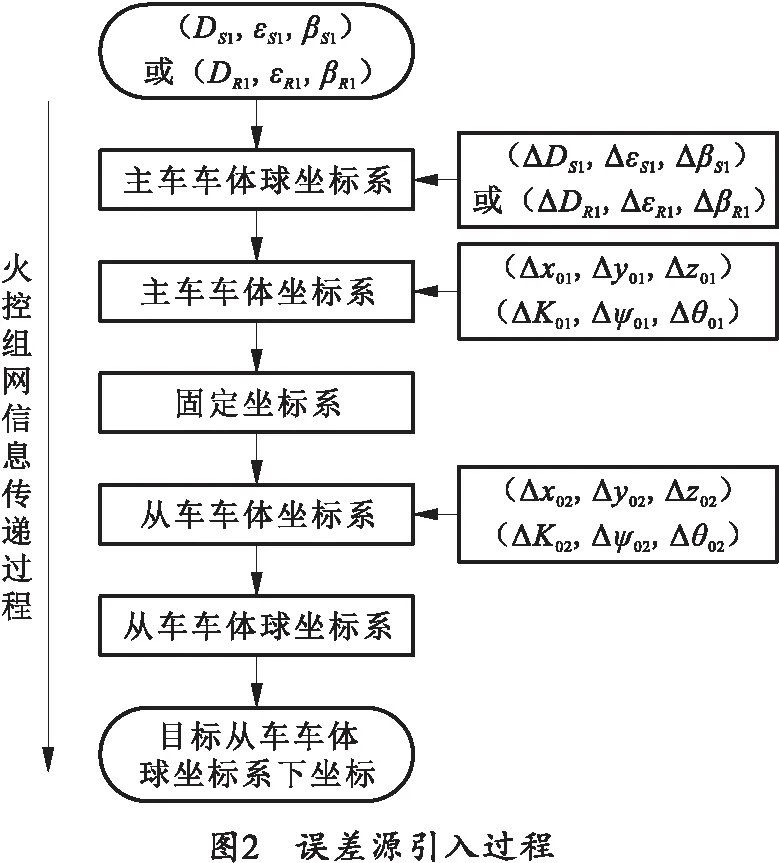
3.2 火控组网信息传递误差模型
根据坐标转换公式和误差源引入过程,利用函数误差传递公式对搜索信息传递误差建模[5-7]。模型推导使用的变量定义如下:
Δt:信息从主车传递至从车的时延;
Δt1(t)=[ΔD1(t)Δε1(t)Δβ1(t)]T:t时刻主车车体球坐标系下的目标信息量测误差;
Δtct1(t)=[Δxct1(t)Δyct1(t)Δzct1(t)]T:t时刻主车车体坐标系下的目标传递误差;
Δt(t)=[Δx(t)Δy(t)Δz(t)]T:t时刻固定坐标系下的目标传递误差;
Δtct2(t)=[Δxct2(t)Δyct2(t)Δzct2(t)]T:t时刻从车车体坐标系下的目标传递误差;
Δt2(t)=[ΔD2(t)Δε2(t)Δβ2(t)]T:t时刻从车车体球坐标系下的目标传递误差;
Δta1(t)=[Δk1(t)Δψ1(t)Δθ1(t)]T:t时刻主车车体姿态信息的量测误差;
Δt01(t)=[Δx01(t)Δy01Δz01(t)]T:t时刻主车位置信息的量测误差;
Δta2(t)=[Δk2(t)Δψ2(t)Δθ2(t)]T:t时刻从车车体姿态信息的量测误差;
Δt02(t)=[Δx02(t)Δy02Δz02(t)]T:t时刻从车位置信息的量测误差。
假设信息从主车传递至从车的时延Δt=0,结合2.2节的火控组网信息传递数学模型建立无时延传递误差模型:
(5)
(6)
(7)
(8)
联立式(5)~(8)即可得到无时延传递误差模型。
实际情况下,信息从主车传递至从车时存在传输时延Δt,传输时延Δt主要包括主车搜索雷达获取信息后通过CAN总线传输给主车宽带车载台的时延Δt1,主车宽带车载台通过无线网络向从车宽带车载台传输的时延Δt2和从车宽带车载台接收信息后通过CAN总线向从车信息处理分系统传输的时延Δt3。其中CAN总线的特性决定了传输时延Δt1、Δt3是固定时延,由于主从车宽带车载台开机时间差异以及内部时钟时差的共同作用,无线网络传输时延Δt2具有随机性;显然Δt=Δt1+Δt2+Δt3,因此主从车间的信息传输时延为随机时延。t时刻时从车接收的数据为t-Δt时刻主车获取的数据,因此建立传递误差模型时t时刻主车车体球坐标系下的目标信息量测误差应表示为
同理可得t时刻主车车体姿态信息和位置信息的量测误差表达式。
同时t时刻从车从主车接收的的数据t1(t)、ta1(t)、t01(t)时标应改为t1(t-Δt)、ta1(t-Δt)、t01(t-Δt);将以上向量回代至上文建立的无时延传递误差模型,得到带时延的传递误差模型。
3.3 火控组网信息传递误差变化规律分析
分别分析目标信息量测误差、主从车方位姿态误差和主从车位置误差对共享信息传递后误差变化的影响规律。
设直角坐标系XOY上有以A(x1,y1)、B(x2,y2)为极点,以过极点平行于X轴正方向的射线为极轴的两个极坐标系,坐标系定义如图3所示。
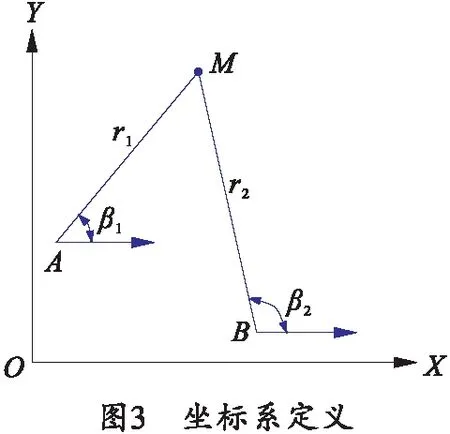
设目标点在极坐标系A下的理论坐标为(r1,β1),误差为(Δr1,Δβ1);通过坐标间的数学关系建立目标点信息从极坐标系A传递至极坐标系B的误差传递模型,考察主从车相对位置关系对共享信息传递误差的影响,模型的数学表达式为
(9)
分析式(9)可知,信息传递后的误差是传递前目标信息斜距离量测误差和角度量测误差的加权合,权重和A、B与目标连线的夹角的角度差及斜距离有关,即与A、B间的相对位置关系有关;且角度差越大,目标离A越远时传递后的信息误差越大。可知由于A、B不在同一物理位置上导致传递过程中对原始量测误差在两个维度信息上的重新分配,这一现象会导致信息传递后各维度信息量测误差发生变化影响信息的精度,因此主车的数据未经处理直接转换至从车很可能导致数据不满足使用需求,需要在转换前先对误差进行处理。
设直角坐标系XOY上两极坐标系极点与O重合,极轴分别为与OX轴夹角为α1、α2的射线,坐标系定义如图4所示。

设目标点在极坐标系A下的理论坐标为(r1,β1),极坐标系A、B极轴与OX轴夹角误差分别为Δα1、Δα2;通过坐标间的数学关系建立目标点信息从极坐标系A传递至极坐标系B的误差传递模型,考察主从车姿态量测误差对共享信息传递误差的影响,模型的数学表达式为
(10)
分析式(10)可知,在主从车位置接近时,单纯的车体姿态量测误差不会影响搜索信息传递后斜距离的误差,但角度误差有可能会叠加,对角度误差取标准差可知角度误差的波动幅度会由于主从车车体姿态量测误差的叠加而变大。因此应在姿态量测信息参与坐标转换前对其进行滤波。
沿用图4所定义坐标系,设目标点在极坐标系A下的理论坐标为(r1,β1),在直角坐标系下与OX轴的夹角为θ,极坐标系A、B极点与O点位移误差分别为(Δx01,Δy01)、(Δx02,Δy02);通过坐标间的数学关系建立目标点信息从极坐标系A传递至极坐标系B的误差传递模型,考察主从车位置量测误差对共享信息传递误差的影响,模型的数学表达式为
(11)
分析式(11)可知,主从车位置信息量测误差会导致传递后误差的变化,对传递后误差取标准差可知传递后误差的波动幅度会由于主从车车体位置量测误差的叠加而变大。因此应在位置量测信息参与坐标转换前对其进行滤波。
4 基于卡尔曼滤波的误差抑制
对于主从车的姿态信息和位置信息的量测误差,建立相应的线性状态空间模型,使用线性卡尔曼滤波[8]减小随机误差后再用于坐标转换过程。由于主车搜索雷达获取的目标量测信息无法直接建立状态转移方程;故先在固定坐标系上建立目标状态转移方程,再结合坐标系间转换矩阵建立观测方程,采用扩展卡尔曼滤波[9]减小目标信息量测误差,状态方程的输出作为目标量测信息从主车车体球坐标系转换至固定坐标系下滤波后的坐标信息及目标在固定坐标系下的运动参数。由3.2节的分析可知,主从车间信息传输时延为随机时延,即从车获取主车数据的时间间隔是随机的,但被传输的搜索数据本身是以20 ms为间隔均匀获取的,满足卡尔曼滤波数据点等间隔的要求。因此在数据处理时,从车可以对获取的数据进行卡尔曼滤波,但滤波后的数据与从车当前时间的时差是随机的,为获得精确的传输时延估计用于将滤波后目标在固定坐标系下的坐标信息外推至当前时间点,需利用GPS授时对主从车宽带车载台进行时统,再结合CAN总线传输的固定时延给共享搜索信息打上时间戳,通过时间戳计算总传输时延。从车从主车接收目标搜索信息、主车姿态及位置信息和时间同步信息后,坐标转换及滤波外推处理流程如图5所示。
主从车车体方位姿态量测信息及车体位置量测信息状态空间模型在静止状态下结构相同参数不同,状态转移方程及观测方程为
(12)


建立好状态空间模型后应用线性卡尔曼滤波器对这两种量测误差进行修正。
对目标位置信息建立空间状态模型,状态转移方程及观测方程为
(13)
式中:
X(k)=[x(k)y(k)z(k)vx(t)vy(k)vz(k)]T,为目标在固定坐标系下的位置信息及速度信息,速度信息的初值可结合航迹起始的一串连续点进行计算;Y(k)=[D(k)ε(k)β(k)]T,为主车搜索雷达获取的目标信息观测值;V(k)为主车搜索雷达的量测误差,是均值为0、方差阵为R的不相关高斯噪声,即E[V(k)VT(j)]=Rδkj,k≠j,δkk=1,δkj=0;E(V(t))=[0 0 0]。
观测值Y(k)与状态X(k)的映射关系表示为
Y(k)=Z(xct1(k),yct1(k),zct1(k)),
(14)
(15)
联立式(14)、(15)即可得h(k,X(k))的表达式。由于观测方程是非线性的,因此先对观测方程进行线性化再使用线性卡尔曼滤波方法进行滤波。对观测方程在当前状态的滤波值处做一阶泰勒展开,保留线性项,线性化后的观测方程表达式为
Y′(k)=H(k)X(k)+y(k)+V(k).
(16)
令Xct1(k)=[xct1(k)yct1(k)zct1(k)],X′(k)=[x(k)y(k)z(k)],H(k)的表达式为
(17)
从车对接收的目标搜索信息滤波后,目标搜索信息从主车车体坐标系转换至固定坐标系,并且减小了随机误差的波动幅度,由于数据传输存在时延Δt,故当前时刻t滤波后固定坐标系上的目标信息X′(t)实为t-Δt时刻的目标信息X(t-Δt),利用滤波后精度更高的目标位置信息[x(t-Δt)y(t-Δt)z(t-Δt)]T和目标速度信息[vx(t-Δt)vy(t-Δt)vz(t-Δt)]T外推出当前时刻t时的目标位置信息,计算公式为
(18)
经过滤波和外推后的目标搜索信息减小了空间和时间上的误差,再通过坐标变换矩阵将搜索信息从固定坐标系转换至从车车体坐标系,即可引导从车转入对目标的跟踪。
5 火控组网搜索信息共享误差仿真
以火控组网搜索信息共享过程为例进行仿真,在仿真中引入各类量测误差[10],观察搜索信息共享后误差的变化规律。
假定主车与从车皆处于静止状态,主车方位角、横滚角和纵摇角分别为(k1,ψ1,θ1)=(15°,-5°,10°),在固定坐标系下的位置为(x01,y01,z01)=(50 m,75 m,10 m);从车方位角、横滚角和纵摇角分别为(k2,ψ2,θ2)=(-15°,10°,-5°),在固定坐标系下的位置为(x02,y02,z02)=(25 m,100 m,-5 m)。目标在固定坐标系上从点(4 000 m,4 500 m,3 000 m)处起始,以(-300 m/s,-400 m/s,-100 m/s)的初速度做匀速直线运动,主车搜索雷达对目标进行探测,并将目标信息共享给从车。
假设主从车所有量测误差均为服从高斯分布的随机误差;搜索雷达距离误差标准差为60 m,高低角误差标准差为0.4°,方位角误差标准差为0.5°;主从车位置误差标准差为10 m,主从车车体航向角、纵摇角和横滚角误差标准差为1密位,数据传输时延为100 ms。
对主车搜索雷达原始量测误差进行仿真,引入主从车车体位置及姿态量测误差,在主车时间轴上对搜索信息传递过程进行仿真,得到搜索信息传输前后的误差变化,仿真结果如图6~8所示。



由图6~8可知,主车获取的目标搜索信息经过搜索信息传递过程后,由于主从车的位置不同及车体位置、姿态量测误差和数据传输时延的引入导致搜索信息传递后的波动幅度明显变大,无法满足从车使用该信息转入对目标跟踪的需求。
将第4节中建立好的滤波器模型引入火控组网搜索信息共享流程中,进行滤波及外推后目标位置信息从主车共享至从车后距离、俯仰角和方位角的误差仿真,利用观测值的前80个点使用线性回归法初始化滤波器。仿真结果如图9~11所示。
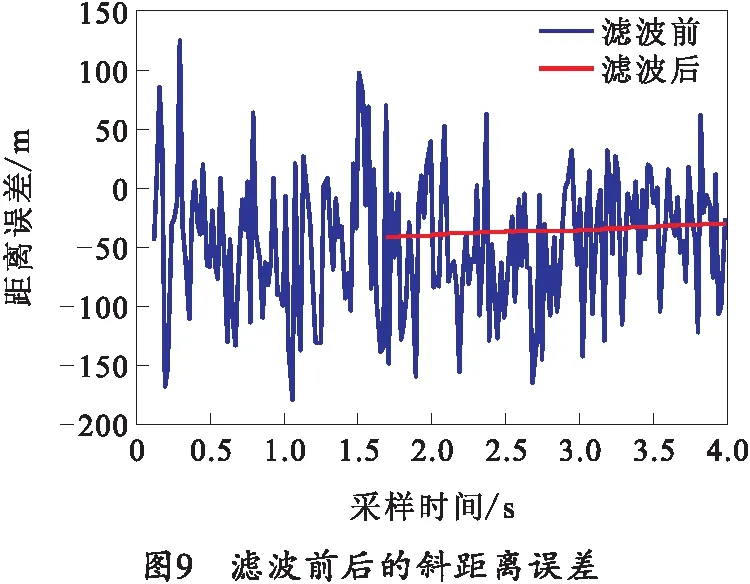
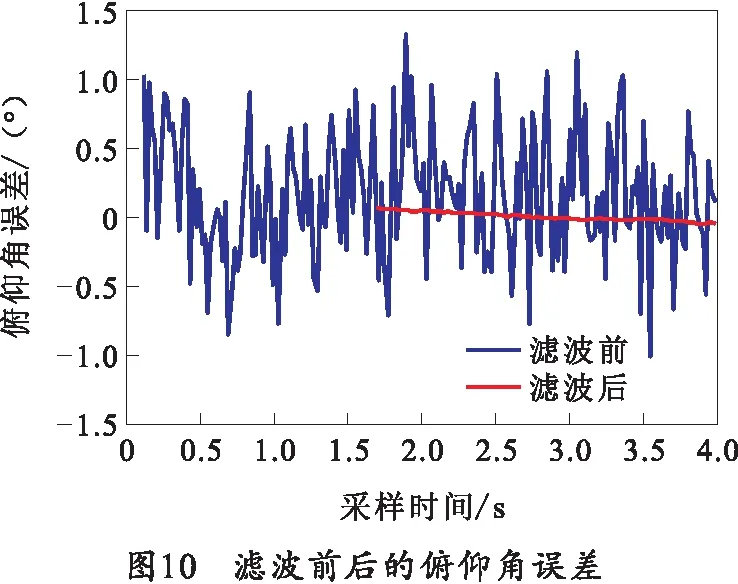

由图9~11可知,与滤波前相比,目标搜索信息从主车转换至从车后距离、俯仰角和方位角的误差在经过滤波后误差波动幅度减小,经计算可得斜距离传递误差标准差为3.173 3 m、俯仰角传递误差标准差为0.030 4°、方位角传递误差标准差为0.035 2°,满足从车转入对目标跟踪的精度需求。
6 结束语
笔者介绍了火控组网的基本原理,从建立火控组网信息传递数学模型出发,使用函数传递误差分析方法对信息共享后从车获得的目标信息的误差进行分析,对不同传感器的量测误差分别建立状态空间模型并利用卡尔曼滤波减小随机误差,最后使用滤波外推后的数据完成搜索信息的转换。仿真结果表明该方法可以减小搜索信息共享时随机误差的波动幅度,满足从车转入对目标跟踪的精度需求。
