药型罩间距对MEFP侵彻特征的影响研究
2022-04-20左亚帅张会锁王家祺李强焦军虎
左亚帅,张会锁,王家祺,李强,焦军虎
(1.中北大学 机电工程学院,山西 太原 030051;2.山西中通高技术有限责任公司,山西 太原 030600)
爆炸成型弹丸(EFP)技术是聚能破甲技术的重要分支,EFP头部质量集中,速度梯度小,开口半径大,具有对炸高不敏感、能有效对付复合装甲、后效作用良好等优点[1]。经过长时间的试验和理论研究,EFP已经具有较为成熟和完善的理论[2-4]。多弹头爆炸成型弹丸(MEFP)战斗部相比于单枚EFP增加了毁伤元数量,不仅一次可生成多个弹丸,且每个弹丸可以具有不同的飞行方向,提高毁伤效率的同时还提高了命中精度,国内外都加大了对MEFP的研究[5-7]。
常见的MEFP战斗部通常为轴对称结构,将数枚药型罩布于装药的端面或轴向[8],以及通过在药型罩前面布置不同形状的栅格,利用网栅切割形成不同数量形状的MEFP[9]。笔者主要针对端面分布式MEFP进行研究。目前对于MEFP的研究,主要集中在MEFP的成型过程,对于侵彻过程的研究较少[10-11]。由于弹头侵彻靶板时靶板内多个应力波相互干扰作用及靶板各处形变不均,MEFP装药结构所形成的弹丸的侵彻效果会受到影响,将直接影响到MEFP的侵彻深度和毁伤面积。因此为了使MEFP的侵彻深度可以得到控制,笔者采用数值模拟计算,分析相邻药型罩间距对MEFP侵彻深度的影响,对于MEFP设计具有重要的参考价值。
1 数值模型
1.1 装药结构及材料参数
选用φ60 mm球缺型变壁厚药型罩EFP战斗部,装药结构长径比N=1;药型罩采用紫铜材料,罩顶厚δ=2.1 mm、外曲率半径r1=54 mm、内曲率半径r2=58 mm。采用中心点起爆方式引爆JH-2炸药。单枚球缺型EFP装药结构如图1所示。

使用Autodyn进行数值模拟,聚能装药爆炸、药型罩翻转成型、EFP侵彻靶板等过程是多物质相互作用的过程,因此采用拉格朗日算法进行计算。拉格朗日算法是解决爆炸与冲击问题应用中最为广泛的一种方法,每个单元的顶点随填充材料一起移动,由于网格与材料一起变形,填充材料始终保持在原单元内而不会在单元之间流动[12],拉格朗日算法中很容易确定材料和结构界面以及内部应力应变状态,可以很好地模拟固体材料的动态行为[13]。模型中药型罩使用紫铜,靶板使用4340钢,炸药使用JH-2,各部分材料的状态方程、强度模型及失效模型如表1所示。其中紫铜和4340钢参数在Autodyn材料库中选取,JH-2炸药JWL状态方程参数如表2所示。

表1 材料模型

表2 JH-2炸药JWL状态方程参数
1.2 单枚EFP数值仿真模型的验证
使用图1所示EFP装药弹丸结构侵彻靶板,靶板为半无限钢靶,文献[14]中所述有利炸高为3.9~4.4倍装药直径,笔者采用直径为60 mm的装药结构,因此取炸高为240 mm,网格宽度为0.5 mm,总网格数约为350 000。图2所示为EFP到达靶板前时的形状,弹丸头部速度为2 598 m/s,采用定常流体模型对侵彻深度进行简便计算[15]:
(1)
式中:P为侵彻深度;l0为EFP的有效长度;η为EFP密实度;ρp和ρt分别为弹丸和靶板的密度。取l0为53 mm,EFP密实度η为0.85,弹丸密度ρp为8.96 g/cm3,靶板密度ρt为7.83 g/cm3,理论计算侵彻深度为52.27 mm。

数值模拟侵彻结果如图3所示,弹孔直径约为61.54 mm,侵彻深度为52.18 mm,与理论计算值吻合,且仿真结果形貌与文献[14]试验靶板剖面相吻合,证明用上文所述算法、材料模型及网格数量进行仿真所得结果是合理的。

2 药型罩间距影响分析
2.1 MEFP侵彻钢板过程分析
MEFP装药结构如图4所示,图中D为药型罩直径,d为药型罩间距,由于对MEFP整体结构进行仿真所需计算资源过大,因此将模型简化,对MEFP相邻两子装药进行仿真,能在一定程度上反映MEFP整弹的侵彻情况。

取药型罩外壁之间最短距离d=10 mm,不同时刻的侵彻过程及结果如图5所示,侵彻深度P随时间t变化曲线如图6所示,MEFP侵彻钢板过程如下:
1)从子弹丸接触靶板开始计时,5 μs前靶板中应力主要集中在弹头与靶板接触的冲击界面上,至10 μs时形成比弹径略大的弹坑。此阶段属于开坑阶段。
2)从10 μs至40 μs,应力波开始相互作用,最大应力出现在应力波交互作用区域中部,随时间增加,应力逐渐向靶板内传递。弹丸侵彻速度稳定,冲击界面附近的靶板介质在受到冲击之前,已经获得了一定的轴向和径向速度,在径向飞散的弹丸进一步作用下,弹孔直径扩大,侵彻深度增加[16]。此阶段属于侵彻的稳定阶段。
3)40 μs开始,应力分布基本稳定,应力变化主要集中于弹坑底部及两弹孔的中间区域,此时弹丸速度已经降为767 m/s左右,且速度下降很快,靶板的强度作用表现越来越明显,侵彻能力变弱,侵彻深度增加较小。由于靶板内应力波的相互作用及两弹丸中间部分靶板形变大于靶板其他位置,使得弹孔向中间倾斜。两弹孔中间的靶板强度变弱,破碎弹丸的侵蚀作用表现明显,两弹孔中间的靶板强度被进一步削弱,加大了弹孔底部的倾斜程度。
4)80 μs后,弹丸基本失去侵彻能力,弹丸在弹孔底部径向速度明显大于轴向速度,主要表现为扩孔作用,此阶段属于侵彻的终止阶段。


2.2 药型罩间距对孔径和倾斜程度的影响
炸高取240 mm,研究不同药型罩间距对MEFP侵彻钢靶弹孔形状的影响,如图7所示,随药型罩间距增加,弹孔形状发生较大改变,最明显的为弹孔倾斜程度和弹孔直径的改变。
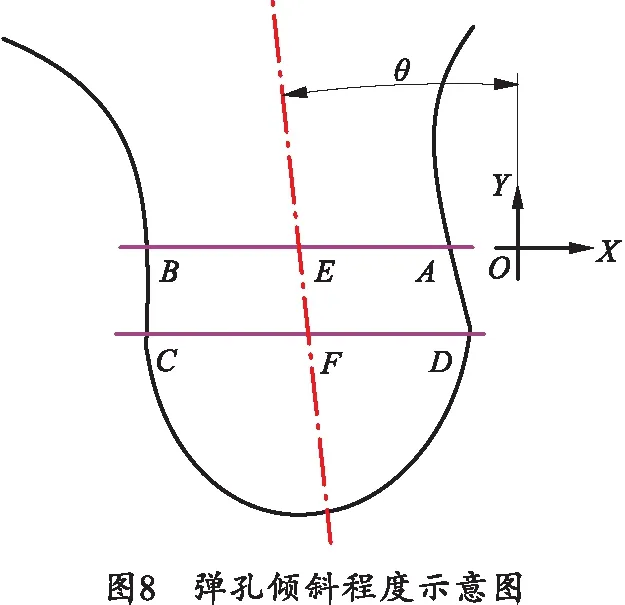
以两弹丸着靶点连线的中点为原点,建立坐标系,如图8所示,X轴与弹孔轮廓交于点A、B,作平行于X轴的直线过弹孔轮廓上X最大值点D,与另一侧轮廓交于点C,取直线AB中点E和直线CD中点F,直线EF与Y轴夹角θ即为弹孔倾斜角度,AB的距离即为弹孔直径φ。

以两弹丸着靶点连线的中点为原点,不同药型罩间距下弹孔轮廓如图9所示,随药型罩间距的增加,弹丸间相互作用减弱,靶板内冲击波交互作用时间延后,两弹中间靶板形变程度与其他部位靶板形变程度逐渐接近,弹孔倾斜角度逐渐变小,弹孔直径有所增加;当药型罩间距等于药型罩直径时,弹孔倾斜角度约为3.8°,弹孔直径约为单枚EFP弹孔直径的93.3%,具体数据如表3所示,表中d为相邻药型罩外壁最小间距,D为药型罩直径,θ为弹孔倾斜角度,φ为弹孔直径。
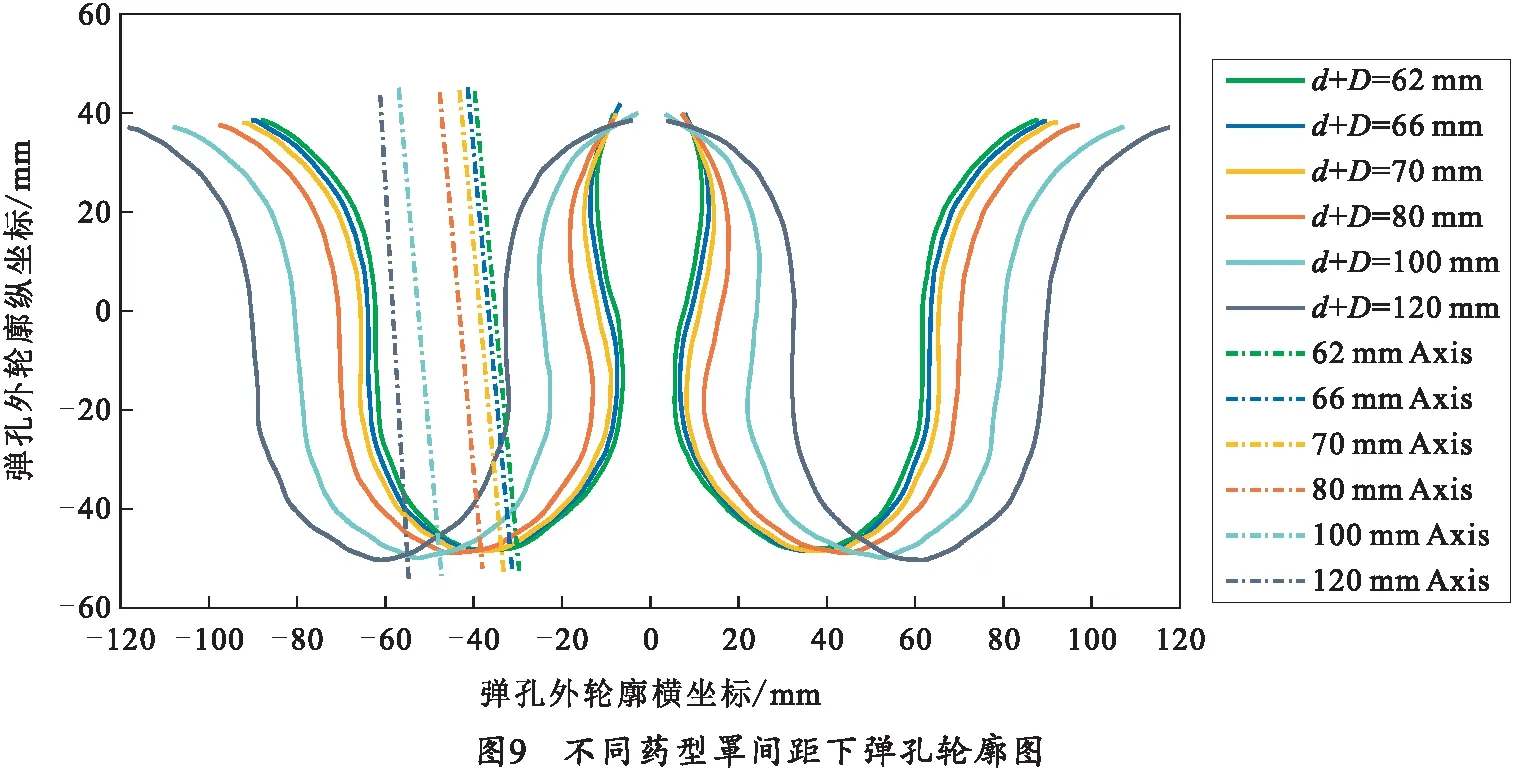

表3 弹孔倾斜角度与弹孔直径
药型罩间距与弹孔倾斜角度及弹孔直径之间的关系如图10所示。

药型罩间距与弹孔倾斜程度和弹孔直径之间呈现明显的正相关,说明随药型罩间距的增大,弹孔倾斜角度变小,弹丸具有更多的剩余能量用于扩孔。当药型罩间距大于1.2倍单枚弹径后,弹孔基本不倾斜,孔径增加变缓。
2.3 药型罩间距对侵彻深度的影响
如图11所示,以两弹着靶点连线的中点为坐标原点,建立坐标系,X轴与弹孔轮廓交于点A、B,作平行于AB的直线,与弹孔底部相切于点G,该直线与X轴的距离即为垂直侵彻深度P1,作平行于弹孔中心线的直线,过点G与直线AB交于点K,KG之间的距离即为最大侵彻深度P2,因此,最大侵彻深度与垂直侵彻深度之间的关系为
P2=P1cosθ.
(2)

两弹丸时,垂直侵彻深度具体数据如表4所示,最大侵彻深度具体数据如表5所示。

表4 两弹丸垂直侵彻深度

表5 两弹丸最大侵彻深度
药型罩间距d大于药型罩直径D后,侵彻深度增加变缓,最大侵彻深度和弹孔形状与单枚EFP侵彻效果接近。
药型罩间距与侵彻深度之间的关系如图12所示,其中局部放大图为药型罩间距小于单枚弹径时侵彻深度散点图,发现当药型罩间距小于单枚弹径时,药型罩间距与侵彻深度表现为明显正相关的线性关系。

对垂直侵彻深度12个散点进行线性拟合,自由度为10。采用y=a+bx进行拟合,其中y=P1/D,x=d/D,当a=0.803 49时标准差为3.735 48×10-4,当b=0.033 61时标准差为7.989 5×10-4,经过整理得到垂直侵彻深度P1为
P1=0.803 5D+0.033 61d.
(3)
对最大侵彻深度6个散点进行线性拟合,自由度为4。采用y=a+bx进行拟合,其中y=P2/D,x=d/D,当a=0.808 15时标准差为3.909×10-4;当b=0.031 4时标准差为7.583×10-4,经过整理得到最大侵彻P2为
P2=0.808 2D+0.031 4d.
(4)
式(3)和式(4)所拟合直线的残差平方和分别为7.878×10-6和1.640 3×10-6,残差平方和越小表明拟合程度越好。Pearson相关系数分别为0.997 2和0.998 8,表明药型罩间距与侵彻深度之间表现为极强正相关。可决系数R2分别为0.993 8和0.997 1,表明拟合优度好,回归直线对观测值的拟合程度高,因此,所拟合直线能够准确反映药型罩间距和侵彻深度之间的关系。
综上所述,随药型罩间距的增加,侵彻深度逐渐增加,最大侵彻深度相较于垂直侵彻深度,虽增长速度有所减缓,但差别不大;并且随药型罩间距增加,侵彻所形成的弹孔倾斜程度逐渐减小,弹孔直径逐渐增加。说明当药型罩间距过小时,弹丸能量主要消耗在弹丸之间的相互作用,及弹丸对两弹中部靶板的横向侵彻和挤压。当药型罩间距d大于药型罩直径D后,弹丸之间的相互影响基本可以忽略不计,且两弹中间靶板形变程度与其他部位靶板形变程度逐渐持平,MEFP的最大侵彻深度达到单枚EFP侵彻深度的96.6%,认为药型罩间距大于药型罩直径后,侵彻深度受到的影响迅速减少。
3 结论
1)对MEFP进行数值模拟,发现侵彻后所形成的弹孔向中间倾斜。随药型罩间距的增加,倾斜角度逐渐减小,弹孔直径逐渐增大;当药型罩间距等于药型罩直径时,弹孔基本不发生倾斜,倾斜角度约为3.8°。当药型罩间距大于1.2倍药型罩直径后,弹孔倾斜程度和孔径所受到的影响迅速减小。
2)对两弹丸侵彻过程进行分析,发现随药型罩间距增加,最大侵彻深度逐渐增加,由0.81倍弹径增加至0.858倍弹径;同时弹孔倾斜程度减少,倾斜角度由6°逐渐垂直;弹孔直径逐渐增加,由0.9倍弹径上升为0.99倍弹径;说明药型罩间距过小时,部分能量消耗与弹丸间的相互作用及对弹孔底部的径向侵蚀,这部分能量大于开孔所需能量。
3)当药型罩间距大于弹径后,MEFP最大侵彻深度达到单枚EFP侵彻深度的96.6%,随药型罩间距进一步增加,MEFP最大侵彻深度逐渐与单枚EFP侵彻深度接近,弹孔形状与单枚EFP相吻合;药型罩间距小于弹径时,药型罩间距与侵彻深度之间表现为明显的正相关线性关系。因此对于MEFP设计来说,在几何尺寸条件允许的情况下,应尽可能加大药型罩间距,减少能量消耗和弹丸间相互作用,在提高侵彻深度的同时,增大毁伤面积,本研究对于MEFP战斗部研制具有一定的参考价值。
