高炮反无人机目标分配建模及优化算法研究

张驰，张春

(西北机电工程研究所，陕西 咸阳 712099)

近年来固定翼和旋翼小型战术无人机快速发展，基于小型无人机的集群式攻击已成为现役防空系统面临的主要威胁之一[1]。无人机蜂群会给防空体系带来巨大压力，同时也将严重威胁防空部队自身安全[2]。2020年9月27日，亚美尼亚同阿塞拜疆爆发了激烈的军事冲突。在冲突中，阿方军队大量利用无人机对亚美尼亚军事设施和人员进行了“降维式打击”，战况在互联网上迅速传播，为这场军事冲突打上了鲜明的时代烙印[3]。

目前对无人机的拦截主要包括软、硬毁伤两种形式，软毁伤主要以诱骗干扰、激光烧蚀、微波毁伤等形式对无人机进行打击；硬毁伤主要以高炮、导弹等动能杀伤形式对目标进行打击。现有的反无人机系统在其环境适用性与作战效能方面有一定的作战局限性，在复杂多变的战场环境下，难以有效应对成体系、多批次的蜂群无人机的攻击。采用硬毁伤的方式打击无人机蜂群，特别是通过高炮发射预制破片弹药的形式进行拦截，可在无人机目标区瞬间形成大量密集弹幕，对无人机、蜂群无人机可形成较大覆盖范围的毁伤[4]。

1 防空反无人机战场态势分析

作战指挥需要在感知双方装备状态的基础上，熟悉战场环境，采取有效的动态求解策略[5]。因此，对战场态势的理解、估计和预测已成为战场信息优势研究的重点[6]。

在实际的战场情况下，需要由指挥员根据我方和敌方的战场态势，综合考虑制定我方的打击方式。依据毁伤数据库预测能力，有效获取战场态势，了解敌我双方装备状态，是实施打击策略制定的前提条件[7]。在获取战场态势的前提下，通过优化方法进行评估，从而得到最优打击策略，并用于指导战场作战，是毁伤评估体系建立发展的最终目标。

不同的打击策略，对应的毁伤效能也不同。对于某一特定目标，采取哪种打击，不同工况的各个特征数据作为优化方法的自变量，通过优化方法来寻优，在一定范围内得到最优值，得到最优打击策略。对打击策略进行进一步推广，当战场存在多个打击目标的情况下，也可以在多个目标之间进行优化迭代，根据毁伤评估体系与优化策略，得到最优打击决策，如图1所示。

2 反无人机的目标分配模型分析

防空目标分配是防空指挥控制中最为重要的环节之一，也是决定作战效能的关键因素之一[8]。防空目标分配的目的就是将来袭无人机合理科学地分配给各防空系统火力单元，使防空火力系统可以最大化作战效能[9]。其分配过程是通过信息处理、威胁判断、数据融合，形成综合战场态势，从而实现目标分配和战场指挥。

2.1 无人机目标威胁指标评估

防空目标威胁分析是多因子决策问题，需要考虑的因素较多。通常情况下，主要考虑以下因素：保卫目标的位置和重要性；空袭目标的类型、架数、高度、速度、来袭方向；空袭目标到保卫目标的距离、航路捷径等。取A=[a1,a2,…,aj]为无人机目标方案集，U=[u1,u2,…,um]为评估指标集[10]。无人机目标aj按照评估指标um来进行测度，可得到目标威胁的决策矩阵，由该矩阵进而可以得到目标无人机的威胁矩阵[w1,w2,…,wj]。

2.2 射击转火周期

转火射击是高炮在对进入防区的某一无人机射击完成之后，按照指示调转炮口，对其他无人机进行射击的一种方法[11]。从本次火控计算机收到射击命令，经转火后到下次火控计算机收到射击命令的时间间隔，称为转火射击周期tzh，转火射击周期取决于本次射击时间tsj和转火的准备时间tzb，射击时间tsj是从火控计算机接收射击命令至炮弹与目标无人机在空中相遇并监测其毁伤效果的时间，在本文中为固定值，为

tsj=tfs+(n-1)t1s+tpg,

(1)

式中：tfs为从火控计算机接收射击命令到炮弹出膛所需的时间，其为固定值；tls为一次连射多发炮弹所需的时间间隔总和；tpg为炮弹的飞行时间和毁伤效果评估时间。

在单次射击结束后，组织转火射击的准备时间tzb为炮手下达转火命令所需时间和炮口调转所需要的时间之和，通常情况下，组织转火射击的准备时间tzb为3 s。高炮最终的转火周期为

tzh=tfs+(n-1)t1s+tpg+tzb.

(2)

2.3 防空火力分配区域

在高炮抗击蜂群无人机的作战过程中，准确地把握目标分配的时机尤为重要，既不能过早分配指示，以防止目标机动给目前的分配方案加大计算量；也不能指示过晚，导致高炮毁伤效能下降。防空高炮的火力区域划分是指在进行防空作战目标分配时，使所分配的目标和炮弹在火力杀伤区相遇的空间区域。

火力分配的区域远界为

ρyj=

(3)

火力分配的区域近界为

ρjj=

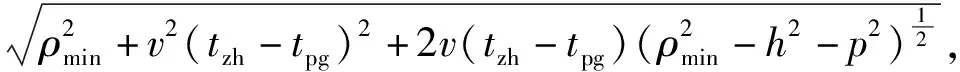
(4)

式中：ρmax、ρmin分别为高炮毁伤区域的远界和近界；h、p分别为来袭无人机的来袭高度和来袭航路捷径。

2.4 对无人机毁歼概率的计算方法

高炮武器系统的毁歼概率的计算方法为命中概率Pmz与命中条件下击毁目标概率Pjh的乘积，即：

P=PmzPjh.

(5)

严格地说，命中概率和击毁概率并不相互独立，因为毁歼概率不仅以命中目标为条件，而且与弹丸命中目标的部位等因素有关。但一般工程应用中，为了使问题不至于过于复杂，计算毁歼概率一般都认为命中概率与平均毁歼概率相互独立。

对毁伤目标的规律进行如下假设：每门高炮命中目标后毁伤目标的事件是相互独立的，命中弹毁伤目标的概率记为pi=1,2,…,m，在此假定下，多门高炮抗击目标的概率G(K)：

(6)

2.5 模型建立

在防空作战中，防空优化火力分配遵循的主要原则是:优先选择毁伤概率高且威胁度指数高的火力单元进行拦截，同时兼顾火力资源的消耗情况[12]。现有简化模型如下所示。

假设现有m门高炮，n为同一批次来袭无人机目标的个数，wj为第j个无人机目标的威胁度，pij为第i门的高炮对无人机目标j的毁歼概率，xij为第i种武器分配给目标j的决策变量(1表示分配，0表示不分配)，对无人机目标的毁歼概率为

(7)

分配结果的分配效能为

(8)

在实际情况下分配结果除了需要满足将敌方目标对我方的威胁减至最低之外，还需要在达到相当打击效果下使用尽可能少的武器消耗，也即武器使用有其相应的代价，不能毫无节制的滥用。B(x)作为分配结果的分配效能，是一个极值问题，应通过某一参数的调节，使得当武器分配消耗增加到一定程度时，毁伤效果提高不明显。因此，在上述建立的公式基础上，为实现消除目标威胁、毁伤概率和武器使用代价的平衡，构建了如下的目标函数：

(9)

式中，μ(Pi)为满意度函数，规定μ(Pi)是以理想的毁伤概率为其函数值波峰位置的函数，毁伤概率未达到预设的理想概率时，满意度随着毁伤概率的增加缓慢增加；毁伤概率超过预设的满意程度时，满意度随着毁伤概率的增加而快速下降。

转火目标数量限制：

因为自营的地区覆盖很难，而这种模式是将第三方与自营两者整合起来，这样一来就能够大大的提升送货的效率、也可以找到合作人共同承担前期的投入成本，如人力、冷冻车等。例如：某公司现在在用的冰袋加保温箱的配置来打包产品，再交由第三方去送，公司只负责打包和全程监督管理。

(10)

单架无人机占用高炮的数量约束：

(11)

转火时间条件数学描述如下：

(12)

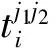
3 算法设计及仿真分析

针对目标分配问题和优化策略，采用混合智能优化算法进行仿真。目标分配模型具有非线性约束，不能用消元法将其转化为无约束问题。为了解决这一问题，笔者采用罚函数将其转化为无约束优化问题,同时将离散粒子群算法引入模拟退火思想来求解目标分配问题，以提高算法对全局最优解的搜索效率。

3.1 改进离散粒子群优化算法

离散粒子群优化算法(DPSO)是Kennedy和Eberhart于1997年提出的粒子群优化算法的离散版本，算法将离散问题空间映射到连续粒子运动空间，并对粒子群优化算法进行适当的修改求解，在运算方式上仍保留经典PSO算法的迭代运算规则[13]。粒子在状态空间的取值和变化只限于0和1之间，而速度的每一维代表位置每一维xij取值为1的可能性。

DPSO算法的优势在于充分利用连续粒子群算法计算简单快捷的优点，但还是存在连续粒子群算法容易陷入局部最优的缺点。针对上述不足，将模拟退火思想引入到DPSO中，利用模拟退火算法在一定概率控制下暂时接受一些次优解的特点，对基本的DPSO算法进行改进，围绕初始解进行模拟退火优化，以此达到在小范围内的细致搜索，避免早熟和增强算法收敛的目的。

基于模拟退火改进的离散粒子群算法(SA-DPSO算法)是双层的并行结构。该算法把离散粒子群算法所获得的优化结果作为模拟退火算法的初始种群；同时将通过metropolis抽样得到的模拟退火算法的解作为下一轮优化的初始种群。基于此，笔者将SA算法和DPSO算法相结合来求解火力分配问题。在保证一定的优化质量的前提下，依次进行优化，提高优化效率。SA-DPSO混合优化算法的具体流程及流程图如图2所示。

步骤1初始化参数。确定惯性权重ω，学习因子c1、c2和群体规模R，设定最大迭代次数为kmax，随机产生R个粒子的种群。

步骤2计算每个粒子的适应值Gr，将其适应值Gr与个体极值pbest进行比较，取优更新为个体极值pbest。

步骤3将其个体极值pbest与全局极值gbest进行比较，取优更新为全局极值gbest。

步骤4如果满足终止条件，则结束程序，否则，执行步骤5。

步骤5执行SA算法。

1)初始化SA参数，设定初始温度T和每个T值的迭代次数L；

2)对k=1,2,…,L执行步骤3～步骤5；

3)产生新解x′r，计算Δf=Gr-Gr′，其中Gr′为新解的适应度函数；

4)若Δf<0，则接受x′r，xr(k+1)r=x′r，否则以概率exp(-Δf/T)接受x′r，xr(k+1)r=x′r；

5)如果满足终止条件，则输出当前解作为最优解，结束程序。

步骤6以退火温度收敛率α逐步降低温度，即T(k+1)=λT(k)，如果T≥0，转步骤2，否则结束程序。

3.2 仿真及结果分析

为验证笔者提出的目标分配模型的科学有效性，以及SA-DPSO混合优化算法求解目标分配问题的寻优能力和收敛性，针对实例进行仿真：9架S-70无人机依次入侵防区，6门不同位置的高炮，高炮对等速直线运动目标实施一次点射。9架无人机对保护目标的威胁指标因子和每门高炮火力毁伤无人机的概率如表1所示。

表1 无人机威胁度及毁伤概率

各无人机的飞临时间(s)为

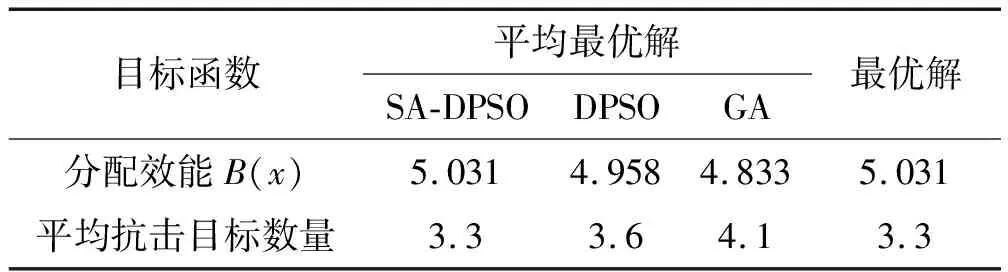
采用笔者提出的防空火力分配模型进行目标优化分配，转火时间取平均值4 s，并且采用SA-DPSO算法对该目标分配问题进行求解，其中惯性系数逐渐由1.1线性递减至0.4，学习因子为1.5，初始化种群粒子为100，初始化温度设为10 000，温度冷却系数为0.9，每个粒子代表一种目标分配的方案，当Pi≤0.9时,Pi=log1.9(Pi+1),当0.9

可以看出，笔者所提出的反无人机目标分配模型可以实现满足转火时间限制条件下的目标分配规划，对每个目标的联合毁伤概率可达到

P=[84.87% 95.80% 94.20% 93.99% 96.80% 96.80% 92.05% 92.52% 94.80% 91.00%].

为了验证笔者提出的SA-DPSO算法的性能，对提出的目标分配模型采用经典DPSO算法和经典遗传算法(GA算法)进行了20次的仿真，其中GA算法初始种群数目为50，染色体二进制编码长度为20，最大进化代数为100，价差概率为0.8，变异概率为0.1，每个粒子代表一种目标分配方案，进行仿真直至对每一架无人机的毁歼概率都不低于90%为止，各算法的分配结果及最优分配的适应值变化如图3和表2所示。

表2 3种算法的平均最优解

表2显示，最优解通过SA-DPSO算法解得，表明SA-DPSO算法有更好的寻优能力，相比于GA算法和DPSO算法，SA-DPSO算法的单门高炮平均抗击目标数分别减少了9.1%和24%，即在对每一架无人机的毁歼概率都不低于90%的仿真测试中，也通过SA-DPSO算法分配的高炮系统的作战压力最小。图3显示3种算法的迭代次数，SA-DPSO算法收敛的最快且收敛性最好。通过对比可得，笔者提出的SA-DPSO算法是快速且可靠的。

4 结束语

防空反无人机目标分配问题一直是军事科技领域竞相研究的前沿热点问题，这不仅关系到战场上指挥员做决策，而且对武器装备的论证研制和运用有着不可替代的作用。笔者提出一种多指标因子的抗击蜂群无人机的目标分配模型，引入了威胁度指标、高炮转火时机和高炮实际火力分配区域，加入了对目标无人机转火的时间限制，优化了最终的目标函数，建立了完善的高炮抗击蜂群无人机的目标分配评估的指标体系。在此基础上，对离散粒子群算法引入模拟退火的思想，通过对实例进行分析，获得了对高炮抗击无人机蜂群较好的目标分配方案。仿真结果表明，所提出的反无人机目标分配模型是合理且科学可靠的；SA-DPSO算法能够有效的提高对最优解的寻优能力，该研究成果可为工程应用提供参考借鉴。