思维导图在数学证明中的应用

王霁香

摘要：随着“双减”政策的推进落地。学校要减轻学生学业负担，提高课堂教学质量。数学作为培养学生抽象思维和推理能力的基础学科。本着人人都能获得良好的数学教育，不同的人在数学上得到不同发展的培养目标。在数学证明中引用思维导图教学方式，对提高数学课堂质量起到重要作用。

关键词：思维导图;推理能力培养;课堂质量

国家开展“双减”工作，坚持以习近平新时代中国特色社会主义思想为指导，着眼建设高质量教育体系，提升学校教育教学质量，提高课堂教学质量。如何减轻学生学业负担，是每一位教师应担当的责任，如何减轻学生思维负担，是每一位教师应探索的思考，如何减轻学习过程负担，是每一位教师应转变的方式。

作为一名数学教师，在“双减”浪潮中激荡，努力追赶潮流。始终怀着培养学生抽象思维和推理能力的初心，在数学证明中不断尝试，不断修正、不断创新。努力完成人人都能获得良好的数学教育，不同的人在数学上得到不同的发展的培养目标。

在北师版《数学课程标准》中，要求知道证明要合乎逻辑，知道证明的过程可以有不同的表达形式，会综合法证明的格式。我以《义务教育教科书·数学》（八年级上册）第七章平行线的证明学习为载体。引入思维导图教学方式，提高课堂教学质量。让学生体会演绎推理的严谨性，让学生树立步步有据的推理意识，让学生发展推理能力，让学生掌握综合法证明的格式。例如：书177页知识技能2题。已知：如图，AD∥BC ，∠ABD =∠D ，求证：BD 平分∠ABC.

分析：要证明BD 平分∠ABC  ，

只需证明∠ABD = ∠DBC

因为∠ABD =∠D ，所以只需证明∠D =∠DBC

又因为AD∥BC ，所以依据“两直线平行，内错角相等”即可证明.

综合法证明，步步有据：

∵AD∥BC （已知）

∴∠D =∠DBC （两直线平行，内错角相等）.

又∵∠ABD =∠D （已知），

∴∠ABD = ∠DBC （等量代换）.

∴BD 平分∠ABC （角平分线的定义）.

思维导图的绘制，减轻学生思维负担。在解决问题的过程中，推理能力的发展贯穿于整个数学学习过程中。

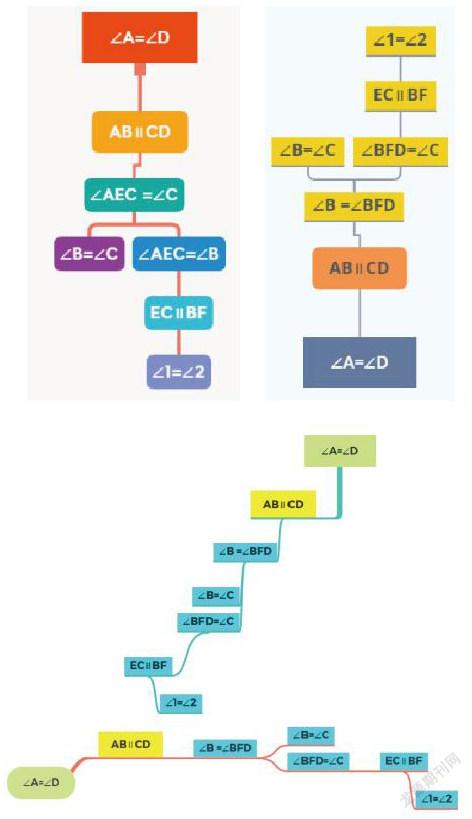
再如：书177页数学理解4题。如图，一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A，G，H，D，且∠1 =∠2 ， ∠B =∠C.求证：∠A =∠D.

思维导图的呈现，减轻学生过程负担，对于命题的证明，合情推理用于探索思路，发现结论。演绎推理用于证明结论。构建思维导图的实践操作活动，激励学生积极思考。将解题思路以图形形式呈现出来，减轻学生厌烦情绪。多种思路和方法在全体学生中交流展示，张扬学生探知个性，激发学生学习兴趣。在寻求证明思路的过程中，可以从已知向求证探索;也可以倒过来从求证向已知追溯;還可以从已知和求证两个方向分别出发，互相接近。证明思路的发现，证明格式的规范、语言表达的简洁，课堂质量得以保证，学生有效参与得以促进，课堂学习效益得以提高。

数学不仅是数与形的研究，更是一种思维方式，是演绎推理和归纳推理的逻辑思维方式。教学证明过程中借助思维导图，不仅能够帮助学生更好地梳理知识的生成过程，而且能够更好地完成知识的逻辑关系和结果表达，进而有效地促进数学课堂教学质量的提升。

“双减”政策下，我们不仅要授人以鱼，而且要授人以渔。学会思考，发现和提出问题，分析和解决问题，有意义的学习、合作学习和创造性学习，最终学会学习，才是我们每位老师要研究的事情，路漫漫其修远兮，吾将上下而求索。