双层柱面网壳受力分析研究

白文阳

摘 要：双层柱面网壳的建模计算及优化分析是本研究的主要内容。本研究所建模型腹杆的连接方式有抽空正放四角锥体系与正放四角锥体系两种形式。在参数化建模的基础上，通过ANSYS有限元静力分析，得到了两种形式下的双层柱面网壳结构应力、杆件内力值以及位移，并对其结果进行分析，总结出其中相对应的规律。在对结构静力分析结果的基础上，对正放抽空四角锥体系双层柱面网壳结构的杆件进行截面优化，运用相对应的截面优化方法（通过不断改变截面面积）找到该种网壳结构形式下的最优截面，直到得出使结构总重量最小但结构能够满足安全要求时的结构形式。

关键词：双层柱面网壳;四角锥;截面优化;计算模拟;参数化建模

中图分类号：U448     文献标志码：A     文章编号：1003-5168（2022）5-0073-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2022.05.016

Force Analysis and Study of Quadrangular Pyramid Double-layer

BAI  Wenyang

（Beijing Xinqiao Technology Development Co.， Ltd.， Beijing 100000，China）

Abstract： The modeling calculation and optimization analysis of the double-layer cylindrical reticulated shell are the main content of this study. The connection mode of the web rods of the model built in this study has two forms： the evacuated positive quadrangular pyramid system and the positive quadrangular pyramid system. On the basis of parametric modeling， through ANSYS finite element static analysis， the two forms of double-layer cylindrical reticulated shell structure stress， member internal force value and displacement are obtained， and the results are analyzed， and the corresponding ones are summarized. Based on the results of the static analysis of the structure， the cross-section optimization of the double-layer cylindrical reticulated shell structure of the evacuated quadrangular pyramid system is carried out， and the corresponding cross-section optimization method is used （by continuously changing the cross-sectional area of the cross-section） Find the optimal cross-section under this kind of reticulated shell structure until the structure that minimizes the total weight of the structure but the structure can meet the safety requirements is obtained.

Keywords： double-layer cylindrical reticulated shell;quadrangular pyramid;section optimization;calculation simulation;parametric modeling

0 引言

網壳结构的使用非常广泛，在日常生活中，也能经常见到网壳结构。例如，火车站站台的顶棚、人行桥上部顶棚、停车处的车棚顶等都采用的是网壳结构。

1 网壳结构的特点与优点

第一，网壳结构不同于网架，它是一个弧面，就像是一个拱桥，在承受荷载方面要远远优于平面网架，其通过杆件连接而成，自重较轻、杆件内力形式单一、受力合理，是网架与壳体的完美结合。

第二，网壳结构本身拥有较大的整体刚度，可以满足大跨度空间钢结构的需求。一般100 m以上的大跨度会因为平面网架结构的刚度不足、稳定性不够而不适用，但是网壳结构却不同。

第三，网壳结构是通过各种基本杆件、连接处的钢节点和一些小的部件（如套筒）安装拼接而成的。而这些部件可以通过计算得到型号与尺寸后在工厂预制好所有的部件而不需要在工地进行现场加工，这样既节省了施工周期也节约了成本。

第四，网壳结构的构造形式比较简单，通过节点将杆件以一定的方式连接成为一个整体。利用计算机软件建筑网壳模型，分析起来更便利。

第五，在空间结构发展的过程中，网壳结构也在不断地更新，特别是形式的变化层出不穷，所以网壳结构可以适应各种场合，设计者可以通过不同的建筑环境来设计出不同的网壳形式，充分展现网壳形式的美感。

2 主要研究内容

首先，对柱面网壳的各种结构形式做一些简单的介绍，并总结一些柱面网壳在设计过程中需要注意和遵守的相关规范，结合实际初步确定所要研究的柱面网壳的形状尺寸与结构形式。其次，对两种双层柱面网壳进行静力分析，在相同的柱面形式和条件下，通过对各种工况下杆件内应力值的大小以及结构在受力状态下的位移值的比较，分析对结构的不利工况，并讨论抽空正放四角锥体系与正放四角锥体系的不同，通过应力值找出网壳内杆件内力的分布规律，在应力云图得到最危险杆件的位置，最后得出相对应的结论。最后，在前面研究完成的基础上，网壳结构形式保持不变，同时要在满足强度、刚度以及稳定性的前提下，通过不断改变网壳杆件的截面面积，对正放抽空四角锥双层柱面网壳的杆件截面进行优化。

3 柱面网壳结构选型与设计

3.1 柱面网壳结构形式

柱面网壳是曲面空间结构的其中一种结构形式，分为单层柱面网壳与双层柱面网壳，而单层柱面网壳与双层柱面网壳又可以分为许多不同的结构形式。每种结构形式都有其独特的受力特点，这也为本设计提供了更多的选择。

双层柱面网壳不仅仅可以改变上下两层柱面网壳的结构形式，还可以通过不同的腹杆连接方式来改变上下层之间不同的连接形式，这就使得双层柱面网壳的结构形式远远要比单层柱面网壳的结构形式更多更复杂。下面主要讨论腹杆不同的连接形式对双层柱面网壳的影响。腹杆的连接方式是多种多样的，有的腹杆基本单元是角锥体系，而有的是交叉桁架体系。本研究初选的是抽空正放四角锥体系与正放四角锥体系。

3.2 柱面网壳结构设计

柱面网壳并非随意设计，为了保证结构的稳定性及安全性，在设计时必须遵守网壳结构技术规程中的相关规定，其中包括网壳的矢跨比、厚跨比、网格数和网格尺寸、受力特性、杆件与节点的设计等。网壳结构除了竖向反力外，通常还有比较大的水平反力，所以在施加约束时要施加全约束，防止网壳被压扁。

本次设计初选双层抽空正放四角锥柱面网壳与正放四角锥双层柱面网壳。杆件受力合理，上下弦杆的长度相差不大，空间刚度较好而且构造简单。

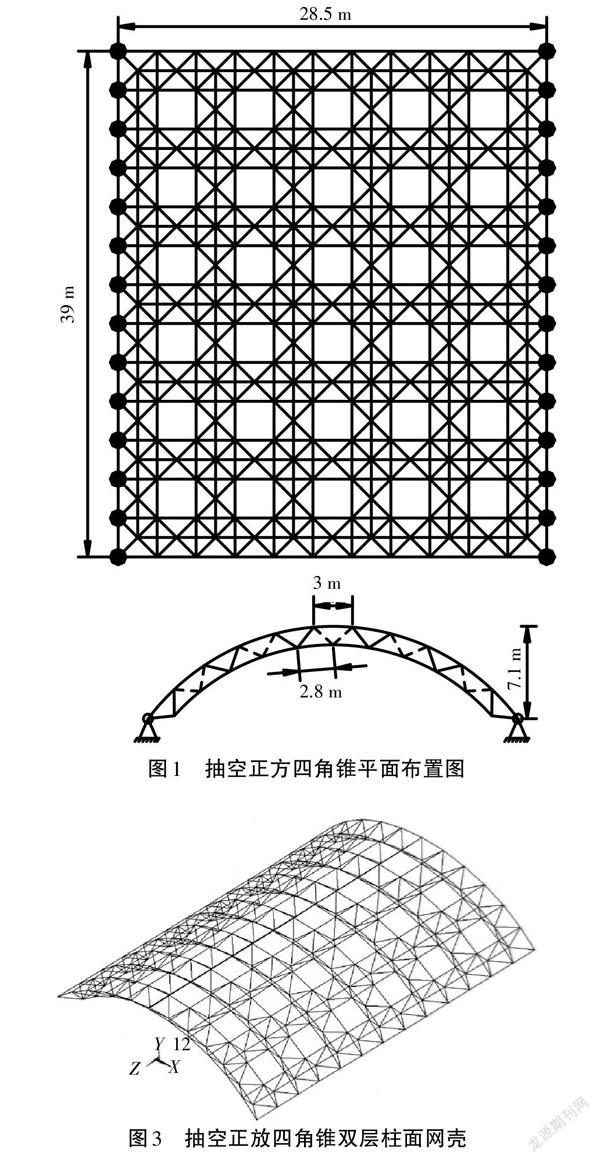
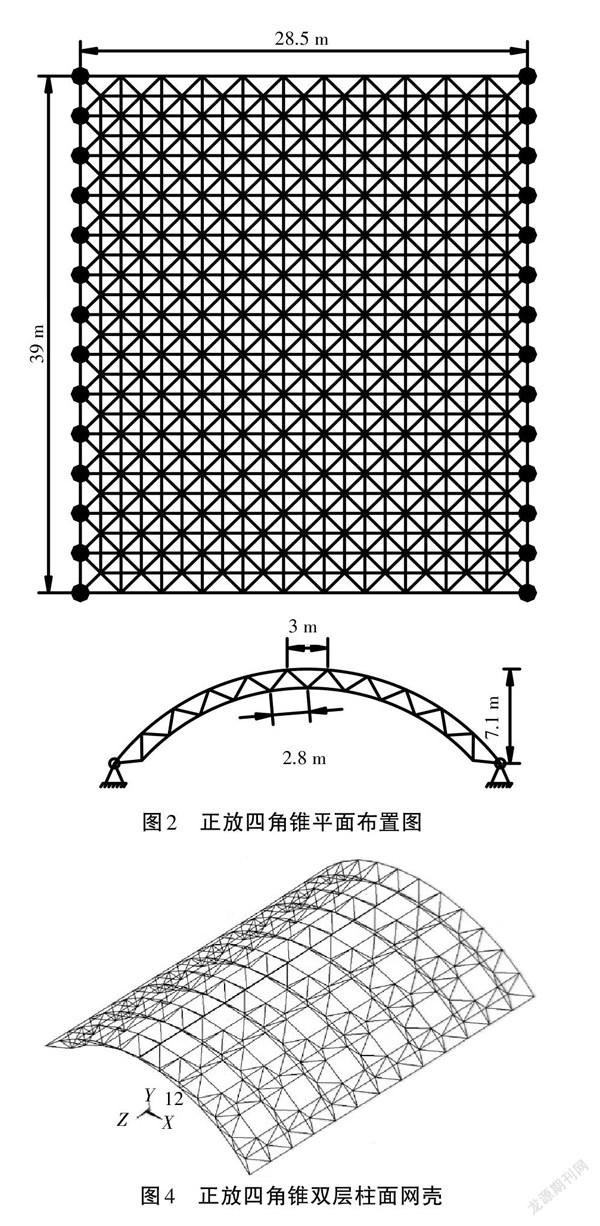
根据规范[1]，网壳的矢跨比可取1/6～1/3，网壳在短边方向的网格数不能低于6。设计中网壳的上层在短边方向跨度为28.5 m，长边方向跨度为39 m，矢跨比为1/4，厚跨比为1/20，选用的是3 m×3 m的网格，短边方向为11个网格，长边方向为13个网格;下层在短边方向跨度为24.4 m，长边方向跨度为36 m，选用的是2.8 m×3 m的网格，短边方向为10个网格，长边方向为12个网格;腹杆长度为2.6 m。网壳的平面布置图如图1、图2所示。

4 柱面网壳有限元数值分析

4.1 有限元模型的建立

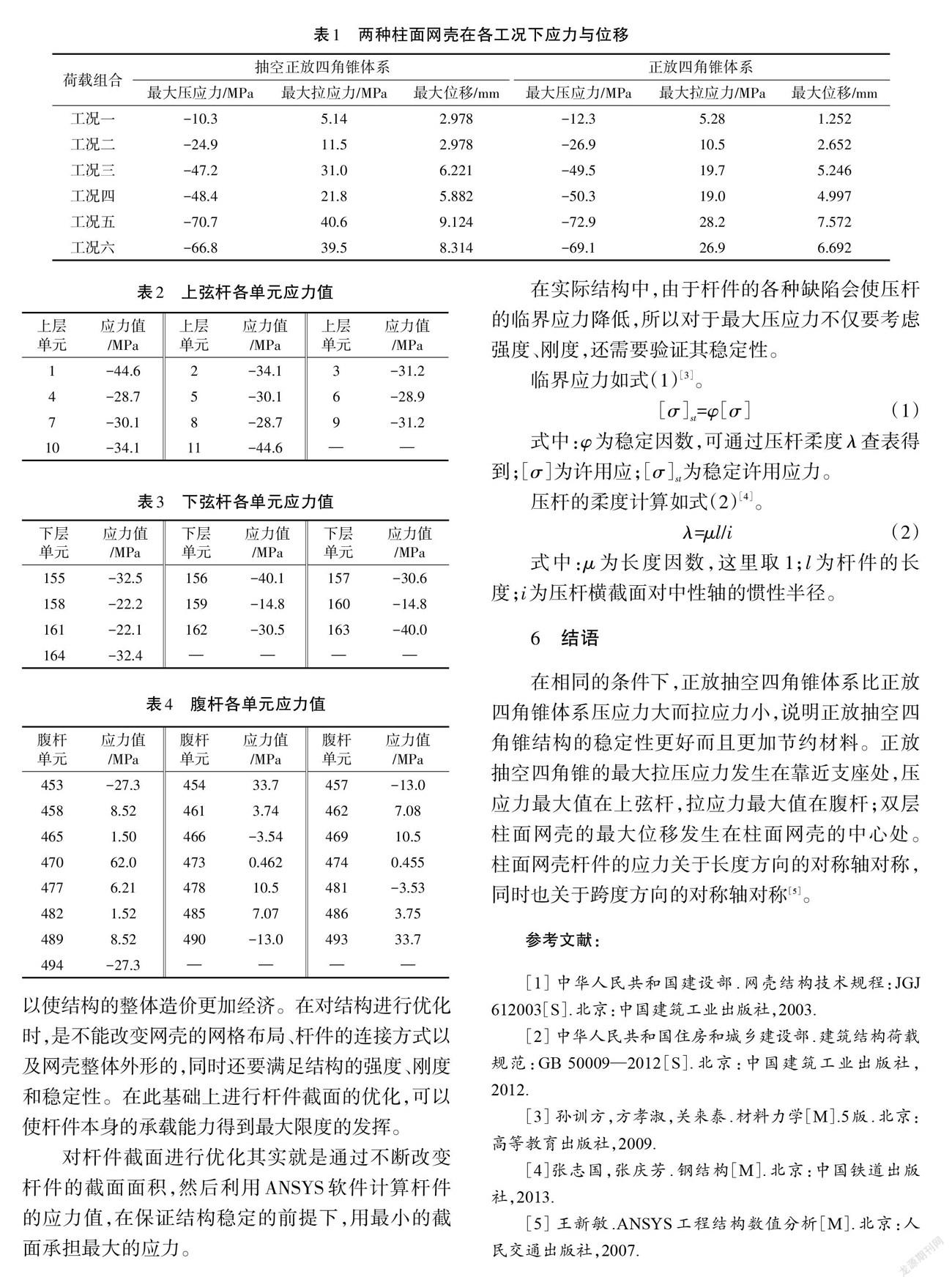
目前，空间杆单元与空间梁单元是网壳结构有限元分析计算时最常用的单元类型，双层柱面网壳结构在进行有限元分析计算时应该采用空间杆单元。笔者主要研究的是柱面网壳的变形情况以及杆件的内力、应力的分布情况，选择大型有限元通用软件ANSYS最合适。在运用ANSYS对双层柱面网壳进行静力分析的时候，网壳中的杆件选用Link8单元，钢材的密度为7 850 kg/m3，钢材的弹性模量为2.06×1011 N/m2，泊松比为0.3，网壳中杆件一律使用无缝热轧钢管。将各种工况下的均布力通过面积等效分配到各个节点上变为集中力[2]。模型如图3、图4所示。

4.2 不同工况下两种柱面网壳的应力、位移的对比

在荷载与杆件相同的情况下，正放抽空四角锥体系比正放四角锥体系的压应力大而拉应力小，且正放抽空四角锥体系的最大位移比正放四角锥体系的大。这是因为抽空四角锥体系的用料少，自重轻，所以应力值更加安全。这样节省成本且能满足受力要求，如果在没有位移的限制時，可以尽量选用抽空四角锥体系。表1为抽空正放四角锥体系与正放四角锥体系在不同工况下的静力分析结果。

4.3 不利工况下抽空四角锥柱面网壳的应力分析

抽空四角锥柱面网壳在跨度方向上不同杆件在最不利工况下的应力值如表2、表3、表4所示（杆件的方向为从左到右，最左端与最右端是靠近支座的杆件）。

由表2、表3、表4可知，上弦杆与下弦杆都是受压的，而且上弦杆靠近支座处的压应力是最大的，离支座越远压应力越小;腹杆既有受拉的力也有受压的力，而最大拉应力也发生在靠近支座的两侧;同时发现所有杆件的应力都关于跨度方向的对称轴对称。

5 抽空正放四角锥双层柱面网壳结构的截面优化

对柱面网壳进行截面优化的目的是使网壳结构本身的自重最轻，这样既可以减少钢材的用量也可以使结构的整体造价更加经济。在对结构进行优化时，是不能改变网壳的网格布局、杆件的连接方式以及网壳整体外形的，同时还要满足结构的强度、刚度和稳定性。在此基础上进行杆件截面的优化，可以使杆件本身的承载能力得到最大限度的发挥。

对杆件截面进行优化其实就是通过不断改变杆件的截面面积，然后利用ANSYS软件计算杆件的应力值，在保证结构稳定的前提下，用最小的截面承担最大的应力。

在实际结构中，由于杆件的各种缺陷会使压杆的临界应力降低，所以对于最大压应力不仅要考虑强度、刚度，还需要验证其稳定性。

临界应力如式（1）[3]。

[σ]st=φ[σ]       （1）

式中：φ为稳定因数，可通过压杆柔度λ查表得到;[σ]为许用应;[σ]st为稳定许用应力。

压杆的柔度计算如式（2）[4]。

λ=μl/i        （2）

式中：μ为长度因数，这里取1;l为杆件的长度;i为压杆横截面对中性轴的惯性半径。

6 结语

在相同的条件下，正放抽空四角锥体系比正放四角锥体系压应力大而拉应力小，说明正放抽空四角锥结构的稳定性更好而且更加节约材料。正放抽空四角锥的最大拉压应力发生在靠近支座处，压应力最大值在上弦杆，拉应力最大值在腹杆;双层柱面网壳的最大位移发生在柱面网壳的中心处。柱面网壳杆件的应力关于长度方向的对称轴对称，同时也关于跨度方向的对称轴对称[5]。

参考文献：

[1] 中华人民共和国建设部.网壳结构技术规程：JGJ 612003[S].北京：中国建筑工业出版社，2003.

[2] 中华人民共和国住房和城乡建设部.建筑结构荷载规范：GB 50009—2012[S].北京：中国建筑工业出版社，2012.

[3] 孙训方，方孝淑，关来泰.材料力学[M].5版.北京：高等教育出版社，2009.

[4]张志国，张庆芳.钢结构[M].北京：中国铁道出版社，2013.

[5] 王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007.