一种直流侧带混合谐波抑制电路的24脉波整流器

陈涛，陈小强,2，米季炯，王英,2

一种直流侧带混合谐波抑制电路的24脉波整流器

陈涛1，陈小强1,2，米季炯3，王英1,2

(1.兰州交通大学自动化与电气工程学院，甘肃 兰州 730070; 2.光电技术与智能控制教育部重点实验室 (兰州交通大学), 甘肃 兰州 730070; 3.华北电力大学电气与电子工程学院, 北京 102206)

常规12脉波整流器会对电网造成大量谐波污染。为同时提高整流器交、直流侧电能质量，提出了一种直流侧带混合谐波抑制电路(Hybrid Harmonic Suppression Circuit, HHSC)的24脉波整流器。所提整流器由常规12脉波整流器、抽头变换器(Tapped Inter-Phase Converter, TIPC)和补偿电路(Compensation Circuit, CC)组成。TIPC的输出端与负载串联，直接调制整流桥的输出电流和电压。CC与负载并联，间接调制整流桥的输出电流，然后根据交、直流两侧电流关系和直流侧电压关系，最终使整流器输入电流接近正弦波，输出电压由12脉波倍增至24脉波。该方法仅需小容量(仅为输出功率的2.65%)的HHSC即可有效降低输入电流谐波和输出电压纹波，具有高谐波抑制性能、低谐波抑制代价等优点。在Matlab/Simulink中搭建仿真模型，验证了所提方法的正确性和有效性。

多脉波整流器；谐波抑制；电流直接注入；平衡电抗器；电能质量

0 引言

多脉波整流器(Multi-Pulse Rectifier, MPR)因结构简单、可靠性高、过载能力强等诸多优点，通常作为前端整流器广泛运用于可调速驱动器、船舶电力推进系统和多电飞机供电系统[1-4]。在众多MPRs中，12脉波整流器结构最简，运用最广[5-8]，然而12脉波整流器输入电流中包含大量的谐波，会对电网造成谐波污染，导致不满足IEEE-519标准要求[9-10]。另外，整流器的输出电压脉动较大，降低了直流供电质量[11-12]。

为降低12脉波整流器中的电流谐波，国内外学者提出了多种谐波抑制方法[13-22]，一般可分为两类。一类是被动谐波补偿方式，该方式通过安装有源、无源或混合电力滤波器来有效补偿整流器产生的谐波。然而，在一些场合中，滤波装置的容量与整流系统功率等级相当，故会导致损耗和成本增加[14-16]。另一类是主动谐波抑制方式，该方法通过改进整流器自身结构和控制方法力求从源头消除谐波。该方式可分为两种，一种是直流侧有源谐波抑制技术，它结合PWM控制技术，通过控制辅助开关变换器将直流侧电流调制为特定波形，然后根据交、直流两侧电流的对应关系，最终实现输入电流谐波的有效抑制。该方法虽然谐波治理效果显著，但不能增加输出电压的脉波数，对输出电压脉动无改善作用[17-19]。另一种是脉波倍增方法，其实现方式有两种，一种是通过细分移相变压器的移相角来增加输出电压相数，进而增加整流器的脉波数。根据此方法，文献[20-22]分别提出了18、20、和24脉波整流器，与常规12脉波整流器相比，它们均有效地降低了输入电流的谐波总畸变率和输出电压的纹波系数。然而，多相变压器结构复杂，绕组与整流元件个数倍增，这不仅增加了整流器的成本、体积和制造难度，而且导致谐波抑制效率急剧下降。为在尽量不增加整流器复杂性的前提下实现脉波倍增，抽头平衡电抗器(Tapped Inter-Phase Reactor, T-IPR)被提出用于将常规12脉波整流器扩展到24脉波整流器[23-26]。该方法利用抽头上二极管的交替导通，在直流侧调制生成不流经负载的环流，进而增加整流桥的输出电流状态，然后依据交、直流两侧电流关系和直流侧电压关系，最终将整流器的输入电流阶梯数和输出电压脉波数从12提高到24，实现对输入电流谐波和输出电压纹波的抑制。然而，该方法谐波抑制能力有限，虽然它能抵消输入电流中的11、13次谐波，但高次谐波的含量仍然很高，不满足相关谐波标准要求。另外，由于直流侧环流特征的局限性，整流桥输出电流没有到达零的时刻，整流器可能存在因换相重叠而导致的电压陷波问题[27]。

为此，本文提出一种直流侧带混合谐波抑制电路(Hybrid Harmonic Suppression Circuit, HHSC)的24脉波整流器，它由常规12脉波整流器、基于有源抽头电抗器(Active-Tapped Inter-Phase Reactor, AT-IPR)的变换器(Tapped Inter-Phase Converter, TIPC)和补偿电路(Compensation Circuit, CC)组成(如图1 所示)。与基于T-IPR的方案相比，CC的引入不仅可以有效抑制整流器中高次谐波，提高谐波抑制能力，而且CC与TIPC的共同调制使得整流桥可以零电流换相，有利于避免换相重叠问题。

1 整流器拓扑及其工作模态

1.1 整流器电路结构

图1所示为所提出的直流侧带HHSC的24脉波整流器拓扑。除了HHSC取代常规平衡电抗器外，整流器几乎与常规12脉波整流器相同。整流器采用星形自耦变压器作为移相变压器(Auto-Transformer for Phase-Shifting, ATPS)，利用零序电流阻抗器(Zero Sequence Blocking Transformer, ZSBT)抑制三倍频电流。AT-IPR抽头与两个共阴极二极管相连组成TIPC，TIPC与负载串联，产生无源环流t；CC与负载并联，产生补偿环流s。由t与s配比形成的复合环流m首先调制整流桥(REC I, REC II)的输出电流(d1,d2)，然后根据交、直流两侧电流关系和直流侧电压关系，最终降低整流器的输入电流谐波和输出电压纹波。

图1 直流侧带HHSC的24脉波整流器

为便于后续理论分析和计算，先做以下假设。

1) 整流器三相输入电压为

式中，m为输入相电压有效值。

2) 图2为AT-IPR的绕组结构。定义AT-IPR的抽头匝比n为

3) 忽略ATPS和AT-IPR的漏感。

4) 整流器工作在大电感负载状态，即负载电流d可以看作一个恒定的d。

1.2 HHSC的工作模态

由图1可以得到HHSC具有四种工作模态，如图3所示。

图3 HHSC工作模态

由图3得到对应工作模态下直流侧电压关系及环流形式，如表1 所示。

表1 HHSC工作模态下直流侧电压关系和环流

2 混合谐波抑制机理分析

2.1 输入电流特性

根据TIPC的工作原理，并结合表1，直流侧复合环流m可以表示为

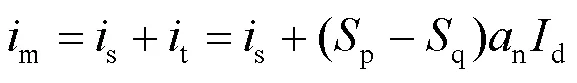
式中，p和q分别为TIPC中Dp和Dq的开关函数，其表达式为

式中，为自然数。

根据整流系统对称性，REC I和REC II的输出电流由m决定，即

依据整流桥调制原理，REC I和REC II的输入、输出电流之间满足

式中，a1、b1、c1、a2、b2和c2分别是a1、b1、c1、a2、b2和c2相的开关函数。其中，a1的波形如图4所示。

a1与各开关函数之间的关系满足式(7)。

根据图1中星形自耦变压器绕组结构关系，可以得到整流器的输入电流a为

输入电流a的谐波总畸变率ia可以表示为

式中，a和af分别为a及其基波电流af的有效值，它们可借助式(10)计算。

综合上述分析，直流侧复合环流m是影响整流器输入电流特性(电流各次谐波含量和谐波总畸变率)的决定因素。

2.2 输出电压特性

同样地，依据调制原理，REC I和REC II的输出电压满足

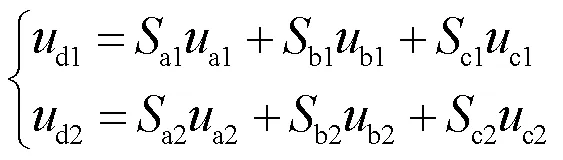
式中，a1、b1、c1、a2、b2和c2为整流桥对应相的输入电压，结合式(1)和星形变压器的电压相量关系，它们可以表示为

结合表1中电压关系和式(4)，整流器的输出电压d可表示为

结合式(7)和式(11)—式(13)，得到d表达式为

输出电压d的纹波系数u可以表示为

根据上述分析，整流器的输出电压特性(输出电压及其纹波系数)与n有关。

2.3 CC容量特性

图1中的AT-IPR的端电压可以计算为

因此，CC的容量可表示为

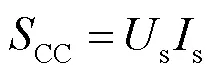
式中，s、s分别为s和s的有效值，可分别通过式(18)和式(10)计算。

定义CC的等效容量为

式中：d为整流系统输出功率；d为负载电压d的有效值。

根据上述分析，CC的容量取决于补偿环流s。

3 混合谐波抑制策略效能及参数优化

3.1 环流部分补偿原理

根据前面分析，直流侧环流特征是抑制输入电流谐波的决定因素。在文献[19]中大电感负载下，当环流p(见图5)满足特定条件(幅值为0.5d，与a同相位，频率为300 Hz的三角波，且其负向过零点恰好是a的正向过零点)时，能最大程度降低输入电流谐波。因此，本文借鉴文献[19]中的谐波抑制思想，提出基于环流部分补偿(Circulating Current Partial-Compensation, CCPC) 策略的混合谐波抑制方法，力争使直流侧复合环流成为上述三角波环流p，环流补偿原理如图5所示。

图5 环流补偿原理示意图

图5中，CC产生s对t的幅值不足部分进行补偿，即CC仅对阴影三角形部分补偿。1为t的幅值，2为t的宽度(电源周期的1/12)。

图5中，p的傅里叶级数展开式为

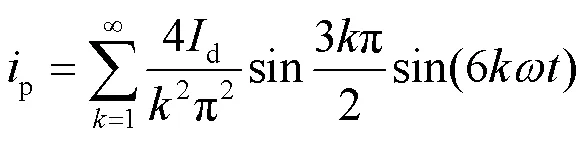
由式(3)可知，t的幅值2­取决于n，即

由CCPC原理可知，1和2关系满足

利用图5中的几何关系，1满足

基于上述约束条件，所需补偿电流s为

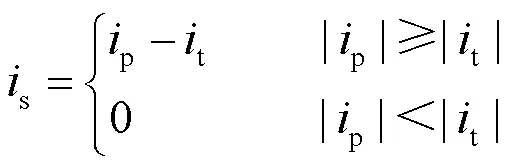
3.2 环流配比分析及关键参数优化

根据上述分析可知，混合谐波抑制效能取决于由n所决定的t波形以及由CC产生的s波形。因此，本文所提混合谐波抑制的关键是设计适当的匝比n和补偿环流s。同时，补偿环流s是在无源环流t的基础上进行叠加的，所以，补偿环流s的波形也取决于n，即n是环流配比的决定因素。

为探究不同环流配比下整流器的工作特性，以n为自变量，根据环流补偿原理对不同的n值决定的t采取与之对应的s波形进行补偿，建立了n与ia、u和c之间的关系，如图6所示。

图6中，随着n的增大，即AT-IPR抽头向两端移动时，无源环流t的幅值增加，对应补偿环流s的幅值减小，导致CC的等效容量c降低，输入电流的谐波总畸变率不断增大，输出电压的纹波系数先减小后增大。

图6 an与THDia、RFu和λc的关系曲线

依据IEEE-519标准对电能质量的要求，并结合文献[3]中整流器的设计准则，给出了整流器具有良好性能的工作范围，如图6中阴影部分所示。阴影部分满足：整流器的ia小于6%，u小于0.5%，c低于1%。

值得注意的是，当u取得最小值时，ia和c均处于阴影部分范围内。因此，本文将此时对应的n值作为AT-IPR的最优抽头匝比，进而可以得到最优补偿电流s的波形。

对式(14)和式(15)推导运算，得到u最小值时的n值为

因此，结合式(14)、式(18)和式(25)，可以得到整流器的输出电压和输入电压的有效值满足式(26)。

4 整流系统工作特性分析

4.1 主要电流特性

图5中，定义补偿的阴影三角形部分宽度占比为

结合环流补偿原理和式(27)，可以得到ia随变化的规律，如图7所示。

图8给出了最优环流配比下整流器中主要电流波形。从图8中看出，优化设计的补偿电流s波形是六倍电网频率的周期波，在s的作用下，直流侧复合环流m被调制为准三角波电流，进而影响整流桥输出电流d1和d2的波形，最终使得整流器的输入电流a接近正弦波，其谐波总畸变率为5.37%。此外，从d1和d2波形可以看出，整流桥中二极管在换相时电流降为零，因此，所提方法能使整流桥零电流换相。

根据式(9)对最优环流配比时输入电流a进行傅里叶级数展开，得到其各次谐波含量。表2为常规12脉波整流器[5]和所提整流器中输入电流谐波含量的对比结果。

图8 整流器的主要电流波形

从表2中可以看出，使用所提方法后，整流器的输入电流中主要包含12±1特征次谐波，各次谐波的含量均显著降低。

表2 输入电流谐波含量对比

4.2 主要电压特性

图1中ZSBT的端电压可表示为

式中，m2n和m4n分别为m2和m4点电位，它们可以表示为

根据式(11)—式(16)、式(25)—式(26)和式(30)—式(32)，得到整流器中主要电压波形，如图9所示。

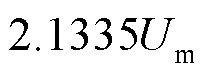
4.3 HHSC容量特性

1) 基于AT-IPR的TIPC容量

根据图8和式(10)，可以得到

结合图8—图9、式(10)和式(18)，可以得到s、s和m的有效值分别为

因此，基于AT-IPR的TIPC容量可计算为

2) CC的容量

因此，HHSC容量仅占负载输出功率的2.65%。

5 CC的设计原理及控制方法

由上述分析可知，为保证整流器的谐波抑制效能和能量转化效率，HHSC中的CC应该具备两个功能：1) 能快速跟踪整流器负载电流的变化，及时调整补偿电流s的幅值，使其满足图8中的参考电流信号要求；2) 能将补偿的功率(cc)回馈给负载，降低能量损失。考虑以上要实现的功能，选用具有升压功能并可四象限运行的单相全桥PWM 变换器作为CC的主电路。由于CC的输出端与负载并联，而负载两端电压由整流系统主电路决定，因此CC仅需一个电流控制环，只要对电路和控制器参数(见表3)进行合理设计后，能使电流控制精度高，动态响应快。

表3 系统主要参数

图10为单相全桥 PWM 变换器控制电路的Simulink模型。PLL锁相环检测电压信号ab的相位和频率，输出300 Hz的同步信号，经Lookup Table模块查表确定参考信号的波形，再乘以负载电流的幅值，得到参考电流信号；将参考电流信号与采样电流信号做差，通过三角波比较器产生PWM信号驱动开关管。

6 仿真分析与对比验证

为验证上述分析的正确性及所提混合谐波抑制方法的有效性，基于Matlab/Simulink搭建了如图1所示的整流系统仿真模型，其系统主要参数见表3。

6.1 混合谐波抑制效果

图10 单相全桥 PWM 变换器控制电路的Simulink模型

图11 整流器的输入电流及其频谱分析和输出电压

图12为所提整流器中主要电流波形。图12中仿真实验波形与图8中理论分析波形一致。补偿电流s为6倍电网频率的周期波；由于HHSC的调制，整流桥输出电流出现零时刻，整流桥可以实现零电流换相。

图13为所提整流器中主要电压波形。图13中仿真实验波形与图9中理论分析波形一致。AT-IPR的端电压波形为300 Hz的三角波；由于ZSBT抑制了电路中的3倍频电流，导致ZSBT的端电压波形为3倍电网频率的三角波。

图13 整流器中主要电压

6.2 额外损耗评估

所提整流器中采用HHSC取代了常规平衡电抗器，因此，额外损耗主要包括TIPC损耗和CC损耗。

1) TIPC中二极管导通损耗

根据文献[6]中二极管损耗的计算准则，并结合TIPC工作模态，其额外导通损耗可表示为

式中，d、av分别为二极管导通压降和平均电流。

2) CC中开关管功率损耗

单相全桥PWM变换器运行在高开关频率下，主要的功率损耗为开关损耗和关断损耗，其损耗之和可表示为

式中：DS为漏源直流电压；D为漏极直流电流；on、off分别为开通延迟时间和关断延迟时间。

根据器件数据手册，选用800 V/7.8的IRFPE50作为开关管进行分析，则式(37)中参数满足式(38)。

因此，一个电源周期内的开关管损耗为s= 2.1 W，其占输出功率比为：2.1/(294×10)=0.07%。

6.3 与基于T-IPR的谐波抑制方法比较

图14为T-IPR的电路原理图和绕组结构图。

图14 T-IPR电路原理图与绕组结构图

基于本文和T-IPR方案相关文献的分析，图15给出了常规12脉波整流器分别使用基于T-IPR的谐波抑制方法和所提方法后整流器输入电流中谐波含量对比结果。

图15 谐波含量对比结果

在表3所示的相同条件下，得到基于T-IPR的整流器工作特性，如图16所示。

图16中，基于T-IPR的整流器运行在24脉波整流状态，输入电流为24阶梯波，其包含大量的24±1次谐波，ia值为7.13%，因变压器漏感的影响，其略低于理论值(7.56%)。同样，整流器输出电压为24脉波，电压脉动小。然而，基于T-IPR的谐波抑制方法导致整流桥输出电流近似为矩形波，没有到达零的时刻，这表明基于T-IPR的整流器易出现换相重叠问题。

图16 基于T-IPR的整流器工作特性

通过上述分析，表4给出了基于T-IPR的整流器和所提整流器的谐波抑制性能对比结果。

表4 与基于T-IPR的整流器谐波抑制性能对比

Table 4 Comparison of the harmonic suppression performance between the proposed rectifier and T-IPR

由表4可知，所提方案中AT-IPR与CC并联，复杂度增加，二者平衡电抗器抽头数相同，但AT-IPR容量更低，仅占负载输出功率的1.83%。由于小容量(0.82%d)CC的功率损耗仅为0.07%d，其总额外损耗与T-IPR的方案相近。所提方案有利于避免换相重叠问题，且能有效抑制输入电流中的高次谐波。此外，与T-IPR方案相比，所提方案具有相同的输出电压脉波倍增能力，更强的输入电流谐波抑制能力，ia更低。

值得注意的是，由于本文所研究整流器中主要整流器件是二极管，负载电压不能改变。为实现可变电压功能，需要级联一个斩波电路(DC-DC变换器)，可能会增加整流器的损耗。当然，使用晶闸管替代二极管可改变多脉波整流器的负载电压。但负载电压的变化会降低整流器的位移因数，而当使用额外设备提高位移因数时，也会增加功率损耗。因此，本文研究成果通常作为前端变换器运用于船舶推进、全电飞机/多电飞机和电机驱动等大功率变换系统的整流部分。

7 结语

为进一步抑制12脉波整流器的输入电流谐波和输出电压纹波，本文提出了一种直流侧基于CCPC策略的混合谐波抑制方法，得到了一种高谐波抑制性能的新型24脉波整流器。分析了其工作模态，明确了 HHSC对整流器输入电流和输出电压的调制作用，推导了AT-IPR的最优匝比，得到了最佳环流配比，计算了磁性元件的电压、电流等级和容量，评估了整流器额外损耗。最佳环流配比条件下，HHSC将整流器输入电流的谐波总畸变率降低至原来的1/3左右，输出电压的纹波系数减少至原来的1/4，有效降低了输入电流谐波和输出电压纹波。

[1] DU Q, GAO L, LI Q, et al.Harmonic reduction methods at DC side of parallel-connected multipulse rectifiers: a review[J].IEEE Transactions on Power Electronics, 2021, 36(3): 2768-2782.

[2] 孟凡刚, 杨世彦, 杨威.多脉波整流技术综述[J].电力自动化设备, 2012, 32(2): 9-22.

MENG Fangang, YANG Shiyan, YANG Wei.Overview of multi-pulse rectifier technique[J].Electric Power Automation Equipment, 2012, 32(2): 9-22.

[3] CHEN Y, SHEN J, CHEN H, et al.Evaluation on the autoconfigured multipulse AC/DC rectifiers and their application in more electric aircrafts[J].IEEE Transactions on Transportation Electrification, 2020, 6(4): 1721-1739.

[4] 李亚辉, 孙媛媛, 李可军, 等.不平衡供电条件下多脉动整流器的谐波特性分析[J].电力系统自动化, 2021, 45(23): 152-161.

LI Yahui, SUN Yuanyuan, LI Kejun, et al.Harmonic characteristic analysis of multi-pulse rectifier under unbalanced power supply condition[J].Automation of Electric Power Systems, 2021, 45(23): 152-161.

[5] 孟凡刚, 朱春波, 高蕾, 等.基于星形联结自耦变压器的高功率密度12脉波整流器研究[J].电机与控制学报,2018, 22(8): 1-9.

MENG Fangang, ZHU Chunbo, GAO Lei, et al.High-power density 12-pulse rectifier based on star-connected autotransformer[J].Electric Machines and Control, 2018, 22(8): 1-9.

[6] KALPANA R, SINGH B.Inclusive design and development of front-end multiphase rectifier with reduced magnetic rating and improved efficiency[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2989-3000.

[7] 王涛, 彭国荣, 胡隽璇, 等.基于谐波磁势平衡的12脉波整流器一体化滤波方法[J].电力系统自动化, 2020, 44(8): 157-167.

WANG Tao, PENG Guorong, HU Junxuan, et al.Integrated filtering method of 12-pulse rectifier based on harmonic magnetic potential balance[J].Automation of Electric Power Systems, 2020, 44(8): 157-167.

[8] 郑春菊, 孟鑫, 周群, 等.三相多驱动系统带移相电流控制的谐波消除方法[J].电力系统保护与控制, 2021, 49(12): 114-123.

ZHENG Chunju, MENG Xin, ZHOU Qun, et al.Harmonic elimination method with phase-shifted current control in a three-phase multi-drive system[J].Power System Protection and Control, 2021, 49(12): 114-123.

[9] 李振华, 胡廷和, 杜亚伟, 等.一种优化窗函数及其在电网谐波检测中的应用分析[J].高压电器, 2020, 56(10): 239-246, 252.

LI Zhenhua, HU Tinghe, DU Yawei, et al.Optimal window function and its application in harmonic detection of power grid[J].High Voltage Apparatus, 2020, 56(10): 239-246, 252.

[10] MOHAMED A.High performance decoupled active and reactive power control for three-phase grid-tied inverters using model predictive control[J].Protection and Control of Modern Power Systems, 2021, 6(3): 311-329.

[11] 耿晓红, 文俊, 谈萌, 等.高电缆化率对直流受端输电网谐波传递特性的影响[J].电力建设, 2020, 41(1): 106-113.

GENG Xiaohong, WEN Jun, TAN Meng, et al.Impact of high cable rate on harmonic transfer characteristics of transmission power grid at HVDC receiving-end[J].Electric Power Construction, 2020, 41(1): 106-113.

[12] 袁义生, 陈旭, 毛凯翔.基于纹波电压前馈的级联H桥整流器输出电压平衡策略[J].电力系统保护与控制, 2020, 48(2): 9-17.

YUAN Yisheng, CHEN Xu, MAO Kaixiang.Output voltage balance strategy based on ripple voltage feedforward for cascaded H-bridge rectifier[J].Power System Protection and Control, 2020, 48(2): 9-17.

[13] 白雪, 高瑞雪, 闻福岳, 等.特定次谐波注入抑制模块化多电平换流器电容电压波动[J].电网与清洁能源, 2020, 36(9): 8-14.

BAI Xue, GAO Ruixue, WEN Fuyue, et al.Suppression of capacitor voltage fluctuation of the modular multilevel converter by specific sub-harmonic injection[J].Power System and Clean Energy, 2020, 36(9): 8-14.

[14] 王雪, 高云广, 吝伶艳, 等.有源电力滤波器的研究现状与展望[J].电力系统保护与控制, 2019, 47(1): 183-192.

WANG Xue, GAO Yunguang, LIN Lingyan, et al.Research status and prospect of active power filter[J].Power System Protection and Control, 2019, 47(1): 183-192.

[15] 杨剑锋, 王晓庆.混合型多APF系统建模及共振抑制方案研究[J].电力系统保护与控制, 2021, 49(15): 68-75.

YANG Jianfeng, WANG Xiaoqing.Study on modeling of a hybrid multi-APFs system and resonance suppression scheme[J].Power System Protection and Control, 2021, 49(15): 68-75.

[16] 孙巍峰, 崔晨, 周晓风, 等.调相机与特高压直流换流站交流滤波器的协调控制策略[J].电力系统保护与控制, 2020, 48(7): 182-187.

SUN Weifeng, CUI Chen, ZHOU Xiaofeng, et al.Coordinated control strategy for synchronous condenser and AC filter in UHVDC converter station[J].Power System Protection and Control, 2020, 48(7): 182-187.

[17] SHEELVANT V, KALPANA R, SINGH B.Improvement in harmonic reduction of a zigzag autoconnected transformer based 12-pulse diode bridge rectifier by current injection at dc side[J].IEEE Transactions on Industrial Application, 2017, 53(6): 5634-5644.

[18] 孟凡刚, 骆霁嵘, 高蕾, 等.基于直流侧有源谐波抑制方法的高功率密度多脉波整流器[J].电工技术学报, 2017, 32(19): 134-140.

MENG F, LUO Jiarong, GAO Lei, et al.A high power density multi-pulse rectifier based on harmonic reduction technology at DC link[J].Transactions of China Electrotechnical Society, 2017, 32(19): 134-140.

[19] MENG F, YANG W, YANG S, et al.Active harmonic reduction for 12-pulse diode bridge rectifier at DC side with two-stage auxiliary circuit[J].IEEE Transactions on Industrial Informatics, 2015, 11(1): 64-73.

[20] 陈涛, 陈小强, 王英, 等.一种新型升压18脉波自耦变压整流器的研究[J].电网技术, 2021, 45(4): 1527-1535.

CHEN Tao, CHEN Xiaoqiang, WANG Ying, et al.Research on a novel step-up 18-pulse auto-transformer rectifier unit[J].Power System Technology, 2021, 45(4): 1527-1535.

[21] SARAVANA P P, KALPANA R, SINGH B, et al.A 20-pulse asymmetric multiphase staggering autoconfigured transformer for power quality improvement[J].IEEE Transactions on Power Electronics, 2018, 33(2): 917-925.

[22] KHAN S, ZHANG X, ALI H, et al.A novel 24-pulse rectification system[J].IEEE Access, 2018, 6: 59350-59361.

[23] PAN Q, MA W, LIU D, et al.A new critical formula and mathematical model of double-tap interphase reactor in a six-phase tap-changer diode rectifier[J].IEEE Transactions on Industrial Electronics, 2007, 54(1): 479-485.

[24] LIAN Y, YANG S, XU K, et al.Harmonic reduction mechanism at DC link of two different 24-pulse rectifiers[C] // 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), August 7-10, 2017, Harbin, China: 1-6.

[25] SINGH B, KASAL G K, GAIROLA S.Power quality improvement in conventional electronic load controller for an isolated power generation[J].IEEE Transactions on Energy Conversion, 2008, 23(3): 764-773.

[26] CHEN C, HORNG G.A new passive 28-step current shaper for three-phase rectification[J].IEEE Transactions on Industrial Electronics, 2000, 47(6): 1212-1219.

[27] 刘一论, 刘进飞, 高红均.一种抑制多馈入直流系统后续换相失败的低压限流单元参数优化策略[J].电力建设, 2021, 42(5): 122-129.

LIU Yilun, LIU Jinfei, GAO Hongjun.A method for optimizing the VDCOL parameter to suppress the subsequent commutation failure of multi-infeed HVDC system[J].Electric Power Construction, 2021, 42(5): 122-129.

A 24-pulse rectifier with hybrid harmonic suppression circuit on the DC side

CHEN Tao1, CHEN Xiaoqiang1,2, MI Jijiong3, WANG Ying1,2

(1.School of Automation & Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2.Key Laboratory of Opto-Technology and Intelligent Control Ministry of Education (Lanzhou Jiaotong University), Lanzhou 730070, China;3.School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

The conventional 12-pulse rectifier causes a lot of harmonic pollution in the grid.To improve the power quality of both AC and DC sides of the rectifier, a 24-pulse rectifier with hybrid harmonic suppression circuit (HHSC) on the DC side is proposed.The proposed rectifier consists of a conventional 12-pulse rectifier, an active-tapped inter-phase reactor (AT-IPR) and a compensation circuit (CC).The output side of the TIPC is connected in series with the load to directly modulate the output current and output voltage of the rectifier bridge; the CC is connected in parallel with the load to indirectly modulate the output current of the rectifier bridge, and then according to the current relationship between the AC and DC sides and the voltage relationship on the DC side, the input line current of rectifier is close to the sinusoidal current andoutput voltage is doubled from 12 to 24 pulses.This method only needs a small-capacity HHSC (only 2.65% of output power) to reduce input line current harmonics and output voltage ripple effectively, and it has the advantages of high harmonic suppression performance and low harmonic suppression cost.The simulation model of the rectifier system is built in Matlab/Simulink to verify the correctness and effectiveness of the proposed method.

multi-pulse rectifier; harmonic suppression; direct current injection; inter-phase reactor; power quality

10.19783/j.cnki.pspc.210859

2021-08-11；

2021-09-30

陈 涛(1995—)，男，硕士研究生，研究方向为电能质量变换与控制及其谐波抑制；E-mail: ct0219338@163.com

陈小强(1966—)，男，通信作者，研究方向为大功率整流器的谐波抑制。E-mail: xqchen@mail.lzjtu.com

国家自然科学基金项目(51767013，52067013)；教育部光电技术与智能控制重点实验室开放课题(KFKT2020-12)

This work is supported by the National Natural Science Foundation of China (No.51767013 and No.52067013).

(编辑 姜新丽)