基于Bagging集成学习的电力系统暂态稳定在线评估

赵冬梅，谢家康，王 闯，王浩翔，姜 威，王 怡

基于Bagging集成学习的电力系统暂态稳定在线评估

赵冬梅1，谢家康1，王 闯1，王浩翔1，姜 威2，王 怡1

(1.华北电力大学电气与电子工程学院，北京 102206；2.中国华能北方魏家峁煤电有限责任公司，内蒙古 鄂尔多斯 010308)

针对传统机器学习在处理暂态稳定评估时所表现出的稳定性差、精度低等问题以及离线训练的局限性，提出一种基于多模型融合Bagging集成学习方式的电力系统暂态稳定在线评估模型。首先，结合人工智能前沿理论研究，分析了暂态稳定评估中常用的7种机器学习算法的原理及实现方式，通过Bagging方法进行集成，充分发挥各个模型的优势。其次，给出Bagging集成的数学实现方法并进行了仿真实验。当原系统拓扑结构发生改变时，采用Boosting算法和迁移成分分析，分别对原电网历史数据进行样本迁移和特征迁移，完成对所提模型的在线更新。通过采用IEEE10机39节点系统和IEEE16机68节点系统进行分析，结果表明所提方法比传统机器学习模型精度更高。当数据中掺杂噪声时能够保持稳定运行，在系统拓扑改变时能够通过迁移历史数据进行准确的暂态稳定评估。

Bagging集成学习；电力系统；机器学习；暂态稳定；迁移学习；在线更新

0 引言

电力系统暂态稳定评估(Transient Stability Assessment, TSA)是保障电力系统安全性和提升电力系统经济性的重要手段[1-3]。随着电网规模逐渐增大以及电网结构日渐复杂，电力系统运行工况更加接近稳定极限，如何进行电力系统的TSA，将成为电网设计人员在设计电网结构时所要考虑的重要内容。

由于电网中广域测量系统(Wide Area Measurement System, WAMS)和电源管理单元 (Power Management Unit, PMU)的不断普及，电力系统已经拥有了获取大量实时运行时的电力数据的能力[4-5]。随着新能源不断并网，系统规模越来越复杂，当前电力系统的新发展对TSA提出了更高要求，传统方法(如时域仿真法)在适用范围、评估及预测的速度等方面面临严峻挑战。机器学习的发展为二者的突破提供了新的可能，基于机器学习的TSA方法成为电力系统研究领域的前沿课题[6]。

与传统的TSA方法相比，机器学习方法从模式识别的角度出发，通过自主训练模型建立电力系统物理量与评估结果之间的映射关系，然后用训练好的模型对系统中新产生的样本进行分析[7]。近年来，国内外已经有众多学者对基于机器学习的电力系统TSA进行了分析与改进。如文献[8]基于支持向量机(Support Vector Machine, SVM)的TSA模型、文献[9]的基于随机森林(Random Forests, RF)、K值近邻(K Nearest Neighbor, KNN)的TSA模型、文献[10-11]建立的人工神经网络(Artificial Neural Network, ANN)的TSA模型、梯度提升决策树(Gradient Boosting Decision Tree, GBDT)、逻辑回归(Logistic Regression, LR)、自适应提升算法(Adaptive boosting machine, Adaboost)等。

但这些训练模型大部分是浅层学习，对数据挖掘的能力有限，处理大型数据时的精度不高，除浅层学习之外，机器学习还有一个分支领域——深度学习[12]，它强调从连续的层中进行学习，逐次改善模型的深度，以达到更好的预期效果。常见算法如卷积神经网络(Convolution Neural Network, CNN)[13]、堆叠变分自动编码器(Sparse Stacked Auto Encoder, SSAE)、长短期记忆网络(Long Short Term Memory network, LSTM)等。如文献[14]提出的基于卷积神经网络的TSA模型，文献[15]利用堆叠变分自动编码器进行电力系统暂态稳定评估，由于单一模型的预测结果存在偏好，不同学习器的预测结果存在差异，所以单一模型训练出的分类器存在一定的局限性。并且电网实时信息在传输时会产生噪声，而单一模型的抗噪能力较弱，无法与深度学习算法相比较。故使用多模型的集成算法在近年来被广泛研究，如文献[16]建立的基于集成LSTM的TSA模型。文献[17]基于在线Boosting集成连续极限学习机(Ensemble Online Sequential-extreme Learning Machine, EOS-ELM)的TSA模型。虽然以Boosting算法为代表的集成学习模型在TSA中取得了良好的应用效果，但其单一算法Boosting集成的局限性依然存在，且单个深度学习模型的训练时间较长，多次训练Boosting集成将会降低TSA速度，使得模型效率降低。本文提出了一种对多种机器学习算法进行二次学习的Bagging集成学习算法，经过验证，基于多学习器融合方法的Bagging集成不仅能够适应大型系统的暂态稳定训练，具有良好的抗噪性，而且与传统深度学习方法相比，其精度、准确度更高，模型性能更好。

由于电力系统是一个动态时变的系统，仅作为离线训练评估暂态稳定结果还远远不够，国内外有不少学者对已有模型的在线更新方法进行了研究，如文献[17]利用Boosting算法原理对TSA模型进行特征迁移，但在特征维度较大时，这种利用弱分类器自主训练的贪婪算法会导致模型迁移时间过长。本文针对迁移学习的两大主流思想，提出基于特征迁移的迁移成分分析(Transfer Component Analysis, TCA)算法和基于样本迁移的Boosting迁移算法，通过两种不同的角度对所提模型进行迁移，并通过IEEE10机39节点及IEEE16机68节点系统的仿真算例验证了所提方法的有效性。

1 算法原理

1.1 机器学习

1.1.1支持向量机

支持向量机是通过使数据符合某种未知但固定的分布时，使得分类器的真实输出与理想输出的误差尽可能小的算法。通过最大间隔法从特征空间内找到最优高维平面来解决分类或优化问题。适用于高维大型数据集。

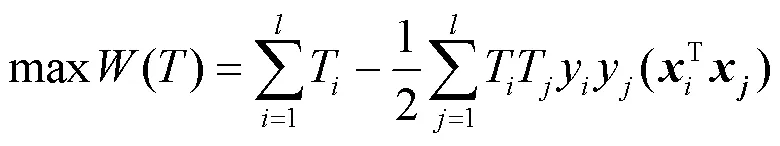
要求同时满足：

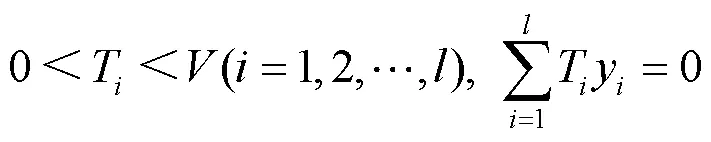
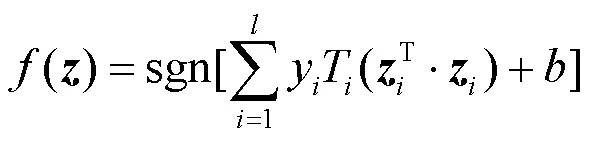
1.1.2人工神经网络

人工神经网络[18]是一种利用误差函数反向传播方式进行学习的监督式机器学习算法。

目标函数使得输入标签和输出结果尽可能相似，可以采用欧式距离损失函数作为目标函数进行寻优，其表达式为

1.1.3随机森林与梯度提升决策树

随机森林算法[19]是由多个决策树集成而来的一种新兴学习算法，依靠决策树的投票来决定最后的分类结果，近年来在各个领域都得到了广泛的应用。

梯度提升决策树也是一种基于决策树的算法，由多个DT算法组成，树的结论累加得到最终答案。与随机森林算法类似，这里不再赘述。

1.1.4 K值近邻法

K值近邻采用多个维树(K-dimensional Tree, KD Tree)的方法求取输入样本的方差，找到划分的特征点后，将超平面分为多个部分，不同部分对应不同标签所对应的类别，从而达到训练分类的目的。

K值近邻法判别样本的权重公式为

1.1.5 Logistic回归

Logistic算法是引入概率论中极大似然估计的方法，求得类似神经网络中的权值和偏移量参数，进而达到训练分类的目的。

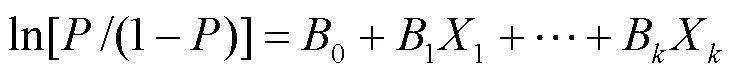
1.1.6 Adaboost算法

4) 计算预测错误率。

6) 更新权重系数。

7) 迭代完成后输出预测结果。

1.2 Bagging集成学习

在机器学习的有监督学习算法中，其目的是训练出一个稳定且在各个方面都表现较好的模型，但实际情况往往并不理想，有时只能得到一些有偏好的模型，这些模型在某些方面表现得比较好，属于弱监督模型。本文提出的集成学习模型通过组合这些已有的弱监督模型得到一个性能更好、更全面的强监督模型。这样，即使某一个弱分类器在测试自己所不擅长的数据集时发生错误，其他弱分类器也能够及时将错误纠正过来。

集成学习[20]是将几种机器学习技术组合成一个预测模型的元算法，以减小各个模型的方差、偏差，或改进预测的效果。其总体结构：先通过训练多个基学习器，再用某种策略将这些基学习器结合。集成学习通过集成多个基学习器，取长补短，可获得比单一学习器更加优越的性能。

由基学习器[21]的生成方式，集成学习可分为两类：一类是以Boosting为代表的，各基学习器间存在依赖关系，必须串行生成的集成学习算法；另一类是以Bagging为代表的，各学习器间不存在依赖关系，可以并行生成的集成学习算法，如图1所示。

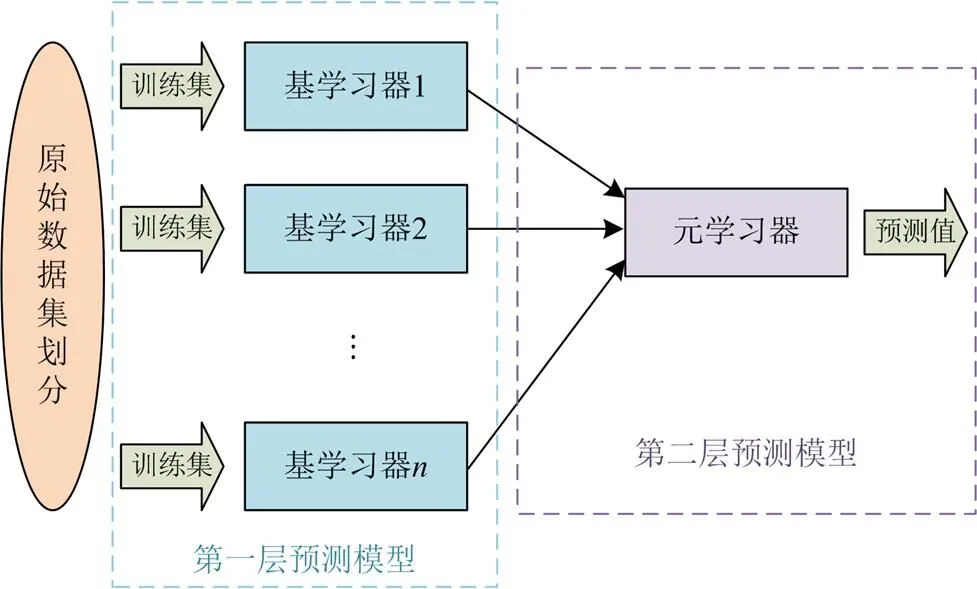
图1 Bagging集成学习结构

Bagging算法[22]是并行集成学习的经典算法。为了使集成的基学习器尽可能独立。Bagging算法可以通过自助采样法随机从输入的数据集中摘出多个训练子集，然后根据训练子集训练出多个基学习器，最后将基学习器结合，形成一个整体。

但是，自助采样法主要是针对数据集较小的情况，当数据量较大时，采用自助采样法反而会造成因数据量缺失而导致的学习器精度下降。所以，本文采用遍历方法，将原始数据分别导入7个训练器中进行训练，最终通过集成方法得到总分类器。

对于不同的集成学习而言，集成方法可以有很多。例如：可以将不同学习器得到的函数值求平均得到最终结果，也可以通过加权平均求得。本文通过不同模型的训练，得到不同模型样本数据集的预测值，根据这些预测值与训练数据的标签，代入新的机器学习模型中进行二次训练，最后用测试集对其进行检验。这就是本文对多分类器结果进行集成的思路。集成学习训练流程部分的伪代码如下。

输出：Bagging集成学习模型

步骤2：对第一层7个基学习器进行训练

end

步骤3：构建新数据集

步骤5：将测试集导入模型得出预测结果

2 模型在线更新

随着智能电网的发展，电力系统所需要记录的数据规模越来越大，系统特征越来越多。但是这些数据的利用率并不高，其主要原因在于电力系统是一个时变性系统，其时变性体现在数据时变、系统结构时变等多个方面。随着深度学习的不断发展，如何利用好历史数据是提高暂态稳定评估效率的一个重要问题。

迁移学习在人工智能和机器学习中是指一种学习的思想和模式。机器学习解决的问题是让机器能够自主的从数据中获取知识，通过输入数据和结果得到数据与结果之间的映射关系。而迁移学习作为机器学习的一个重要分支，侧重于将已经学习过的知识迁移应用到新的问题当中。其核心问题在于找到新问题和原问题之间的相似性，才可以顺利实现知识的迁移。那么，如何衡量源域和目标域中相应数据的相似性便成了解决该问题的重要一步。

迁移学习的基本方法包括样本迁移、特征迁移、模型迁移以及关系迁移。

本文就迁移学习中比较前沿的两种方法进行了实验。第一种是基于样本的迁移学习方法，根据一定的权重生成规则，对数据样本进行重复使用来进行迁移学习，如TrAdaboost方法[23]。第二种是基于特征的迁移方法，是指通过特征变换的方式互相迁移，来减少源域与目标域之间的差距，如文献[24]所提出的迁移成分分析。

Boosting迁移算法[25]假设源域与目标域的数据使用同样的特征与标签，但是两个领域上的数据分布不同。这样使得一些源领域数据对目标领域的影响也不同。如TrAdaBoost算法正是在AdaBoost算法的基础上，对源域的特征进行加权、迭代，每一次加权训练一个分类器，通过该分类器的性能好坏决定权重的更新策略，其算法流程如图2所示。

图2 TrAdaBoost算法结构图

迁移成分分析算法作为一种边缘分布自适应算法，其目标在于减小源域和目标域边缘概率分布的距离，从而达成迁移学习的目的，属于特征迁移方法。通过设定一个距离函数作为目标值，并建立以该函数为目标函数的优化模型，进而提取源域和目标域之间相关度最高的特征。

而边缘分布自适应是利用源域与目标域边缘概率分布之间的距离来近似两个领域之间的差异，即

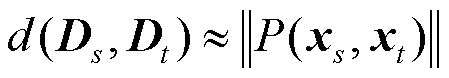
TCA通过构造最大均值差异(Maximum Mean Discrepancy, MMD)来衡量两个分布之间的相似程度。

3 暂态稳定评估模型构建

3.1 评估标准

电力系统暂态稳定评估是一类典型的非平衡分类[26]，对于失稳的漏判或误判显然要比保持稳定的误判带来的危害要大得多，采用单一的准确率标准评价模型性能不够客观，因此引入故障率指标综合评价TSA模型的评估性能。其中，暂态稳定评估的混淆矩阵如表1所示，TP、FN为稳定样本被正确或错误评估的数量，FP、TN为失稳样本被正确或错误评估的数目。

表1 混淆矩阵

根据混淆矩阵，可以采用以下4个指标来综合评估模型分类的性能。

第1个指标是准确率，代表分类器对测试样本分类的总体情况，表达式为

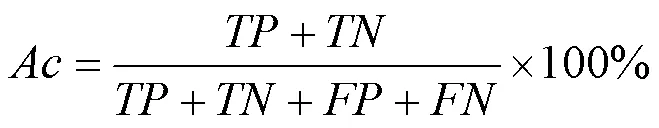
第2个指标是稳定样本查全率，指所有真实标签为稳定的样本中预测正确的比例，主要反映该分类器处理TSA问题时的安全性，表达式为

第3个指标是失稳样本查全率，指所有真实标签为失稳的样本中预测正确的比例，主要反映该分类器处理TSA问题时的可靠性，表达式为

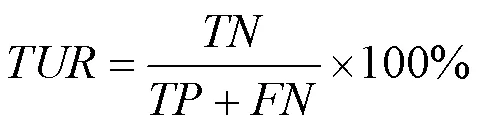
第4个指标是上述两个查全率的几何平均数，其表达式为

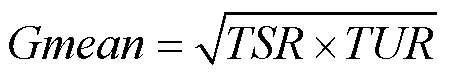
3.2 稳定判据

时域仿真法通过计算电力系统各电气量进行暂态稳定评估，稳定与否根据暂态稳定指数(Transient Stability Index, TSI)进行判断。

4 算例分析

4.1 数据构造

4.2 模型构建

本文选取样本故障前某一时刻、故障发生时刻以及故障切除时刻的数据，一共39条母线，取46条输电线路电压在故障前、故障中、故障后的电压数值和相角大小以及各线路潮流有功、无功功率大小作为输入特征，输入数据的维度为448维。集成学习与迁移学习算法均在开源机器学习库scikit-learn环境下进行，卷积神经网络等深度学习算法在Tensorflow环境下进行，编程语言为python，PC配置为Intel(R) Core(TM) i7-10875H CPU/16GB RAM。在集成学习模型中共使用了7种机器学习算法，分别为：支持向量机SVM，高斯核函数；K值近邻法KNN，近邻个数取10；人工神经网络ANN，取层数分别为80、10的两个隐藏层；随机森林RF，森林决策树数为10，寻找最佳分割时需要考虑的特征数目为3；梯度提升决策树GBDT，需要使用到的决策树的个数为100；Logistic算法正则化系数取0.01；Adaboost算法采用DT决策树集成，决策树个数为100。

为了得到最有效的集成方法，将7种集成学习算法得到的预测值作为训练集，得到6 530组7维特征的一组样本训练集。遍历7种算法以及以均值集成的8种模型，其中均值集成模型在表中用Mean表示，对其进行训练后，测试得到以8种方法进行集成的模型评估指标，如表2所示。

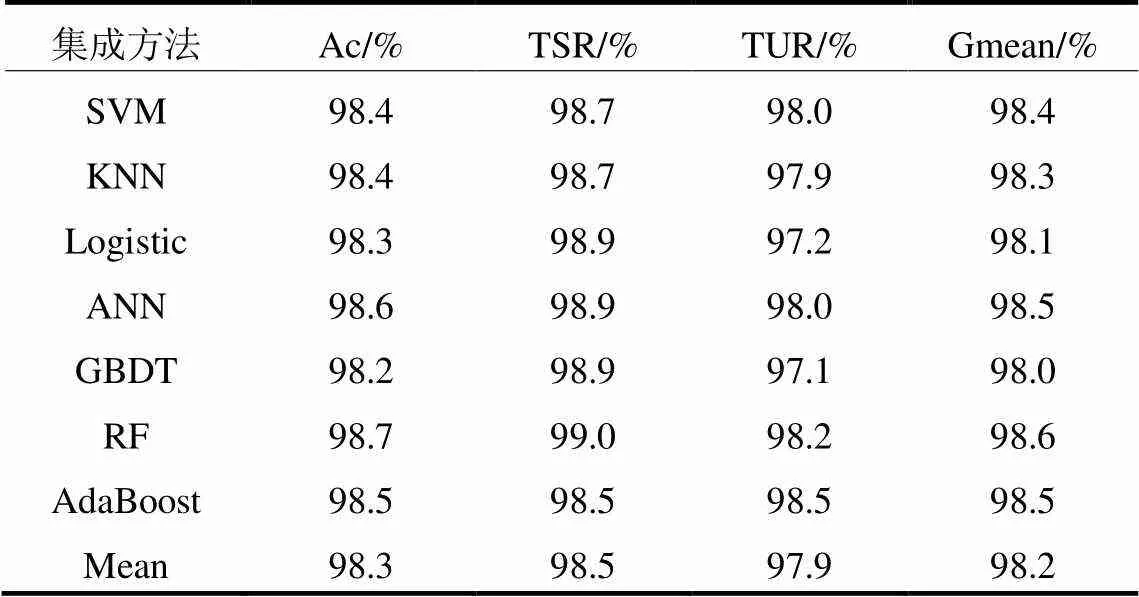
表2 不同集成方法的模型性能对比

从表2中可以发现，采取RF算法时性能最优。

对各种机器学习算法分别进行仿真，各模型的性能评估见图3。其中，用Ensemble代表利用RF集成多种学习器后,对同一测试集进行测试后的评价指标的值。

图3 各模型性能评估

从图3可以看出，RF集成学习模型的准确率Ac和安全性参数TSR均为最高，分别为98.74%，99.05%，其输出的混淆矩阵如图4所示。

图4 RF集成学习测试输出的混淆矩阵

在TSA中，安全性TSR参数的重要程度显然要高于可靠性TUR参数。所以，集成学习模型所表现出的性能明显高于未集成之前的各分类器模型。

本文将所提出的集成学习算法与深度学习算法CNN、SSAE进行比较，其中，CNN采用3个一维卷积层。卷积神经元个数为32、64、64，卷积核大小为6，训练周期为60，SSAE共两层，每层的隐含层数目为400、200，L1正则化系数为0.005、0.005，稀疏参数分别为0.15、0.05，训练周期为200。控制测试集和训练集的输入一致，分析了二者性能，如图5所示。

图5 集成学习与深度学习的性能对比

从图3、图5中可以看出，所提集成学习算法无论是在准确度还是安全性方面都优于深度学习算法。

表3将所提模型与深度学习模型CNN和SSAE的训练速度进行了对比。经过比较后发现，所提模型的训练速度更优，但预测单个样本时长稍长。

表3 模型用时对比

4.3 含噪声时的模型性能分析

实际系统运行过程中，数据在测量以及传输途中可能会产生误差，为了更好地模拟实际情况，本文通过向数据中添加符合高斯分布的噪声，具体添加方式如式(23)所示。

图6分别给出了集成学习模型以及参与集成的各分类器，在噪声环境下的准确率以及安全性参数值，其中RF、KNN算法在面对噪声时的性能较低，为清晰地显示集成学习算法的准确性，将图像适当纵向放大。

图6 模型抗干扰评估

从图6可以看出，集成学习对噪音的抗干扰能力更强，模型预测的准确性始终维持在98.4%以上，并且随着噪音的增大，两者性能之间的差别也逐渐增大。除了图中所出现的机器学习方法外，其余方法在噪音的干扰下精确度出现了较大程度的下降，尤其是KNN算法和RF算法的准确率分别下降为89.8%和95.2%。

表4给出了在考虑噪音时不同算法的抗干扰能力，可以看到通过本文所提方法集成之后各类算法的准确度都得到了明显的提高，当噪音较大时，Bagging集成学习和其他算法的差异也更加明显。

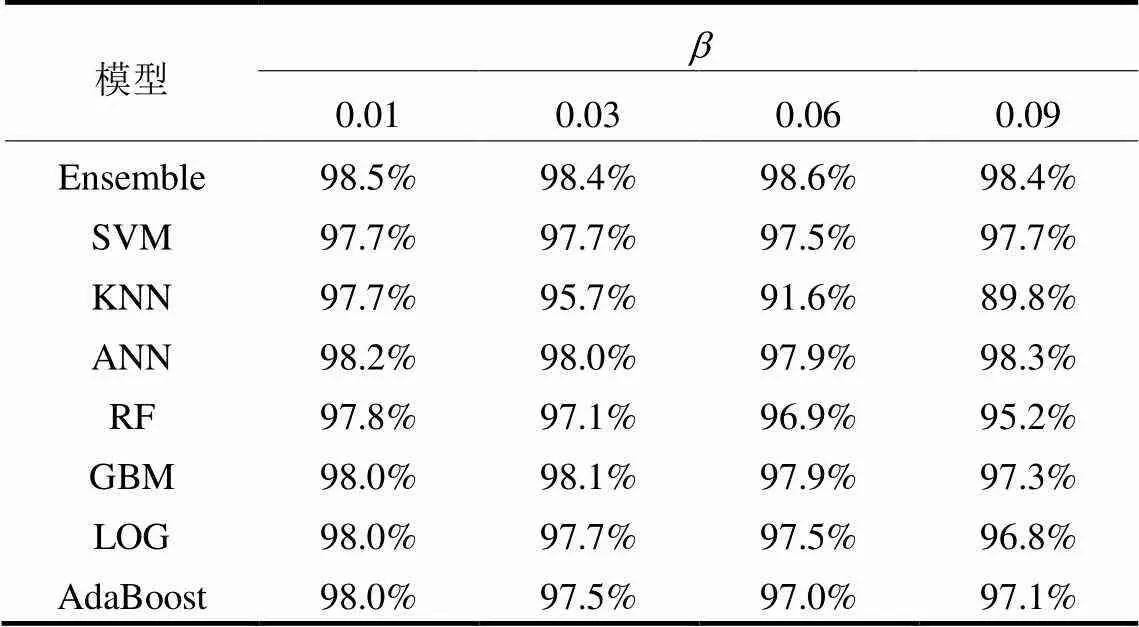
表4 含噪声时的模型性能对比

4.4 模型的在线更新

当系统母线9发生故障需要切除时，系统变更为38节点系统，并且线路数减少2条。IEEE10机39节点系统去掉第9条母线，与之相连的线路也一同缺失，38节点系统的拓扑结构如图7所示。新产生的数据与原先的数据维度不符，原有分类器不能对新拓扑结构下的系统进行暂态稳定评估。并且当系统拓扑结构发生改变后，没有足够的离线数据供分类器进行训练。因此需要充分挖掘原有39节点的数据来进行学习，才能满足在线更新的需求。

图7 IEEE10机38节点系统拓扑结构

4.4.1基于Boosting集成的样本迁移

通过Boosting集成的样本迁移思想，将拓扑结构改变后产生的数据作为辅助训练样本，将拓扑结构改变前的数据作为原训练样本，进行样本迁移，设置迭代次数为10，迭代算法为本文所建立的Bagging集成分类器，对测试样本进行测试。

4.4.2基于TCA的特征迁移

通过TCA算法，利用拓扑结构改变后产生的数据，与拓扑结构改变前的历史数据进行特征迁移，进而获得大量的仿真数据。本文采用的TCA方法取高斯核函数进行计算，核函数宽度为1，特征维度为30，对于偏移量不同的样本分别进行迁移，得到不同的样本集对模型进行训练，测试结果如图8所示。

图8 迁移学习模型性能评估

4.4.3测试结果

对失去一条母线38节点的模型进行同样类型的暂态稳定仿真，由于第8、9条线路以及一条母线的缺失，共得到了7 594组数据，且数据维度变为432，随机取出其中2 253组数据作为测试集，其余5 341组数据作为辅助训练集备用。将之前39节点仿真得到的8 788组数据作为原始样本集导入TrEnsemble模型，并取少量相对应的38节点训练集数据作为辅助样本集代入模型，将测试集导入训练后的模型进行测试，模型正确率随样本数量的增加而变化的曲线如图8中TrEnsemble所示；若将39节点数据集代入TCA进行特征提取，重复上述工作，得到正确率随样本数量的增加而变化的曲线如图8中TCA+Ensemble所示；而只将38节点的数据集作为训练集代入普通的Bagging集成算法进行训练测试，对应的结果如图8中Ensemble所示。

通过对比发现，TrEnsemble方法在只有少量训练样本集时展现出较高的预测精度，并且在训练样本增加的同时，精度也随之增加，而TCA法本质上是特征迁移方法，所以对训练样本大小其实并不敏感，其精度也基本保持稳定，两种方法均可适用于本文提出的暂态稳定评估模型的在线更新。

4.5 模型通用性分析

表5 IEEE16机68节点仿真结果

由表5中数据可知，本文方法在IEEE16机68节点算例下依旧保持最高的性能和精度，说明本文所提方法在不同的系统结构下也能保持良好的通用性。

5 结论

本文提出了一种多模态集成的Bagging集成学习算法，并将其引入电力系统的暂态稳定评估中，在IEEE10机39节点系统以及IEEE16机68节点系统上进行了仿真研究。

1) 区别于将多个相同模型进行加权平均的传统集成学习模型，本文将多个机器学习模型对应的预测值进行二次学习得到最后的预测结果。试验证明，所提模型在准确度和安全性指标上均优于各子机器学习模型以及传统深度学习模型。

2) 考虑噪声的影响，对原有测试集加入高斯噪声重复实验。结果表明，Bagging集成学习模型在各种噪声环境下均能保持较高的准确率，而其他机器学习模型则出现精度下降、性能降低等现象。

3) 当系统拓扑结构发生变化时，将所提模型与Boosting样本迁移学习算法思想和TCA特征迁移学习算法相结合。提出两种不同的暂态稳定模型在线更新方法，并与传统方法相比，证明所提算法能够适应暂态稳定评估模型的在线化更新。

[1] 孙华东, 许涛, 郭强, 等.英国“8·9”大停电事故分析及对中国电网的启示[J].中国电机工程学报, 2019, 39(21): 6183-6192.

SUN Huadong, XU Tao, GUO Qiang, et al.Analysis of "8·9" blackout accident in UK and its enlightenment to China's power grid[J].Proceedings of the CSEE, 2019, 39(21): 6183-6192.

[2] 朱朝阳.委内瑞拉大停电事故的背后[J].国家电网, 2019(5): 72-74.

ZHU Chaoyang.Behind the blackout in Venezuela[J].State Grid, 2019(5): 72-74.

[3] 易俊, 卜广全, 郭强, 等.巴西“3·21”大停电事故分析及对中国电网的启示[J].电力系统自动化, 2019, 43(2): 1-6.

YI Jun, PU Guangquan, GUO Qiang, et al.Analysis of the "March 21" blackout accident in Brazil and its enlightenment to China's power grid[J].Automation of Electric Power Systems, 2019, 43(2): 1-6.

[4] 王毅星.基于深度学习和迁移学习的电力数据挖掘技术研究[D].杭州: 浙江大学, 2019.

WANG Yixing.Power data mining technology based on deep learning and transfer learning[D].Hangzhou: Zhejiang University, 2019.

[5] CHAO Ren, XU Yan, ZHANG Yuchen.Post-disturbance transient stability assessment of power systems towards optimal accuracy-speed tradeoff[J].Protection and Control of Modern Power Systems, 2018, 3(1): 1-10.

[6] WU Shuang, ZHENG Le, HU Wei, et al.Improved deep belief network and model interpretation method for power system transient stability assessment[J].Journal of Modern Power Systems and Clean Energy, 2020, 8(1): 27-37.

[7] 王亮, 韩冬, 王长江, 等.基于MVEE和LSPTSVM的电力系统暂态稳定评估[J].电力系统保护与控制, 2020, 48(17): 45-54.

WANG Liang, HAN Dong, WANG Changjiang, et al.Power system transient stability assessment based on MVEE and LSPTSVM[J].Power System Protection and Control, 2020, 48(17): 45-54.

[8] 田芳, 周孝信, 于之虹.基于支持向量机综合分类模型和关键样本集的电力系统暂态稳定评估[J].电力系统保护与控制, 2017, 45(22): 1-8.

TIAN Fang, ZHOU Xiaoxin, YU Zhihong.Power system transient stability assessment based on comprehensive SVM classification model and key sample set[J].Power System Protection and Control, 2017, 45(22): 1-8.

[9] 张春.基于关联规则的电力系统暂态稳定评估方法研究[D].北京: 华北电力大学, 2017.

ZHANG Chun.Study on transient stability assessment method based on association rules[D].Beijing: North China Electric Power University, 2017.

[10] 王胜, 冯兴明, 周宇, 等.基于BP神经网络预测的微网系统dq轴谐波阻抗的主动测量策略[J].电测与仪表, 2021, 58(3): 118-125.

WANG Sheng, FENG Xingming, ZHOU Yu, et al.An active measurement strategy of dq-axis harmonic impedance in micro-grid system based on BP neural network prediction[J].Electrical Measurement & Instrumentation, 2021, 58(3): 118-125.

[11] MADHIARASAN M.Accurate prediction of different forecast horizons wind speed using a recursive radial basis function neural network[J].Protection and Control of Modern Power Systems, 2020, 5(3): 48-56.

[12] 刘谋海, 胡军华, 丁国栋, 等.基于深度学习的电力监控视频超分辨率重建[J].电力系统保护与控制, 2021, 49(11): 181-187.

LIU Mouhai, HU Junhua, DING Guodong, et al.Super-resolution reconstruction of a power monitoring video based on deep learning[J].Power System Protection and Control, 2021, 49(11): 181-187.

[13] 郑炜, 林瑞全, 王俊, 等.基于GAF与卷积神经网络的电能质量扰动分类[J].电力系统保护与控制, 2021, 49(11): 97-104.

ZHENG Wei, LIN Ruiquan, WANG Jun, et al.Power quality disturbance classification based on GAF and a convolutional neural network[[J].Power System Protection and Control, 2021, 49(11): 97-104.

[14] 田芳, 周孝信, 史东宇, 等.基于卷积神经网络的电力系统暂态稳定预防控制方法[J].电力系统保护与控制, 2020, 48(18): 1-8.

TIAN Fang, ZHOU Xiaoxin, SHI Dongyu, et al.A preventive control method of power system transient stability based on a convolutional neural network[J].Power System Protection and Control, 2020, 48(18): 1-8.

[15] 王怀远, 陈启凡.基于堆叠变分自动编码器的电力系统暂态稳定评估方法[J].电力自动化设备, 2019, 39(12): 134-139.

WANG Huaiyuan, CHEN Qifan.Power system transient stability assessment method based on stacked variational autoencoder[J].Electric Power Automation Equipment, 2019, 39(12): 134-139.

[16] SANER C B, YASLAN Y, GENC I.An ensemble model for wide-area measurement-based transient stability assessment in power systems[J].Electrical Engineering, 2021, 103: 2855-2869.

[17]李扬, 李国庆, 顾雪平, 等.基于集成OS-ELM的暂态稳定评估方法[J].电工技术学报, 2015, 30(14): 412-418.

LI Yang, LI Guoqing, GUO Xueping, et al.Transient stability assessment of power systems based on ensemble OS-ELM[J].Transactions of China Electrotechnical Society, 2015, 30(14): 412-418.

[18] HAMDI H, REGAYA C B, ZAAFOURI A.A sliding-neural network control of induction-motor-pump supplied by photovoltaic generator[J].Protection and Control of Modern Power Systems, 2019, 4(4): 306-322.

[19] LIU Songkai, LIU Lihuang, FANG Youping, et al.An integrated scheme for online dynamic security assessment based on partial mutual information and iterated random forest[J].IEEE Transactions on Smart Grid, 2020, 11(4): 3606-3619.

[20] 李宝琴, 吴俊勇, 邵美阳, 等.基于集成深度置信网络的精细化电力系统暂态稳定评估[J].电力系统自动化, 2020, 44(6): 17-26.

LI Baoqin, WU Junyong, SHAO Meiyang, et al.Refined transient stability assessment of power system based on integrated deep confidence network[J].Automation of Electric Power Systems, 2020, 44(6): 17-26.

[21] 史佳琪, 张建华.基于多模型融合Stacking集成学习方式的负荷预测方法[J].中国电机工程学报, 2019, 39(14): 4032-4042.

SHI Jiaqi, ZHANG Jianhua.Load forecasting based on multi-model by Stacking ensemble learning[J].Proceedings of the CSEE, 2019, 39(14): 4032-4042.

[22] 杜涵潇, 汤旻安.基于CEEMD-RSVPSO-KELM的用户侧微电网短期负荷预测[J].电测与仪表, 2020, 57(18): 69-76.

DU Hanxiao, TANG Min’an.Short-term load forecasting for user-side micro-grid based on CEEMD-RSVPSO- KELM model[J].Electrical Measurement & Instrumentation, 2020, 57(18): 69-76.

[23] 戴文渊.基于实例和特征的迁移学习算法研究[D].上海: 上海交通大学, 2008.

DAI Wenyuan.Instance-based and feature-based transfer learning[D].Shanghai: Shanghai Jiao Tong University, 2008.

[24] PAN S J, WSANG I W, KWOK J T, et al.Domain adaptation via transfer component analysis[J].IEEE Transactions on Neural Networks, 2011, 22(2): 199-210.

[25] 张倩, 李海港, 李明程, 等.基于多源动态TrAdaBoost的实例迁移学习方法[J].中国矿业大学学报, 2014, 43(4): 713-720.

ZHANG Qian, LI Haigang, LI Mingcheng, et al.Instance transfer learning method based on multi-source dynamic Tradaboost[J].Journal of China University of Mining and Technology, 2014, 43(4): 713-720.

[26] WANG Huaiyuan, WANG Qingyin, CHEN Qifan.Transient stability assessment model with improved cost-sensitive method based on the fault severity[J].IET Generation, Transmission & Distribution, 2020, 14(20): 4605-4611.

On-line transient stability assessment of a power system based on Bagging ensemble learning

ZHAO Dongmei1, XIE Jiakang1, WANG Chuang1, WANG Haoxiang1, JIANG Wei2, WANG Yi1

(1.School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China;2.China Huaneng North Weijiamao Power and Coal Co., Ltd., Erdos 010308, China)

To solve the problems of poor stability and low accuracy of traditional machine learning in transient stability assessment and the limitations of offline training, an online transient stability assessment model based on multi-model fusion Bagging ensemble learning method is proposed.First, in combination with research on the frontier theory of artificial intelligence, the principles and implement methods of seven machine learning algorithms commonly used in transient stability assessment are analyzed, and the Bagging method is used to integrate them to give full play to the advantages of each model.Secondly, the mathematical method of Bagging ensemble learning is given and a simulation experiment is carried out.When the topological structure of the original system changes, a Boosting algorithm and transfer component analysis are used to carry out sample and feature transfer of the original grid historical data to complete the online update of the proposed model.IEEE10-machine 39-bus system and IEEE16-machine 68-bus system are used in the simulation analysis, and the results show that the proposed method is more accurate than the traditional machine learning model.It can maintain stable operation when the data is mixed with noise, and accurately evaluate transient stability by transferring the historical data when the system topology changes.

Bagging ensemble learning; power system; machine learning; transient stability; transfer learning; on-line updating

10.19783/j.cnki.pspc.210817

2021-07-03；

2021-08-25

赵冬梅(1965—)，女，博士，教授，研究方向为电力系统分析与控制、新能源发电与智能电网；E-mail: zhao-dm@ ncepu.edu.cn

谢家康(1998—)，男，通信作者，硕士研究生，研究方向为电力系统分析、机器学习；E-mail: 1354667160@qq.com

王 闯(1997—)，男，硕士研究生，研究方向为电力系统分析、机器学习。E-mail: wangchuang@ncepu.edu.cn

国家重点研发计划项目资助(2017YFB0902600)；国家电网公司科技项目资助(SGJS0000DKJS1700840)

This work is supported by the National Key Research and Development Program of China (No.2017YFB0902600).

(编辑 许 威)