测量施力对卡尺测量精度的影响研究

董中新

桂林广陆数字测控有限公司

1 引言

卡尺是广泛应用于机械制造业的重要手持测量工具，对生产现场的零部件测量和质量保障有重要意义。卡尺结构特点和测量方式是尺框在尺身上作相对移动，通过数显装置、游标或指示表显示尺框和尺身上两量爪之间的平行间距，达到测量距离的目的。根据上述三种测量方式，可分为数显卡尺、游标卡尺和带表卡尺三种类型。随着时代和技术的发展，卡尺量具不仅应用于手动测量场合，也逐步应用在基于物联网的测量和质量监控领域[1]。

影响卡尺测量精度因素有很多，包括制造误差、结构间隙和显示单元等卡尺本身误差，而且与环境条件、操作状况以及多种偶然因素相关，其中，操作状况主要涉及测量操作过程的测量力。针对上述各种影响因素及其影响关系已有较多研究和文献介绍，如针对检定环节的卡尺检定不确定度评定方法[2]、针对使用环节的卡尺测量误差来源和不确定度分析[3-5]等。

卡尺属于接触式测量器具，在测量过程存在测量力，因而会影响测量结果，通过实践考察和研究可知，此影响较为明显。文献[3-5]论述了测量力对测量精度的影响，其中文献[3，4]涉及到测量力影响测量结果的简化分析计算；文献[6]定性讨论了量爪碰伤变形引起的测量误差。现有研究认为，测量力对精度的影响主要包括尺身弯曲变形和量爪变形，但进一步分析发现，测量力实际影响还应包括卡尺量爪与测量对象的接触变形及工件自身变形。由于卡尺主要零件形状结构很不规则，基于简化力学计算方法的研究具有局限性，并且人工测量过程中，测量力还因人因时而异。因此，基于有限元方法进一步分析研究测量力对测量状态和结果的整体影响具有重要意义。

2 测量力对卡尺测量状态的影响

测量力对测量状态影响的本质是导致卡尺产生相对变形、位移和应力，继而产生相应的测量误差。此外，卡尺零件应力对卡尺使用寿命也有一定影响，特别是存在频繁且较大的测量力作用时。

如图1所示，将卡尺和测量对象(即测量工件)作为整体考虑，其中x为测量长度，y为测量高度(即测量点至尺身长杆下边沿的距离)。测量过程中，手握力固定尺身，在测量力Fa作用下，量爪和工件之间产生作用力和反作用力，记为Fz。这一相互作用力使卡尺产生弯曲变形和接触变形，也使工件产生变形。忽略摩擦力的影响，根据力的平衡有Fz=Fa。

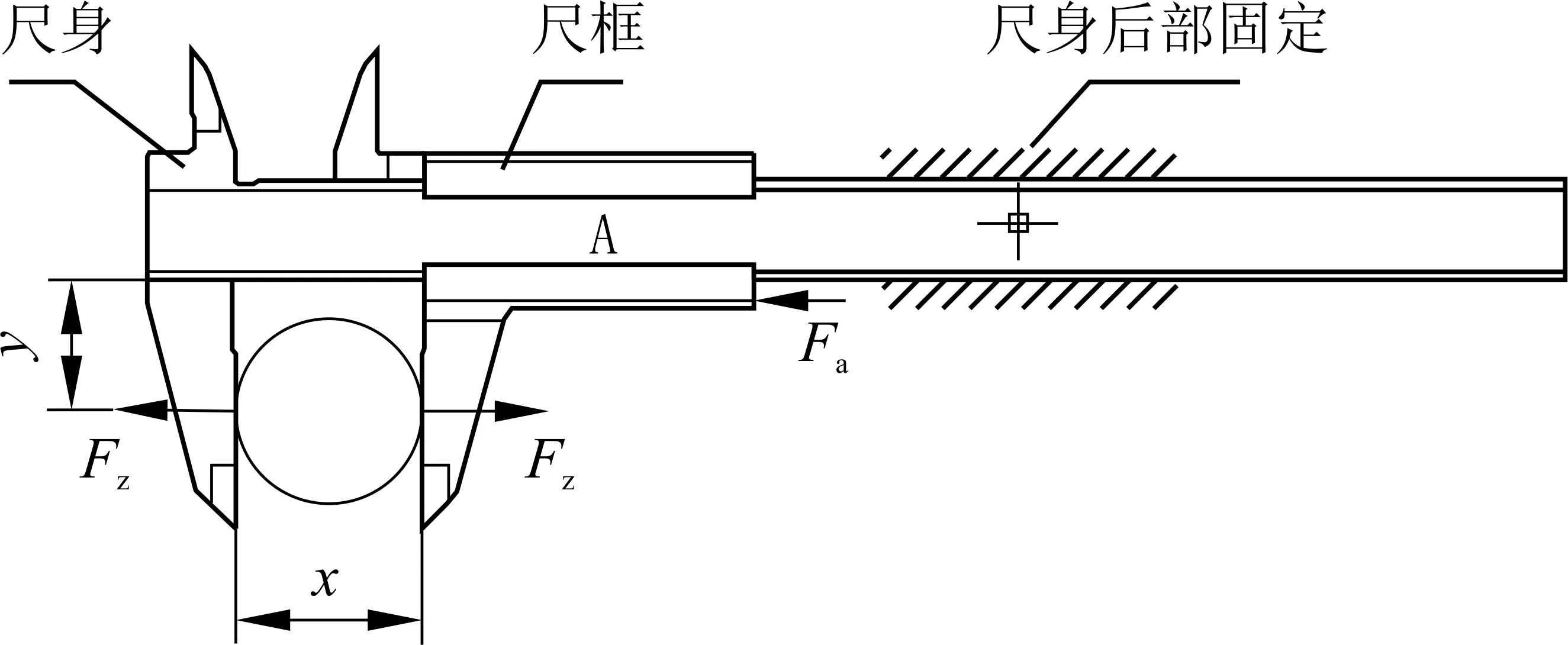
图1 卡尺测量力

2.1 测量力引起的卡尺测量误差影响分析

根据图1所示作用关系，测量力影响测量结果导致各部分产生变形和位移原因如下。

(1)尺身弯曲变形引起的测量误差

如图2所示，在相互作用力下，尺身产生弯曲变形导致尺身量爪倾斜变形，尺框与尺身发生相对移动，产生测量误差，记为Δ1。

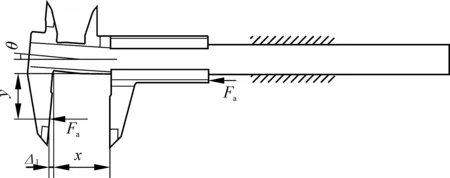
图2 测量力引起的尺身弯曲变形

(2)量爪弯曲变形引起的测量误差

如图3所示，在相互作用力下，两边量爪产生弯曲变形，从而引起尺框与尺身相对移动，产生测量误差，记为Δ2。

图3 测量力引起的量爪弯曲变形

(3)工件自身变形及接触变形引起的测量误差

在相互作用力下，工件受到压力产生变形，工件与量爪接触处产生接触变形，总变形为Δ3，从而引起尺框与尺身的相对位移，移动量即为Δ3。Δ3与工件自身刚度和测量接触处的接触刚度有关，即与工件形状、尺寸和材料有关。

还有其它影响环节，如尺框扭转变形，但此变形较小，且转换为测量方向的误差更为微小，可忽略。

因此在测量力作用下，引起的测量总误差为

Δa=Δ1+Δ2+Δ3

(1)

式中，Δa为测量力引起的测量误差总和。

2.2 测量力引起的测量误差计算

作为卡尺的主要零件，尺框和尺身均为较复杂的异形零件，进行变形计算需采用简化形式。

(1)Δ1近似计算

如图2所示，根据材料力学[7]，有

(2)

式中，θ为测量力作用下尺身的弯曲偏角；M1为测量力对尺身产生的弯矩；E为材料弹性模量；I1为尺身长杆的截面惯性矩。

因变形相对于结构尺寸很小，近似计算测量误差Δ1得

(3)

(2)Δ2近似计算

如图3所示，根据材料力学，有

(4)

式中，I2为量爪在y范围内的当量截面惯性矩。因为量爪沿y向为不规则形状，各处截面惯性矩不同，因而采用当量惯性矩。

(3)Δ3计算

Δ3与工件形状、尺寸和材料有关。以较常见的圆柱工件为例，根据弹性接触力学理论[8]，得

(5)

式中，R为测量工件的半径；H为工件厚度。为方便计算，假设工件厚度与量爪厚度相同，并假定量爪和工件材料的弹性模量、泊松比相等。

以相同材料的圆柱工件为例，测量力引起的测量误差计算式为

(6)

式中，Δa与Fa，R，y均为非线性递增关系；由于Δ3相对较小，可忽略，则Δa与Fa，R(或x)为线性递增关系。由于I2计算相当麻烦，可按近似当量值计算。

3 测量力对测量状态的影响有限元分析

式(6)为测量力对卡尺测量误差的影响关系，但具体计算涉及量爪当量截面惯性矩的确定，计算并不方便，因此采用细分网格的有限元分析方法更为有效。

3.1 有限元分析模型

采用最常用的0～150mm规格游标卡尺为例，测量对象为常规钢质圆柱体，半径R分别为7.5mm和25mm。根据实际测量状况，卡尺测量过程的状态约束模式如下：

(1)尺身后部固定，尺框在测量力作用下移动并使量爪与工件接触；

(2)尺框与尺身之间两侧和上下部均约束。

卡尺和工件材料的弹性模量E=2.06×105MPa，泊松比μ=0.3，测量施力Fa取5N，10N，20N，30N，40N。采用实体SOLID185单元进行网格划分，网格单元为四面体，边长为1mm，网格划分见图4。

图4 卡尺有限元分析网格划分

3.2 有限元分析结果

由于尺身后部固定，因此尺框下部中点A(见图1)的形变为尺框与尺身的相对位移量，记为δa，即为有限元分析得出的测量误差。根据有限元法分析结果得到δa-Fa关系(见图5)。

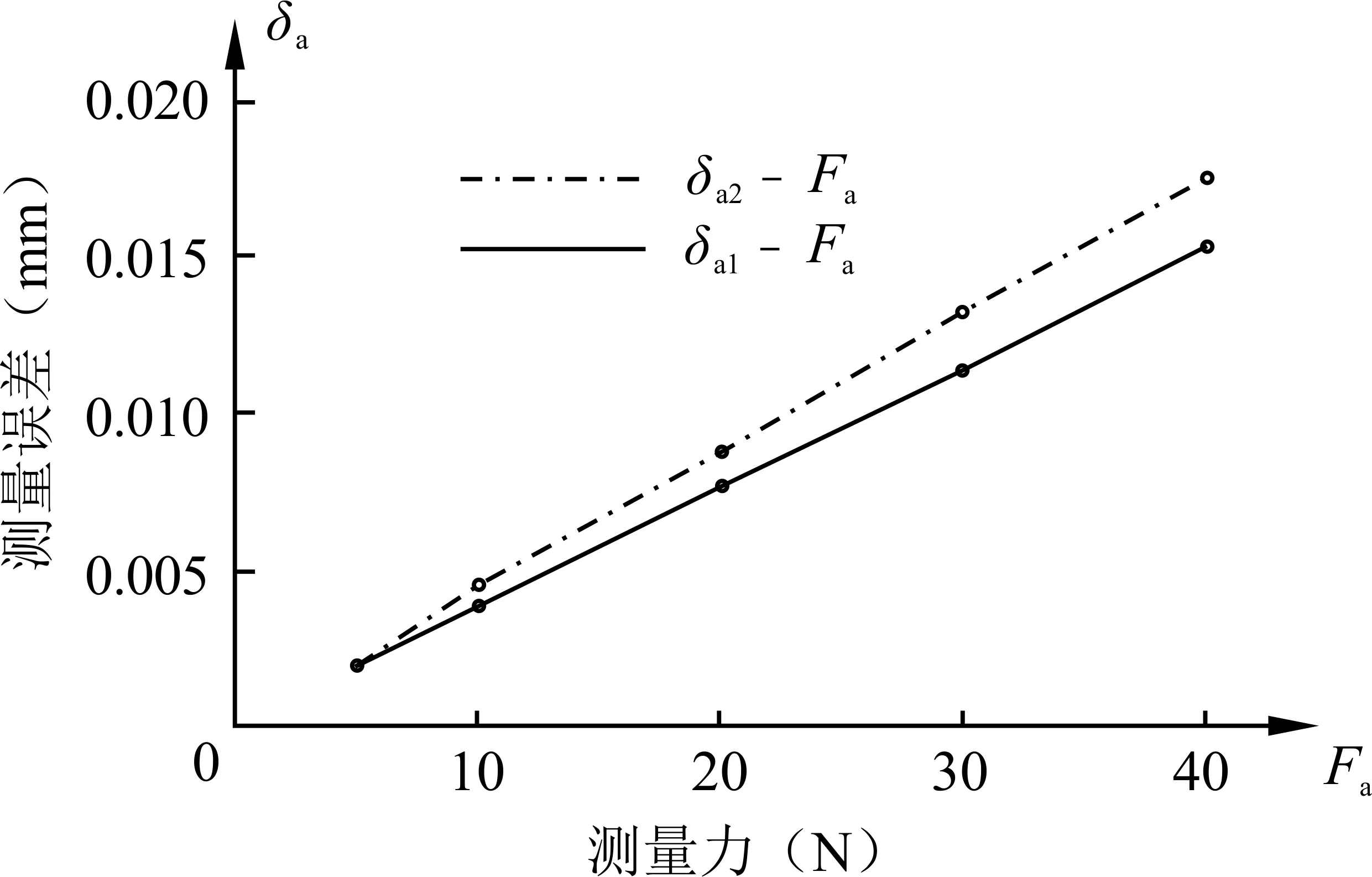
图5 基于有限元法的测量误差与施力关系

测量对象圆柱半径7.5mm和25mm对应的分析测量误差分别为δa1，δa2。可以看出，测量误差δa1，δa2与测量施力Fa近似为线性递增关系，符合式(6)推论。

可以对其它规格和形状的钢质测量工件进行同样的有限元分析，也可以参照上述两个关系作线性插值处理而近似确定。

4 结果分析

根据式(6)和有限元分析结果，关于测量施力产生的测量误差关系以及改进措施有如下结论。

(1)测量力对测量误差的影响关系

①测量误差Δa(δa)与测量力Fa为非线性递增关系，在本例中，Δ3相对很小，可忽略，此时测量误差Δa与测量力Fa近似为线性递增关系。此情况可近似适用于工件自身刚度较高的测量场合，若工件自身刚性较弱，则Δ3较大。

②在误差构成中，量爪变形Δ2较大，且与测量长度x无关。尺身弯曲引起的变形Δ1与x近似为线性递增关系，当x较小时，Δ1相对Δ2较小。

③Δ1和Δ2与测量高度y分别为二次方和三次方递增关系，因此y的影响很大。

④由于分析过程假设尺身与尺框之间的约束为理想约束，但实际上两者之间有弹性约束，因此实际误差比分析误差略大。

⑤根据分析，在工件刚度较高(如钢质工件)的场合，当测量力约达到10N后测量误差较大，明显影响测量精度；一般测量力应控制在约5N内，此时测量误差约0.002mm，考虑存在摩擦力，测量力可略微增大；在特殊情况下，如测量精度要求不高时，可允许适当加大测量力。

(2)改进方向

根据上述分析和结论可知，从测量方式和卡尺结构来看，减小因测量力而产生的测量误差措施有：①在测量可靠前提下应尽量减小测量高度y。②在保证合理外形和轻量化以及美观要求前提下，适当增大结构尺寸，特别是适当增大量爪宽度，以提高截面惯性矩I1和I2。

手持卡尺测量工件时，应适当施加测量力，保证卡尺和工件测量处可靠接触，但测量力过大会产生较大的测量误差，明显降低测量精度，因此测量施力需控制适当。

5 结语

卡尺为机械制造业常用的、重要的现场测量工具，测量时需施加一定的测量力，以保证可靠的测量接触，但测量施力过大会导致尺身、量爪和工件发生较大变形，从而产生较大测量误差，明显影响测量精度。

通过理论分析和有限元法分析可得出，测量误差与测量力为非线性递增关系，在工件刚度较大时，可近似为线性关系。为减小测量误差，在保证测量接触可靠的前提下，测量施力和测量高度应尽可能小；当工件自身刚度较高时，一般测量力应控制在约5N内，此时测量误差约在0.002mm以内，考虑存在摩擦力，测量力可略微增大。