参数失配LCL 型并网逆变器模型预测控制方法研究
2022-04-19朱子林武对娣
龙 波,朱子林,洪 敏,武对娣,廖 勇
(1.电子科技大学机械与电气工程学院,成都 611731;2.电子科技大学电动汽车动力系统与安全技术研究所,成都 611731;3.浙江运达风电股份有限公司,杭州 310012)
随着可再生能源分布式发电系统RE-DPGS(renewable energy-distributed power generation sys-tem)的发展,三相电压源型逆变器得到了更为广泛的应用[1]。逆变器是连接RE-DPGS 与电网的枢纽,其性能直接影响电能的质量,所以对逆变器的控制策略研究势在必行[2]。在数字信号处理器DSP(digital signal processor)高速发展的背景下,模型预测控制MPC(model predictive control)凭借其优良的离散控制特性被广泛应用于电力电子领域[3]。传统MPC 仅对机侧电流进行控制[4],通过控制机侧电流来间接控制网侧电流,故网侧电流质量有待提高。新型MPC 对机侧电流、网侧电流、滤波电容电压均可进行控制,并网电流质量相较于传统MPC 控制方法有显著提高。在实际工况运行中,电路中的电感、电容等参数会随着温度、磁路等变化而波动,而MPC 的控制效果依赖精确的数学模型,当标称值与工作值存在误差时,会造成参数失配,影响逆变器的控制性能[5-6]。
针对MPC 参数摄动问题,国内外学者提出了很多解决方法。文献[7-8]分析了电感参数值失配对MPC 控制效果的影响;文献[9]对电感失配时的预测误差进行了理论分析;文献[10]提出一种自适应参考模型预测控制,通过多输入多输出模型构造虚拟参考值,提高系统的鲁棒性,但是该策略实现复杂;文献[11-12]将参数失配视为一种扰动,通过建立扰动观测器来增强控制系统的鲁棒性,然而该观测器的设计复杂,计算量大;文献[13]采用电网电压定向控制,利用系统的无功分量与电感之间的关系搭建电感观测器,并加入低通滤波器以消除辨识结果中的高频分量,有效增强控制器的参数鲁棒性,但是该电感观测器仅适用于定频式的预测控制策略;文献[14]根据电网电压幅值不变构建电感观测器,原理简单,但是该电感观测器的估计关系式复杂;文献[15-16]利用预测电流变化量与实际电流变化量之间的关系建立电感观测器,对预测模型进行实时修正,然而预测电流本就是估计值,使得观测结果有一定误差;文献[17]根据实际电压和电流之间的关系建立电感观测器,对模型进行实时修正,实现简单,鲁棒性好。
LCL 型滤波器相较于L 型滤波器体积更小,重量更轻,高频谐波衰减和低频谐波增益效果更好,目前LCL 滤波器应用更为广泛。本文提出一种LCL型并网逆变器的参数摄动模型预测控制方法。以机侧电流、网侧电流、滤波电容电压、开关频率为约束目标,采用试验法选取合适的权重因子实现权重分配,然后对目标函数进行约束控制,针对参数摄动引起的模型失配问题,建立参数观测器对电感和电容进行在线观测,以提高控制系统在参数摄动情况下模型预测控制的鲁棒性。
1 LCL 型并网逆变器模型预测控制策略
1.1 LCL 型并网逆变器数学模型
三相LCL 型并网逆变器拓扑如图1 所示,图中:Udc为直流电源;uinva、uinvb、uinvc为逆变器三相输出电压;uca、ucb、ucc为三相滤波电容电压;ea、eb、ec为电网电压;i1a、i1b、i1c为机侧三相电流;i2a、i2b、i2c为网侧三相电流;L1a、L1b、L1c为机侧滤波电感;R1a、R1b、R1c分别为L1a、L1b、L1c的寄生电阻;L2a、L2b、L2c为网侧滤波电感;R2a、R2b、R2c为L2a、L2b、L2c的寄生电阻;C 为滤波电容。
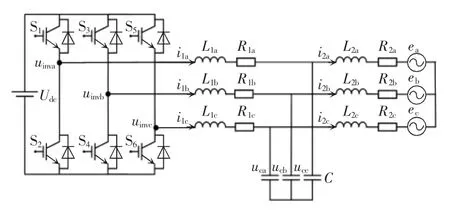
图1 三相LCL 型并网逆变器拓扑Fig.1 Topology of three-phase LCL-type grid-connected inverter
由基尔霍夫定律可得LCL 型并网逆变器的数学模型,将其进行Clark 变换得

式中:R1=R1a=R1a,L1=L1a=L1b=L1c,L2=L2a=L2b=L2c,uinv_αβ、i1_αβ为uinva、uinvb、uinvc和i1a、i1b、i1c分别在αβ 坐标系下逆变器的输出电压和输出电流;uc_αβ为滤波电容电压uca、ucb、ucc在αβ 坐标系下的值;i2_αβ为网 侧电流i2a、i2b、i2c在αβ 坐标系下的值;eαβ为电网电压ea、eb、ec在αβ 坐标系下的电压。
1.2 方案构成及工作原理描述
LCL 型并网逆变器的MPC 方案如图2 所示,令i1=[i1ai1bi1c]T,i2=[i2ai2bi2c]T,eg=[eaebec]T,uc=[ucaucbucc]T。图2 可大致分为功率模块、采样模块、MPC 预测模型、目标函数、观测器,其中:功率模块由三相逆变器的整流桥和LCL 滤波器组成;采样模块是将采样当前时刻状态值送入控制器进行处理;MPC 预测模型的作用是根据当前时刻状态预测下一时刻8 种状态;目标函数是由预测值和参考值的最小误差挑选最优开关序列;观测器的作用是估计电容和电感。

图2 LCL 型并网逆变器MPC 方案Fig.2 MPC scheme for LCL-type grid-connected converter
工作原理如下:
(1)采样当前时刻机侧电流i1、网侧电流i2、电容电压uc和电网电压eg,然后将上述状态值进行Clark 变换,送入MPC 预测模型进行计算;
(2)从预测模型得到预测值,经Park 变换后送入目标函数中;
(3)将dq 坐标系下的参考值送入目标函数,需要注意的是,机侧参考电流叠加了高频电容电压分量,是为了实现有源阻尼谐波谐振抑制;
(4)由目标函数挑选出使目标函数值最小的预测值对应的最优开关序列直接作用于电力开关器件;
(5)将观测器中的数值实时送入预测模型,提高参数摄动情况下并网逆变器的稳定性。
1.3 LCL 型并网逆变器MPC 预测模型
为降低开关损耗,提高逆变器转换效率,本文在目标函数中对电力开关器件的开关频率进行约束。此外,针对参数摄动的问题,提出了一种具有参数观测器的并网逆变器MPC 控制方法。
预测模型需要进行离散化处理,常用的离散化方法有前向差分法和后向差分法。
前向差分法离散化公式为

后向差分法离散化公式为

式(1)采用前向差分法离散化可得i1预测模型为

式中,uinv_αβ(k)为逆变器k 时刻输出的电压矢量。在每一个采样周期将8 种逆变器输出电压矢量依次代入式(8),通过目标函数选取与参考值最接近的预测值所对应的开关状态矢量在下一时刻作用于电力开关器件。逆变器输出电压矢量和开关状态矢量对应关系如表1 所示。
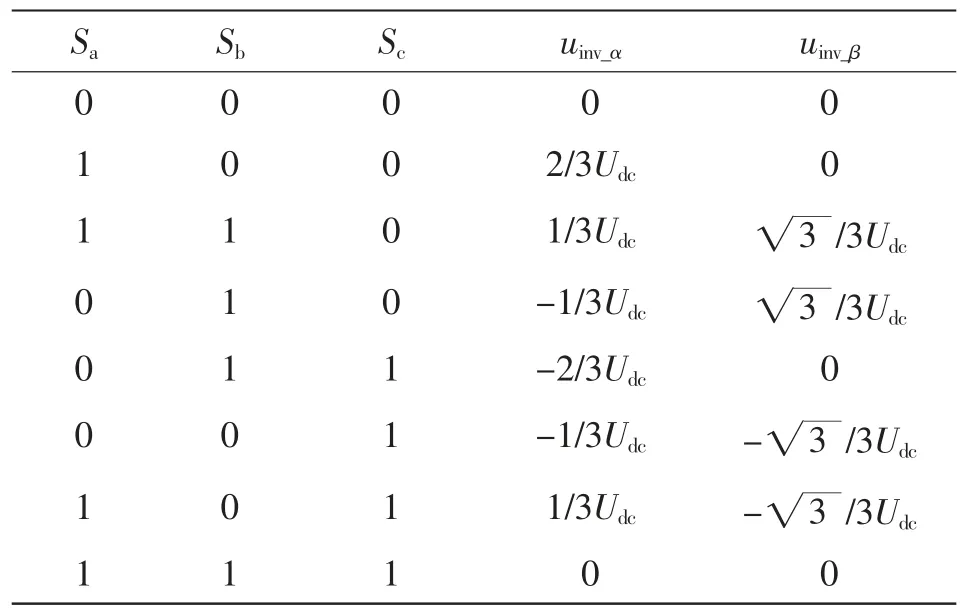
表1 开关状态与逆变器输出电压矢量对应关系Tab.1 Correspondence relationship between switching states and inverter output voltage vectors
式(1)和式(2)经后向差分法离散,并向前移动一步,消去uc(k+1)可得i2预测模型为
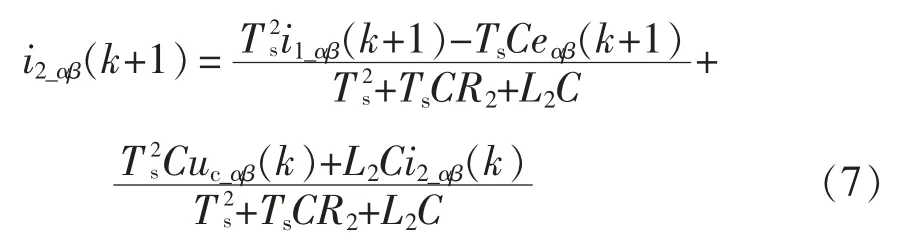
式(1)和式(3)经后向差分法离散,并向前移动一步,消去i2(k+1)可得uc预测模型为

这样两电平三相逆变器的8 种开关状态所对应的逆变器输出电压就决定了3 个预测模型的预测值。式(8)中eαβ(k+1)估计方法如下:在开关周期选取较小的情况下,eαβ(k+1)可估计为

式中,ω 为eαβ(k+1)的角频率。
将上述预测模型整理成状态空间表达式,则预测模型可以表示为

式中:x(k)=[i1_αβ(k)i2_αβ(k)ic_αβ(k)]T;

理论上,单步预测能够确保所选开关组合在一个控制周期的最优,但是在实际运行中,电流信号采样、电压信号采样和DSP 的控制与运算都需要一定的处理时间,尤其是对于高采样频率的控制系统而言,这就会导致最优开关序列的选取出现延迟,造成并网电流的相位滞后电网电压的现象,影响逆变器的功率因数。为补偿延迟,采用两步预测,在k 时刻对两个控制周期后的控制目标进行预测,x(k+2)为
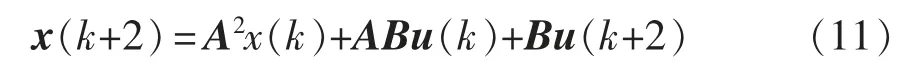
式中:u(k+2)的eαβ(k+2)可由式(9)迭代一次求得;uinv_αβ(k+1)为k+1 时刻逆变器输出电压。

为了对LCL 型逆变器谐振频率处的谐波进行抑制,采用电容电压比例反馈的有源阻尼策略。令为滤波电容电压高频分量,KC为有源阻尼反馈系数,KC=,一般取ζ 为0.7[18],则机侧电流参考值可选取为

因为采样时间Ts很小,而且两相旋转坐标系下各参考值的d 轴和q 轴分量为稳定常数,故可以将k 时刻参考值近似视为k+2 时刻参考值,即
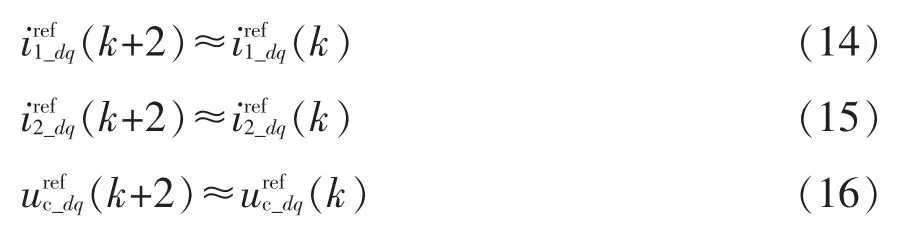
定义目标函数g 为

式中,λ 为各部分的权重因子,取λi1=10、λi2=10、λuc=1、λs=0.5。
2 模型误差对网侧预测电流的影响
LCL 滤波器位于逆变器功率电路的输出侧,滤波电容和滤波电感承载着的大电流和电压和较大的电流和电压变化率,易导致电容和电感本身会出现较大的温升。严重时会导致电感和电容参数值出现30%左右的摄动。然而在不考虑参数摄动的预测模型中标称值是固定的,当预测模型中的标称值和电路中的工作值失配时,会导致预测模型中的预测值不准确,影响控制效果。将机侧电感、网侧电感、电容的工作值代入式(7)中,得到

将式(7)与式(18)作差得网侧电流预测误差为

由于式(7)和式(18)分母不同,无法进行化简,故整理成式(19)的形式,从式(19)中可以看出,网侧预测电流误差和电感变化量、电容变化量、当前时刻的网侧电流、机侧电流、电容电压有关。
通过Matlab/Simulink 分析预测模型中参数L1、L2、C 变化对并网电流的影响,取L1=L2=5.0 mH,C=3.0 μF,考虑实际过程中电容和电感值可能存在50%参数变化,第1 组变化参数为L1=L2=2.5 mH,C=1.5 μF;第2 组变化参数为L1=L2=7.5 mH,C=4.5 μF。仿真结果分别如图3 和图4 所示。

图3 第1 组变化参数值的误差Fig.3 Errors of parameter variations in the first group


图4 第二组变化参数值的误差Fig.4 Errors of parameter variations in the second group
从图3 中可以看出,网侧电流误差为0.5 A,误差为3%;从图4 中可以看出,网侧电流误差为1.2 A,误差为6%;两组仿真在相位为π 及其整数倍时,网侧预测电流为0,可以看成极点,误差比值在极点处存在一个剧烈的抖动。此外,两组仿真证明了不同标称值对网侧预测电流会产生不同的影响,而该参数误差会导致预测电流产生误差,使得MPC 电流跟踪效果下降,所以要对电路中的电容和电感予以观测,提高系统的鲁棒性。
3 参数观测器及其设计
上一节简单分析了标称值变化对网侧预测电流的影响,本节通过建立参数观测器来实时观测电容和电感,实时更新预测模型的参数,提高控制系统的鲁棒性。
对式(1)进行后向差分法离散化,整理后可得L1观测方程为

对式(2)进行后向差分法离散化,整理后可得L2观测方程为

对式(3)进行后向差分法离散化,整理后可得C 观测方程为

参数观测器结构如图5 所示。

图5 参数观测器结构Fig.5 Structure of parameter observer
在式(16)~式(18)中,等式右侧为当前时刻状态值或上一时刻状态值,均为已知量,故通过式(16)~式(18)可对L1、L2、C 实时观测估计,但上述观测结果在极点处即分母接近于0 时存在峰值,影响观测效果,故对极点处±π/6 的数值予以剔除,将其他时刻稳定的观测数据进行放大,以50 Hz 的频率进行平均化处理。
如图6 所示,观测器在一个工频周期0.02 s 后开始工作,0~0.06 s 工作值为L1=L2=2.5 mH、C=1.5 μF,0.04 s 后观测结果趋于稳定,观测结果为L1=L2=2.5±0.03 mH,C=1.5±0.05 μF;在0.06 s 后,工作值切换为L1=L2=5.0 mH、C=3 μF,0.09 s 后观测结果趋于稳定,观测结果为L1=L2=5.0±0.03 mH,C=3.0±0.05 μF。故分析可知,观测器精度未发生变化,机侧电感观测器误差和网侧电感观测器误差均在0.03 mH 以内;电容观测器误差在0.05 μF 以内。

图6 观测器效果Fig.6 Observation results
本文通过两步预测对延迟进行补偿,这就需要预测k+2 时刻的电容和电感,采用线性外推法进行预测,得到

故k+2 时刻的机侧电感L1(k+2)为

同理可得L2(k+2)和C(k+2)分别为

4 仿真分析
为验证所提出的控制策略,以两电平三相LCL型并网逆变器为控制对象,在Matlab/Simulink 中进行仿真验证,仿真参数如表2 所示。

表2 LCL 型并网逆变器仿真参数Tab.2 Simulation parameters of LCL-typegridconnected inverter
4.1 参数匹配的仿真
第1 组仿真为标称值和工作值一致的参数匹配仿真验证,如图7(a)所示,0~0.06 s 为第1 组参数L1=L2=2.5 mH、C=1.5 μF 的网侧电流波形,0.06~0.12 s 为第2 组参数值L1=L2=5.0 mH、C=3 μF 的网侧电流波形;由图7(b)可知第1 组参数值网侧电流的总谐波失真率THD(total harmonic distortion)为0.82%;在图7(c)中,第2 组参数值网侧电流的THD为0.37%。从图7 中可得到两点结论:首先,MPC 在参数匹配时控制效果比较好;其次,不同LCL 参数的滤波效果存在差异。

图7 参数一致时的并网电流波形及其THD 分布Fig.7 Waveforms of grid-connected current and distribution of THD with matched parameters
4.2 第1 组参数的参数失配及匹配仿真
第2 组仿真选取工作值为第1 组参数,如图8(a)所示,工作值为第1 组参数L1=L2=2.5 mH、C=1.5 μF,标称值为第2 组参数L1=L2=5.0 mH、C=3 μF,0~0.06 s 不采用观测器,0.06~0.12 s 采用观测器。从图8(b)和8(c)中可看出,采用参数观测器后,网侧电流i2的THD 从2.45%下降到了0.87%,THD 减少了1.58%,网侧电流质量得到明显改善。

图8 第1 组参数观测器效果对比Fig.8 Comparison results with and without parameter observer of Group-1
4.3 第2 组参数的参数失配及匹配仿真
第3 组仿真选取工作值为第2 组参数,如图9(a)所示,工作值为第2 组参数L1=L2=5.0 mH、C=3.0 μF,标称值为第1 组参数L1=L2=2.5 mH、C=1.5 μF。0~0.06 s 不采用观测器,0.06~0.12 s 采用观测器。从图9(b)和9(c)中可看出,采用参数观测器后,网侧电流i2的THD 从0.81%下降到了0.45%,网侧电流质量也有了一定的提升。

图9 第2 组参数值的观测器效果对比Fig.9 Comparison of results with and without parameter observer with Group-2
后面两组仿真验证了参数观测器的有效性,采用参数观测器后,两组网侧电流质量均有比较明显的改善,提高了功率因数,说明该策略可以有效地解决参数不匹配问题。
4.4 电网电压畸变情况下的仿真
电网在实际运行中,由于存在着非线性负荷,导致三相电网电压发生畸变,含高次背景谐波。所以,验证控制方法在电网电压发生畸变的情况下的运行特性是十分重要的。
如图10 所示,以a 相网侧电流和电网电压为例,在电网电压中注入幅值为10%的3 次和5 次谐波,网侧电流的THD 由未畸变时的0.45%变成了0.90%,说明该控制方法抑制电网电压畸变时的电流谐波能力较好,可以保证网侧电流在电网电压畸变时的电流质量。


图10 电网电压畸变情况下电流波形Fig.10 Waveforms of current under grid voltage distortion
4.5 考虑控制死区的仿真
为了保护逆变器的直流侧电源,需要在电力开关器件的控制信号中需加入死区时间,本文对3 个下管的控制信号延迟一个控制周期。
如图11 所示,以a 相网侧电流和电网电压为例,考虑控制死区后,网侧电流的THD 由未畸变时的0.45%变成了1.97%,说明该控制方法考虑控制死区时有着良好的电流调节能力,可以保证网侧电流在电网电压畸变时较好的电流质量。

图11 考虑控制死区情况下电流波形Fig.11 Waveforms of current considering the dead-time.
上述5 组仿真中,除第1 组外,其余4 组均是在含参数观测器的控制方法下进行的仿真实验,均验证了本控制方法的控制效果。
5 结语
本文采用一种多目标约束控制的MPC 控制方案,控制效果相比于传统MPC 控制方案有明显的改善。针对LCL 型并网逆变器标称值和工作值不匹配的问题,提出一种参数摄动MPC 方案,该策略实现简单,可降低MPC 对参数的依赖,有很好的控制效果。仿真实验表明:采用参数观测器的MPC 的三相LCL 型并网逆变器可以在电容和电感参数摄动的情况下保证网侧电流电能质量。
