一种新型大功率ZVZCS 三电平DC-DC 变换器
2022-04-19李启凡康家玉冯浪浪
李启凡,石 勇,康家玉,冯浪浪
(陕西科技大学电气与控制工程学院,西安 710021)
三电平DC-DC 变换器因其原边开关器件电压应力是Vin/2,且具有均压电路结构简单和软开关特性较好等特点,而被广泛应用于三相功率因数校正后级变换器和直流微电网等场合。IGBT 器件因其较强的通流能力成为大功率三电平DC-DC 变换器的首选器件[1-3]。实际应用中,三电平DC-DC 变换器中IGBT 器件的工作频率较高,其宽负载范围的软开关技术是必须解决的关键问题[5-12]。
三电平DC-DC 变换器的软开关技术可分为零电压开关ZVS(zero-voltage switching)[4-7]和零电压零电流开关ZVZCS(zero-voltage zero-current switching)[8-12]两种主流方案,其中ZVZCS 电路因可有效降低IGBT 拖尾电流损耗和原边换流损耗等优点,成为大功率高压直流变换场合的首选方案[3]。ZVZCS三电平直流变换器中,一部分原边开关利用副边电感储能与换流器件电容的能量实现ZVS 开通,另一部分原边开关因原边电流被复位至0 而实现ZCS 关断,与此同时原边换流损耗和占空比丢失问题都优于ZVS 电路[3-8]。目前主流的ZVZCS 电路有两种:副边钳位电路型[8]和原边钳位电路型[9]。副边钳位电路型ZVZCS 变换器在变压器副边增加有源开关或二极管及钳位电容组成钳位网络,在滞后桥臂换流时,钳位电容电压反射到变压器原边复位电流,该电路可有效减少占空比丢失现象[8-9]。研究表明,副边钳位电路型ZVZCS 变换器的主要问题是原边开关器件承受较高的电流过冲及钳位电容电流动态分布不均衡,上述因素导致该类电路不适用于大功率变换场合。原边钳位电路型ZVZCS 变换器在变压器原边串联隔直电容,续流时利用隔直电容电压复位原边电流,利用二极管或者饱和电感限制反向电流[9-10]。原边钳位电路型ZVZCS 变换器的主要问题是隔直电容电压纹波与整流二极管电压应力的折衷设计方法:一方面隔直电容电压大范围波动是快速复位电流的要求,另一方面电容电压大范围波动将严重影响系统效率并增加整流二极管的电压应力。因此,现有的原边钳位电路型ZVZCS变换器同样不适用于大功率变换场合。文献[13]指出随着变换功率的增加,ZVZCS 变换器存在如电流复位困难、原边器件电流过冲及整流二极管的电压应力增加等问题,如何克服这些困难是ZVZCS 三电平直流变换器亟待解决的关键问题。
针对上述问题,本文提出一种基于原边可变电压钳位电路的三电平DC-DC 变换器,其原边为4 个IGBT 串联,飞跨电容与双向开关串联将2 只超前管和2 只滞后管的开关过程连接起来,超前管和滞后管的中点依次接隔直电容和变压器,飞跨电容串联双向开关可防止电流复位后反向;副边采用全波整流和LC 滤波结构;钳位电路输入为母线电压,经由二极管组成的超前管与MOSFET 组成的滞后管形成的三电平电路后经变压器输出,钳位电路复位变压器的输出与主功率变压器原边串联,在正常工作时复位变压器原、副边电压为0,在电流复位阶段变压器两端短时承受一定电压应力,变压器伏秒积很低,因此复位变压器体积远小于主功率变压器。该变换器具有主开关器件软开关负载范围宽、钳位电路变压器体积小、原边电流复位快、飞跨电容的电流应力小、开关管电流分布均衡、副边整流二极管电压小和占空比丢失少等优点,且钳位电路开关管和双向开关均可在全负载范围内实现软开关。本文分析了变换器的组成及工作原理和电路的基本特性,设计了6.5 kW 的实验样机,理论与实验结果表明该电路工作原理正确,可正常工作。
1 电路拓扑结构
图1 是新型大功率ZVZCS 三电平DC-DC 变换器的电路拓扑。原边电路中:Vin为直流输入电压;VT1、VT2、VT3和VT4为原边主开关器件;D1、D2、D3和D4为IGBT 反并联二极管;C1和C4为IGBT 输出结电容;Css为飞跨电容,与输入母线电压共同钳位原边开关器件电压应力;开关管Qa1和Qa2构成的双向开关与Css串联,防止原边电流复位后反向;Cbl为隔直电容,在电路的负半开关周期为负载提供能量;Lp为变压器漏感。副边电路中:Do1和Do2为副边全波整流二极管;Lo和Co为输出滤波电路;Ro为负载。原边电压可变钳位电路输入为直流母线电压,Cin1和Cin2为分压电容,采用二极管Dr3、Qr1、Dr4和Qr2所组成的开关网络控制变压器T2原边电压,功率传输时是压vr1=0,电流复位时vr1=±Vin/2。k1为变压器T1变比,k2为T2变比,Ts为周期,D 为占空比。

图1 新型大功率ZVZCS 三电平DC-DC 变换器Fig.1 Novel high-power ZVZCS three-level DC-DC converter
2 工作原理分析
图2 为本文所提变换器的典型波形,其中:VT1、VT2、VT3、VT4、Qr1、Qr2、Qa1和Qa2为开关 器件的驱动信号;vp为变压器原边电压;ip为原边电流;vr2为复位电路输出电压;iDo1和iDo2为整流二极管电流。

图2 典型波形Fig.2 Typical waveforms
该电路拓扑半个周期模态如图3 所示。讨论前,假设所有功率器件为理想器件,忽略驱动电压上升时间;隔直电容较大,近似认为其两端电压不变;滤波电感较大,可忽略电流纹波。

图3 半个开关周期的模态Fig.3 Modes over one half of switching cycle
模态1[t0之前]:VT1和VT2开通,输入电压通过变压器T1给负载供电,变压器副边Do1导通,原边电流ip给隔直电容Cbl充电,由于Cbl很大,因此稳定状态时=Vin/2,则ip为

变压器两端电压vp为

复位电路Qr1和Qr2开通,电流ir=ip/k2,复位电路变压器副边电压vr2=0,双向开关Qa1和Qa2开通,飞跨电容上无电流通过。
模态2[t0~t2]:在t0时刻,VT1关断,ip给C1充电,同时C4通过Css放电,变压器原边电压线性下降。由于C1和C4减缓了上升速度,降低关断损耗,VT1为ZVS 关断,漏感Lp和滤波电感Lo串联,储能反射到变压器原边用于电容充放电,ip近似不变,类似于一个恒流源,其大小为

同时,ip给Cbl充电,C1电压线性上升,C4电压线性下降,即
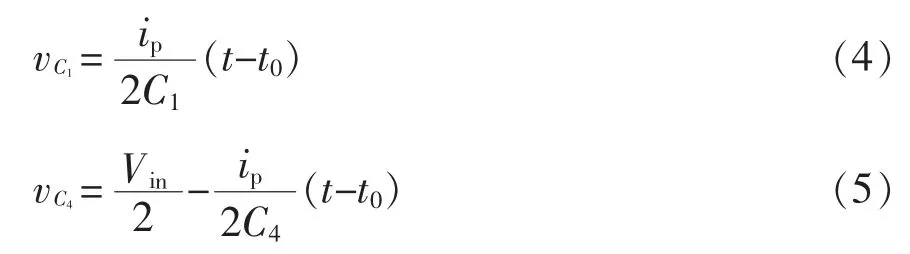
在t1时刻,C1的电压上升到Vin/2,C4的电压下降到0,D4自然导通。该模态的持续时间为

由于D4导通,原边电流缓慢减小,不足以提供负载所需电流,副边整流二极管Do1和Do2同时导通。
模态3[t2~t3]:在t2时刻,由于D4已经导通,C4电压被钳位在0,因此VT4为ZVS 开通,VT1与VT4的死区时间大于Δt0-1,保证VT4可ZVS 开通。同时Qa1和Qr2为ZVS 关断,复位电路变压器输出电压为

此时,变压器漏感Lp两端电压为-vr2,电流ip线性减小,即

在此阶段,ip流经飞跨电容和双向开关,由于ip受到反向电压的作用,开始快速减小,变压器副边Do1和Do2仍同时导通,变压器副边电压为0。这个模态结束电流复位至0,可得出电流ip复位至0 的时间为

模态4[t3~t4]:t3时刻,ip降为0,由于Qa1已经关断,因此ip复位至0 后不会反向增加。同时,复位电路输出电压vr2=0,变压器原、副边电压均为0。变压器副边Do1和Do2同时导通,均分负载电流。
模态5[t4~t6]:在t4时刻,由于ip已经复位至0,因此VT2为ZCS 关断,同时Qa1和Qr2为ZCS 开通。短暂的延时后,在t5时刻,开通VT3,由于变压器漏感作用,ip不能突变,VT3为ZCS 开通,储存在Cbl中的能量为负载供电,副边2 个二极管仍然同时导通,变压器原、副边电压被钳位在0。此时漏感两端电压为,ip开始反方向线性增加,即

变压器副边Do1上的电流开始减小,Do2上的电流开始增大。当ip反方向增加到Io/k1时,此模态结束,该模态持续时间为

此时复位电路电流ir=-ip/k2,复位电路变压器副边电压vr2=0,飞跨电容上无电流通过。
模态6[t6~t7]:从t6时刻开始,原边为负载提供能量,同时给隔直电容反向充电。Do1关断,所有的负载电流均流过Do2,在t7时刻,关断VT3,开始负半周期,工作情况类似[t0~t6]。
3 电路特性分析
3.1 VT2 和VT4 的软开关
开通时刻:VT2和VT4可实现零电压开通,由于变压器漏感和滤波电感的存在,其所储存的能量足够提供C2和C4充、放电过程所需要的能量,因此可在宽负载范围内实现ZVS 开通,即有

关断时刻:以VT2为例分析。t2时刻起,VT4开通,Qr2关断,变压器原边电压已降至0,Qa1关断,保证电流在复位至0 后不会反向增大,变压器漏感Lp两端电压为-vr2,即

电流复位时间为

Treset的长短与最大有效占空比Deff、IGBT 拖尾电流的复位时间Tzcs和变压器漏感造成的占空比丢失Dloss有关,可表示为
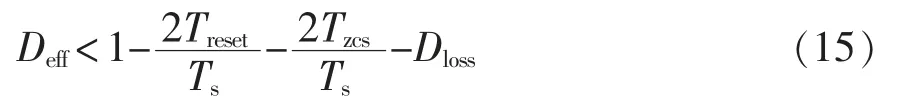
其中,Tzcs由IGBT 特性决定。由图2 可知,Δt5-6为漏感造成的占空比丢失,由式(11)可得

则Deff与占空比D 之间满足

将式(16)和式(17)代入式(15)可得Treset应满足

将式(18)代入式(14)可得复位电压vr2满足

3.2 VT1 和VT3 的软开关
开通时刻:VT1和VT3开通时,由于Lp的存在,限制ip的变化率,使得ip从0 缓慢增长,因此VT1和VT3为ZCS 开通,实现了开通损耗最小。由于开通损耗取决于ip的增加速率和的降低速率,故VT1和VT3的驱动电路中,较小的驱动电阻和较大的漏感有利于降低该损耗,但是较大的Lp会延长原边电流的复位时间,增加VT2和VT4零电流关断的难度,因此变压器漏感应是原边器件的ZVZCS和ZCZVS 软开关状态的折衷设计。
关断时刻:当VT1和VT3关断时,由于结电容的存在,不会突变,因此VT1和VT3为ZVS关断,C1和C3较大可降低关断损耗,与此同时也不会增加VT2和VT3的零电流开通难度。
3.3 Qa1 和Qa2 的软开关
开通时刻:Qa1和Qa2开通时变压器T1原边电流已经复位至0,飞跨电容上无电流通过,因此Qa1和Qa2为ZCS 开通。
关断时刻:由于Qa1和Qa2关断时体二极管导通,Qa1和Qa2为ZVS 关断。
3.4 Qr1 和Qr2 的软开关
开通时刻:Qr1和Qr2开通前变压器T1原边电流已经复位至0,复位电路中无电流通过,因此Qr1和Qr2为ZCS 开通。
关断时刻:由于Qr1和Qr2的结电容因素,开关管两端电压不能突变,Qr1和Qr2为准ZVS 关断。
3.5 复位电路复位电压的设计
复位电路在电路续流阶段给漏感施加反向电压,实现原边电流的快速复位。由式(14)可得复位电压为

由式(20)可知,复位电压与主回路变压器漏感、原边电流及复位时间有关。因此可得在复位时间一定的条件下,复位电压与主回路变压器漏感和原边电流的关系如图4 所示。在变压器漏感一定的条件下,复位电压、复位时间和原边电流的关系如图5 所示。
由图4 可知,当复位时间一定时,若输出电流和变压器漏感较大,则所需的复位电压越大。由图5可知,当变压器漏感一定时,若要保证复位时间更快,则复位电压需更大。在实际工作环境中,综合上述分析,当输出功率、变压器漏感及复位时间三者都满足条件时,根据变换器滞后管的软开关负载范围可确定复位电压。
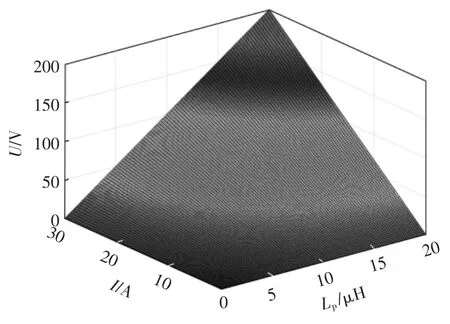
图4 复位电压与电流和漏感变化Fig.4 Changes in voltage of reset with current and leakage inductance
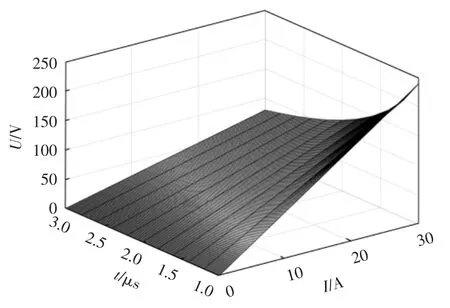
图5 复位电压与电流和复位时间变化Fig.5 Changes in voltage of reset with current and time of reset
根据电路工作原理,可得输出电压与输入电压的关系为
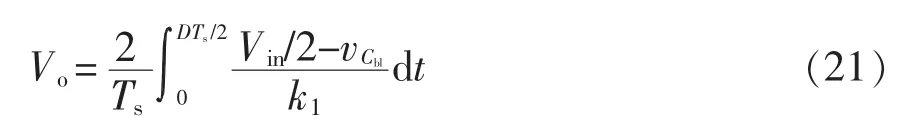

由式(16)可得丢失占空比为
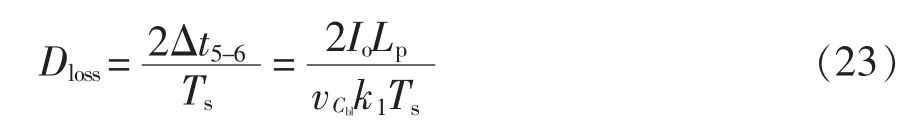
实际输出电压为

根据输入、输出电压设计可得主变压器变比k1为

式中,Dmax为最大占空比,Dmax=0.7。
本样机设计输入电压为560 V,输出电压为24 V,输出电流为280 A,复位时间为1.5 μs,变压器漏感为8 μH,由式(13)可知复位电路变压器变比为

其中

将式(27)代入式(26)可得


主回路变压器原边电流ip为

将k1=8 代入式(30)可得

将k2=1.5 代入式(26)可得

由式(9)可得复位电压为186.7 V 时所需的复位时间为

根据驱动时序设计,预留电流最大复位时间为3 μs,因此本文实验样机可在规定的时间内完成电流复位,原边电流满足复位条件。
3.6 复位电路变压器体积
变压器T2的原、副边只在电流复位阶段承受电压,根据伏秒积公式可计算变压器磁芯横截面积,即

式中:V 为变压器工作时的电压,V;Ton为变压器T2原、副边电压不为0 的时间,s;B 为磁芯磁感应强度,Gs;N1为变压器初级线圈最少匝数;K 为常数,用来统一单位;S2为变压器磁芯的横截面积,cm2,表示为

代入参数可得主回路变压器T1和复位电路变压器T2磁芯横截面积与工作时间之间的关系,如图6 所示。
由图6 可得,当变压器工作时间Ton相同时,主回路变压器T1磁芯横截面积大于复位电路变压器T2的横截面积。根据本文电路的工作原理可知,主电路变压器的Ton远大于复位电路变压器的Ton,因此主变压器磁芯横截面积必然远大于复位电路。通过具体计算验证2 个变压器磁芯横截面积的关系。

图6 磁芯横截面积与时间的关系Fig.6 Relationship between core cross-sectional area and time
在输入电压一定的条件下,计算复位电路变压器T2磁芯横截面积,其中V=280 V,N1=5,由式(33)可知复位时间Ton=1.44 μs,常数K=1。取磁感应强度为0.2 T,可得变压器T2磁芯横截面积为
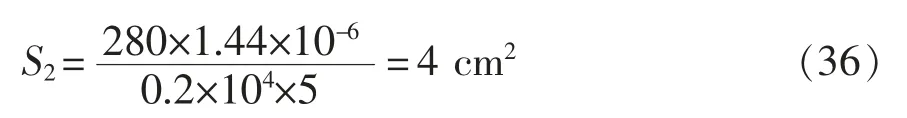
计算主电路变压器T1磁芯横截面积,其中V=280 V,Ton=20 μs,N1=8,常数K=1,取磁感应强度为0.2 T,可得变压器T1磁芯横截面积为

由式(36)和式(37)可知,S1约为S2的8.7 倍,因此复位电路变压器体积远小于主回路变压器。
3.7 对比分析
为进一步说明本文电路的优缺点,选取文献[13]的电路进行比较研究。本文电路最大的优点在于原边电流的复位电压不增加主功率器的电压和电流应力,且复位作用的强弱可依据需要通过复位变压器变比调节。文献[13]电路仍采用隔直电容提供原边电流复位电压,一方面复位电压增加整流二极管的电压应力,另一方面复位电压的幅值可设计自由度较小,使该电路难以应用到大功率场合。
1)整流二极管的应力比较
本文电路的整流二极管电压应力小于文献[13]电路的。文献[13]电路的整流二极管电压应力为

式中:Vin为输入电压;kt为变压器变比;为隔直电容最大电压。整流二极管上的附加电压应力为vRD_ADD,由允许的最大负载电流所决定,表示为

式中,Treset为最大复位时间。将式(40)代入式(39)可得

文献[13]中kt=8,Treset=6 μs,可得vRD_ADD与变压器漏感Lp和负载Iomax电流之间的关系如图7 所示。
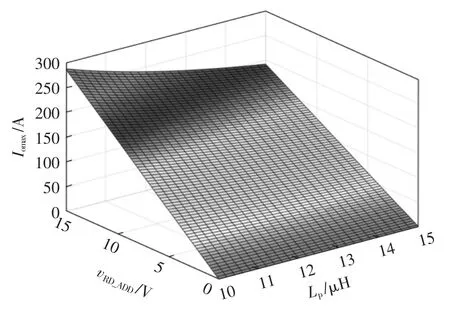
图7 Iomax 与Lp、vRD_ADD 的关系Fig.7 Relationship among Iomax,Lp,and vRD_ADD
由图7 可知,当变压器漏感一定时,负载电流越大,整流二极管所承受的附加电压越大,整流二极管电压应力会随着负载电流的增加而增加。
本文所提电路拓扑整流二极管的电压应力为

由图7 和式(41)可得,随着负载电流Iomax的增加,文献[13]整流二极管的电压应力明显增加。
图8 为仿真验证结果,在输出电流280 A 条件下,文献[13]整流二极管电压应力比本文电路高45 V;在输出电流550 A 条件下,文献[13]整流二极管电压应力比本文电路的高90 V。综上所述,本文电路具有副边整流二极管电压应力小的特点。

图8 整流二极管电压应力仿真对比Fig.8 Simulation comparison of voltage stress of rectifier diode
2)复位电路通态损耗比较
文献[13]中MOSFET 串联双向开关Sa3和Sa4(与本文Qa1和Qa2相同)只在电流复位阶段参与电路工作,在正常工作阶段Sa3和Sa4上没有电流通过,因此通态损耗较小。本文电路中Qr1和Qr2在功率传输阶段存在环流ir,因此通态损耗较大。
4 仿真与实验结果分析
实验装置使用的主要开关器件型号和设计参数分别如表1 和表2 所示。
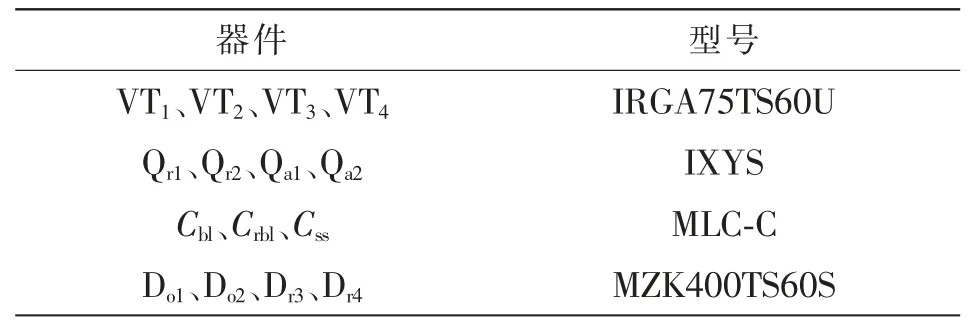
表1 器件型号Tab.1 Types of devices
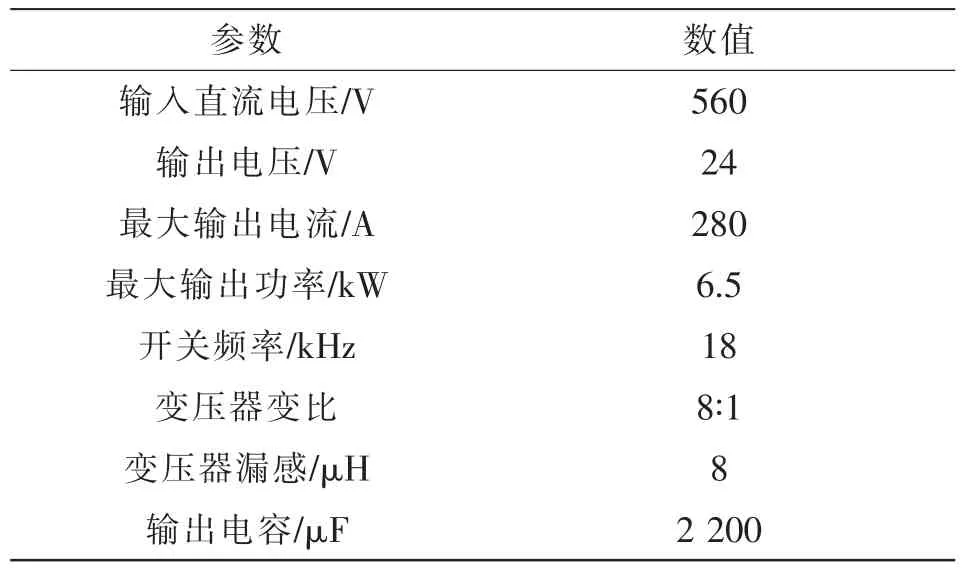
表2 设计参数Tab.2 Design parameters
图9 为实验波形。图9(a)为变压器原边电压和原边电流波形,功率传输阶段,变压器原边电压约±280 V,原边电流约±33 A,原边电流的变化率由输出滤波电感决定,变压器漏感在续流初始阶段承受反向电压,导致原边电流迅速复位,复位电压的大小与复位电路变压器T2的匝比有关;图9(b)为整流二极管电压和电流波形,此时整流二极管承受电压为70 V,整流二极管电压应力不因复位电路的加入而增大;图9(c)为VT4的栅极和发射极之间的电压、集电极和发射极之间的电压与电流,可以看出,VT4可实现零电压开通,零电流关断,图中VT4电压上升时刻出现的电流为结电容和吸收电路的充电电流;图9(d)为VT3的栅极和发射极之间的电压,集电极和发射极之间的电压与电流,可以看出,VT3可实现等效零电流开通,等效零电压关断;图9(e)为复位电路Qr2的栅源极间的电压、漏源极间的电压与电流,可以看出,Qr2可实现零电压关断,零电流开通。图9(f)为复位电路变压器原边电压和电流,在电流复位阶段,复位电路产生反向电压使得电流快速复位,与图9(b)结合可知,复位电压不会增加整流二极管电压应力。图9(g)为隔直电容两端电压,隔直电容在一个工作周期内充、放电维持电荷平衡,其电压稳定在280 V。图9(h)为飞跨电容两端电压,在一个周期内,其平均电压可稳定在280 V。
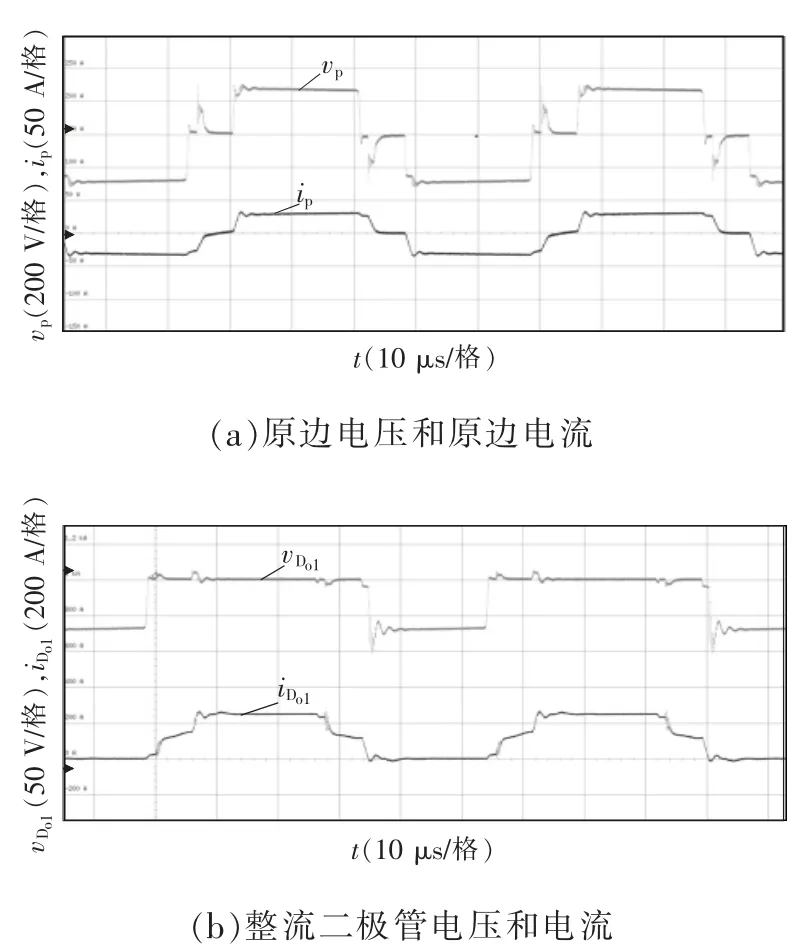
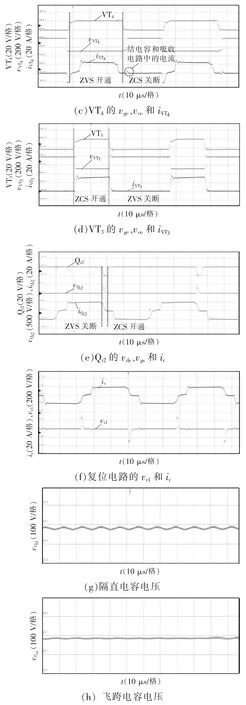
图9 实验波形Fig.9 Experimental waveforms
图10 为电路的PSIM 仿真波形。对比图9 与图10 可知,实验与仿真结果基本符合。


图10 仿真波形Fig.10 Simulation waveforms
图11 给出在负载电阻为0.085 Ω 的条件下,效率曲线随输入电压变化的趋势,实验装置最高效率为95.6%。

图11 效率曲线Fig.11 Efficiency curve
5 结论
本文提出一种新型大功率ZVZCS 三电平DCDC 变换器,在变压器原边电路增加复位电压可变钳位电路实现原边电流有效复位,该电路克服现有ZVZCS 变换器的问题,具有主开关器件软开关负载范围宽、复位电压不影响主功率器件的电压和电流应力等特点,因此适用于大功率应用场合。通过分析和实验可得以下结论:
(1)复位电压可变钳位电路工作原理正确,原边开关器件在宽负载范围内实现软开关,所有辅助开关全负载范围实现软开关。
(2)钳位电路的变压器原、副边只在电流复位阶段承受电压,因此其体积远小于主回路变压器。
(3)负载电流增大时,整流二极管的电压应力不受复位电压影响。
