微纳操纵成像迭代学习前馈反馈控制研究

吴文鹏，王一帆，胡贞

（长春理工大学 电子信息工程学院，长春 130022）

随着科技的快速发展，科研界以及整个社会逐渐将视野从传统的宏观世界转向到微观世界，而微纳操纵成像系统作为沟通宏观与微观世界的的桥梁，其重要性越发突出，不仅在材料检测行业有着举足轻重的地位，还与生命学科紧紧联系，包括生物细胞的样貌成像与细胞电、力学特性研究。目前，商用的系统大都采用比例积分微分（Proportional integral differential，PID）控制，而传统的PID控制方法存在跟踪精度差、参数难调节等缺点，影响着系统最终成像质量。因此，寻找合适的控制算法来提高系统的跟踪精度很有必要。

目前提高成像精度的方法，从算法软件着手主要包含两方面：1）根据PID参数难调节的缺点，将智能控制方法与PID参数调节相结合，如王一帆等人，用模糊控制方法对PID参数进行实时调节，仿真结果显示，基于模糊方法的控制系统具有较好的动态性能[1]；南开大学的周娴玮提出将继电反馈的PI控制参数整定方法运用到原子力显微镜系统中，用于解决系统比例积分（Proportional integral，PI）参数难整定的问题[2]。Liu等[3]将具有严格数学描述的迭代学习用于参数整定，并进行了实验验证，在该算法下的成像图片更加清晰，样品分层处明显。2）根据PID控制器跟踪精度低，鲁棒性差的问题，专家学者考虑直接用智能、鲁棒控制器替换PID控制器，如Xie等[4]将模型预测控制与闭环迭代学习结合，形成基于模型信息的预测学习控制方法，有效的提高了成像质量与成像速度。电子科技大学的李丹等将迭代学习应用于系统横向扫描定位[5]，显著提高了成像质量。如Chen等[6]将自抗扰控制方法引入系统中，提高了系统的鲁棒性。

由于PID控制存在固有问题，即使进行参数调优，结果也是差强人意。而更换一般的智能控制方法，却忽略了系统的重复工作特性和被测样品的周期性。学习控制顾名思义具有学习功能的控制方法，根据系统实际运行轨迹与期望轨迹之间的误差，利用学习的经验来产生一个新的输入，使系统更好的逼近期望的输出。迭代学习作为最初的学习控制方法，适用于具有重复运行性质的系统[7]，而传统的开环型迭代学习与闭环型迭代学习都存在一定的缺点，所以本文采用具有开闭环学习律的前馈—反馈控制，并根据框图，给出系统收敛证明。同时改变传统的固定学习增益，运用指数变增益作为新的学习律[8]，能在加快收敛速度的同时得到最小的收敛误差。

1 微纳操纵成像系统

1.1 系统结构与扫描方式

微纳操纵成像系统的结构图如图1所示，当激光器发射激光照射在微悬臂，由于光偏转原理，被反射至四象限光斑探测器上，探测器采集到电压值信号被A/D采集卡传输到计算机内，进行算法数据处理，计算机再将处理完的数据发送到扫描器，进行成像扫描，由于样品与探针之间范德华力的因素[9]，微悬臂产生偏转，导致光斑在四象限探测器的位置发生位移，计算机利用这个偏转量行成像。

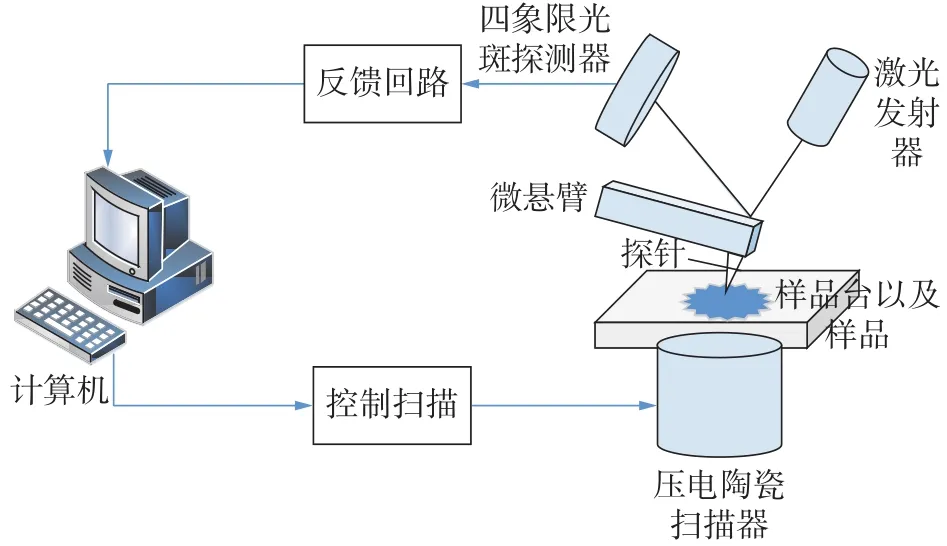
图1 微纳操纵成像系统结构图

系统在进行成像时，采用样品光栅式扫描，所以系统具备重复运行的性质，如图2所示。实验室自制微纳操纵成像系统扫描时， 保持探针不动，扫描器托着样品台进行移动，图中，先是沿着X轴扫描第一行，随后返回扫描初始点，接着向Y轴移动一个步长，再进行X轴第二行扫描，同时在纵向Z轴上，探针随着样品形貌起伏进行运动成像。由于横向X、Y轴只进行平行移动，所以主要靠纵向反馈量进行控制成像，包括下文所建立的模型和控制方法均是建立在纵向基础上。

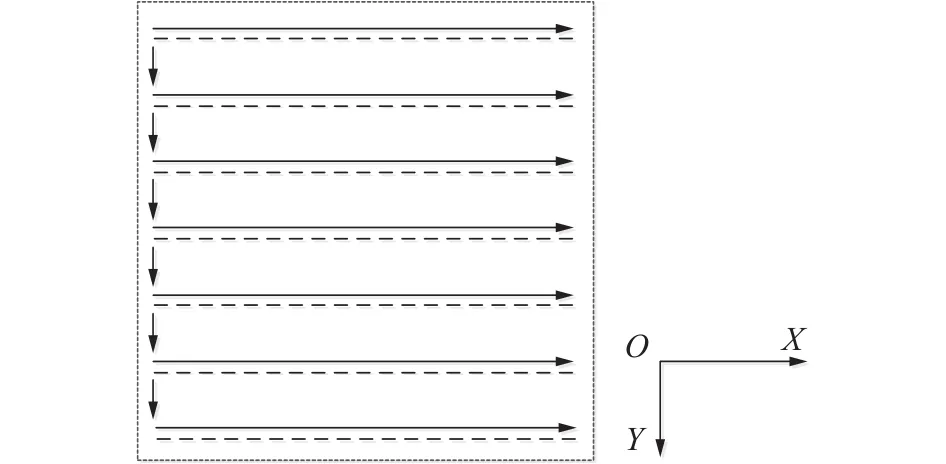
图2 微纳操纵成像系统扫描方式

1.2 系统数学模型

由图1所示，系统整体由多模块组成，难以直接对系统建立数学模型，可以对各模块分别建立，最后组成系统整体的数学模型。同时可以根据各模块的工作性质，分别采用机理建模方法与实验数据建模方法。如图3为微纳操纵成像系统的模型框图。

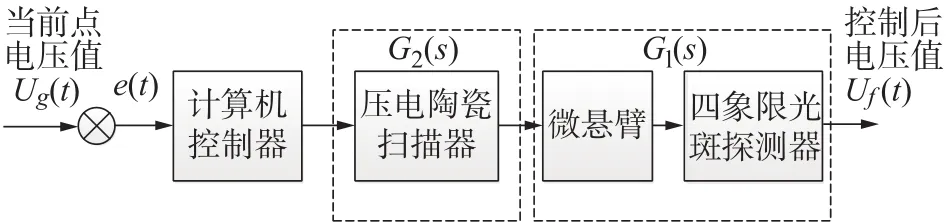
图3 系统数学模型框图

1.2.1 微悬臂

微悬臂部分采用机理建模的方法，根据微悬臂在工作时的特性，采用光偏转原理进行建模，如图4所示。

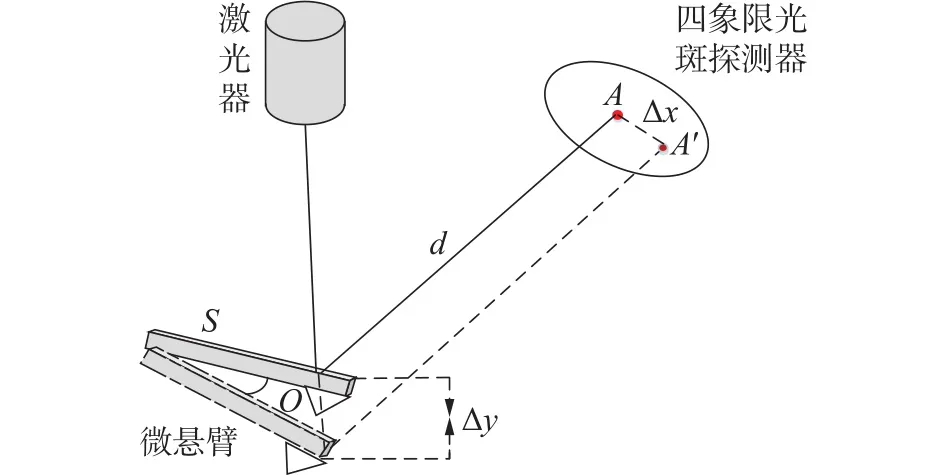
图4 光偏转原理图

激光经过光反射至四象限光斑探测器中心A点，扫描时，因为原子力等因素，微悬臂产生位移形变。偏转量记为Δy，偏转角度为O，同时光斑点移至到A′点，光斑偏转角度为2O，对应光斑探测器上的位移量记为Δx。设探针微悬臂长度为s，反射长度为d，可用近似公式表示为[10]

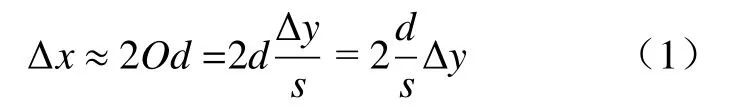
其中：实验室自制微纳操纵成像系统，所用的探针微悬臂长度s=450 μm；微悬臂与四象限光斑传感器距离d=11.5 cm，则可得出放大倍数约为511。

1.2.2 四象限光斑探测器

四象限光斑探测器模块，采用实验数据建模，通过手调移动四象限光斑探测器。由于四象限光斑探测器的对称性，只需要进行水平轴方向移动即可。首先移动平台向右，即光斑位置相对平移向左，接着反方向重复相同动作，每次移动0.05 mm，记录每次位移的电压值，选择有效数据，利用四象限光斑探测器采集的电压值随光斑位移量变化关系进行建模。用MATLAB拟合工具进行数据拟合，如图5所示。

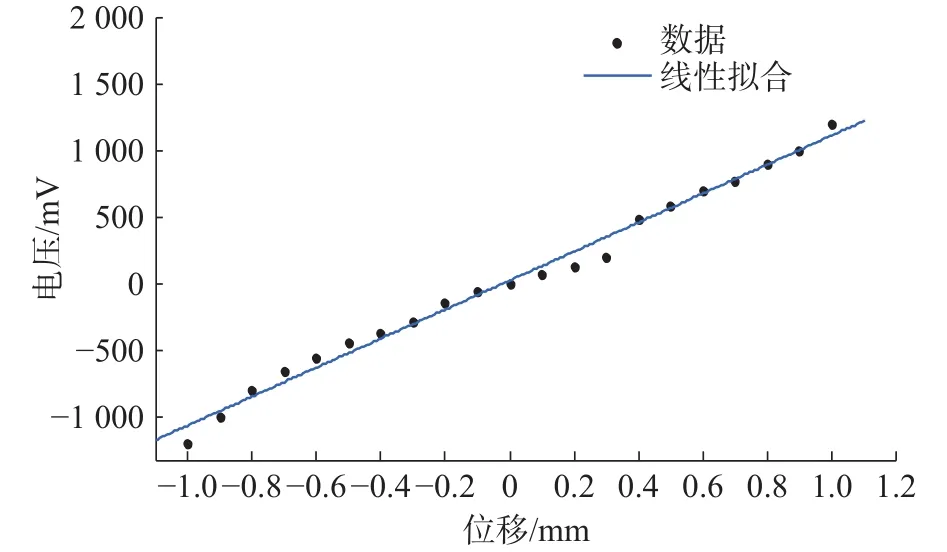
图5 光斑探测器函数拟合图

得到1阶比例传递函数，模型公式为

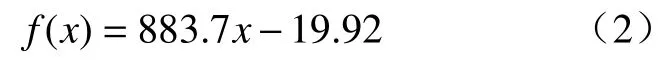
至此，静态部分的传递函数可看成两个比例放大倍数的乘积，微悬臂放大倍数为511，而光斑探测器每移动1 μm，变化值为0.883，表达式为

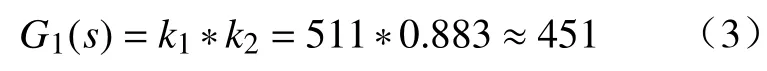
1.2.3 压电陶瓷扫描器

压电陶瓷的工作原理是逆压电效应，由于其自身的迟滞非线性，实验室自制系统中，已经采用了PI控制器对压电陶瓷进行了补偿控制，其闭环控制结构图如图6所示。

图6 压电陶瓷闭环控制结构图

为了方便后续建模、控制器设计以及仿真分析，对压电陶瓷进行建模时，可以通过PI公司自带的黑匣子软件对其输入0.1 mV阶跃信号，输出波形如图7所示。

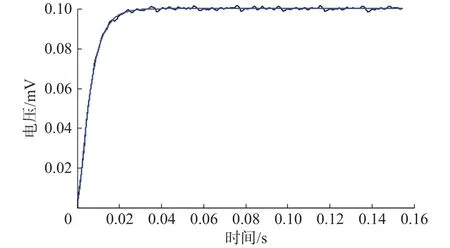
图7 压电陶瓷响应曲线

利用平滑滤波法滤除噪声信号，根据输出波形进行函数拟合，拟合函数为

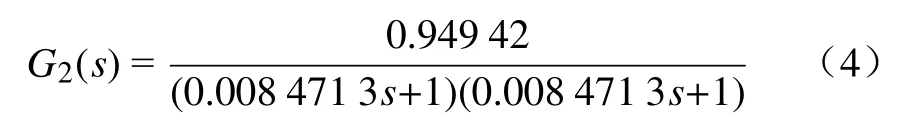
所以微纳操纵成像系统的整体数学模型为

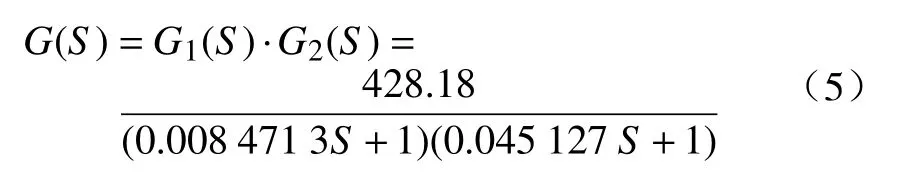
2 迭代学习控制算法

迭代学习作为最初的学习控制，是智能控制的研究热点。它适用于具有重复性质的被控对象，能够在有限区间[0T]上实现完全跟踪，这里的完全跟踪是指系统运行的整个过程，无论是暂态还是稳态情况下保持跟踪目标轨迹，即实现系统实际输出与期望输出的误差为0，同时要求收敛速度要快[11]。

根据迭代学习的学习律性质，可以分为开环、闭环、开闭环迭代学习。开环迭代学习由于控制本质是开环控制，不能保证系统的稳定性，且最终的收敛误差不尽人意，同时它只利用了前一次的误差信息。而闭环迭代学习只利用当前运行信息，没有考虑上一次迭代运行状态信息，且为了减小收敛误差，需要较大的反馈增益，容易引起系统振荡。所以本文采用开闭环学习律，可以综合利用两者之间的优点。

2.1 迭代学习前馈反馈控制

2.1.1 控制器结构

反馈-前馈迭代学习控制器结构如图8所示，它是由前馈控制器和反馈控制器并联组成[12]，两者还可以分别作用于系统，且反馈控制器对前馈控制器的收敛性影响不大。

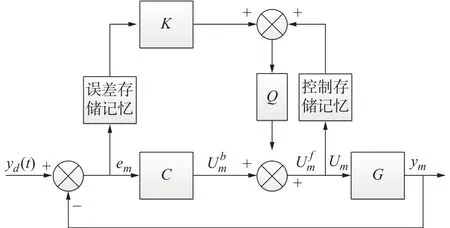
图8 反馈−前馈迭代学习算法结构图

图8中K为前馈控制器，采用开环迭代学习律，C为反馈控制器，由于迭代学习控制本身具有积分效应[13]，所以实际系统中不需要再加入积分环节，本文采用闭环指数变增益PD型控制器算子，Q为滤波器，G为被控对象，yd为期望输出值，ym为实际输出值，em为跟踪误差，Um为控制信号，通过存储单元不断迭代更新控制信号输入到被控对象。

2.1.2 收敛性分析

迭代学习收敛性分析是确保控制器能否正常工作的前提，一般有两种方法进行证明，包括时域和频域的分析。考虑系统结构，我们采用频域分析法[14]。

通过压缩映射原理，系统在被控对象G、开环学习K以及闭环反馈学习C的作用下，如果满足：

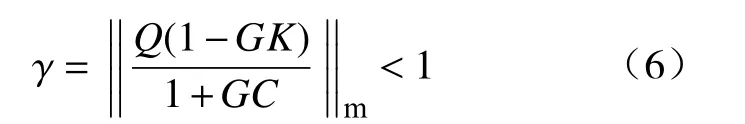
则当m→∞时，em+1将会收敛于一个平衡点。

证明如下：

用迭代学习控制前馈输出量为

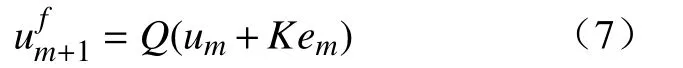
反馈控制量为

从图8可以看出：

由式（7）、式（9）可得控制律为

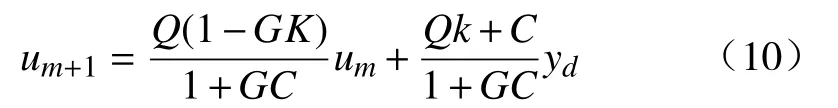
跟踪误差为

如果对于任意m，em+1满足下列不等式：

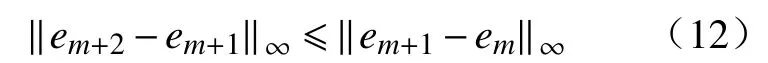
那么em+1将会收敛于一个平衡点。

由式（11）可得：

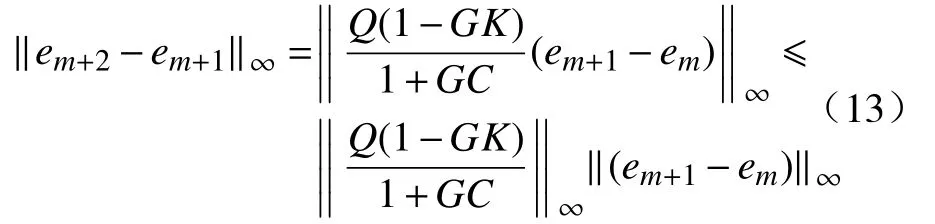
如果要对每一次迭代总是成立，就必须满足下列条件

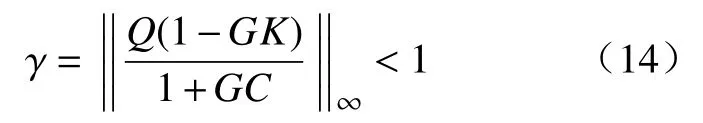
证毕

2.2 算法实现

从证明可以看出，设计前馈—反馈迭代学习控制器，主要设计反馈控制C、前馈控制K以及滤波器Q。

2.2.1 反馈控制器

选用开环迭代学习控制，前提是假设系统稳定，但实际对于模型信息不确定、不稳定且有非重复性扰动的系统，开环迭代学习就显得力不从心，所以反馈控制器作用十分重要，目的是为了保证跟踪误差一致有界性，使系统快速稳定，这样迭代学习才能收敛，采用闭环PD型指数变增益的迭代学习作为反馈控制器，传统学习律都是固定增益的，导致系统并不能更好的跟踪期望轨迹，所以采用指数变增益。具体控制律为

2.2.2 前馈控制器

由式（14）可知，当反馈控制C=0时，那么该式就化为 ‖Q(1−GK)‖∞< 1。从理论上的来说，前馈控制器最佳选择是K=G−1。但是在实际系统中，由于系统的复杂性和非线性，不能精确地辨识出系统的传递函数，那么就很难确定前馈控制器，但是迭代学习算法并不十分依赖模型的具体信息，降低了对前馈控制器的要求，可以根据系统的初步辨识，进行设计。

2.2.3 滤波器

由于干扰、以及系统模型不确定性等因素的影响，控制信号中可能会含有高频噪声信号等[15]。但需要的信号常常在低频率段，常规的开闭环学习律控制会容易分散，为了衰减高频段，选择低通滤波器，理论上最佳选择为Butterworth低通滤波器，则

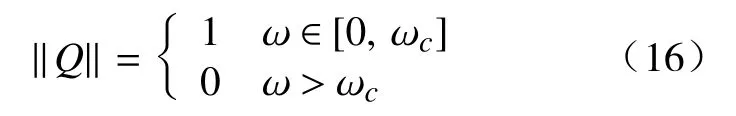
式中：ω为频率； ωc为截止频率。

3 仿真试验

根据所建立的模型进行仿真试验，经过多次试验调试，控制器具体数值如下：

反馈控制器为

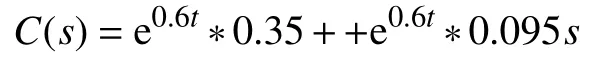
前馈控制器为

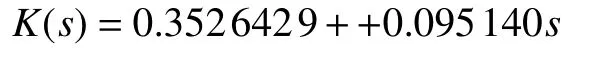
滤波器Q（s） = 1/s+ 100；

收敛性验证，将所设计的控制器，代入式（14）中，通过函数的bode图进行验证。

将bode图的幅频换成幅值的绝对值，如图9所示。可以清楚的看到，最大值为0.014 mg，且值小于1。说明所设计的控制器是收敛稳定的，且值越小收敛速度越快。

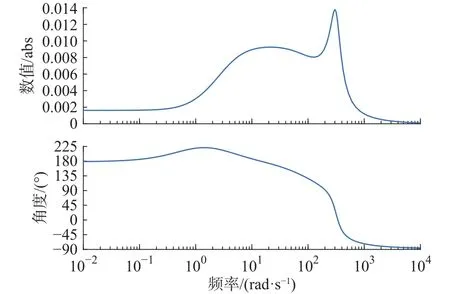
图9 收敛证明 bode 图

在MATLAB/simulink中搭建仿真模型图，编写s函数程序，运行主程序main，进行仿真实验，仿真结构图如图10所示。

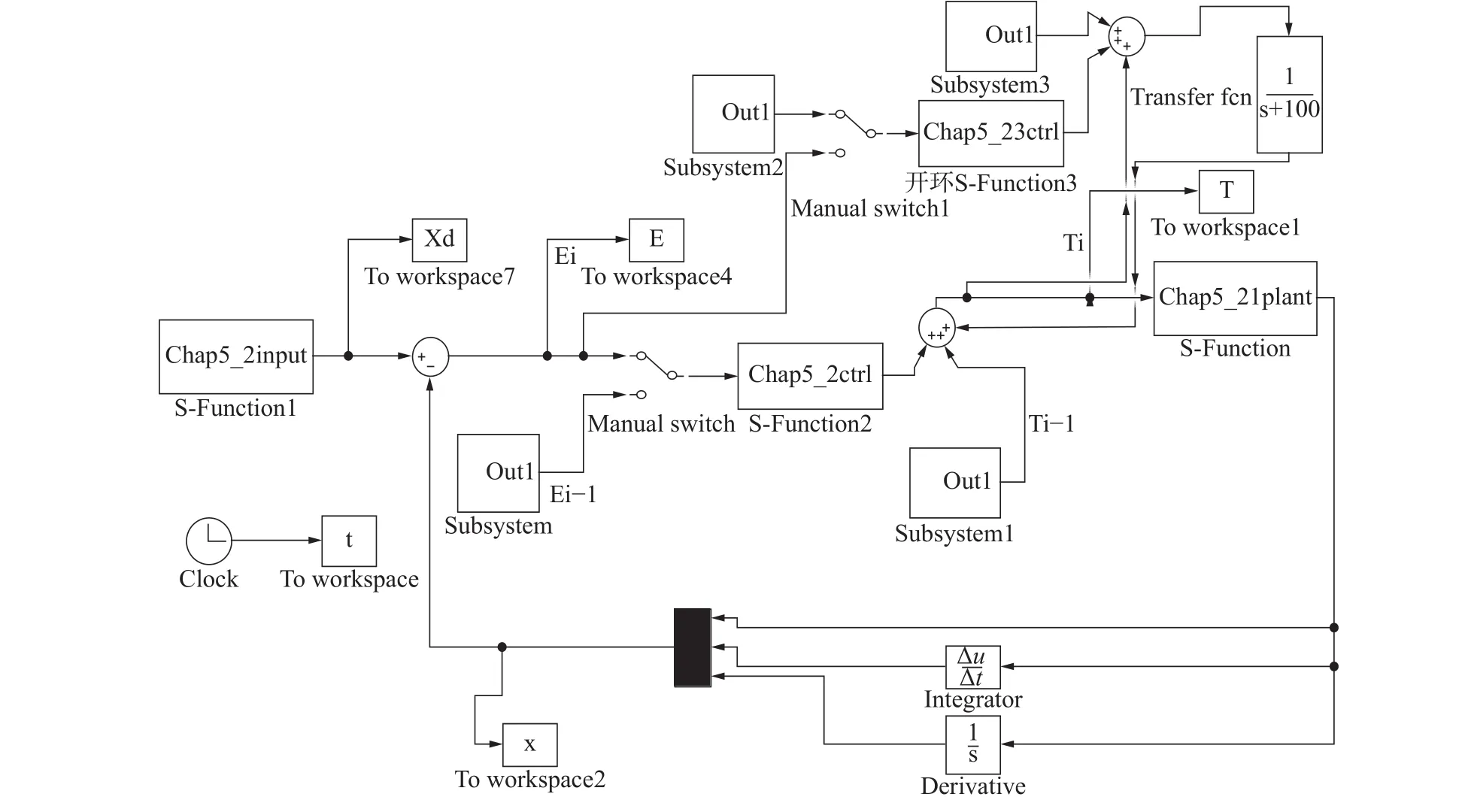
图10 仿真结构图

设计学习控制器，主要是提高系统的跟踪精度，考虑实际系统被测样品形貌呈周期性排列，如光栅、生物细胞等[16]，给定预期轨迹为

分别进行PID控制，与各学习律控制仿真，采样时间为 0.001 s，仿真时间为 2 s，迭代次数为 10 次，结果如图11所示。

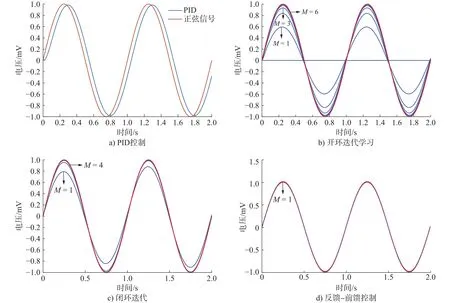
图11 正弦波跟踪曲线

进行误差对比分析，具体结果如图12与表1所示。

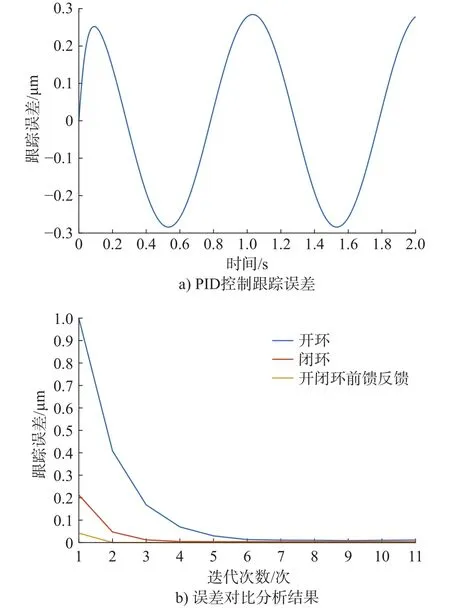
图12 误差对比分析结果

表1 正弦波仿真结果对比表

目前系统采用的传统PID控制方法，误差稳定在 0.3 μm，前馈反馈控制最大误差为 0.2 nm，可见所设计的控制器控制精度最高，完全符合扫描纳米精度要求。

为了更好的模拟光栅扫描过程中的跟踪情况，给定期望轨迹为2πt，占空比为50%的方波信号，如图13所示，相较于PID控制，第10次迭代学习前馈反馈控制，使系统能更快更平缓的响应曲线。

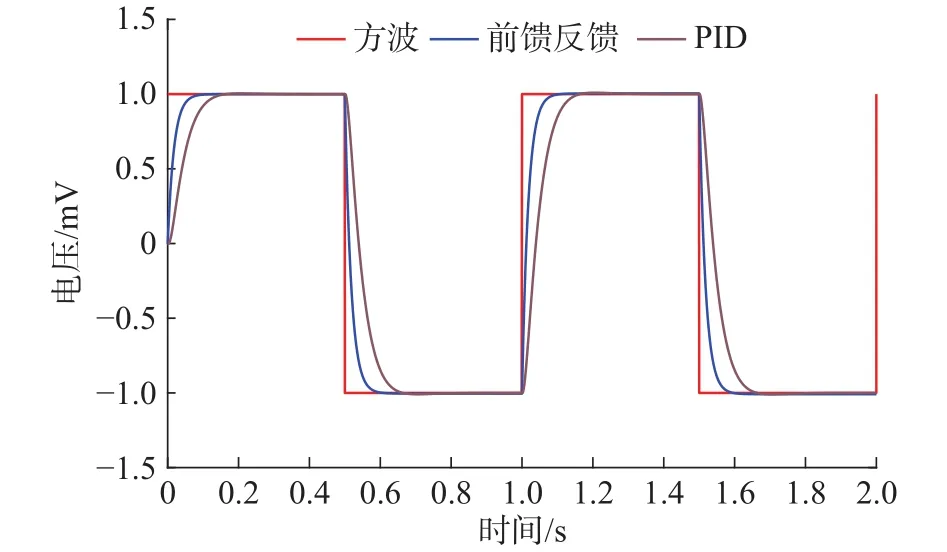
图13 闭环迭代正弦波跟踪曲线

由于系统容易受到高频信号的影响[17]，为了检验所设计的控制器在噪声的干扰下的鲁棒性，在正弦波预期输入里添加高斯白噪声信号。具体仿真结果如图14所示。

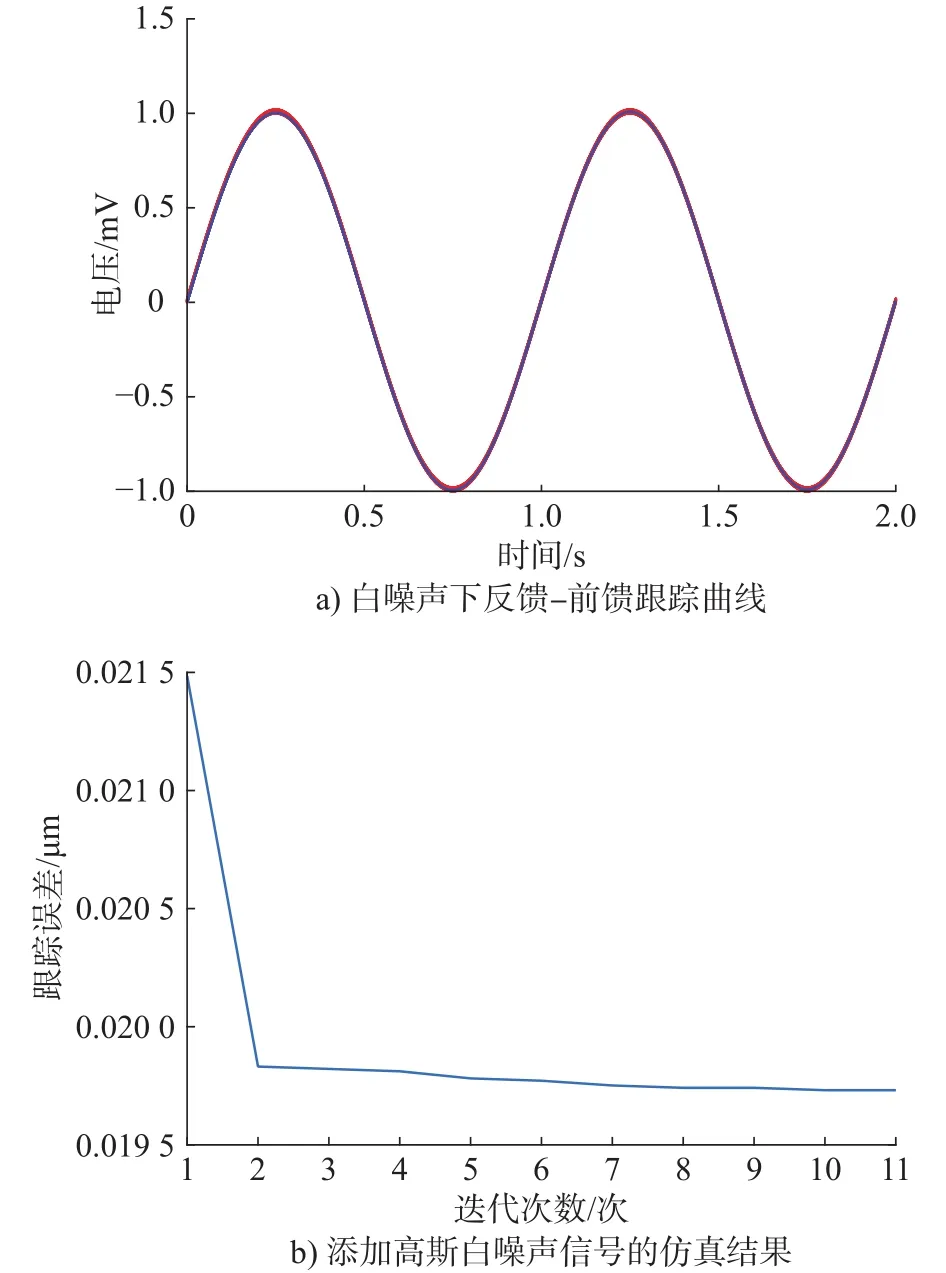
图14 添加高斯白噪声信号的仿真结果

通过比较可以看出，无论系统有没有白噪声输入，所设计的控制器最终都能使误差收敛到允许精度范围内，增加了系统的鲁棒性。

4 结论

通过系统的运行特征，将迭代学习引进微纳操纵成像系统中，对比3种学习律，选择了开闭环型，并在频域中证明了算法的收敛性。前馈开环迭代学习跟踪误差，反馈闭环迭代学习增强了系统的鲁棒性，并将传统的固定增益转变为指数变增益。通过频域最大幅值证明参数的收敛可行。通过仿真数据的对比分析，对于微纳操纵成像系统，反馈-前馈学习控制比PID控制以及单一学习控制更具有实际应用价值。[1]王一帆, 赵庆旭, 王盼, 等.微纳操纵成像系统自适应模糊PI控制器设 计[J].电光与控制, 2019, 26（4）:106-110