特征加权的高斯加权K近邻-支持向量机的水泵故障诊断方法
2022-04-19陈瑞杨春曦翟持龙超陈飞
陈瑞,杨春曦,翟持,龙超,陈飞
(1.昆明理工大学 化学工程学院,昆明 650500;2.昆明理工大学 机电工程学院,昆明 650500)
泵作为化工生产中分布范围广且数量较多的重要机械动力装置之一,在流体输送、转移和传质传热中具有重要作用[1-2]。因此对泵的工况进行实时检测和分析,及时发现其故障隐患并进行检修,可以大幅度提高泵的有效使用率,避免因泵故障而带来的安全隐患与经济损失。
泵体检测算法在近年来发展迅速,最常见的如支持向量机、贝叶斯网络、神经网络、智能算法优化分类算法等。1)基于支持向量机的泵体故障诊断:Rapur等[3]加入实时电流信号来辅助支持向量机对离心泵进行故障诊断和做到短期预测;Nikravesh等[4]使用不同小波提取滚动轴承振动特征信号导入支持向量机进行故障诊断,提高对故障类型识别的成功率。Zhang等[5]通过混合回溯搜索算法结合稀疏鲁棒最小二乘支持向量机提升对抽水涡轮泵模型参数识别率;孙斌等[6]使用等距特征映射降低数据维度来导入新核支持向量机中,用以提高转子故障诊断效果;宋涛[7]通过改进蚁群算法对改进最小二乘支持向量机进行参数寻优,提高对柱塞泵的故障诊断准确率。2)基于贝叶斯网络的泵体故障诊断,Cai等[8]使用贝叶斯网络对地源热泵进行多源信息故障诊断,验证模型对热泵多种故障进行诊断的准确率;Liu等[9]使用EEMD方法结合贝叶斯网络提升对齿轮泵故障诊断的准确率。3)基于神经网络的泵体故障诊断:张朝林等[10]通过CEMMD等与卷积神经网络结合,提取分解轴承故障特征数据,有效提高多工况下轴承的故障识别率;焦晓璇[11]运用神经网络算法结合Adaboost算法对机来提升对机载燃油泵故障诊断的准确率。4)智能算法优化机器学习算法在故障诊断、寿命预测应用广泛,除了上述出现的智能算法,常见运用的还包括遗传算法(Genetic algorithm)[12-14]、免疫算法(Immunealgorithm)[15-17]、模拟退火算法(Simulated annealing)[18-20]等。对于智能算法优化分类算法与单一分类算法的差异,Azadeh[21]使用人工神经网络、支持向量机、遗传算法优化支持向量机、粒子群算法优化支持向量机、决策树等算法对试验采集的离心泵故障数据进行了故障诊断效果对比,验证了遗传算法优化和粒子群优化支持向量机分类诊断效果更佳。
然而目前大多数文献所使用的数据均通过试验采集所得,虽然包含了泵体可能出现的所有故障的数据,但是总体数据量过小,不能真实反映泵在实际使用中所出现的故障分布情况。这里以化工厂实际采集数据为研究对象,针对化工厂水泵真实运行环境下的数据数量多、工况分布不均等情况,运用GWKNN-SVM融合算法对其进行诊断,仿真结果表明故障诊断准确率被明显提升。
1 水泵工况故障数据分析
以某化工厂型号分别为GBSS1、GBSS2、LSSB1的3台水泵作为研究对象,水泵的数据采集系统由电机转速传感器、振动加速度计、电机温度传感器组成。在2019年1 ~ 5月份中对泵体振动、电机振动、电机转速、电机温度这4个特征数据进行数据采集。工厂按照实际运行需求将水泵运行状态评定为A、B、C、D、E这5种工况,分别对应严重故障、较严重故障、中度故障、轻微故障和正常运行。由于工厂对严重故障采取自动停机机制,所以实际生产运行中3台水泵只收集到B、C、D、E这4种工况。以GBSS1号水泵为例,1 ~ 5月份共采集数据十万组。选取不同特征数据作为参考系,观察在三维分布环境下,数据实际的分布情况。由图1 ~ 图3可以明显观察到,BC、DE存在肉眼可见的相互聚类现象,其中聚类的工况数据在三维特征下又存在彼此不可分现象。具体表现为在不同特征维度下BC、DE之间数据分布间距较大,三维特征分布上存在明显的分隔区间,B与C、D与E之间却存在聚类现象。

图1 GSSB1 以电机转速、电机振动、水泵振动为坐标三维数据分布图

图2 GSSB1 以电机温度、电机振动、水泵振动为坐标三维数据分布图

图3 GSSB1 以电机温度、电机振动、电机转速为坐标三维数据分布图
针对数据所反映的工况分布特性问题,考虑充分利用K近邻算法能够对低特征数数据进行快速、高效地分类特点和支持向量机算法对小样本数据的高准确率分类优势,对高维数、大样本数据集中存在的部分重叠不可分数据高效准确地快速分类。
2 特征加权的 GWKNN-SVM 故障诊断模型
2.1 特征加权的高斯加权K近邻分类算法
传统KNN算法的思想可以描述为:对于已知的测试样本xt,在训练集中找出距离其最近的K个最近邻,然后根据K个最近邻的标签属性进行个数投票判决,得票最高属性为此测试点属性。距离一般采取是欧式距离,计算公式为
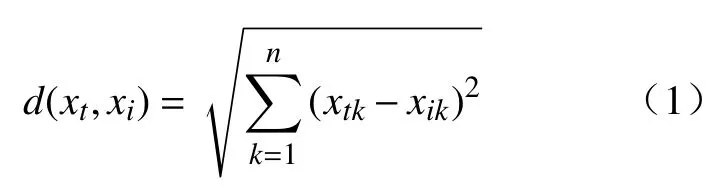
式中:k为计算维度;xtk、xik分别为xi、xt的特征值。
加权KNN算法是在传统KNN算法的基础上引入加权函数,将欧式距离远近问题转化为分布概率大小问题,常见的加权函数有反函数加权、减函数加权、高斯函数加权[22-23]等。本文选取高斯函数加权。
设L={(xi,ωi),xi∈Rd,i=1,2,···,n}为n个样本组成训练集, ωi为 每个样本xi的类别标签且类别已知,ωi∈ {ω1,ω2,···,ωr},xt为测试样本集,测试样本集的类别标签为 ωt。高斯函数加权实现的具体步骤如下:
1)数据归一化是将数据进行无量纲处理,将特征的数值的均落入 [0 ,1]区间内,以此来消除量纲带来的影响。归一化公式为

式 中 :x¯i、xij分 别 表 示 数 据 归 一 化 前 后 的 值 ;max(xij)、 m in(xj)分别表示每列特征的最大值和最小值。
2)使用欧式距离计算测试样本点xt到每个训练样本点xi的距离,即
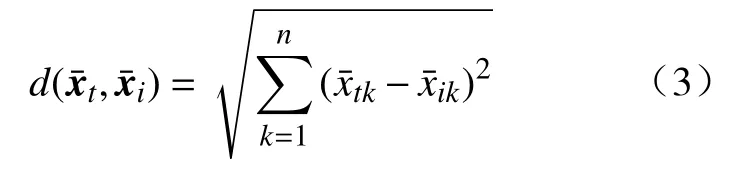
根据求出距离的大小,从训练集L中找出xt的最邻近的k样本点x1,x2,···,xk。

式中c=10。
4)根据xt的k个近邻样本,可以求出xt可能为ωs(s=1,2,···,r)类别的后验概率,即
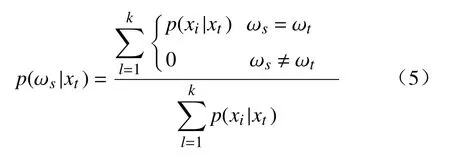
根据后验概率模型我们可以计算出的是最有可能的测试集分类属性值情况,即

式中GWKNN(xt)表示加权KNN分类器对待测样本xt的分类结果。
实际中数据的特征属性并不具有相同的影响因子,在泵体的故障诊断中,电机振动数据是广泛采用的,由于电机是泵体的关键部件,电机振动异常通常是泵体故障的关键因素。所以在已知的特征属性中选取特定特征属性赋予权值,提升其在数据中判定地位,从而提升故障诊断的准确率。本文选取电机振动特征进行加权值处理,权值公式为

式中:ai为电机振动,mm/s;bi为水泵振动,mm/s;ci为电机转速,r/min;di为电机温度,℃。
2.2 支持向量机原理
支持向量机是建立在统计学VC维理论和结构风险最小化基础上机器学习方法,在解决小样本、非线性、高维度数据中表现优异。
通过给定输入数据和分类目标: (xi,yi),xi∈Rm,yi∈ {+1,−1},i∈ (1,2,···,n)。超平面将目标类别按正类与负类分开,使得任意样本的点到平面距离大于等于1,已知超平面 (ω ·x)+b=0,其约束条件为

为了处理实际情况中的错分问题,继续在约束问题引入正松弛变量 ξi,约束条件修改为

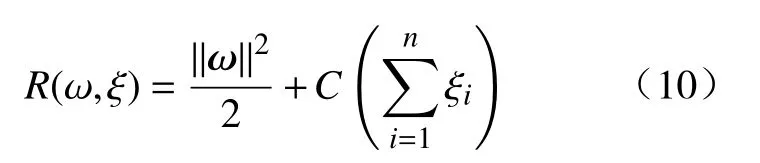
通过引入拉格朗日乘子 αi,得到拉格朗日函数表达式为

再通过对偶转换将式(11)转换为

之后通过训练样本求出上述最优解系数αio、ωo、bo,最后得出

对于非线性数据要引入核函数K(xi·x)代替xi·x。常见核函数包括线性核函数、多项式核函数、径向基核函数和Sigmoid核函数等,本文选择径向基核函数,其表达式为
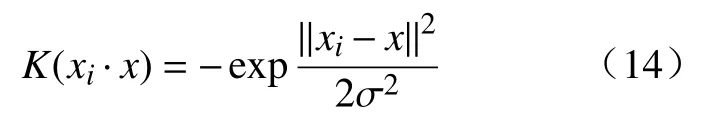
2.3 GWKNN-SVM水泵故障诊断模型
针对化工厂3台水泵在2019年1 ~ 5月份的实际运行情况中工况故障诊断问题,提出特征加权GWKNN-SVM融合算法。首先设定高斯分布概率阈值Yz,然后对水泵工况数据进行快速粗分类,计算出测试点的工况概率值P,统计最大概率值与之对应的工况结果,输出满足阈值条件数据YM分类结果。同时,调用接口函数将不满足阈值条件的数据YU继续导入支持向量机算法中进行进一步细分,最后整合全部YM与YU分类结果,从而达到提高整体数据的分类准确率的目的。基于特征加权GWKNNSVM融合算法故障诊断流程如图4所示。

图4 基于特征加权的GWKNN-SVM故障诊断算法流程图
特征加权GWKNN-SVM融合算法故障诊断具体分为以下步骤:
步骤1 将水泵数据预处理、归一化。
步骤2 对数据特征进行加权处理,引入权值Q。
步骤3 计算测试点分布概率P,统计各工况分布概率。
步骤4 统计最大分布概率和对应工况类别。判断最大分布概率数值是否达到设定阈值Yz大小。
步骤5 输出全部YM工况类别,储存结果至本地文件B1,全部YU数据,储存数据至本地文件B2。
步骤6 统计循环次数是否达到测试集样本数,达到次数至循环结束时接口函数调用SVM。
步骤7 重新调用样本集导入SVM分类器中。同时网格搜索最佳参数,进行训练分类。
步骤8YU数据导入训练完成的SVM分类器,输出全部工况类别,储存工况结果至B3。
步骤9 调用B1和B3文件,统计函数根据序号整合YM与YU分类结果,统计测试数据工况分类情况。
步骤10 验证统计输出算法最终准确率。
需要注意的是,阈值设置不能过低或过高,否则所有数据只会进入单一算法,降低算法准确率。
3 仿真试验
3.1 试验数据与参数
仿真第一组试验为GSSB1水泵1 ~ 5月运行数据,对5个月份数据进行降噪处理后,随机分成3个数据量不同的对比组,3个数量组分别为四万组数据、六万组数据、八万组数据,验证模型在多工况、不同数据量级下分类效果。仿真第二组数据为GSSB2号水泵 4 ~ 5月份 B、C两种工况数据,仿真数据第三组为LSSB1水泵3 ~ 4月份D、E两种工况数据,验证模型对不同水泵数据的分类效果。
表1为不同水泵不同工况下其采集特征数据表,以电机振动(mm/s)、水泵振动(mm/s)、电机转速(r/min)、电机温度(℃)为主要4个特征参数。表2为不同试验组特征权值和网格搜索得到的支持向量机算法参数、核函数、多分类模型。表3为水泵工况类型对应的故障表现及原因。

表1 水泵工况类型数据表

表2 权值及 SVM 训练参数

表3 水泵工况故障表现及原因
3.2 试验结果与讨论
本文采用对比试验来确定特征参数的权值。以GSSB1-8试验组的权值选取为例,该组权值的选择步骤为:首先选取相同K值环境下运行(本次试验K= 11),然后算出原 GWKNN 算法准确率为91.16%。而特征加权GWKNN算法在0 ~ 1权值变化如图5所示。加入权值后明显可以观察到特征加权的引入对准确率有了提升作用,通过对比可知,本组试验组在权值为0.7时,准确率提升到91.66%,因此该权值为最佳权值。同理,通过对比试验确定其余4组试验数据集的特征权值。
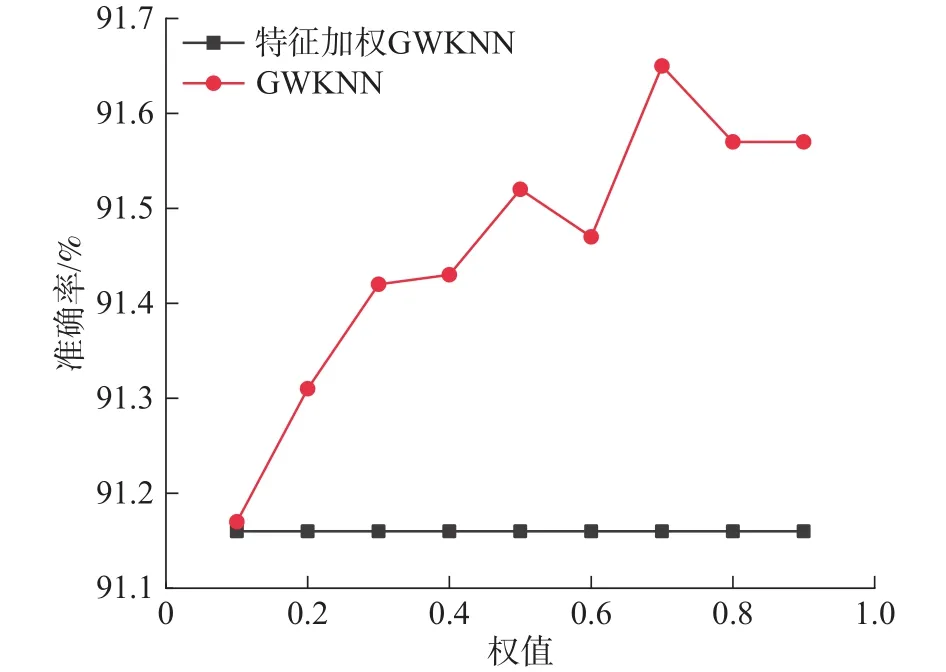
图5 GSSB1-8 权值选取准确率对比图
为了验证GWKNN-SVM算法故障诊断效果,选取了5组不同对比试验组,通过与KNN算法和SVM算法对5组试验数据进行故障诊断的准确率来进行对比。试验数据组一、二、三是提取GSSB1号水泵在 1 ~ 5月份中具有 B、C、D、E这4类工况都存在的运行数据,根据每种工况在总样本集中的占比率大小来从中选取了3组不同数量级的样本集。这3组试验数据集分别用GSSB1-4、GSSB1-6、GSSB1-8表示,来模拟实际化工厂运行环境下水泵各类工况数据分布情况,用以验证数据工况在不同数量级下对算法的影响程度。试验组四是提取GSSB2号水泵在3 ~ 4月份中具有B、C两类工况相互变化数据,试验组五是提取LSSB1号水泵在4 ~ 5月份中具有D、E两类工况相互变化数据,用以验证在实际运行环境下不同水泵不同工况对算法准确率的影响。试验采用评估指标TPR(True possitive rate),其表达式为

式中:TP实 际为正类,预测也为正类;TN实际为负类,预测也为负类;FN实际为正类,预测为负类;FP实际为负类,预测为正类。
如图6 ~ 图8所示,特征加权GWKNN-SVM算法对GSSB1号水泵不同数量级数据故障诊断效果可知,GWKNN算法相对于传统KNN算法随着数量级的提升,其准确率的提升趋于稳定。特征加权GWKNN-SVM算法对GSSB1-4故障诊断效果相比传统SVM算法平均准确率提升1%、相比传统KNN算法平均准确率提升2%,GSSB1-6故障诊断效果相比传统SVM算法平均准确率提升1.5%、相比传统KNN算法平均准确率提升1%,GSSB1-8故障诊断效果相比传统SVM算法平均准确率提升1%、相比传统KNN算法平均准确率提升1.8%。从图中K值的变化中可知,GWKNN-SVM算法对K值的变化不敏感,所以具有较强适应性。

图6 GSSB1-4 不同 K 值下的准确率

图7 GSSB1-6 不同 K 值下的准确率
同时,为了验证融合算法的通用性,这里提取LSSB1号水泵与GSSB2号水泵在实际运行中两个月数据中出现的工况类别进行对比,即LSSB1号水泵3 ~ 4月份中出现D、E两种工况类别,GSSB2号水泵4 ~ 5月份中出现 B、C两种工况类别,如图9和图10所示。
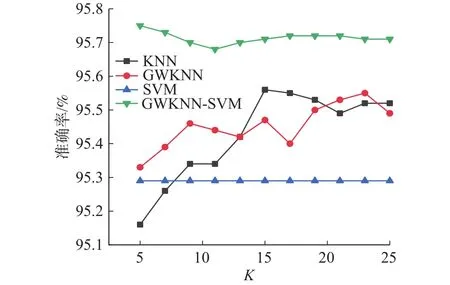
图9 LSSB1 水泵 3 ~ 4 月份不同 K 值下的准确率

图10 GSSB2 水泵 4 ~ 5 月份不同 K 值下的准确率
图9中GWKNN算法相比KNN算法的准确率随着K值变化有波动变化。特征加权GWKNNSVM算法则优于其它3种算法,而SVM算法准确率最低。在图10中GWKNN算法相比KNN算法在不同K值变化下都明显提升4.2%,相比SVM提升1%,特征加权GWKNN-SVM相比于SVM提升1.75%。综上所述,特征加权GWKNN-SVM算法在不同水泵、不同月份、不同工况情况下故障诊断的准确率都具有明显提升。
表4为本文算法与其他分类算法在3台水泵数据集上进行准确率对比试验,验证本文算法与其他常用分类算法(NB为朴素贝叶斯算法、ANN为人工神经网络算法、GA-SVM为遗传算法优化支持向量机)在不同水泵工况数据诊断能力。试验结果表明,本文算法对不同运行环境下的工况诊断能力均优于其他对比算法。
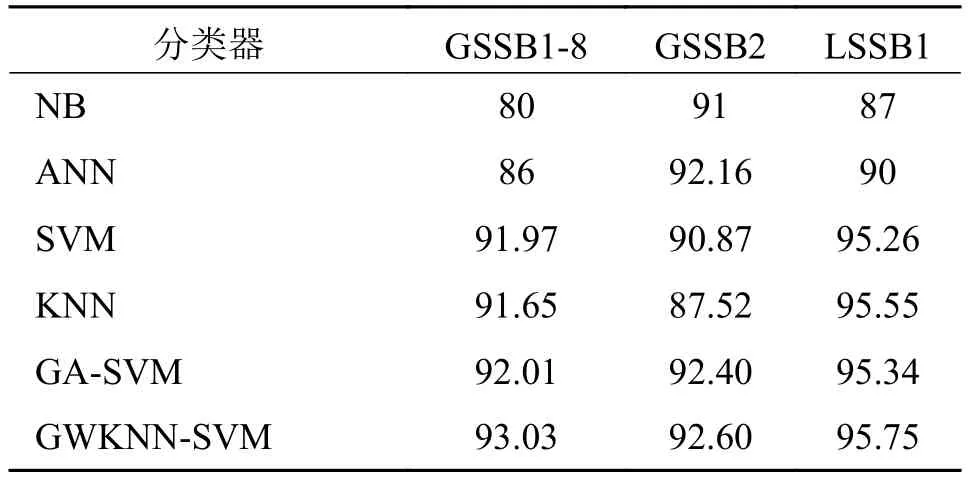
表4 不同分类器准确率结果对比表 %
4 结论
为有效地对工业水泵故障数据进行诊断处理,本文提出基于特征加权的GWKNN-SVM水泵故障诊断方法。试验结果表明该方法能够有效提高故障诊断效率,通过试验分析与验证,得到以下结论:
1)通过对水泵电机振动这一特征数据进行加权处理,再结合高斯加权KNN算法,可以有效提升故障诊断的准确率。
2)提出的基于特征加权GWKNN-SVM故障诊断融合算法,与其他分类算法相比,能够有效提升对水泵工况故障诊断的准确率和可靠性。
3)在数据分析过程中,有部分数据未能正确分类出来的原因在于B、C和D、E相互之间转换的边界数据模糊,目前四维特征参数环境下无法得到清晰的分类边界,应通过增加压力、流量、电流等其他特征参数来提升工况之间数据差异性,从而提高分类准确率。
