基于Hydrus-1D的黄河泥沙充填复垦土壤夹层结构优化

王晓彤，胡振琪，梁宇生

（1. 北京大学城市与环境学院，北京 100080；2. 中国矿业大学环境与测绘学院，徐州 221116；3. 中国矿业大学（北京）土地复垦与生态重建研究所，北京 100083）

0 引 言

黄河流域分布有宁东、神东、陕北、晋北、晋中、黄陇、晋东、河南、鲁西9大煤炭基地，涉及58个全国规划矿区，总面积约为13.62万km。煤炭开采后，在滨黄河矿区产生了大面积的采煤沉陷地甚至积水区，生态修复任务艰巨。采用黄河泥沙充填复垦采煤沉陷地，既疏浚了黄河下游淤积的泥沙，又实现了土地的综合整治，具有显著的社会及生态效益。目前，黄河泥沙充填复垦采煤沉陷地常采用一次性充填技术，形成“上土下沙”土壤剖面构型。采用该技术复垦后的土壤漏水漏肥，农作物单产低，然而在黄河泥沙充填层中夹土壤层后，能有效提高农作物产量。土壤水分是影响植被生长的重要因素之一，是恢复重构土壤耕作水平的基础。土壤剖面构型由简单到复杂的改变，有效改善了土壤水分的运动过程。

国内外对于层状土壤水分运动的研究，多采用入渗与蒸发试验，多集中于研究夹砂层、不同土层排序、覆盖层厚度等对土壤水分特性的影响。王春颖等通过室内入渗试验对具有夹砂层结构的土体进行研究，结果表明基质吸力较大的砂夹层能够促进土壤水分的入渗。李毅等通过研究不同夹砂层位置（5～10、10～15、20～25 cm）对水分入渗的影响，结果表明夹砂层的存在改变了土壤的入渗率，且夹砂层位置越深，对入渗率的改变越明显。Romano等提出不同土层排列顺序能够影响土壤水分的再分布及土壤的持水能力。Si等进行田间试验研究分析发现层状土壤在降低土壤水分下渗速率的同时，田间持水量得到有效提高。Huang等通过对层状土壤水分蒸发及再分布过程研究表明，不同类型层状土壤结构的水分蒸发特性不同。宋日权等通过对上覆砂土结构的研究表明，对于层状土壤结构，砂夹层对土壤水分蒸发影响较大。

已有研究采用室内入渗、蒸发试验证明了黄河泥沙夹层式土壤剖面构型能够改善上土下沙土壤剖面构型的水分特性，并通过室内入渗试验进行了关于黏土夹层位置对黄河泥沙填复垦土壤水分入渗过程影响的分析。然而物理模拟试验存在人力、物力及时间等的局限性，近年来相关软件的开发应用为描述土壤水分运移提供了有利的工具。其中，Hydrus软件采用有限元法求解，以Richards方程为基础，能够为研究者提供一种快速准确的方式模拟土壤水分的运移过程，因其模型边界条件灵活，在不同结构和不同质地土壤水分运动的相关研究中得到了较为广泛的应用。王成文、肖庆礼等验证了Hydrus-1D模拟不同结构和质地的土壤水分运动的适应性。范严伟等模拟了夹层质地、埋深、厚度、压力水头及初始含水率对入渗特性的影响。Wang等模拟了黏土中夹砂的层状土壤入渗特性，证明了粗质夹层能够促进入渗。Wang等模拟了具有不同斥水性及不同夹层位置的土壤剖面构型的水分特性，结果表明夹层的斥水性相对于夹层位置而言作用更显著。Jia等通过Hydrus-1D拟合分析了由砒砂岩和风沙土构建的不同结构的重构土体对水分运动参数的影响。吴奇凡等利用Hydrus-1D模拟分析了由沙土、砒砂岩、黄绵土和红黏土构成的不同结构层状土的入渗特征，结合晋陕蒙接壤区自然条件，评价适合排土场建设的层状土体。

目前，国内外针对自然农业土壤和重构土壤的土层覆盖顺序、砂夹层结构等的水分运动机理的研究较多，而对于黏土夹层对重构土壤水分运动的影响研究甚少。另外，数值模拟方法在国内外各个领域得到了广泛的应用，然而采用数值模拟分析不同夹层结构的土壤水分运动并指导黄河泥沙充填复垦土壤剖面优化设计有待探究。相关研究表明在一次性充填复垦后覆盖土层厚度达到70 cm才能满足玉米生长的基本需求。然而，在某些土壤资源紧缺的矿区，该技术的推广应用受限。本研究采用实测试验优化的模型参数，建立Hydrus土壤水分运动模型，以复垦土壤总厚度60 cm为例，综合考虑夹层厚度、位置和数量的交互作用，进行模拟剖面设计，模拟分析具有不同夹层结构的黄河泥沙充填复垦土壤的水分入渗和蒸发特性，以期为黄河泥沙夹层式土壤剖面优化设计提出一种经济时效的方法。

1 材料与方法

1.1 试验材料

试验材料包括表土、心土和黄河泥沙。表土（0～20 cm）和心土（>20～60 cm）均采自山东省德州市齐河县邱集煤矿采煤沉陷地（36°28′52″N，116°28′03″E）。黄河泥沙采自山东省德州市齐河县邱集靳庄引黄干渠（36°29′40″N，116°28′54″E），距采煤沉陷地1.89 km。样品采集运回实验室后，在晾晒板上风干后，经碾压、磨碎、过2 mm筛，分别混合均匀后备用。表土、心土和黄河泥沙的容重用环刀法田间实测获得，分别为1.35、1.43、1.50 g/cm；颗粒组成采用吸管法测定，表土质地为粉黏壤含黏粒20.43%、粉粒70.16%、砂粒9.42%，心土质地为黏土，含黏粒62.54%、粉粒33.16%、砂粒4.3%，黄河泥沙质地为壤砂土，含黏粒20.43%、粉粒70.16%、砂粒9.42%；初始含水率和饱和含水率均采用时域反射（Time-Domain Reflectometer，TDR）并结合烘干法进行校准对比获得，初始含水率分别为0.067、0.083、0.024 cm/cm；饱和含水率0.48、0.49和0.42 cm/cm；饱和导水率采用定水头渗透筒法测定，分别为0.011、0.004和0.160 cm/min；水分特征曲线采用压力膜法测定，如图1所示。

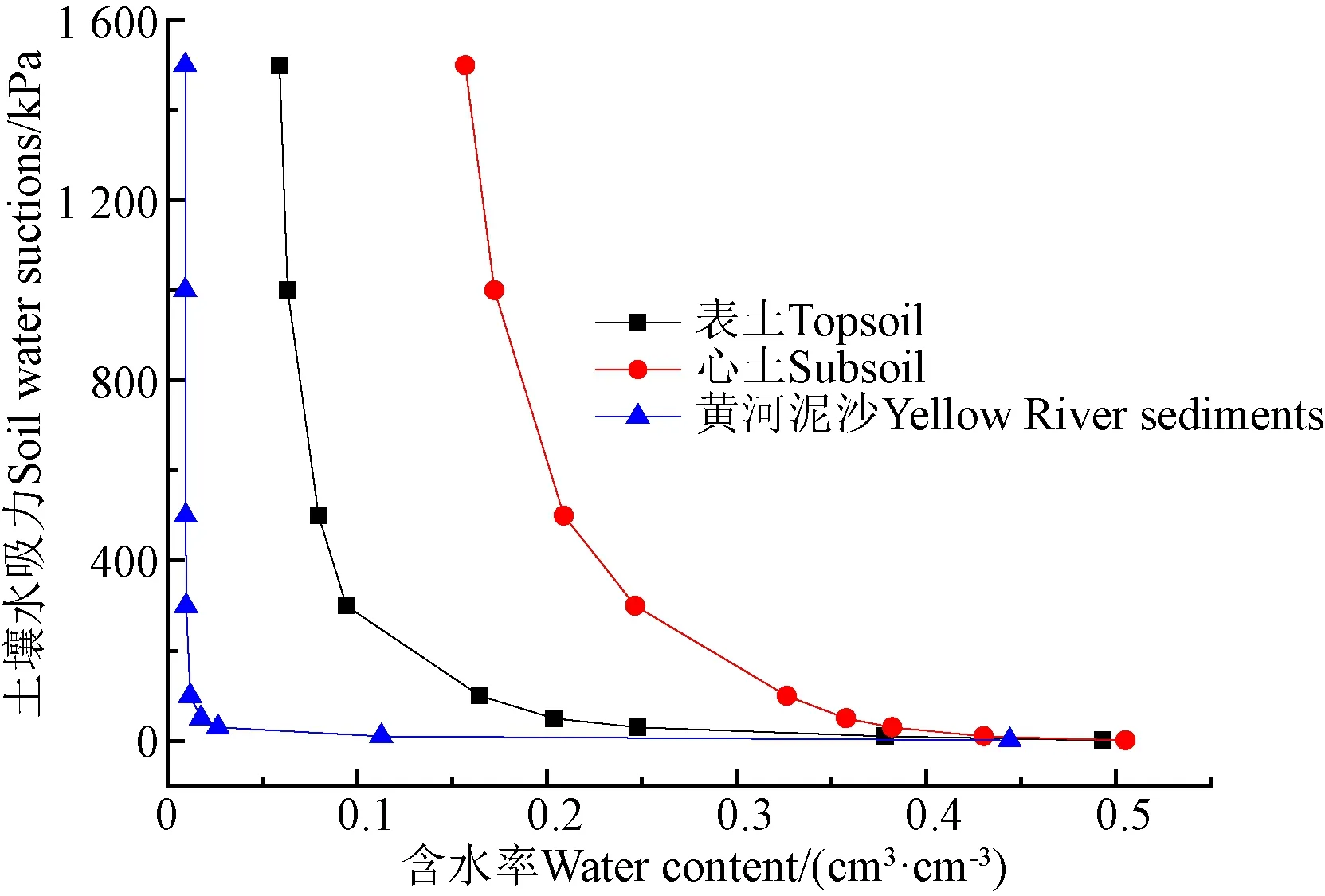
图1 土壤水分特征曲线 Fig.1 Soil water characteristic curve

1.2 实测试验设计

实测试验用以确定模型参数，并证明优化后的模型参数能够较好地模拟黄河泥沙充填复垦所形成的全土、上土下沙及夹层式土壤的水分运动特性。实测试验剖面共设计3个处理，如图2所示，每个处理设置3个重复。其中，a.全土表示未损的农田土壤剖面构型，是由20 cm厚的表土层覆盖在100 cm厚的心土层上构成；b.上土下沙表示黄河泥沙一次性充填复垦所形成的土沙双层剖面构型，由20 cm表土层及20 cm心土层依次覆盖在黄河泥沙充填层上构成；c.夹层式表示在黄河泥沙充填层中夹心土层形成的夹层式土壤剖面构型，黄河泥沙充填层中夹20 cm心土夹层并由20 cm表土层及20 cm心土层依次覆盖后构成。

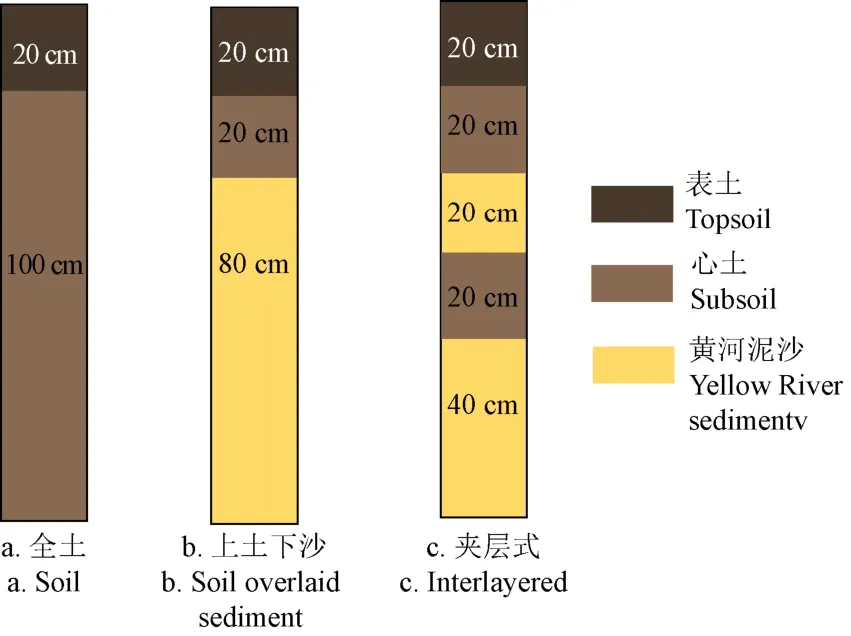
图2 实测试验土壤剖面示意图 Fig.2 Diagram of different soil profiles for measured experiment

试验过程分为入渗和蒸发两个阶段，试验装置如图3所示。有机玻璃管内径为19 cm，高为130 cm（填装土柱高度为120 cm）。根据表土容重为1.35 g/cm、心土容重为1.43 g/cm、黄河泥沙容重为1.50 g/cm，按每层5 cm称取相应质量进行分层填装，层间打毛。各处理均在10、30、45、55、75、85、95、105及115 m插水分传感器EC-5。土柱填装完成后，土表覆盖滤纸，静置48 h。调整马氏瓶的高度，保持恒定水头3 cm，开始入渗试验。试验按照时间由密到疏，记录湿润锋的位置及通过马氏瓶读取累积入渗量，同时设定数据采集器步长为5 min自动记录土壤水分传感器探头处土壤含水率随时间的变化。直至湿润锋到达土柱最底部，停止马氏瓶供水，入渗试验结束。

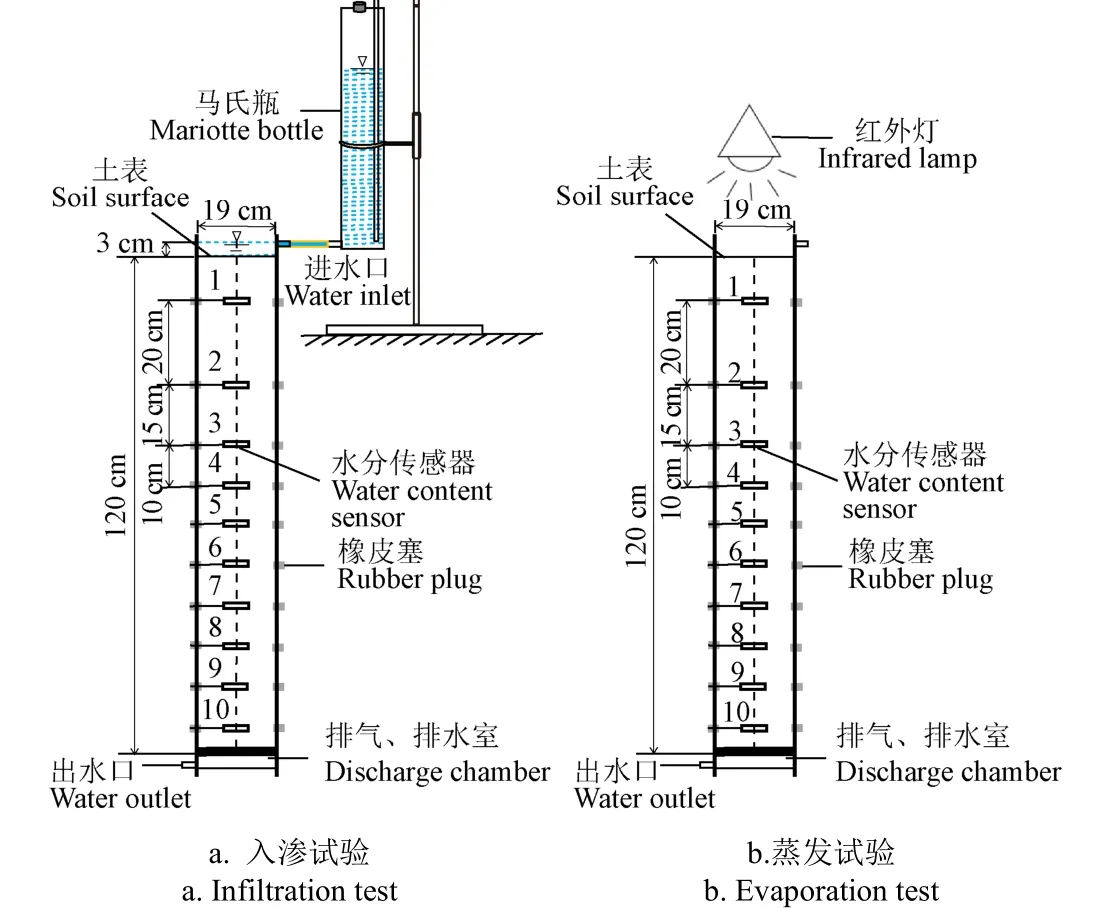
图3 试验装置 Fig.3 Experimental devices

蒸发试验在入渗试验完成后进行。首先称取每根土柱的质量，然后将土柱置于275 W灯下30 cm处。室温维持在24.5±0.5 ℃，相对湿度保持在25%～30%左右。光照时段设置为每天早上8:00到下午17:00，平均日蒸发量为0.94 cm/d。蒸发过程中数据采集器的测量时间步长设定为30 min，自动记录土柱每层含水率随时间变化状况。蒸发过程持续30 d，每天17:00 称取土柱质量。

1.3 模拟试验设计

采用实测试验优化后的模型参数，根据沉陷区的实际情况，综合考虑夹层厚度、位置和数量的交互作用，进行模拟剖面设计，通过Hydrus-1D模拟与正交试验分析，探明不同夹层处理对土壤水分运动影响，实现夹层式剖面的优化设计。本研究以沉陷区可供利用的土壤总厚度60 cm为例，综合考虑夹层式复垦的技术可实践性及各因素间的相互作用，并参考任露泉编著的《试验优化设计与分析》，以黄河泥沙充填层中土壤夹层的厚度、位置、和数量为试验因素，每个因素选取2个水平，不同夹层厚度20和30 cm，不同夹层位置（所在黄河泥沙充填层中的位置，即为第一层黄河泥沙层的厚度）为20和30 cm，不同夹层数量为1层和2层，因素水平表如表1所示，正交试验设计见表2。

表1 因素水平表 Table 1 Levels of factors

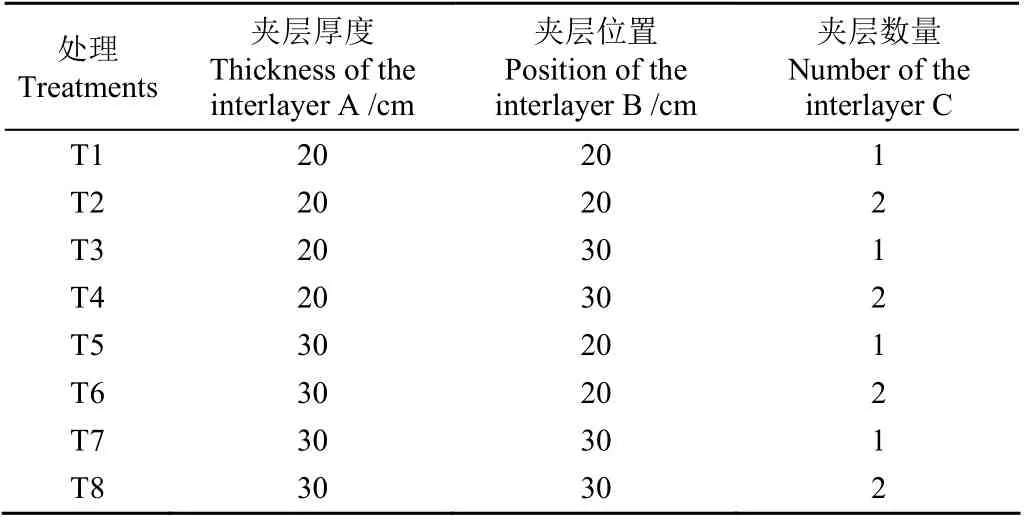
表2 正交试验设计表 Table 2 Orthogonal experimental design table

依据国家土地复垦质量控制标准（TD/T 1036-2013）并结合黄河泥沙充填复垦工艺，选定120 cm土层厚度作为模拟土壤入渗和蒸发试验土柱长度。模拟试验共设计8个处理，如图4所示。CK1为未损毁的农田土壤剖面构型，CK2为一次性充填黄河泥沙后覆盖土壤层形成的上土下沙土壤剖面构型。T1～T8为黄河泥沙夹层式土壤剖面构型，依据正交表L8（2）设计得到。在确定模型参数的基础之上，利用Hydrus-1D模型模拟研究不同土壤剖面构型中的土壤水分入渗和蒸发特性，依据可供利用土源数量，因地制宜为采煤沉陷地优选黄河泥沙充填复垦土壤剖面构型。

图4 模拟试验土壤剖面示意图 Fig.4 Diagram of soil profiles for simulation test

模拟垂直一维土壤入渗和蒸发过程，可选用一维的Richards方程作为土壤剖面水流运动的控制方程。

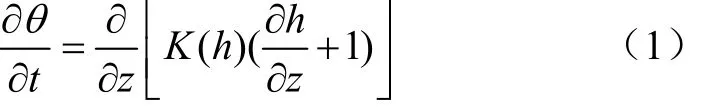
式中为垂向坐标，规定向上为正，cm；为基质势，cm；为时间，min（入渗）或d（蒸发）；为土壤含水率，cm/cm；土壤导水率，cm/min（入渗过程）或cm/d（蒸发过程）。

式（1）中涉及非饱和土壤水力特性()和()采用van Genuchten方程表示，van Genuchten运用Mualem孔径分布模型得到非饱和导水率函数的预测方程。脱水时，某一基质势对应的含水率比吸水系统的含水率高，因此在蒸发过程中的水分运动存在一定的滞后现象。

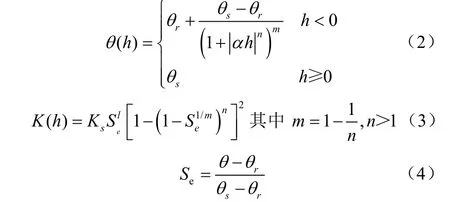
式中θ为滞留含水率（吸水过程用θ 表示，脱水过程用θ 表示），cm/cm；θ为饱和含水率，cm/cm；（吸水过程用α表示，脱水过程用α表示）为进气吸力的倒数、为土壤的孔隙体积大小分布指数；为 VG 方程参数；反映了土壤孔隙的连接性，通常取值为0.5；K为饱和导水率，cm/min（入渗过程）或cm/d（蒸发过程）；S为无量纲的有效水分含量。

入渗试验初始条件假定每层土壤初始含水率均匀分布，根据表土、心土、黄河泥沙的初始含水率分别计算每层的基质势。

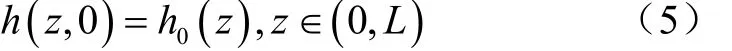
式中为模拟土柱的长度，cm；根据初始含水率计算所得的基质势；向下为正方向，=0为土表，cm。

入渗试验边界条件为上边界水头值为3 cm，入渗试验土柱为120 cm，模拟地段山东省德州市齐河县平均地下水位在200 mm左右。本研究中不考虑地下水位对土壤水分运动过程的影响，因此下边界自由排水。

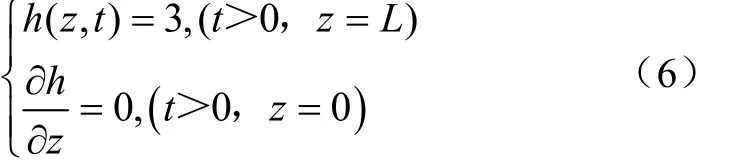
式中()为蒸发通量，cm/d；()为初始状态的土壤剖面含水率，cm/cm；上界面大气蒸发量计算公式如下所示

式中E=()为土表的实际蒸发率，cm/d；E为土表的潜在蒸发速率，cm/d，其采用直径为20 cm蒸发皿测定潜在蒸发量，蒸发皿与土柱表面离红外灯的距离相同。h为表表最小水势值，cm。

Hydrus-1D在进行数值求解的过程中采用有限差分法，因此需要对模型进行时间和空间的离散化处理。时间离散设计的合理性，与数值模型计算的收敛性、计算的速度和计算的稳定性密切相关。参考物理模拟试验过时间分布情况，入渗过程最终时间设定为6 000 min，初始时间步长为0.1 min，最小步长为0.000 1min，最大时间步长为120 min，输出时间点数量为50个。蒸发过程最终模拟时间为30 d，初始时间步长为0.01 d，最小时间步长为0.000 1 d，最大时间步长为1 d，输出时间点数量为30个。空间离散设计中，土壤剖面模型深度为=120 cm，土壤的种类分为三种，根据图1进行不同处理土壤剖面建模。首先对土壤剖面进行离散化，为了分层方便设定剖面节点为121个，空间步长为∆=1 cm。

2 结果与分析

2.1 模型参数的确定

首先，对反演的模型参数进行赋初值，饱和导水率K及饱和含水率θ通过实测获得，θ、、依据实测均质表土、心土和黄河泥沙的水分特征曲线，利用van Genuchten模型进行相应水力参数进行拟合获得，其中饱和含水率采用实测值。模拟结果表明，通过水分特征曲线拟合获得的水力学参数，模拟效果不佳，不同处理入渗与蒸发过程的剖面含水率实测与模拟值相对误差较高，在20%左右。其主要原因是由于层状土壤的水分运动过程较均质土壤存在较大的差异。为解决误差较大的问题，采用入渗实测土壤剖面含水率随时间的变化反演土壤水力参数是可行性的。

根据实测全土、上土下沙及夹层式重构土壤入渗和蒸发试验剖面含水率的动态变化数据，反演求解土壤水力参数，并结合湿润锋、累积入渗量及累积蒸发量等指标进行反复率定。优化后的水力参数，模拟效果良好，不同处理入渗与蒸发过程剖面含水率实测与模拟值相对误差降低到10%以内。土壤水力参数优化值如表3所示。其中，饱和导水率K实测与优化值存在较大的差异，不同材料的导水率均得到了不同程度的减小，尤其是黄河泥沙的导水率缩小至1/8，其原因是由于装土过程中黄河泥沙的容重不易控制，导致层状结构土壤不同层位黄河泥沙的饱和导水率与均质土壤实测饱和导水率存在较大的差异。Huang等在模拟非均质土壤水分入渗时，也得出了类似的结论，假定K为最大的误差源，不确定性远大于θ、θ、，把K作为校验变量，取得较好的模拟结果。在土壤水分运动过程中吸水和脱水过程中存在的滞后作用是不可忽略的，通常采用α、θ 表示吸湿过程，采用α、θ 表示脱湿过程。有学者研究表明，可允许土壤水分入渗和蒸发过程中水力参数θ、K、保持一致，通过不同取值α、θ 和α、θ 进行区分，可在一定程度上简化模型的计算。

表3 土壤水力参数优化值 Table 3 Optimized values of soil hydraulic parameters

全土、上土下沙及夹层式重构土壤的累积入渗量、湿润锋及累积蒸发量的实测值与模拟值如图5所示，通过对比发现，优化后的参数总体模拟效果较好。各处理累积入渗量和湿润锋的模拟值总体略高于实测值，累积蒸发量的模拟效果最佳。优化后的水力参数模拟效果评价指标中均大于0.997，RRMSE均小于0.167，NSE均大于0.912（NSE值越接近1，表示模型可信度高），模拟效果较好。其中，各处理湿润锋的模拟值与实测值偏差稍大，主要原因是由于Hydrus-1D对于湿润锋模拟判断的敏感度稍差一点。

在初始水权划定之后，就要把水权作为产权对待，保护水权的合法权益。水权不能被随意剥夺或变更，水权所有者拥有水权的收益权、处置权。对于水权所有者节水节省的水量，不但允许用户获得水费节约收益，还应当允许其出售水权而获得收益。

图5 累积入渗量、湿润锋和累积蒸发量实测值和模拟值 Fig.5 Observed and simulated value of cumulative infiltration, wetting front, and cumulative evaporation

2.2 夹层对水分入渗的影响

入渗阶段各处理累积入渗量和湿润锋随时间的变化如图6所示。CK1累积入渗量随时间的变化为非线性关系，整个过程中入渗率随时间的增加而逐渐减少。其余处理在湿润锋穿过上覆表土和心土层后，累积入渗量曲线发生转折而后随时间呈线性变化。对于T1～T8，由于黄河泥沙层中心土夹层的存在，湿润锋的运移曲线将发生多次转折。在湿润锋未到达第一个“沙-土”界面前，由黄河泥沙的基质势较高而心土层中的基质势较低，泥沙初始状态所含的水分会逐渐向心土层中转移，直至湿润锋到达“沙-土”界面，此时黄河泥沙中的基质势随含水率的增加而迅速增加，但由于大毛管接在小毛管之上形成了一定的毛管障碍，导致水分在上界面处聚积，造成基质吸力值的波动。与心土夹层上界面不同的是湿润锋运移至“土-沙”界面处，由于小毛管较大毛管的吸力大，在基质吸力的作用下，湿润锋的运移会出现短暂的停顿。此时，心土层的含水率因吸收了黄河泥沙中的水分而增加，当土壤水分在穿越“土-沙”界面后，湿润锋的运移速率将迅速增大，这一规律与王春颖等的研究较为符合。由于夹层式土壤剖面处理中夹层位置、厚度和数量不同，对累积入渗量的影响程度亦不相同。当湿润运移至土柱底端120 cm时，CK1、CK2及T1～T8累积入渗量分别为45.17、37.48、39.69，40.18、40.53、40.56、40.39、41.60、41.77和42.24 cm。CK2的累积入渗量最低，入渗过程中土壤持水能力差。T1～T8入渗过程的持水量较CK2分别提高了5.98%、7.29%、8.22%、8.30%、7.85%、11.08%、11.54%和12.79%，说明夹层厚度、数量和位置的增加，均能在一定程度上提高重构土壤入渗过程的持水量。

图6 模型模拟各处理累积入渗量和湿润锋 Fig.6 Cumulative infiltration and wetting front of each treatment simulated by the model

入渗阶段各处理剖面含水率随时间的动态变化模拟结果如图7所示。CK1的土壤剖面含水率分布比较均匀，与其相比，黄河泥沙重构土壤入渗过程较为复杂，重构土壤剖面含水率分布具有不连续的特性。CK2的剖面含水率高低分层明显，由于入渗过程中覆盖的土壤层含水率随湿润的推进很快达到饱和，而下层黄河泥沙的含水率较低，在整个入渗过程中一直处于非饱和的状态。将CK2覆盖土壤层的一部分心土作为夹层，所形成的黄河泥沙夹层式土壤剖面构型（T1～T8），因黄河泥沙充填层中心土层的存在，形成了不同程度的水流障碍，有效提高了心土层上方黄河泥沙层的含水率，随着湿润锋的推进甚至能够达到饱和。Hammecker等在进行层状土壤入渗试验的研究中，同样发现表层土壤达到饱和而砂土层的土壤处于非饱和的状态。Cui等研究表明，导致这一现象的原因是上层较细的土壤对下层较粗的土壤起到了一定的水分下渗限制作用。夹层式剖面构型中，通过设置在泥沙层中的观测点可以看出，心土层上方的泥沙层含水率曲线均出现两次上升的现象，说明由泥沙层中大孔隙的存在出现优先流，使得一部分泥沙优先湿润，然而由于其下方心土夹层的存在，形成了一定的阻水障碍，导致水分在其“沙-土”界面上方聚积，造成了泥沙层的二次湿润。Wang等研究发现了类似的现象，认为其原因是因为湿润峰在分层界面处暂时停止，而入渗过程仍在继续进行，因此水分向上再次湿润砂土层。

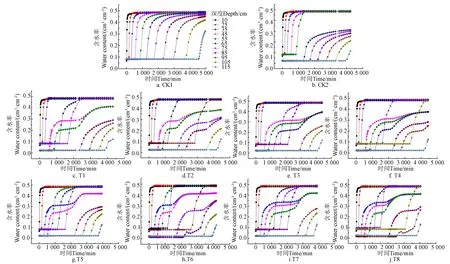
图7 入渗阶段各处理不同深度剖面含水率随时间的变化 Fig.7 Change of water content in different depth profiles of each treatment at infiltration stage

2.3 夹层对水分蒸发的影响

各处理累积蒸发量的模拟结果如图8所示，累积蒸发量在蒸发的第一个阶段主要受到大气蒸发强度的影响，大量的土壤水分因蒸发而损失，各处理变化较为一致。差异主要出现在蒸发的第12天，CK1率先进入蒸发的第二个阶段，随后T1～T8相继进入蒸发的第二个阶段，累积蒸发量随时间的变化逐渐趋于稳定。而CK2累积蒸发量随时间变化呈线性关系的持续时间最长，最晚进入蒸发第二个阶段的。对比发现夹层式剖面构型（T1～T8）的累积蒸发量曲线均介于CK1和CK2之间。蒸发至第30天，CK1的累积蒸发量最低为17.14 cm，CK2的累积蒸发量最高为20.16 cm，在相同蒸发条件下，累积蒸发量较CK1高出18%。说明黄河泥沙充填复垦上土下沙土壤剖面构型促进了土壤水分的蒸发，不利于水分的保持。夹层式土壤剖面构型（T1～T8）较CK2的累积蒸发量分别较低了5.10%、5.34%、4.52%、4.43%、10.09%、9.51%、8.96%、7.57%，说明夹层厚度的增加能够有效抑制土壤水分的蒸发。李韵珠等研究得出了类似的规律，黏土夹层愈厚则蒸发速率愈低。

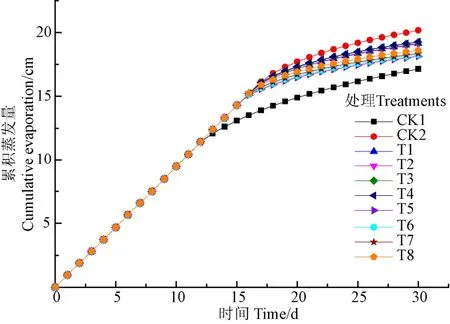
图8 模型模拟各处理累积蒸发量 Fig.8 Cumulative evaporation of each treatment simulated by the model

蒸发阶段各处理土壤剖面含水率随时间的动态变化规律如图9所示。蒸发初期存在土壤剖面的内部排水过程，水分在土水势的作用进行重新分配，下层的土壤含水率会明显提高，变化最大的是115 cm处的观测点，该层位处含水率在短时间内迅速增加，而后随蒸发进行逐渐减少。CK1在蒸发过程中 10 cm土层处的水分蒸发量最大，说明该构型水分蒸发主要来源于表土层，其心土层水分分布比较均匀，含水率在 0.30～0.35 cm/cm之间维持稳定。CK2在蒸发过程中表土层、心土层和黄河泥沙层的含水率的分层较为明显。在蒸发的前15 d左右，表土层和黄河泥沙层的含水率迅速减少，而心土层由于得到来自于黄河泥沙层的水分补给，含水率降低缓慢；蒸发进入第二阶段，表土和黄河泥沙中的含水率逐渐稳定，而心土层的含水率开始逐渐降低。T1～T8由于黄河充填层中夹层的存在，不同深度的含水率较CK2均在一定程度上得到了提高。

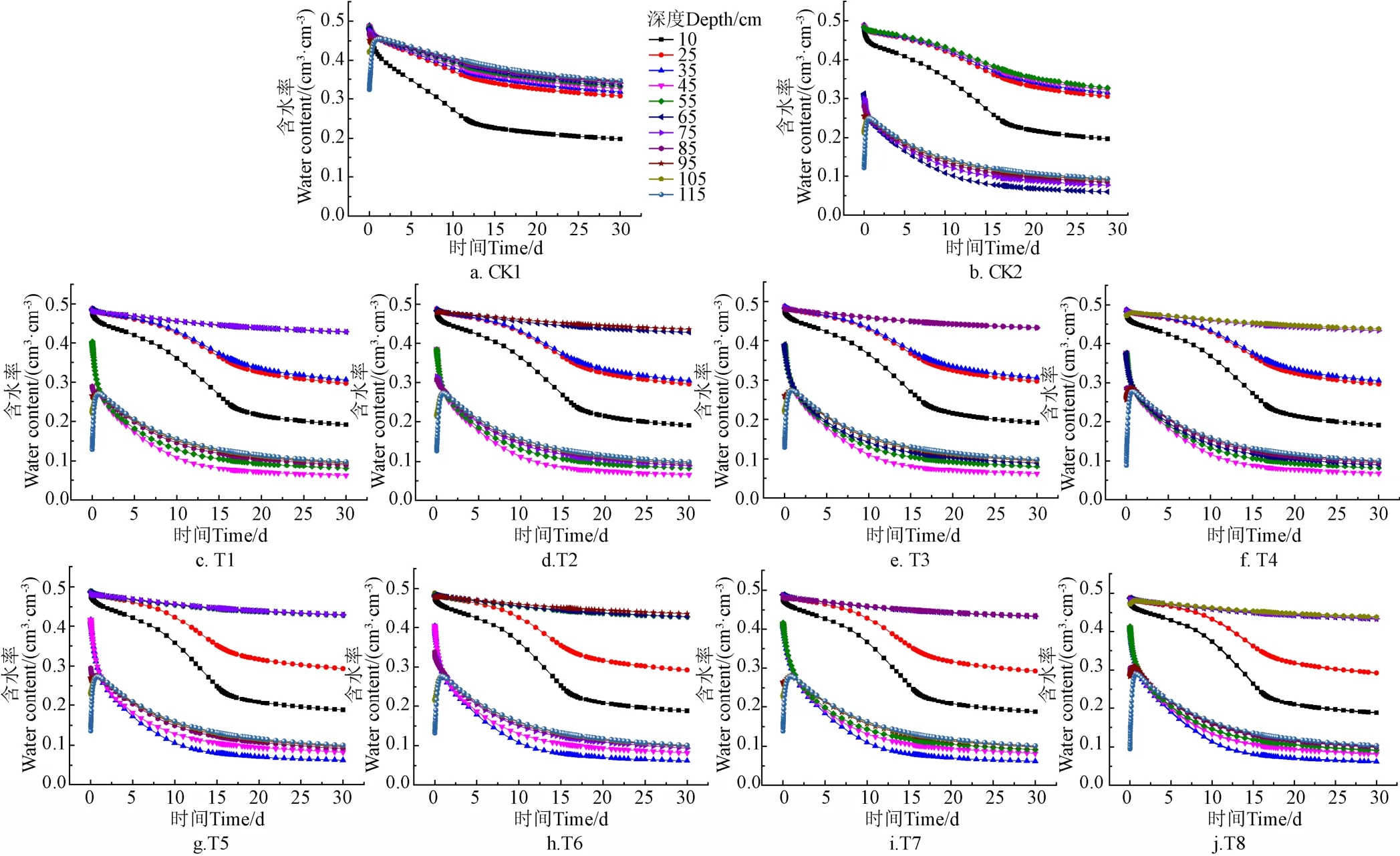
图9 蒸发阶段各处理不同深度剖面含水率随时间的变化 Fig.9 Change of water content in different depth profiles of each treatment at evaporation stage

2.4 正交分析夹层对持水能力的影响

本研究参考Xing等的研究，引入持水系数（Water Retention Coefficient，）综合入渗和蒸发两个过程黄河泥沙夹层式重构土壤的持水量，定量分析重构土壤的持水能力。为蒸发后的土壤持水量占入渗后的土壤持水量的百分比，其值越大土壤的保水能力越好，反之土壤的持水能力越差。根据入渗和蒸发试验设计，入渗结束时垂直剖面的土壤水分可以看作是蒸发的初始土壤水分。由表4可以看出，CK1的持水系数最大（=62.05%），而CK2的持水系数最小（=46.20%）仅为CK1的74.45%。CK2的持水性差，不利于复垦农田土壤水分的保持，在农业生产实践中，若与未损毁农田同样浇水量的情况下，“上土下沙”土壤剖面的复垦农田持水量可能仅为未损毁农田的一半左右，造成水资源的浪费。

表4 不同处理重构土壤的持水参数 Table 4 Water retention parameters of reconstructed soil with different treatments

黄河泥沙夹层式充填复垦提高了重构土壤的持水能力，T1～T8 的值分别为51.78%、52.50%、52.49%、55.11%、56.14%、56.05%和55.96%。当夹层位置为20 cm 时(T1、T2、T5、T6)的值较CK2分别提高了12.08%、13.63%、19.29%、21.51%，说明增加夹层厚度及夹层数量均能在一定程度上提高持水系数；当夹层位置为30 cm时（T3、T4、T7、T8）的值较CK2分别提高了13.62%、13.61%、21.32%和21.14%，说明增加夹层厚度能够提高持水系数，而增加分层数对持水系数的改变不大。

根据试验设计方案，模拟分析了夹层厚度、位置和数量不同水平组合下的土壤水分入渗和蒸发特性。不同处理夹层结构对黄河泥沙夹层式重构保水性的影响，可采用持水系数定量表示。以持水系数作为指标，正交试验结果分析表如表5所示。“1”和“2”分别代表各因素的两种不同水平，为极差，12为各因素不同水平的均值。对于交互作用的三列：A×B、A×C 和B×C 所在列的数字没有实际意义，但它们对于值的计算具有统计意义，可根据极差的大小，排出主次顺序。

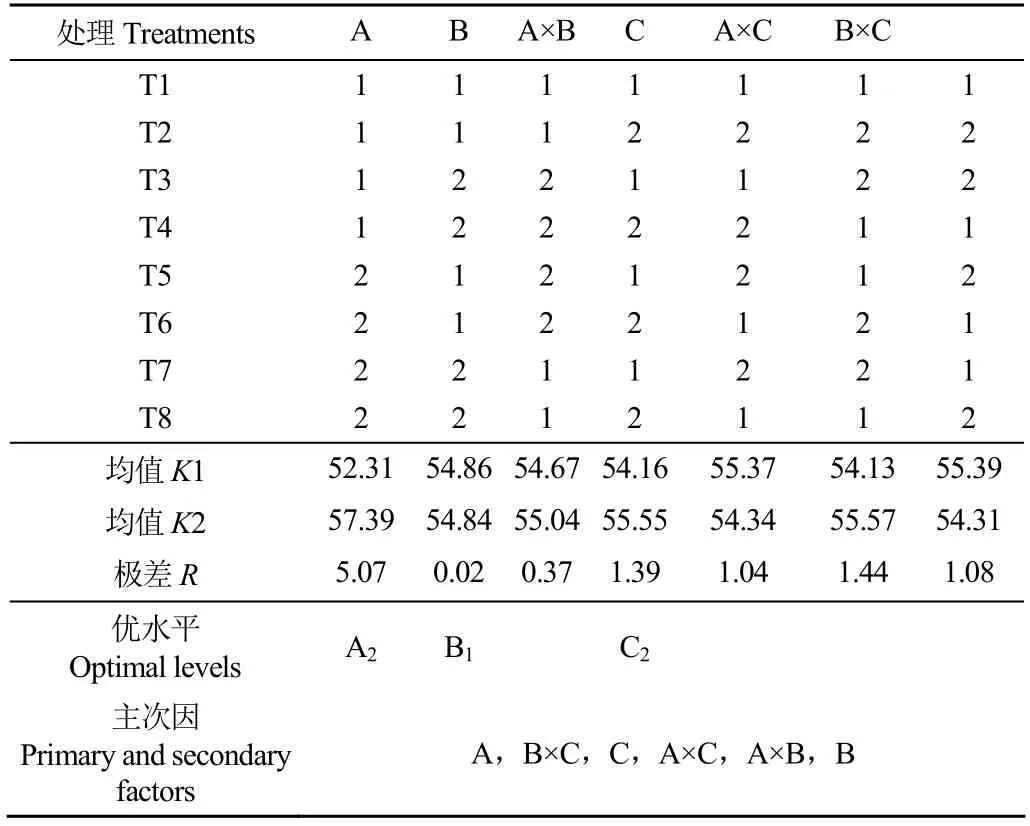
表5 正交试验结果 Table 5 Results of orthogonal test

根据主次因素的排序可得出，夹层厚度对持水系数的影响最大。而夹层位置与数量的交互作用，较夹层厚度与位置以和夹层厚度与数量的交互作用而言影响更大。由于B×C对试验指标的影响大于因素B、C对试验指标的影响，因素A和C是对试验指教具有较大影响的主要因素，所以可以直接用A和C的最优水平作为A×C 的优搭配，为AC。对于具有最大交互作用的B×C，不可直接根据单因素的单独作用确定最优水平，因此采用二元表进行计算分析如表6所示，考虑因素间的优搭配，最终确定最优搭配为BC。综合考虑A的优水平，可确定最优组合为ABC，即处理T6（夹层厚度为30 cm、夹层位置为20 cm、夹层数量为2层）剖面保水性要优于其他试验处理。

表6 B×C 二元表 Table 6 B×C binary table

3 结 论

本研究模拟分析了不同夹层厚度、数量和位置的改变对黄河泥沙充填复垦土壤水分入渗及蒸发特性的影响，研究结论如下：

1）黄河泥沙夹层式土壤剖面构型能够有效改善“上土下沙”土壤剖面构型的水分入渗特性，T1～T8由于黄河泥沙充填层中心土夹层的存在，形成了不同程度的水流障碍，有效提高了心土层上方黄河泥沙层的含水率。

2）黄河泥沙夹层式土壤剖面构型能够有效改善“上土下沙”土壤剖面构型的水分蒸发特性，随着夹层厚度的增加能够有效的抑制土壤水分的蒸发，而夹层的位置和厚度对累积蒸发量大小的改变关系不明显。在蒸发过程中表层土壤及黄河泥沙层中的水分先丢失，充填层中心土夹层在整个蒸发过程中都保持较高的含水率。

3）黄河泥沙夹层式土壤剖面构型能够有效改善“上土下沙”土壤剖面构型的保水性，持水系数较CK2可提高21.51%。分析表明夹层厚度为主要影响因素，夹层位置对持水系数的影响最小，夹层位置和夹层数量的组合具有最强的交互效应，最终确定处理T6（夹层厚度为30 cm、夹层位置为20 cm、夹层数量为2层）的夹层式土壤剖面的保水性最佳。

本研究为黄河泥沙夹层式土壤剖面优化设计，提出了一种经济时效的方法。这对探明黄河泥沙充填复垦土壤夹层结构的作用机理，并促进黄河泥沙夹层式充填复垦技术在黄河流域采煤塌陷地的推广应用具有重要意义。