基于最优分布拟合的拖拉机三点悬挂牵引力载荷谱编制与台架试验

王 玲，宗建华，王 禹，扶兰兰，毛 旭，王书茂

（中国农业大学工学院，北京 100083）

0 引 言

拖拉机三点悬挂装置是拖拉机关键零部件之一，各种不同类型农机具通过三点悬挂装置快速连接到拖拉机上，有效地提高了农田耕作效率。由于田间作业工况的复杂多变，拖拉机悬挂点承受较大的随机载荷，容易发生疲劳失效，直接影响拖拉机安全及作业效率。因此拖拉机三点悬挂装置作业载荷特性与分布研究对于预测零件寿命、产品可靠性分析等具有重要意义。

基于实测数据编制的载荷谱是疲劳寿命分析和可靠性试验的重要依据。目前，采用参数外推来预测不同工况下的全寿命载荷谱应用较为广泛。基于参数外推方法，贾海波等分别开展了轮式装载机传动系统、推土机车架纵梁、军用车辆传动系等零部件载荷谱测试及编制方法研究，翟友邦等以拖拉机动力输出轴及悬挂装置为研究对象，基于实测载荷数据进行了载荷谱与加速谱的编制。参数外推方法对单峰且分布均匀的载荷分布具有较好的拟合效果，对于多峰及概率分布不明确的载荷数据，传统参数外推编制方法中单分布难以实现载荷多峰分布的拟合问题，混合分布的研究更接近实际作业工况的载荷分布，基于此，翟新婷等基于混合分布函数采用双分布对测试载荷分布进行更精确的拟合，与单分布对比，双分布拟合效果更好；田维波等将EM（Expectation-Maximization）算法分别用于混合高斯分布和混合威布尔分布的数据拟合，编制装载机工作装置及数控刀架载荷谱。以上研究多基于载荷分布确定的工况开展研究，对于实际作业工况中载荷随机多变，单峰、多峰等分布难以确定的特征，上述研究无法实现各工况载荷分布的最优拟合，直接影响外推极值精度与载荷编制效果。

本文以拖拉机三点悬挂牵引力为研究对象，在传统参数外推基础上提出了一种基于最优分布拟合的载荷谱编制方法，通过建立混合分布模型并确定最优基函数个数，采用EM算法进行最优参数估计实现了极值频次外推与载荷谱编制。基于此，开发拖拉机三点悬挂牵引力室内台架加载系统，实现外推载荷谱的高精度模拟加载与复现，拟为拖拉机关键零部件载荷测试及疲劳预测试验提供理论依据和平台支撑。

1 拖拉机田间试验载荷采集

拖拉机三点悬挂牵引力田间试验在农业农村部南京自动化机械研究所白马基地开展，试验样机选用耕王RS-1254拖拉机配套1s-200深松机，在麦茬30 cm左右的麦田进行深松作业，试验作业平均速度约为4.2 km/h。利用拖拉机无线采集系统对三点悬挂牵引力载荷进行采集，田间试验及设备布置如图1所示。

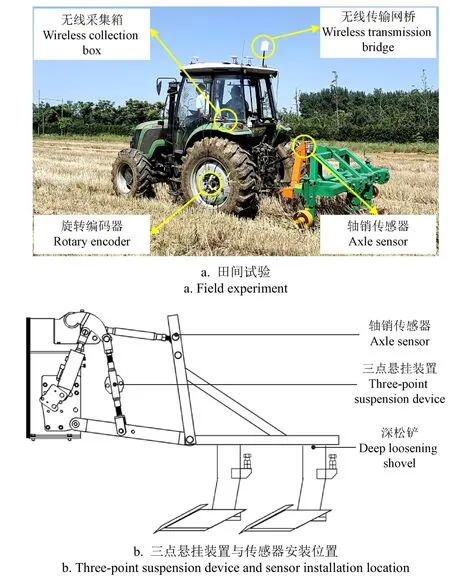
图1 田间试验及设备布置 Fig.1 Field experiment and equipment layout

拖拉机无线采集系统主要由轴销力传感器、数据采集箱、无线远程传输网桥及上位机监控软件等组成。由于拖拉机作业环境恶劣、田间基站网络信号差等问题，本文采用无线网桥实现数据采集箱与上位机监控软件的远程数据传输，稳定传输距离可达10 km；三点悬挂牵引力载荷频率为3～5 Hz，根据实际工程应用需求，采集频率应是载荷频率的3～4倍，因此数据采集箱采样频率为20 Hz。数据采集箱将数据无线传输至上位机监控软件，实现数据无线采集、显示与保存等。

由于作业环境复杂，采集的三点悬挂牵引力信号可能会存在异常数据，直接影响信号分析以及载荷谱的外推精度。为了获取三点悬挂牵引力载荷变化规律的真实信号，采用幅值门限、梯度门限、方差检测相结合的方法对载荷数据去除奇异点并进行滤波，并对处理前后数据进行统计特性分析，预处理后数据载荷历程如图2所示，预处理前后载荷极值没有变化，最大值和最小值分别为4.159 kN、0.259 kN，均值、标准差、方差分别降低0.4%、1.0%、1.7%。

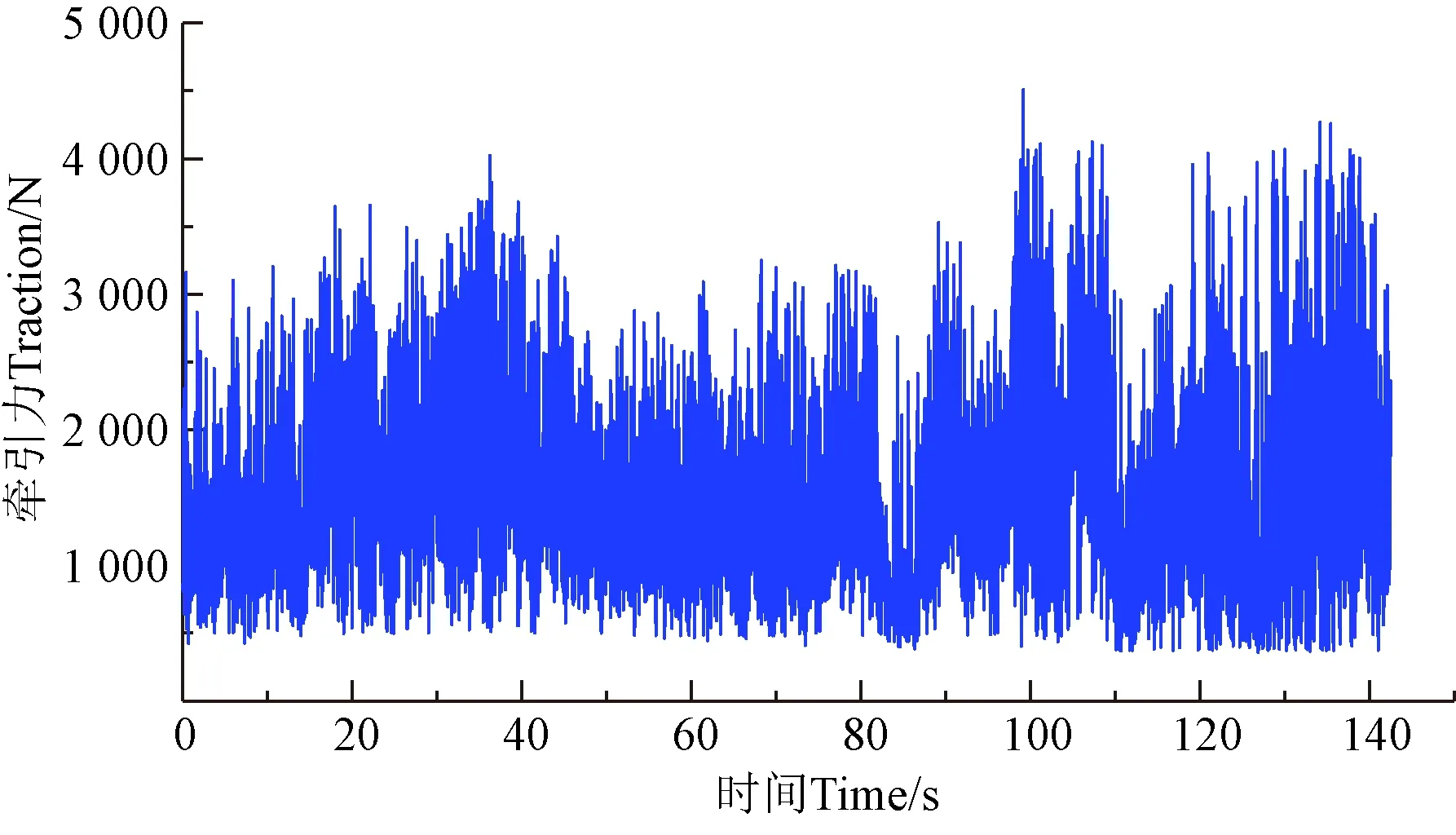
图2 预处理后三点悬挂牵引力载荷历程 Fig.2 Traction load course of three-point suspension after pretreatment

2 基于最优分布拟合的参数估计与验证

混合分布模型是指总体样本服从个来自不同分布特性的单样本分布函数，其分布模型表达式为

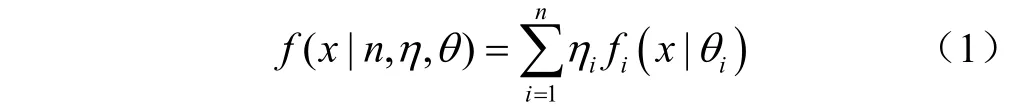
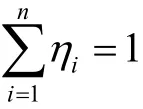
混合分布模型具有普适性，但在实际作业工况中载荷分布无法确定，因此很难使用混合分布模型进行分布拟合。在参数外推均值服从正态分布、幅值服从威布尔分布基础上，可以认为单峰分布或多峰分布的复杂载荷，其均值服从混合高斯分布，幅值服从混合威布尔分布，这样既可以降低计算复杂程度，也可很好地涵盖各工况分布特性载荷的拟合外推。

2.1 载荷统计计数与均幅值独立性检验

对于随机性较强的载荷，在进行载荷谱外推编制时，通常应用雨流计数法对测试载荷进行循环统计计数转换成雨流域载荷，本文采用四点雨流计数法对处理后载荷数据进行循环载荷频次统计，得到均值-幅值雨流矩阵以及均幅值频次图如图3所示。

图3 悬挂牵引力载荷雨流矩阵及均值幅值频次 Fig.3 Suspension traction rainflow matrix and mean amplitude frequency

为获得外推极值和频次，需要根据雨流矩阵以及均值、幅值频次数据，求出均值、幅值联合概率分布函数。若均值、幅值相互独立，其单独概率密度函数相乘即可得到联合概率密度。若均值、幅值不相互独立，则需要通过其他方法来确定其联合概率分布函数。

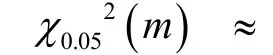
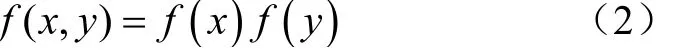
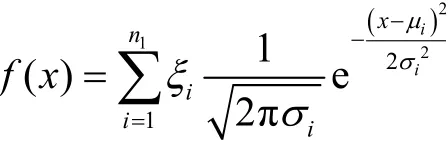
2.2 最优基函数个数确定

混合分布基函数个数即载荷分布是混合分布参数估计的前提和关键，且基函数个数直接影响混合分布的拟合效果，基函数个数过少会造成欠拟合，无法完整体现载荷数据分布，个数过多形成过拟合，部分数据不符合载荷分布。目前常用的基函数个数确定方法是将基函数从1开始递增，逐一进行混合分布参数估计，通过与原始数据拟合优度对比，得到最优基函数个数。通过总结，对于较为复杂的载荷分布，混合高斯分布和混合威布尔分布一般可以在基函数个数[1，10]和[1，5]之间找到最优解，若在初设区间内没有最优基函数个数，则区间进行倍数迭代扩大，直至找到极小值位置停止。由于实际作业工况下载荷样本数据无法直观呈现基函数个数，本文采用AIC准则（Akaike Information Criterion）与BIC准则（Bayesian Information Criterion）相结合的方法确定最优基函数个数。AIC准则通过综合模型拟合效果以及模型复杂程度来确定出基函数个数，对小样本约束性更强；BIC准则在AIC基础上引入后验概率检验，对大样本约束性更强，因此，AIC与BIC相结合的方法可先忽略样本容量，若AIC与BIC得到的基函数个数一致，则基函数最优个数确定，若不一致，则需要根据载荷样本容量进一步确定基函数个数。根据AIC和BIC求解公式如式（3）～（4），求取结果中最小值所对应的值即为最优基函数个数。

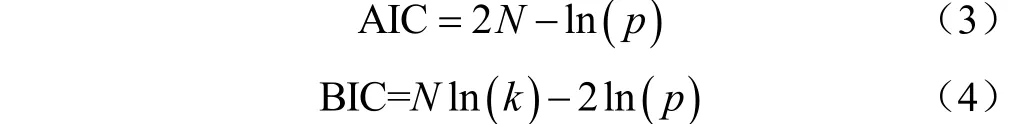
式中表示混合分布中基函数个数，表示混合分布极大对数似然函数值，为样本数量。

设混合高斯分布基函数最优个数取值[1，10]，混合威布尔分布基函数最优个数取值[1，5]，对式（3）～（4）计算得到混合分布基函数个数与AIC、BIC值的曲线图如图4所示。

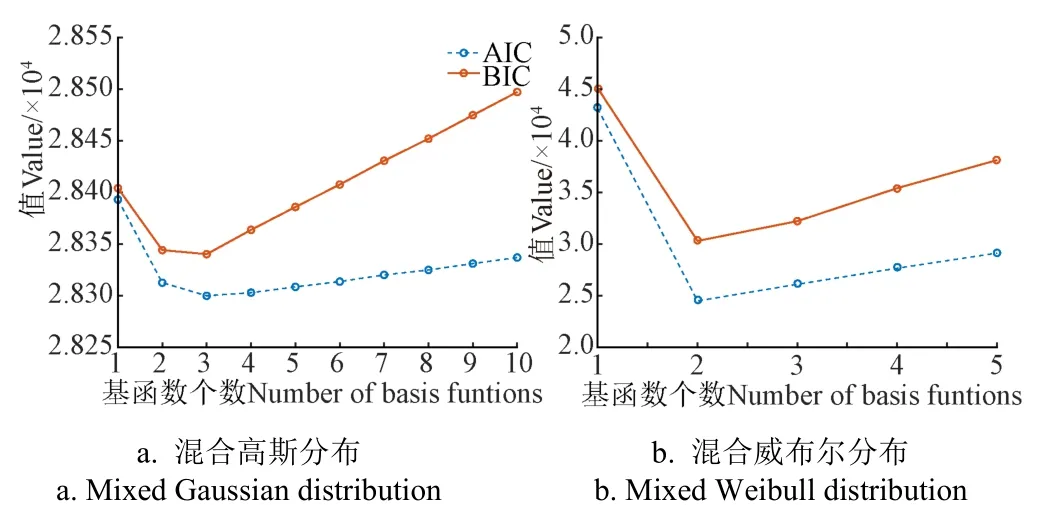
图4 基函数个数与基于AIC、BIC准则的值 Fig.4 Number of basis functions and the values based on the AIC（Akaike Information Criterion）,BIC（Bayesian Information Criterion）

由图4可知，当混合高斯分布基函数个数为3时，AIC与BIC值均最小，可认为均值服从基函数个数为3的混合高斯分布；当混合威布尔分布基函数个数为2时，AIC与BIC值均最小，可认为幅值服从基函数个数为2的混合威布尔分布。在实际的应用过程中，AIC准则与BIC准则得到最优基函数个数的值可能不同，此时需要根据样本容量的大小进一步确定基函数最优个数。

2.3 EM算法最优化参数估计

传统参数估计方法，必须在载荷数据比较完整的情况下，才能准确估计载荷分布参数。首先载荷根据基函数个数分成组，其次将分组后载荷进行参数估计，在参数估计过程中存在最优化分组以及部分数据未知无法直接得到分布参数等问题，因此，本文采用EM算法对载荷进行最优化分组与参数估计。以混合高斯分布最优化分组参数估计过程为例，过程分为E步和M步。首先，简化混合高斯模型，并求对数似然函数，进行E步，根据当前估计参数计算属于该类估计分布的后验概率，进行M步，求解估计参数，通过不断迭代计算，设第步迭代估计参数为 Θ，当参数 Θ使得对数似然函数最大时，即 ‖ Θ-Θ‖足够小时，参数 Θ为最优估计参数。

经过EM算法对混合分布见式（2）进行优化分组和参数估计，得到混合高斯分布与混合威布尔分布参数估计求解结果如表1所示。

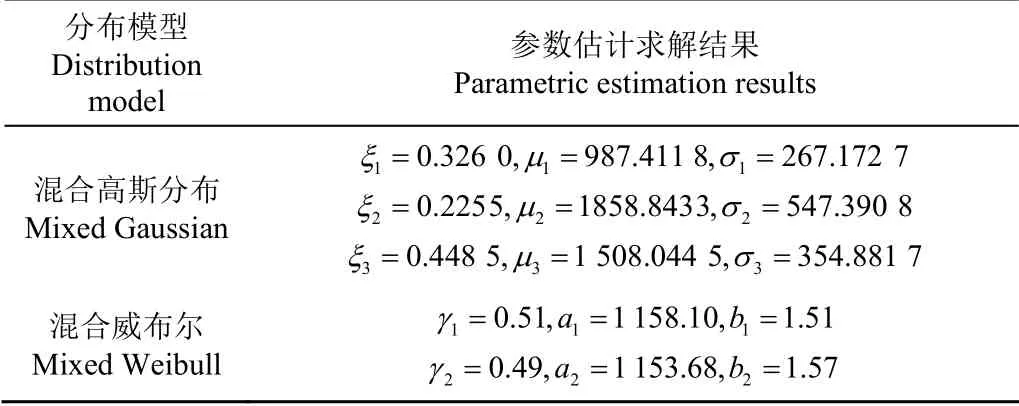
表1 混合分布参数估计求解结果 Table 1 Mixed distribution parameter estimation results

2.4 混合分布模型拟合效果检验

为验证拟合效果，分别从数据变化、误差、曲线拟合三个方面进行拟合效果检验。结果如表2及图5所示，从拟合效果检验参数看，单分布与混合分布拟合均通过检验，但是混合分布拟合效果明显提高。从数据变化角度，与单分布相比，混合高斯分布决定系数、相关系数分别提高3.45%和1.73%，混合威布尔决定系数、相关系数分别提高6.02%和4.87%；在误差角度，混合高斯分布均方根误差与残差平方和分别降低31.38%和52.92%，混合威布尔均方根误差与残差平方和分别降低40%和64.01%，检验结果表明混合分布更能准确描述载荷分布情况。

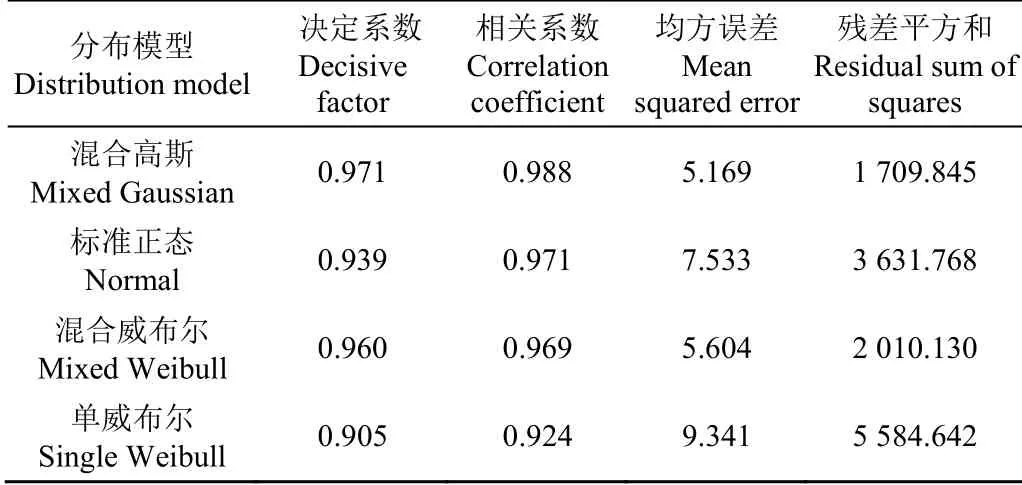
表2 混合高斯分布及混合威布尔分布拟合参数比较检验 Table 2 Mixed Gaussian and mixed Weibull fitting parameter comparison test

从概率密度拟合曲线比较图看，混合分布概率密度曲线走势基本与载荷数据一致，单分布在图5a、5c标注区域无法完全覆盖载荷频次信息，容易出现欠拟合；从累积分布函数（Cumulative Distribution Function，CDF）拟合曲线比较图看，可以认为混合分布CDF完全与实际CDF曲线吻合，而单分布与实际CDF曲线在图5b、5d标注区域有较大偏离，表明单分布在描述实测数据的载荷分布还有较大误差。

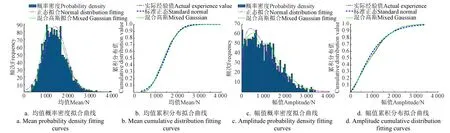
图5 混合分布与单分布拟合比较 Fig.5 Comparison of mixed distribution and single distribution fitting

3 程序载荷谱编制与台架动态加载试验验证

3.1 程序载荷谱编制及验证

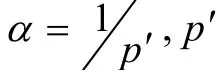
根据图3a的64级雨流矩阵联合概率密度函数可得到各外推倍数下每个均幅值区间的频次，目前八级载荷谱最为常用，均值、幅值均按照极值与比例系数（1、0.95、0.85、0.725、0.575、0.425、0.275、0.125）的乘积进行八级分级，并根据混合高斯与混合威布尔联合概率分布函数计算均幅值每个区间内对应出现的载荷频次，得到牵引力八级二维程序载荷谱如表3所示。

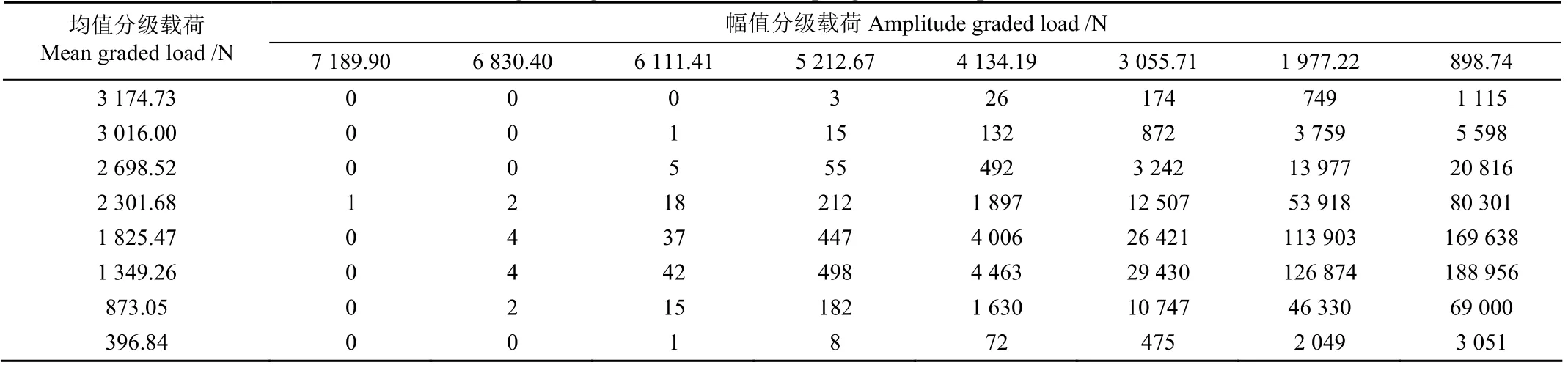
表3 牵引力八级二维程序载荷谱 Table 3 Eight-stage two-dimensional program load spectrum of traction

由于八级二维程序载荷谱难以用于加载系统进行加载，所以通常将二维载荷谱按照变均值法编制成一维程序载荷谱，求出均值波动中心，然后对波动中心进行施加相应级别载荷。波动中心为各分级载荷与频次乘积之和/总频次，得到波动中心为1 645.15N。基于Miner疲劳累积损伤理论以及S-N曲线，得到转换前后损伤累积公式如式（5）～（6），由转换前后疲劳损伤一致即=FD得到一维程序载荷谱的加载频次如表4所示，根据加载频次编制“低-高-低”的八级一维程序载荷谱，用于台架试验加载。

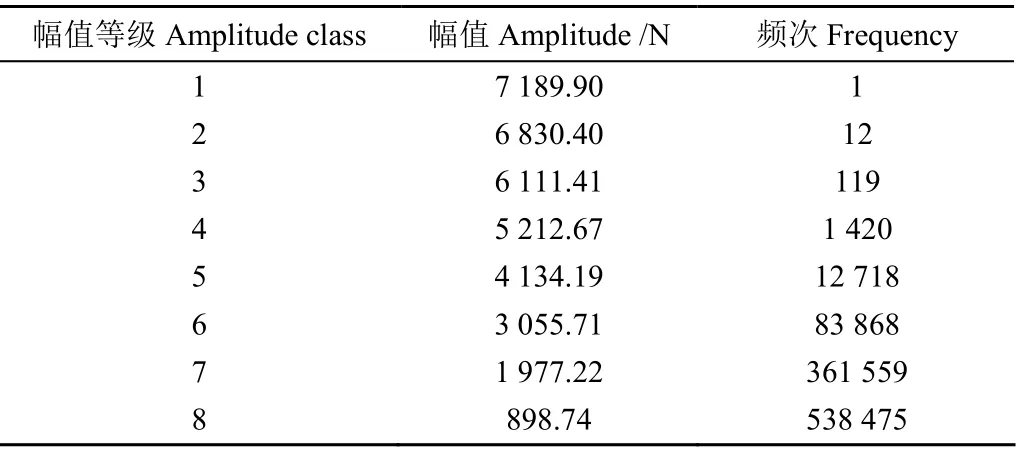
表4 牵引力八级一维程序载荷谱 Table 4 Eight-stage one-dimensional program load spectrum of traction

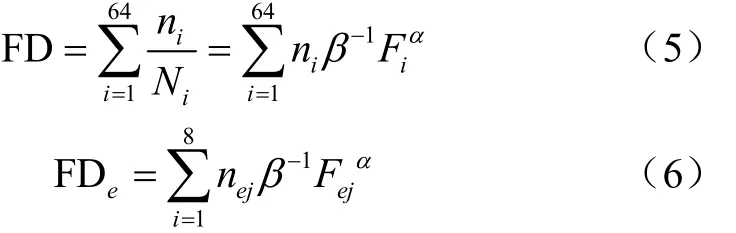
式中FD为二维程序载荷谱疲劳损伤；FD为一维程序载荷谱疲劳损伤；F为二维程序载荷谱分级幅值；n为的对应频次；N为应力下疲劳寿命的总频次；F为一维程序载荷谱分级目标幅值；n为的对应频次；为材料性质常数；为95%可靠度下材料对应的常数。

为更好分析外推前后的载荷数据统计特性以及均幅值频次信息，外推前后数据统计特性如表5所示，外推一倍载荷与原始载荷均幅值频次图如图6所示。从表5可以看出极值范围变大，扩大为原来的1.194倍，均值提高，但标准差和方差基本不变；从载荷频次图来看，外推一倍载荷谱与原始载荷均值幅值频次基本保持一致，均值频次整体向右偏移对应频次一致，幅值频次范围没有变化，说明外推载荷整体变大，而波动情况基本没有发生变化。

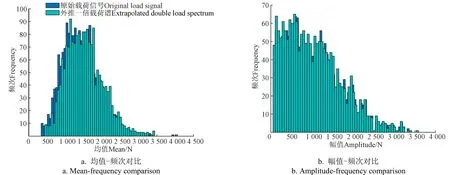
图6 外推一倍载荷谱与原始载荷频次对比 Fig.6 Comparison of extrapolated double load spectrum and original load frequency

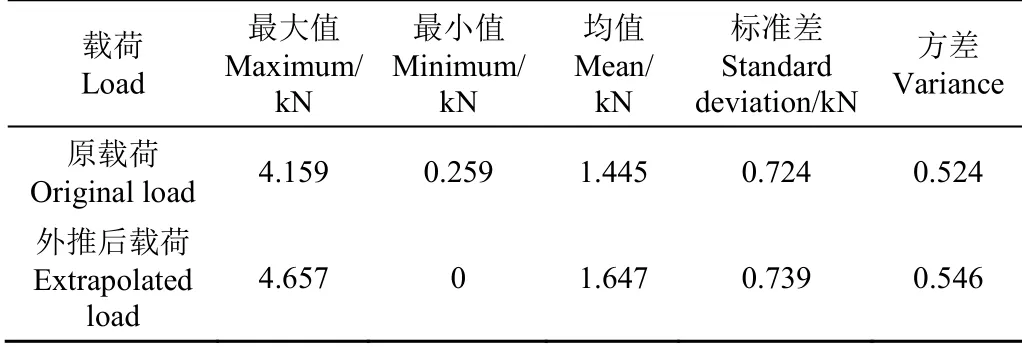
表5 外推前后载荷统计特性 Table5 Statistical characteristics of data before and after extrapolation

3.2 基于PID的拖拉机三点悬挂外推载荷谱台架试验验证

如图7所示，拖拉机三点悬挂牵引力室内台架加载系统由加载油缸、悬挂提升框架、牵引力传感器、拉绳传感器、角度传感器、电液比例溢流阀、比例换向阀及液压泵站等组成，设备参数如表6所示。拖拉机三点悬挂提升框架通过牵引力传感器与加载油缸相连，角度传感器安装在加载油缸支架底部；加载油缸对提升框架施加阻力，用于模拟拖拉机田间作业承受的悬挂载荷，并通过牵引力传感器与角度传感器检测模拟载荷大小及加载角度。加载力、加载方向及伸缩速度通过液压泵站、电液比例溢流阀及电液比例换向阀进行控制。此外，基于NI FPGA设计开发了拖拉机三点悬挂加载平台测控仪，用于传感器信号的实时采集与输出控制，实现数据的显示、保存及预处理等。

图7 拖拉机三点悬挂牵引力加载系统总体方案与实物图 Fig.7 Overall scheme and diagram of tractor three-point suspension traction loading system

表6 加载系统设备参数 Table 6 Device parameters of loading system

三点悬挂牵引力试验中，为简化控制系统的复杂性，保持系统压力与流量稳定，通过调节电液比例溢流阀回路压力，实现对加载油缸加载力的控制。试验中，将牵引力外推载荷谱作为目标信号用于加载系统，牵引力传感器实时采集加载力，基于PID反馈调节实现牵引力载荷谱的动态加载与复现。

由于加载设备动态响应性能有限，目前机械零部件疲劳寿命试验方法通常采用静态载荷加载或静态逐级加载的方式，无法真实还原田间作业载荷特征，影响机械零部件产品设计及疲劳寿命预测精度等。本文将外推一倍载荷谱用于加载试验，加载频率为20 Hz。牵引力载荷谱的加载效果如图8所示。

通过对实测牵引力和外推载荷谱输入牵引力曲线进行分析，两者均方差为280 N，系统最大超调量为5.19%，最大稳定时间为0.2 s，最大延时为0.4 s，系统动态响应效果较好；从图8可知加载系统存在0～450 N范围的加载死区，由于控制系统加载时，电液比例换向阀方向和开口大小确定，部分液压油经过换向阀进入油缸所致。通过学者的研究发现，删除最大载荷的10%～15%不会对零件的疲劳寿命产生明显影响，外推数据的最大值为4.657 kN，删除最大值的10%以下小载荷后，外推数据最小值为465.7 N，大于死区的范围，因此，可以认为加载死区对外推载荷谱加载影响可以忽略。从放大曲线可以看出，牵引力基本可以实时跟随载荷谱输入，室内台架系统能够满足拖拉机三点悬挂牵引力的动态加载和复现。

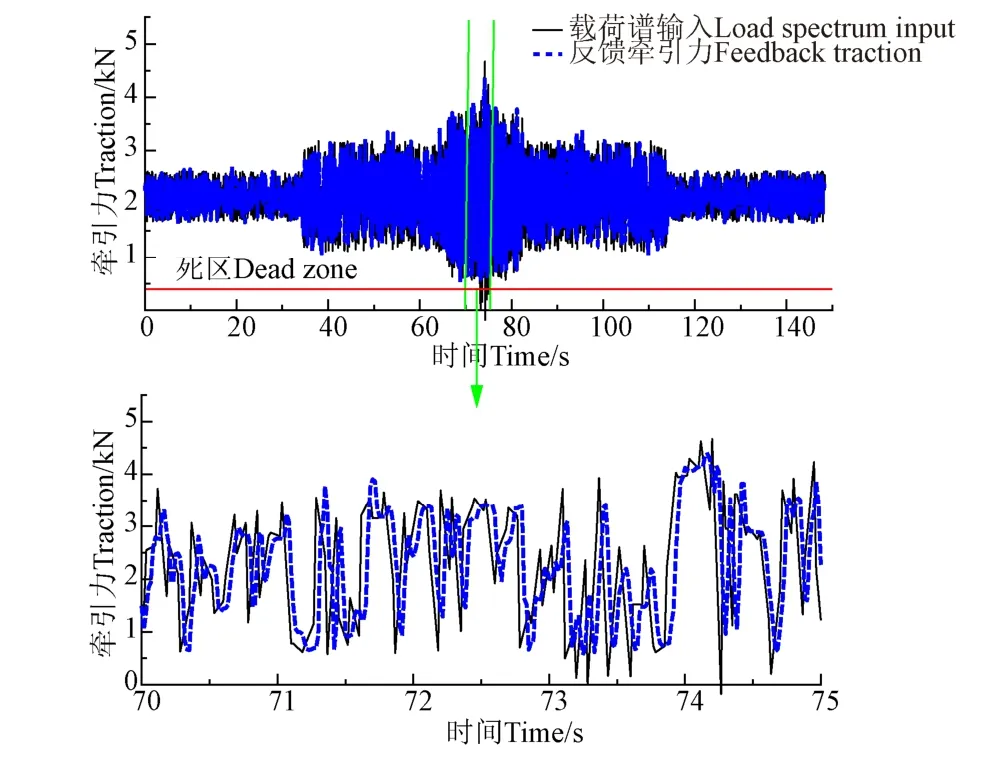
图8 牵引加载力与反馈力跟随曲线 Fig.8 Loading force and feedback force curves under different loading frequency

由Miner疲劳累积损伤理论以及S-N曲线可知，经过雨流计数之后，不同应力的次数与此应力下疲劳寿命的比值和代表该段应力数据的总寿命。对外推载荷、加载载荷进行雨流计数分析，得到均值、幅值频次对比如图9所示，可以看出外推一倍载荷与加载反馈载荷谱均值频次、幅值频次基本一致，可认为原始载荷、外推载荷、加载载荷造成的损伤等效，为基于载荷谱编制的拖拉机室内台架试验提供理论依据和参考。

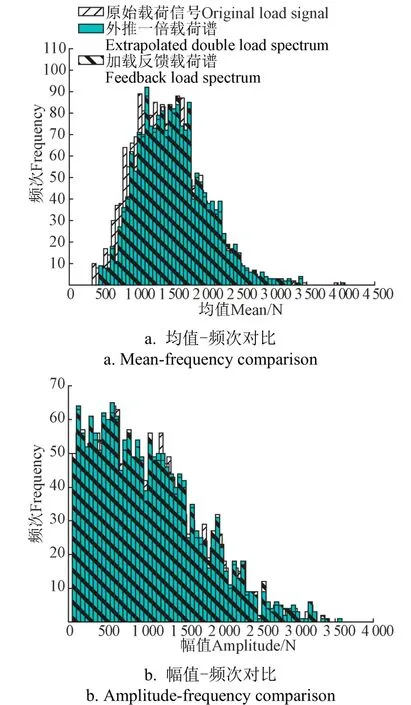
图9 外推载荷谱与加载载荷谱频次对比 Fig.9 Frequency comparison between extrapolated load spectrum and loaded load spectrum

4 结 论

1）以拖拉机三点悬挂牵引力载荷为例，建立混合分布模型，采用AIC准则与BIC准则相结合的方法确定混合分布最优基函数个数，并基于EM算法进行最优分布拟合求解，通过与传统参数外推单分布拟合相比，混合高斯分布与混合威布尔决定系数分别提高3.45%和6.02%，相关系数分别提高1.73%和4.87%；均方根误差分别降低31.38%和40%，残差平方和分别降低52.92%和64.01%，验证结果表明该方法的拟合效果总体更能准确描述载荷分布情况。

2）提出了基于最优分布拟合的载荷谱编制方法，将原始载荷极值和频次外推至10编制一维程序载荷谱，并将外推一倍载荷谱与原始载荷数据进行对比分析：外推后载荷范围扩大为原来的1.194倍，标准差和方差基本保持不变；雨流计数后均值频次整体向右偏移但对应频次一致，幅值频次范围没有变化，说明外推载荷极值范围得到扩充，疲劳损伤进一步扩大，能够在保留原始载荷规律特性的前提下实现均幅值的双向外推。

3）开发了一套拖拉机三点悬挂牵引力室内台架加载系统，并基于PID控制实现悬挂牵引力的反馈调节。将基于上述方法的外推牵引力载荷谱数据与实测牵引力数据进行对比分析，结果表明：加载系统最大超调量为5.19%，最大稳定时间为0.2 s，最大延时为0.4 s，室内台架系统能够满足拖拉机三点悬挂牵引力的加载与复现，并对加载载荷谱与反馈载荷谱进行雨流计数分析，均值、幅值频次一致，两者疲劳损伤等效，为基于载荷谱编制的拖拉机室内台架试验提供理论依据和参考。