基于浸入边界法的翼型俯仰振摆动态特性

2022-04-19李昊宇徐宇航

农业工程学报 2022年2期

阚阚，李昊宇，吕品，徐宇航，郑源，徐辉

（1. 河海大学能源与电气学院，南京 211100；2. 河海大学水利水电学院，南京 210098；3. 中国船舶集团有限公司第七一〇研究所，宜昌 056002；4. 河海大学农业科学与工程学院，南京 211100）

0 引言

翼型俯仰振摆会引起流场显著的非线性变化，在气动弹性和非定常流体动力学领域受到越来越多的重视，被认为是喷气发动机、风力发电机和水力机械等动力设备设计中的关键问题之一。在工程中翼型的振摆通常分为受迫振摆和主动振摆两种情况。其一，风力机、水轮机等流体机械在运行中，由于结构约束不足或者变桨叶调节机构失灵，叶片可能发生一定程度的振摆，从而导致流体机械的动态性能发生剧烈波动，甚至造成流体机械的破坏。其二，主动振摆的襟翼可以用来调节风力机、飞行器以及水下航行器等设备动态性能，是近年来研究的工程热点。因此对翼型俯仰振摆动态特性的研究具有极高的理论价值和实际工程意义。

针对翼型作俯仰振摆运动的动态特性，国内外学者主要围绕振摆频率、振摆幅值、振摆平均攻角及俯仰轴位置等参数展开了研究。Amiralaei等对低雷诺数下翼型俯仰振摆的研究指出振摆频率和振摆幅值对动力学性能有着重要的影响。Tian等发现随着翼型俯仰轴位置的前移，翼型产生的推力增加。薛臣等指出振动轴位置主要改变翼型的有效迎角，而振摆频率的增大会导致翼型周围流场结构产生变化。李晓华等通过数值模拟对俯仰振摆减缩频率和平均攻角的研究表明减缩频率对翼型气动特性的影响主要在翼型攻角的下行段。Kurtulus发现在小幅值的振摆中，振摆频率会对升力波动幅值产生影响。而对于上述参数对翼型俯仰振摆动态特性的影响机理，前人也进行了许多研究。Worasinchai等利用风洞实验方法研究了垂直轴风力机叶片翼型在高频振摆运动中的表面非稳态的压力变化，研究指出了翼型的振摆运动导致的前缘涡的形成与脱落对于翼型表面的压力分布有显著影响。李绍斌等通过数值模拟研究了平均攻角和振幅对俯仰振荡翼型气动特性的影响，指出翼型振摆过程中上仰阶段前缘涡的产生和集中涡的稳定附着是平均升力系数随振幅增大呈阶跃式提升的原因。

虽然对于翼型俯仰振摆动态特性已经开展了很多研究，但目前关于翼型在俯仰振摆运动过程中升力系数发生的波动与流场中旋涡发展演化的相关性方面的研究仍然不够深入。此外，前人对俯仰振摆翼型的研究所采用的数值方法大多基于贴体网格，其在处理快速移动边界时存在一定的局限性，可能因为网格拉伸过大、网格质量下降等原因影响模拟结果的精确性。而浸入边界法（Immersed Boundary Method，IBM），是处理此类动边界问题的一种有效方法，由Peskin于1972年首次提出。相比传统的基于贴体网格的数值方法，因其无需生成贴体网格和进行网格移动与重生，从而具有较高的计算效率，可以相对高效地处理具有移动边界的流动。王文全等通过自编程序验证了浸入边界法可用于模拟流体刚体的耦合运动，但是采用浸入边界法对作俯仰振摆运动的翼型的动态特性进行的研究还较少。

因此本文采用基于浸入边界法的自编求解器，对雷诺数=1000条件下NACA0012翼型以弦长1/2处为中心作不同初始攻角、不同振摆频率、不同振摆幅值的俯仰振摆运动进行二维流动直接数值模拟（Direct Numerical Simulation，DNS），分析各工况下升力系数的波动特性和升力系数波动与流场演变的相关性，同时验证浸入边界法对瞬态流动捕捉的准确性。研究结果拟为工程中风力机等流体机械翼型颤振引起的流动不稳定性研究提供理论参考和工程依据。

1 数值方法及验证

1.1 控制方程

不可压缩流体不考虑密度的变化，质量守恒方程（连续性方程）为

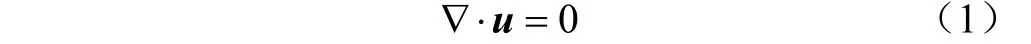
动量守恒方程（Navier-Stokes方程，N-S方程）为

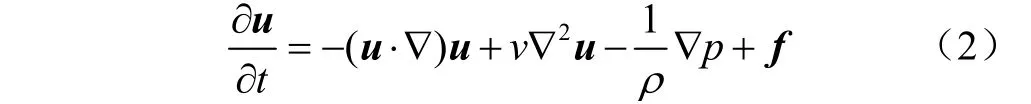
式中为速度，m/s；为流体密度，kg/m；为流体运动黏度，m/s；为压力，Pa；为对浸入边界（Immersed Boundary，IB）点施加的外部源项体积力，m/s。

1.2 空间离散

采用直角坐标系下的笛卡尔交错网格，基于二阶中心差分格式的有限差分法进行离散。、、分别为速度在轴方向的正交分量，定义在网格单元体面心；而其余物理量例如密度、压力等定义在网格体心，如图1所示。

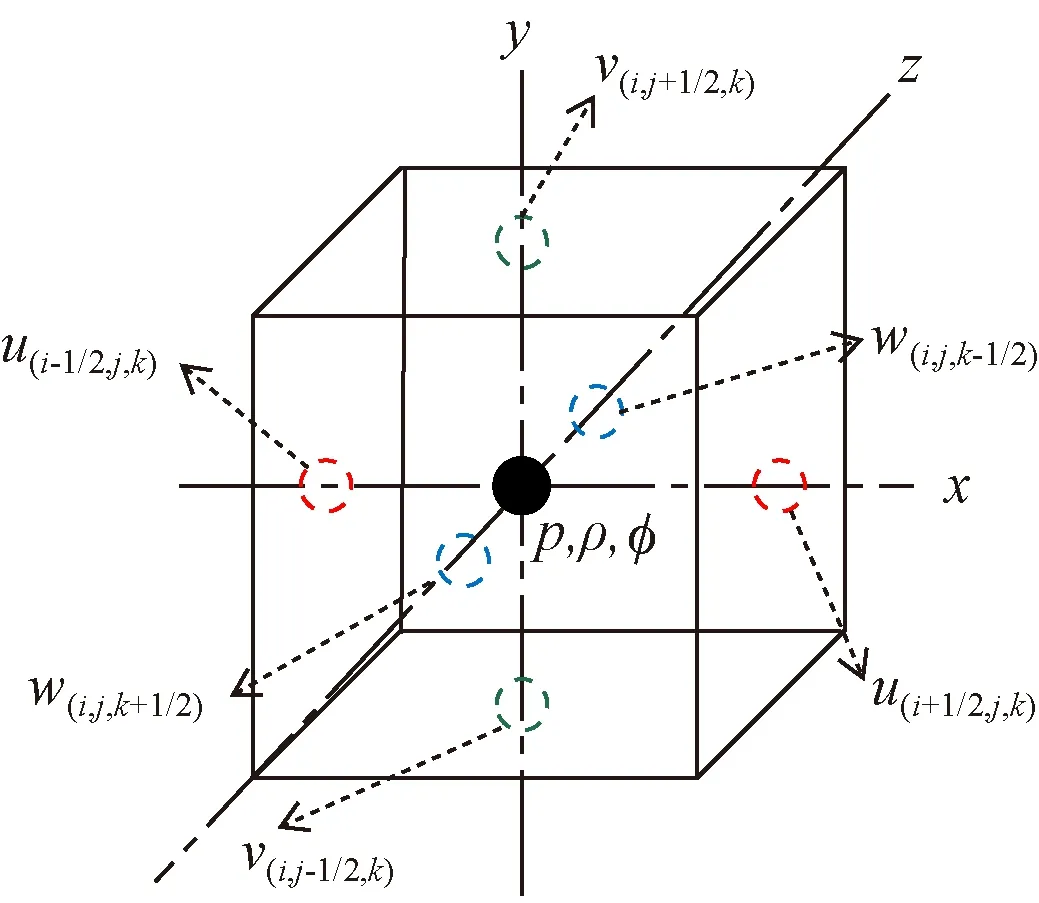
图1 空间离散网格示意图 Fig.1 Schematic diagram of spatial discrete grid

1.3 时间步推进与压力泊松方程求解

采用投影法与二阶龙格-库塔法（Runge-Kutta Method，RKM）推进计算时间步。二阶龙格-库塔法将求解分为两个时间子步进行迭代求解，在每一时间子步中利用投影法分步计算N-S方程各项对速度场的影响并叠加推进计算进行，同时保证无散度条件。以第一步龙格-库塔法为例进行说明（下文说明均以第一步龙格-库塔法为例），其过程如公式（3）至（6）所示。

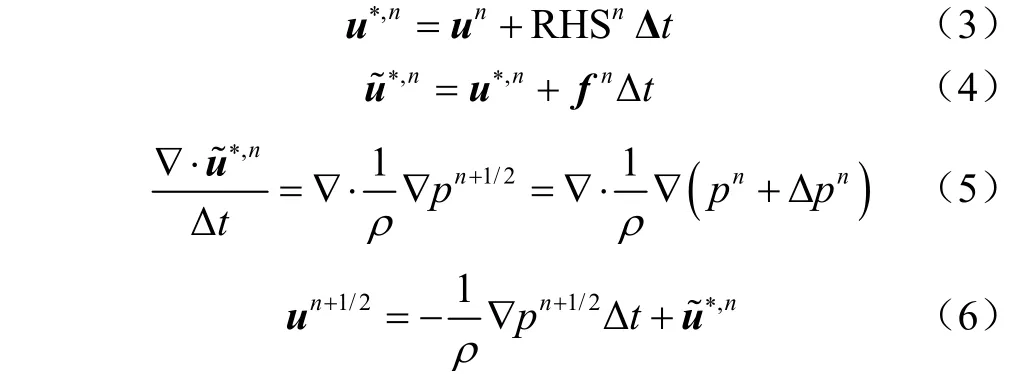
式中各物理项的上标为时间子步序号。u为计算第步的速度场，u为龙格库塔法的中间速度，Δ为求解时间步长。N-S方程右侧的粘性项∇与对流项-(∙∇)之和记为RHS（Right Hand Side）。u表示时间子部中忽略固体存在性的速度场。对IB点进行速度插值并通过公式（4）得到更新后的速度场~。求解压力泊松方程时采用的求解器为 PETSc（Portable，ExtensibleToolkit for Scientific Computation），即科学计算可移植扩展工具包，可以对偏微分方程组高效并行求解。为减少泊松方程迭代次数，根据公式（5），泊松方程求解结果为各时间子步计算前后的压力差Δ，即相对压力。将求解泊松方程得到的相对压力Δp与p相加获得+1/2时刻无量纲绝对压力p，若求解节点为流体点则忽略体积力

1.4 基于水平集函数的浸入边界法

为使流固交界处流体速度满足无滑移边界条件，在IB点施加一个外部源项的体积力，在求解N-S方程时需得到此力对流场的影响以更新速度场。

采用Sussman等的水平集方法（Level-Set）用于翼型界面的追踪，将NACA0012翼型边界定义为零水平集，见公式（7）。

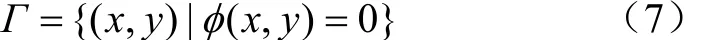
首先需确定各节点的水平集函数值，将各速度分量所在节点分类为固体点、流体点与浸入边界点。特别地，因使用交错网格，速度分量定义在网格面心，而水平集函数定义在网格体心，故在定义速度节点类型时需要通过相邻的两个网格的水平集函数值通过线性插值的方法得到网格体面的水平集函数值。水平集函数值定义如公式（8）所示。

式中为此节点沿水平集函数梯度方向相对固液边界的坐标。若一节点<0，则将其定义为固体点。在二维情况中，若一节点>0，且其4个相邻节点均满足>0，则将其定义为流体点，若一节点>0，且其4个相邻中存在满足<0的节点，则将其定义为IB点，见图2。

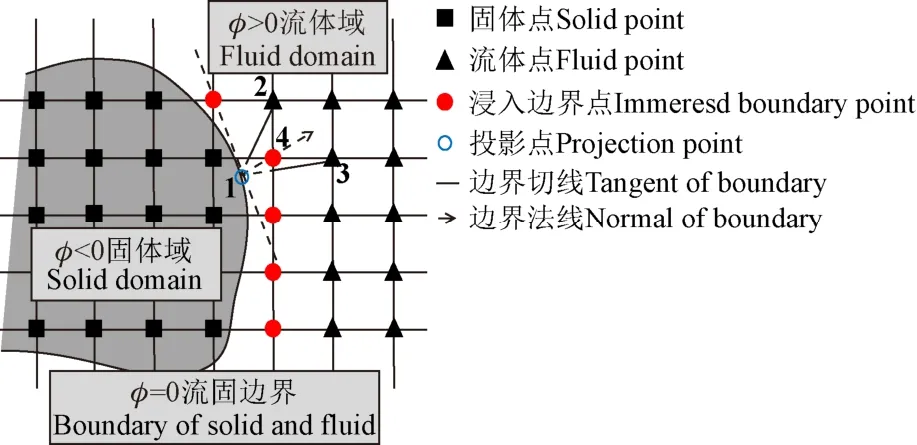
图2 浸入边界法示意图 Fig.2 Schematic diagram of immersed boundary method

以IB点4的计算为例，利用流固耦合边界两侧节点水平集函数值求梯度，得到IB点4沿梯度向量在流固边界上的投影点1，点2、3为对点4进行速度插值的模板点。记IB点4在整个计算域的坐标为(,)，结合水平集函数梯度以及网格长度可计算得到点1、2、3的坐标，分别为(,)、(,)、(,)。点1速度由固体本身的运动状态决定，记为，点2、3速度分别记为、。通过求解线性方程组（9）得到插值系数、、，根据公式（10）对IB点速度基于无滑移边界条件线性插值更新速度场。

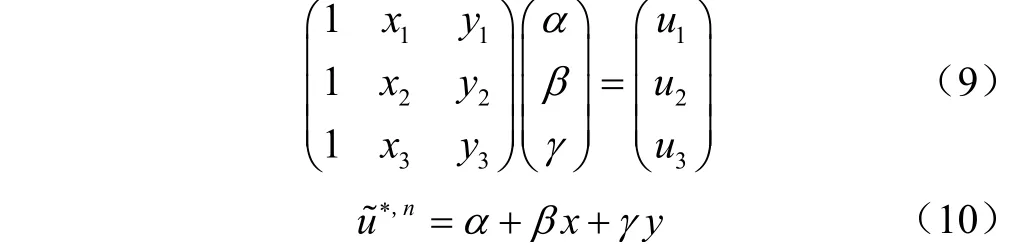
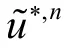
2 计算设置与方法验证

2.1 计算设置

采用1 024×768×3的笛卡尔坐标系下的交错网格，对NACA0012进行二维流动直接数值模拟。取典型低雷诺数流场，雷诺数如公式（11）计算所得。

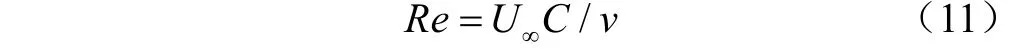
式中U为来流速度，0.146 m/s；为特征长度，此处即为翼型弦长，0.01 m；为流体的运动黏度，此处取值1.46×10m/s，即雷诺数=1 000。为确保翼型振摆过程中的尾流场捕捉的准确性，同时减少计算域边界对翼型周围流场的影响，计算域中方向的长度为10，方向的长度为7。翼型周围采用加密网格计算，加密中心为(4,3.5)，方向加密长度为4，方向加密长度为3。计算域进口为正方向的均匀入流，计算域右侧出口边界条件为对流出口，上下边界均为自由滑移边界条件。计算域示意图见图3。

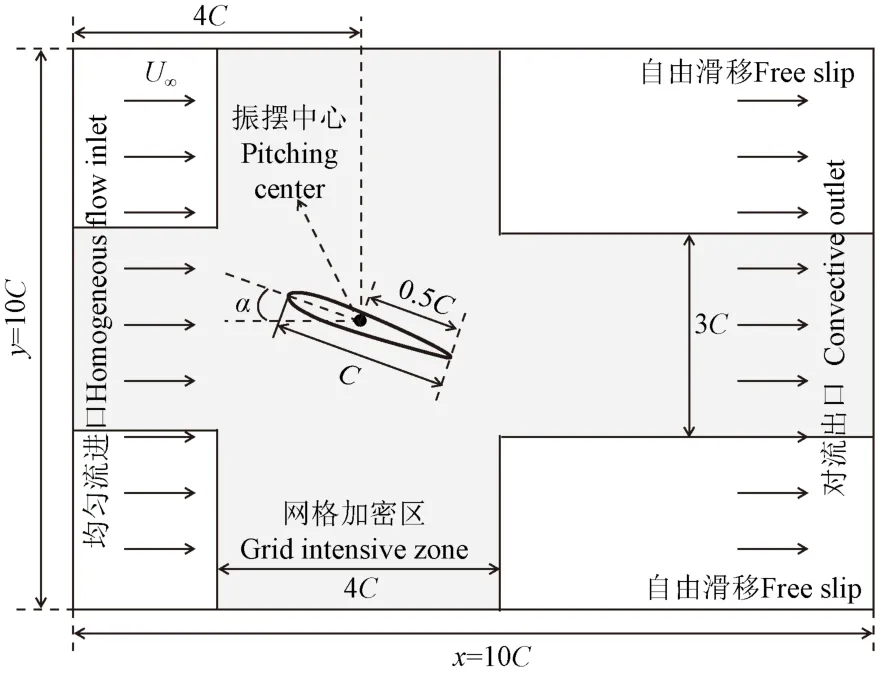
图3 计算域示意图 Fig.3 Schematic diagram of computing domain

翼型振摆中心位于弦长1/2处，攻角为，振摆由公式（12）控制，其角速度见公式（13）。

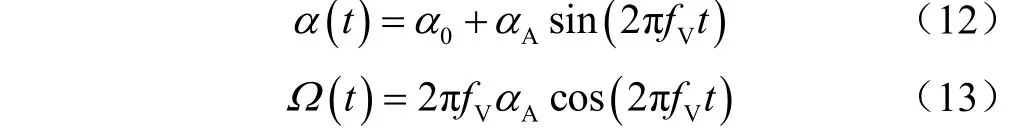
式中为初始攻角，(°)；为最大振摆幅度，(°)；为振摆频率，Hz；为时间，s。

2.2 方法验证

本次研究首先通过对不同攻角下的NACA0012静止翼型的升力系数、阻力系数、斯特劳哈尔数进行计算并与已有文献对比，以验证计算数值方法、计算网格的准确性及可靠性。为进行验证对比，结合翼型较为常见的运行工况，分别选取静止状态下攻角分别为=5°、10°、15°、20°的情况进行流动模拟。升力系数、阻力系数及斯特劳哈尔数的定义见公式（14）～（16）。

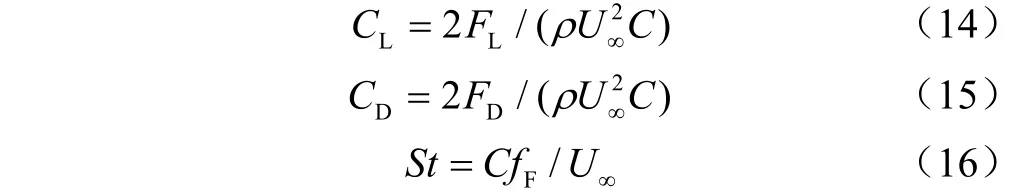
式中F、分别为翼型受到的升力和阻力；为翼型尾部涡脱落频率。本文采用的求解器计算过程中各物理量均为无量纲，速度，长度，时间的无量纲化过程见公式（17）。

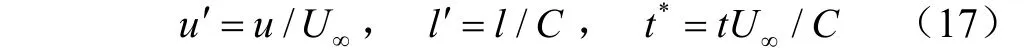
式中为无量纲化后的速度；为无量纲化后的长度；为无量纲化后的时间，同时无量纲压力p与无量纲涡量定义如下：

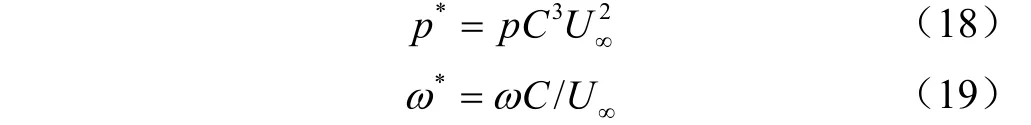
式中为涡量，1/s。

本次计算结果与其他文献中数值模拟的结果对比见表1，此处升力系数、阻力系数为时间平均系数。由表可见，本次计算结果均与各文献结果吻合良好。

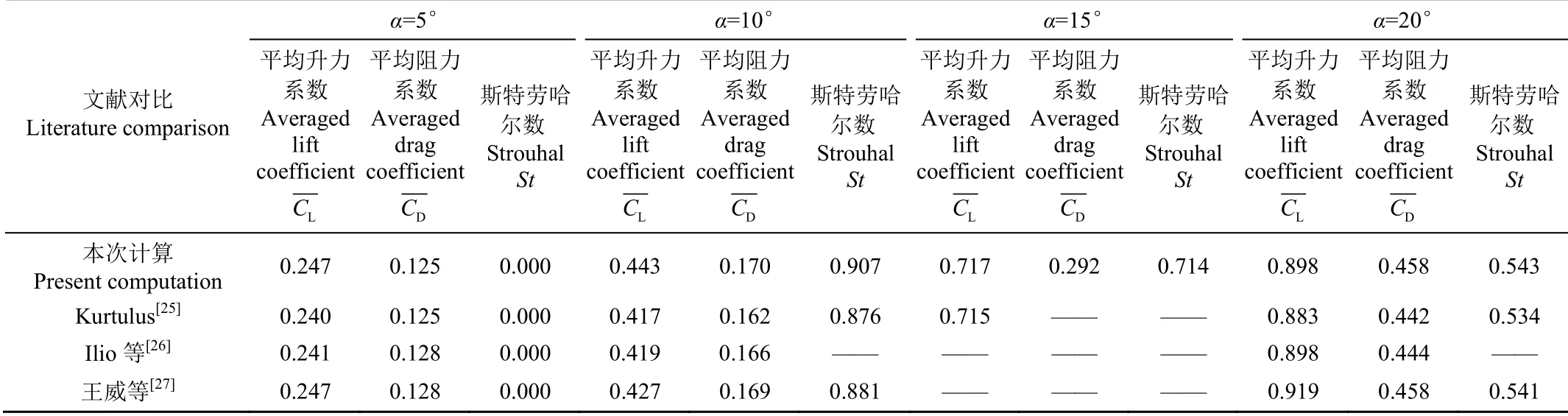
表1 不同攻角平均升力系数、阻力系数、斯特劳哈尔数对比 Table 1 Comparison of averaged lift coefficient, drag coefficient and Strouhal number at different attack angles (α)

同时，为进一步验证求解器对流场信息捕捉的准确性，选取=5°、=10°、=15°的涡量（无量纲）瞬时分布图（图4），升力系数随时间变化图（图5a）和频谱图（图5b）进行观察分析。由图可见，5°攻角时，吸力面与压力面边界层稳定，均未发生流动分离，翼型尾部流迹稳定，无脱落涡产生，计算收敛后流动稳定且升力系数不发生波动。10°攻角时，吸力面产生了明显的流动分离，分离点由后缘前移并产生了周期性旋涡脱落，压力场随旋涡脱落发生变化使得升力系数曲线产生波动，由升力系数频谱可得旋涡脱落频率为13.255 Hz。在翼型攻角增加至15°时，吸力面流动分离点继续向前缘移动，脱落涡尺度和强度增大，涡形成位置更加靠近尾缘，翼型压力面边界层形成明显的逆压梯度流动，频谱图中出现频率为主频10.309 Hz及其倍数的次频。通过与已有文献数值模拟结果升力系数、斯特劳哈尔数等参数以及涡量分布的对比结果表明本求解器可以准确捕捉翼型周围流体流动过程中的升力波动与旋涡的产生。

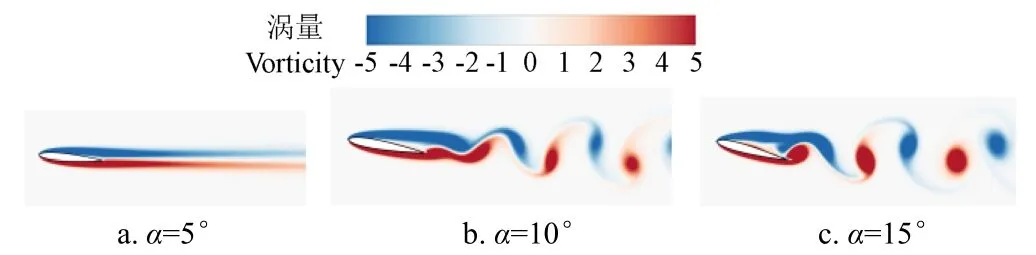
图4 静止状态不同攻角下瞬时涡量云图 Fig.4 Instantaneous vorticity nephogram at different attack angles at static condition

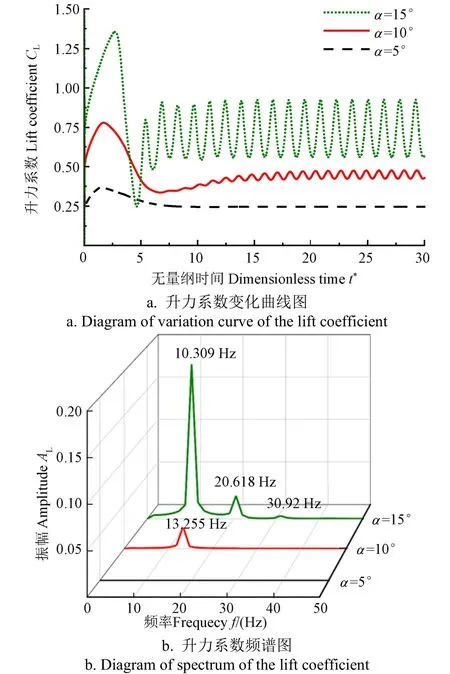
图5 不同攻角静止状态升力系数变化曲线图及升力系数频谱图 Fig.5 Diagram of variation curve and spectrum of the lift coefficient at different attack angles at static condition

3 试验与结果

3.1 翼型振摆下的升力系数时频特性

翼型振摆主要将初始攻角、振摆频率、振摆幅值这三个主要因素作为变量进行考虑。根据翼型在实际工程的主要运行工况和相关文献，初始攻角选择=5°（小攻角）、=10°（中攻角）、=15°（大攻角），振摆频率选择1.46 Hz（低频）、2.92 Hz（高频），振摆幅值选择=5°（小幅值）、=10°（大幅值）。各工况翼型振摆运动参数及平均升力系数见表2。

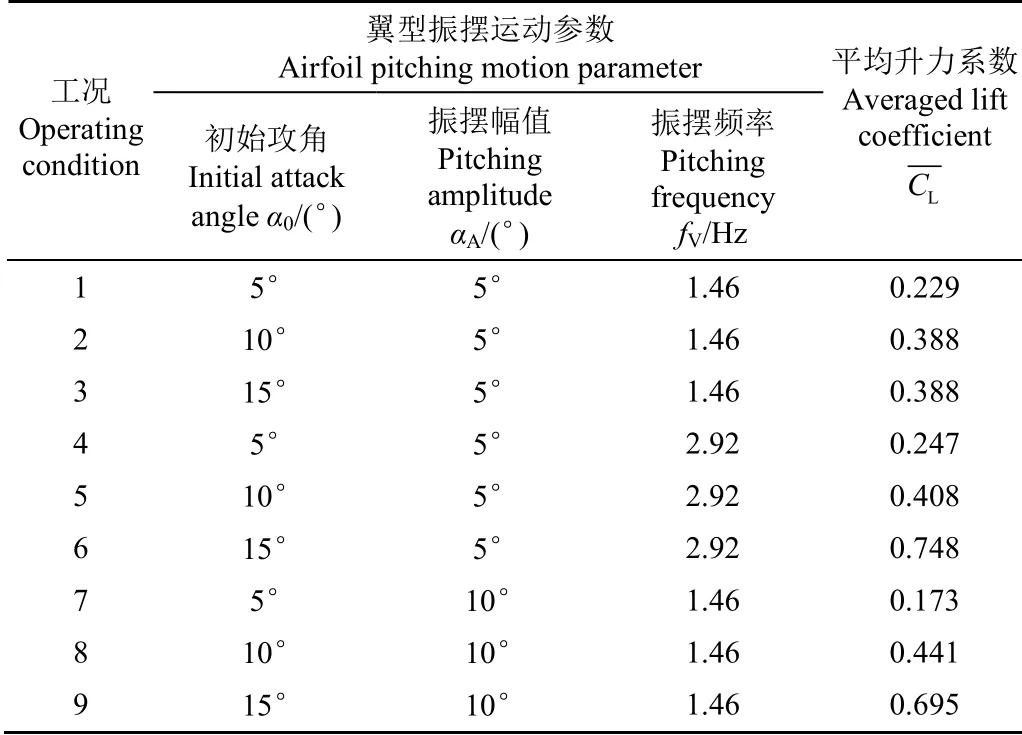
表2 不同工况翼型振摆运动参数及平均升力系数 Table 2 Pitching motion parameters and averaged lift coefficient under various operating conditions

在整个振摆周期中平均升力系数主要受到振摆初始攻角影响，随着的增加，翼型平均升力系数增大。在其余条件相同的情况下，随着振摆频率的增加，平均升力系数均增加，且振摆频率对大初始攻角下的平均升力系数增加的影响更加显著，这与白鹏等研究的结论一致。振摆频率由1.46 Hz增加至2.92 Hz引起=5°情况升力系数增加7.9%，=10°情况升力系数增加5.2%，=15°情况升力系数增加17.2%，对于中、小攻角的影响均在10%以内，但对于大攻角其影响大于10%。与静止情况相比，除=5°与=15°的高频小幅值振摆平均升力系数分别保持不变、增加4.3%外，其余情况均有所减小，减小程度均在13%以内，因=5°低频大幅值振摆中出现负攻角，故不在考虑范围内。

图6与图7分别为在不同初始攻角下翼型进行低频小幅值振摆（工况1～3），高频小幅值振摆（工况4～6），高频大幅值振摆（工况7～9）时的升力系数随时间变化图与频谱图。总体来说，受到翼型振摆的影响，其升力系数均呈现周期性波动的情况，且波动主频均为翼型振摆运动频率，同时频谱图中的出现的次频均为翼型振摆频率的整数倍，说明其升力系数的波动现象的发生均受到翼型振摆频率的影响。

对比图6和图7中不同初始攻角下的情况，随着初始攻角的增加，频谱图中出现的高次次频数量明显增加，升力系数的波动现象更加剧烈。在较大的初始攻角下，出现了更多与相关的倍频，可能是因为较大攻角下翼型绕流中更易发生流动分离形成小尺度旋涡，在振摆的影响下形成翼型表面压力分布的波动。

对比图7a、7b，随着振摆频率增加，在=15°的情况下，升力系数波动频率主频幅值和次频2幅值均显著增加，次频数量明显减少。但是对于较小的初始攻角=5°、=10°，振摆频率的增加减少了次频数量，而对主频和次频幅值的影响较小，说明较大的初始攻角下翼型升力系数波动受高频振摆的影响更为显著。对比图6a、图6b，振摆频率的变化明显改变了中（=10°）、大（=15°）初始攻角时升力系数周期变化的整体趋势。杨筱沛等指出翼型升力系数的变化规律与翼型尾涡脱落规律保持一致，因此振摆频率的增加使较低频波动波峰波谷的数量明显减少，有可能是因为随着振摆频率的增加，当绕流流体通过翼型尾缘处时，翼型边界与流动的相对速度增大，在对流影响下形成的旋涡在尾缘处尚未充分演化便迅速脱落，从而减弱了升力系数的低频大幅值波动。

对比图6a与图6c、图7a与图7c，可以得出振摆幅值对翼型升力系数的影响。在相同振摆频率下，振摆幅值的增加使三种攻角下频谱图中高次次频的数量增加，同时各频率幅值也有所增加。虽然主频幅值基本不受初始攻角影响，但随着初始攻角增大，次频中与相关的倍频增多，这与低频小幅值振摆的情况类似。这表现出在翼型低频振摆情况下，振摆幅值占据主导作用。

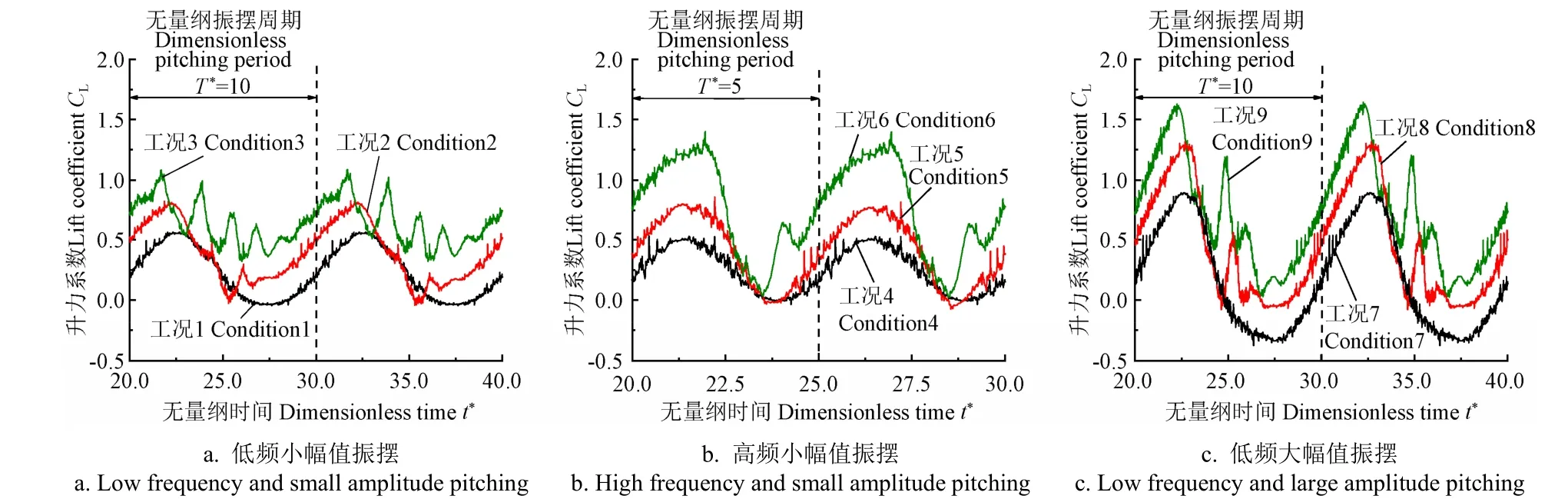
图6 不同工况升力系数变化曲线 Fig.6 Change curves of lift coefficient variation at different conditions

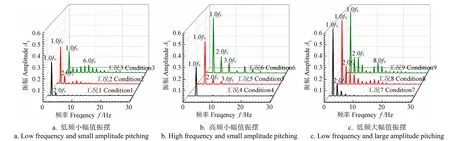
图7 不同工况攻角升力系数频谱图 Fig.7 Spectrum of lift coefficient at different conditions

3.2 升力系数波动与流场演变的相关性

在前文中已经说明翼型升力系数存在周期性波动，以初始攻角=15°，振摆频率=1.46 Hz，振摆幅值=5°的情况为例进行分析，其在一个振摆周期内的速度矢量分布、涡量分布（无量纲）、压力分布（无量纲）见图8。翼型升力系数在单个振摆周期存在着较低频的大幅值波动，引起这种波动的原因可能为压力面尾缘形成的逆时针旋涡在翼型吸力面尾缘处的持续演化发展。

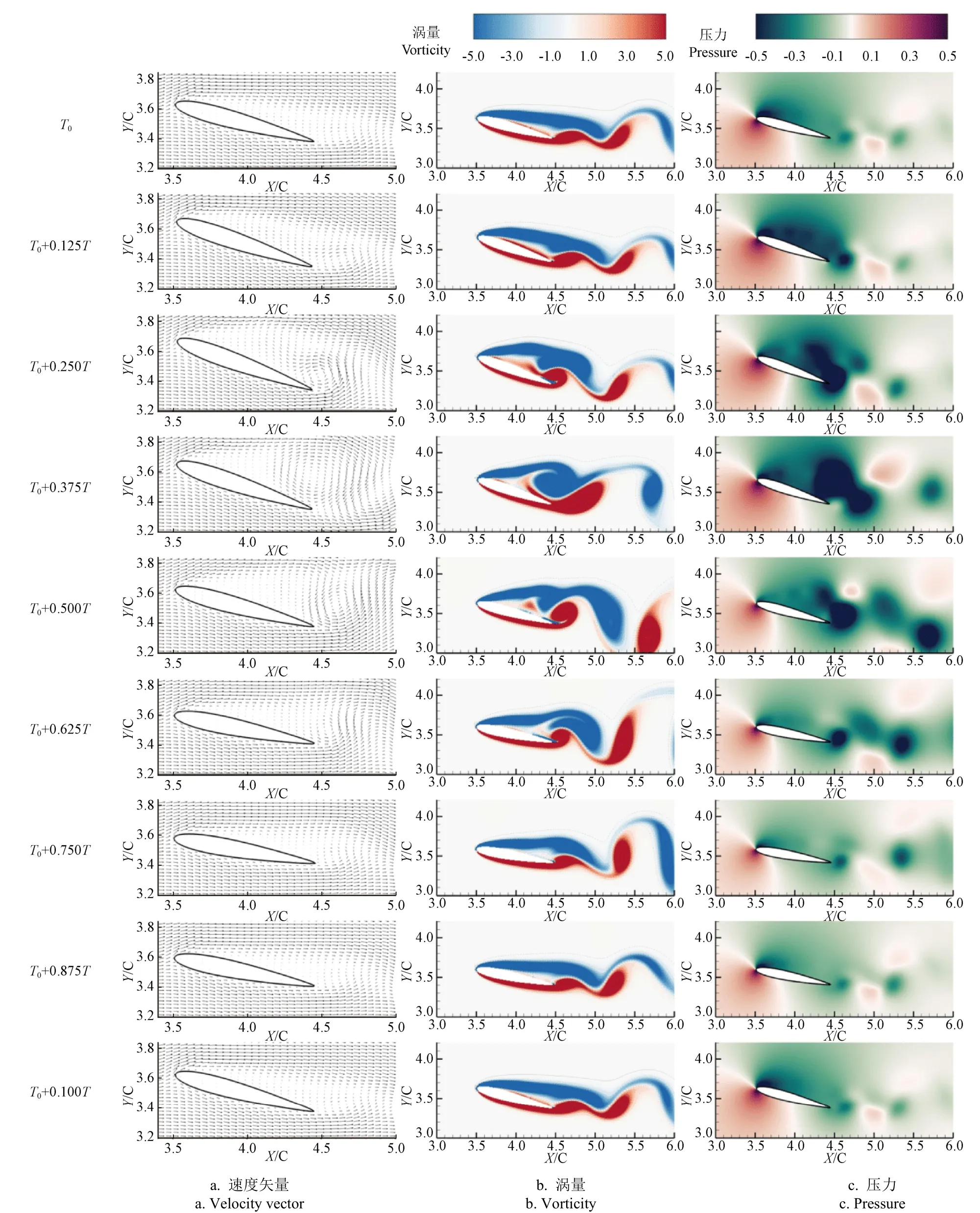
图8 单个振摆周期内速度矢量图、涡量、压力随时间变化分布图 Fig.8 Velocity vector diagram, vorticity and pressure distribution diagram with time in a pitching period

如图8中的涡量分布云图所示，翼型的一个振摆周期中，其压力面均未发生流动分离，壁面边界层流动稳定。至+0.250区间内翼型攻角增加并逐渐达到最大攻角，结合速度矢量与压力分布可知在此期间翼型吸力面前缘处流体速度受到壁面的影响逐渐加剧，形成强烈的逆压梯度，促发了流动分离，同时由于沿壁面法向速度梯度的存在，吸力面前缘处流体受到主流的剪切力，在顺压梯度的驱动下形成顺时针的负值旋涡流动。当翼型攻角发生变化时，受到振摆翼型壁面转动的影响，流体压力场发生变化，尾缘处压力降低诱发压力面近壁流动卷起，形成逆时针正值旋涡流动。至+0.250时刻，翼型尾缘处形成了同时覆盖压力面与吸力面的连续低压区，出现正值旋涡回流至吸力面的情况，并与前缘产生的负值涡相互作用。+0.250至+0.750区间内翼型攻角减小并达到最小攻角，翼型压力面不断有正值逆时针旋涡卷起至吸力面并与阻碍前缘负值旋涡向下游的发展，同时伴随着尾缘处覆盖压力面与吸力面的连续负压区域的出现与消失。单个振摆周期内正负值涡在吸力面中的相互作用主要发生在此区间内，同时由速度矢量图可知在此期间翼型吸力面尾缘上方旋涡流动区域相比于其他时间区间更大。+0.750至+1.000区间内翼型逐渐回到起始攻角，此区间内尾部仍存在交替的脱落涡，但此区间内尾部产生的连续负压区负压值、正负值涡量范围均较小。

图9为初始攻角=15°的低频小幅值振摆（工况3）单个振摆周期升力系数变化曲线图，图10为升力系数处于波峰、波谷时刻的涡量与压力分布云图。由图可见，在升力系数处于峰值的时刻，尾缘处由压力面产生并卷起至吸力面的正值涡均正处于从翼型脱落的过程中，且涡核位置已经脱离尾缘，其所处位置的负压区对翼型表面的压力分布的影响减弱，而此刻吸力面形成的负值前缘分离涡受到卷起涡的阻碍并未脱离，其所在位置仍存在一个负压区，从而导致了翼型两面压力差处于峰值。之后随着压力面下一个的负值涡的产生并卷起至吸力面，并与吸力面负值涡相互作用，诱导出两个负值的分裂涡，单个涡的强度下降，升力系数逐渐下降。在靠近下游的分裂涡从翼型脱落的同时，升力系数达到谷值，由此时的压力分布图可知，此时翼型尾缘处形成了同时覆盖压力面与吸力面的的连续低压区，引起了两面压力差的衰减。此时刻后随着流动的发展，卷起至吸力面的涡经尾缘处脱离，翼型升力系数逐渐增加直至下一个波峰。

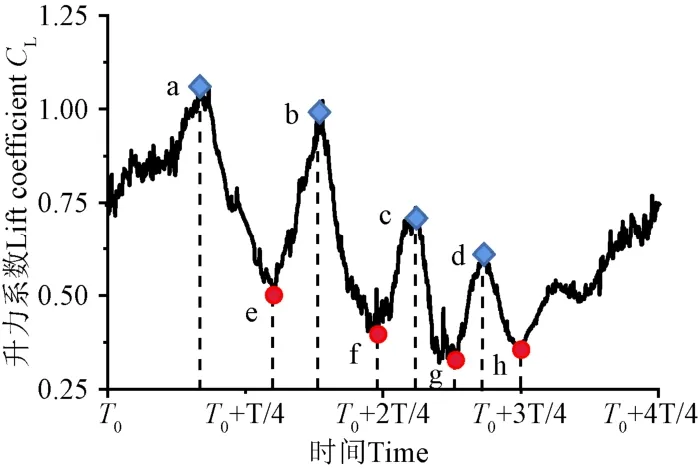
图9 工况3单个周期内升力系数变化曲线 Fig.9 Variation curves of lift coefficient in a single pitching period of condition 3

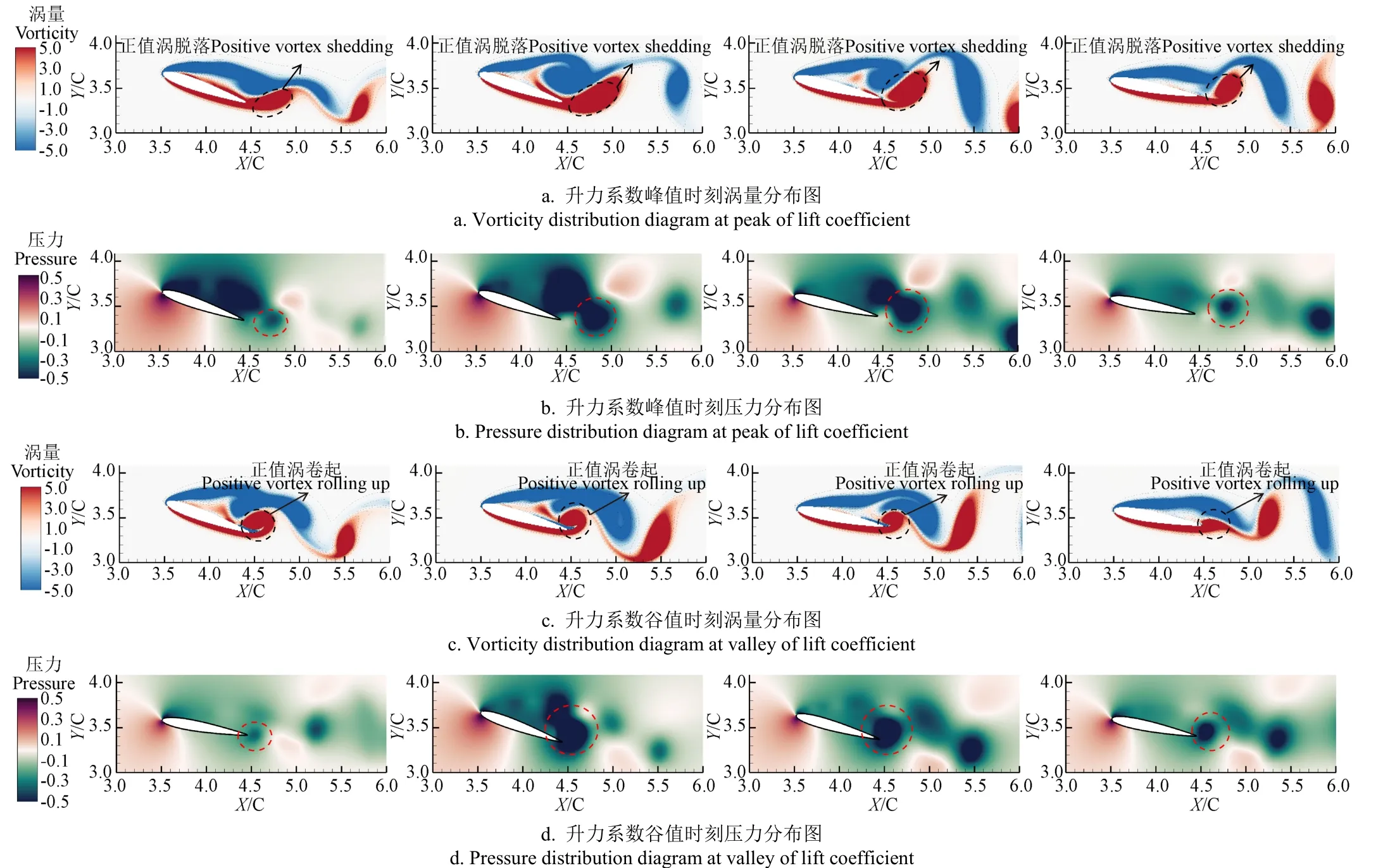
图10 升力系数峰值、谷值时刻涡量及压力分布图 Fig.10 Distribution diagram of vorticity and pressure at peak and valley of lift coefficient

根据汤姆孙定理，正压有势的理想流体绕翼型速度环量不发生变化，而在非理想流体中黏性存在导致的旋涡流动改变了速度环量，升力由绕翼型的逆时针速度环量提供。图11为升力峰值谷值时刻翼型周围流体速度矢量图，由图分析可知，当升力系数处于峰值时刻，尾缘处存在一个顺时针的旋涡流动，在壁面处其速度方向与来流方向相反，从而导致了绕翼型逆时针速度环量增加，进而提高了翼型的升力；当升力系数处于谷值时刻，翼型尾缘处仅存在一个逆时针的旋涡流动，此流动的存在减弱了速度环量，导致了翼型升力的衰减。

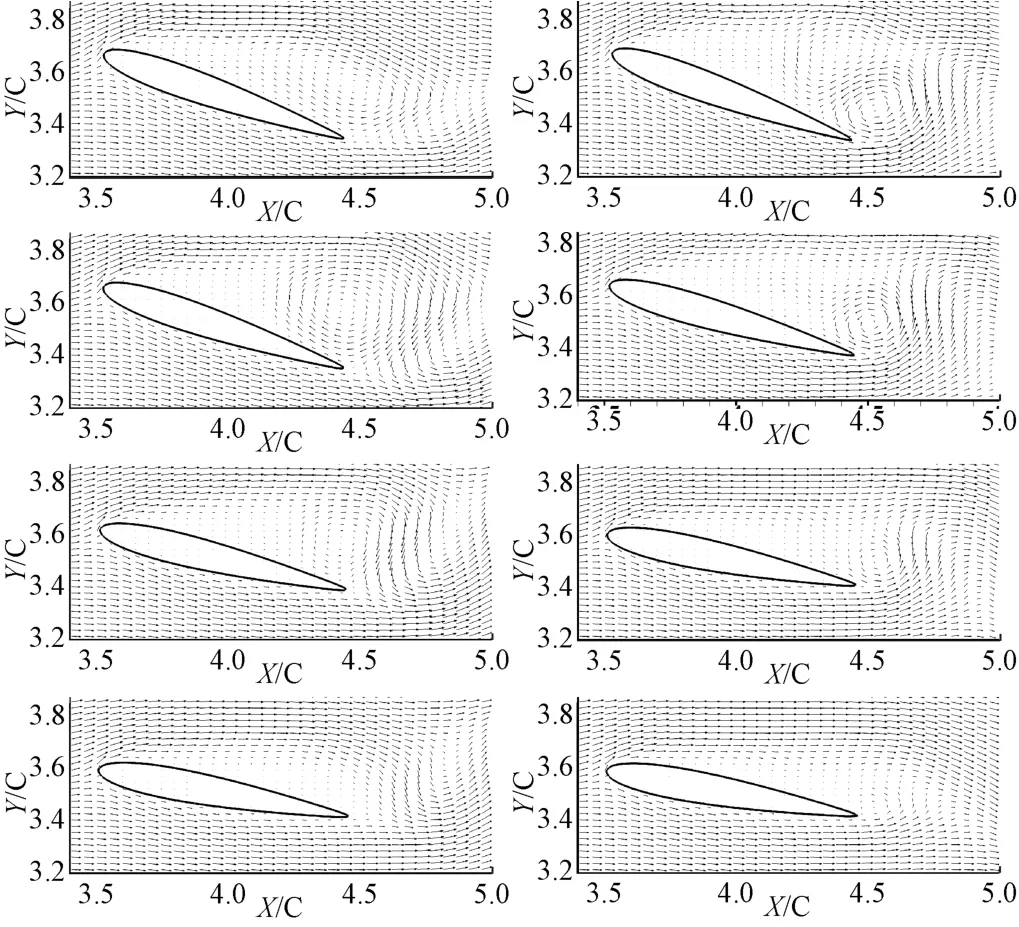
图11 升力系数峰值、谷值时刻速度矢量分布图 Fig.11 Distribution diagram of velocity vector at peak and valley of lift coefficient

因此，翼型在振摆过程中出现的升力大幅值波动的原因为压力面逆时针旋涡由翼型尾缘分离后卷起至压力面发展成逆压梯度流动，形成正值涡量，与翼型吸力面流动分离脱落的负值涡旋涡发生强烈相互作用，在此过程中导致翼型壁面压力分布剧烈变化引起了升力的大幅值波动。分析结果可为翼型振摆过程中的升力不稳定性问题的解决提供一定思路。