基于MBD-DEM耦合的联合收获机割台仿形机构设计与试验

金诚谦，刘岗微，倪有亮，杨腾祥，王廷恩，齐彦栋

（1. 农业农村部南京农业机械化研究所，南京 210014；2. 山东理工大学农业工程与食品科学学院，淄博 255000）

0 引 言

联合收获机的使用大幅提高了收获效率、降低了劳动强度，但国内现有联合收获机信息化、智能化技术配备较少，主要作业参数仍然依靠手动操纵杆调控，操控不便。

割台高度作为联合收获机作业的关键参数，设置过高时易引起较大的谷物漏割损失，设置过低时易导致割台铲土、降低割台使用寿命。国内外学者针对割台高度自动调控问题，对联合收获机割台仿形系统进行了相关研究。Xie等分析了割台高度控制系统存在的基本限制，提出一种机械系统与控制器一体化设计的方法，提高了鲁棒性。Tulpule等基于IROD（Integrated Robust Optimal Design）方法设计了联合收获机割台高度控制系统，Kassen等通过RFL（Robust Feedback Linearization）方法在提高割台高度控制系统鲁棒性的同时降低了控制系统功耗。Ni等基于土壤-机器系统设计了大豆联合收获机割台高度自适应调控系统，割台仿形控制精度达92%。杨术明等提出一种基于超声波传感器的割台高度控制系统，但在作业过程中易受杂草、土块影响。伟利国等设计了一种接触式机械仿形机构和割台地面仿形控制系统，割台高度控制误差小于12 mm，但仿形板主要依靠自身重力保持与地面接触，当地面起伏较大或作业速度较快时，仿形板易出现弹跳现象，导致较大的割台高度检测误差。张聪重点研究了传感器数据滤波处理和多传感器融合算法，使用BP神经网络数据融合方法得到精度较高的割台高度测量数据。耿爱军等为实现玉米联合收获机割台高度自动调控，设计了浮动压紧式仿形机构和PID控制系统，试验表明割台高度调控误差小于20 mm。上述文献主要侧重于割台仿形系统控制策略和控制算法研究，对割台仿形机构机械结构设计和研究相对较少，割台高度调控精度较差。

针对国内现有割台仿形机构对田间地面仿形精度低的问题，本文设计一种主-副板压紧式割台仿形机构，基于多体动力学（Multi-Body Dynamics, MBD）和离散元法（Discrete Element Method, DEM）耦合，采用Adams和EDEM软件联合仿真，模拟仿形机构工作过程，设计四因素二次回归通用旋转组合优化试验，探究最优设计参数组合，并进行田间试验验证，为联合收获机割台仿形机构设计提供借鉴。

1 总体结构与工作原理

1.1 总体结构

割台仿形机构的功能是感知地面起伏变化信号并通过角度传感器输出。本文以4GW-1.6型谷物收获割台（主要参数如表1所示）为基础，设计主-副板压紧式仿形机构，主要由割台、主仿形板、副仿形板、弹簧、角度传感器和四连杆传动机构组成，基本结构如图1所示。主仿形板上端与割台底板铰接于割刀下方，下端与副仿形板铰接，主、副仿形板之间由两条对称布置的弹簧连接，主仿形板与角度传感器之间通过四连杆机构传动。

表1 4GW-1.6型谷物收获割台主要参数 Table 1 Main parameters of 4GW-1.6 grain harvester header

图1 主-副板压紧式仿形机构 Fig.1 The main-subplate pressing profiling mechanism

1.2 工作原理

仿形机构作业时，副仿形板上端在弹簧拉力作用下始终保持与割台底板接触，主仿形板在自身重力、弹簧拉力和副仿形板的共同作用下始终保持与地面接触，以感知地面起伏变化。地面隆起时，主仿形板在地面支持力作用下顺时针转动，割台高度降低，角度传感器转角变大。地面凹陷时，主仿形板逆时针转动，割台高度升高，角度传感器转角减小。

2 关键部件设计

2.1 主、副仿形板

作业时主、副仿形板分别与土壤、割台底板接触摩擦，为防止仿形板锈蚀损坏，其材料选用301不锈钢。为减小土壤和主仿形板间的摩擦阻力，减小副仿形板上端和割台底板间的摩擦力，主仿形板底部和副仿形板上端设计为圆弧形状。

主、副仿形板宽度和长度是仿形机构的关键参数。若仿形板宽度设计过小，地面凹陷或割台升高时易使仿形机构脱离地面，无法准确感知地形变化；仿形板长度设计过大会增加仿形机构重量，使土壤下陷距离增大，仿形精度变差。根据表1，设计主仿形板与副仿形板宽度（W、W）各为割台底板宽度的二分之一，即W=W= 200 mm。割台左右两侧各布置一组仿形机构，根据割台底板长度尺寸，选取主、副仿形板长度范围为350～750 mm。

2.2 弹簧

弹簧是保证仿形机构正常作业的关键部件，其主要参数包括刚度系数和初始长度L。若弹簧力设计过小，副仿形板易脱离割台底板，主仿形板易产生弹跳现象，无法实时感知地形变化；弹簧力设计过大，会增大副仿形板与割台底板、主仿形板与地面间的作用力，导致仿形机构转动困难。

根据主仿形板转角确定弹簧初始长度取值范围。建立如图2所示的几何模型，当主仿形板转角最大时，弹簧初始长度L取得最大值，即：

图2 仿形机构几何模型 Fig.2 Geometric model of profiling mechanism

由仿形机构机械结构设计可知，主仿形板转角范围为18°～56°，则L<0.11 m，初步确定L为80～110 mm。

为确定弹簧刚度系数的取值范围，建立如图3所示的仿形机构力学分析模型。铰接点和土壤支持力（F,F）作用点之间距离很小，在力学分析时忽略铰接点处作用力F、F、F、F对点的力偶矩（M,M），同时忽略各铰接点处的摩擦力。根据理论力学平面任意力系平衡条件，主-副仿形板整体平衡方程为

图3 仿形机构受力分析 Fig.3 Force analysis of profiling mechanism

式中为割台和副仿形板间滑动摩擦系数，取=0.18，为主仿形板和土壤间滑动摩擦系数，取=0.11。

副仿形板平衡方程为

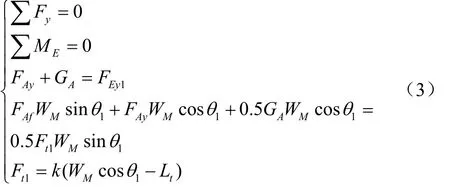
主仿形板平衡平衡方程为

联立式（2）～（4），解得：

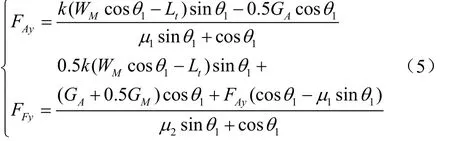
仿形机构作业时，使副仿形板上端不脱离割台底板的条件是F>0，则>295 N/m。为确保作业过程中副仿形板始终与割台底板保持接触，初步确定弹簧刚度系数取值范围为300～800 N/m。

2.3 仿形机构运动分析

主-副板压紧式割台仿形机构采用角度传感器转角大小表征割台高度值。采用复数矢量法分析仿形机构各杆件之间相对运动关系，以探究主仿形板与角度传感器的角位移传动关系。

由图2可知，仿形机构的封闭复数矢量方程为

按欧拉公式展开，实部与虚部分别相等，即

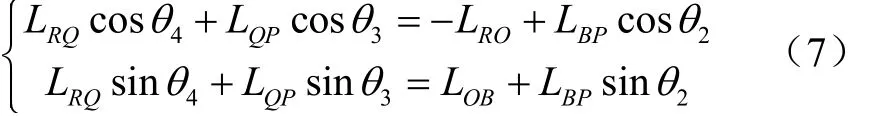
消去，化简为

代入三角函数万能公式，根据图1所示仿形机构各杆件初始位置，解得：

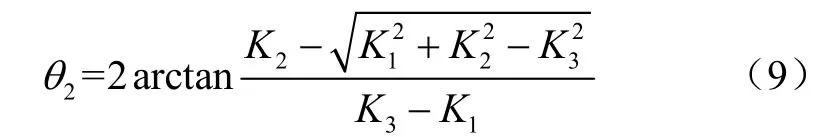
根据图2，=，则割台高度计算公式为

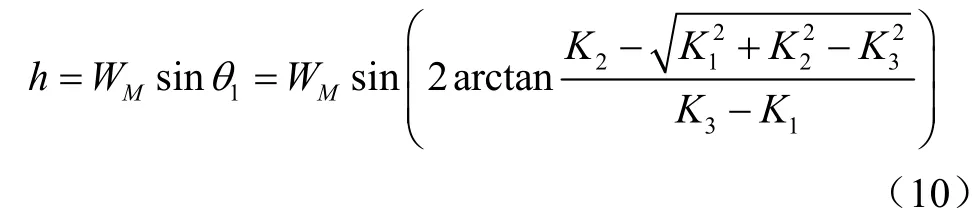
3 参数优化

使用Design-Expert软件设计四因素二次回归通用旋转组合试验优化仿形机构关键参数。

主仿形板与副仿形板的相互作用涉及多体动力学理论，与土壤的相互作用涉及动力学理论和离散元理论，故采用MBD-DEM耦合仿真方法进行响应面试验。

3.1 试验方案

在响应面优化试验中要求试验点包含各因素最佳水平。根据式（5），确定试验因素为弹簧刚度系数、弹簧初始长度L、副仿形板长度L和主仿形板长度L。运用标准粒子群优化算法对F的数学模型进行优化。根据仿形机构工作条件，设定约束条件为F>0，F>0，优化目标为F的最大值尽量小。优化结果：弹簧刚度系数=402.03 N/m，弹簧初始长度L=0.103 m，副仿形板重力G=14.7 N，主仿形板重力G=49 N。此时，副仿形板长度L=581 mm，主仿形板长度L=562 mm。以粒子群算法优化结果为各因素中心水平，根据经验确定各因素其他水平，如表2所示。

表2 试验因素和水平 Table 2 Factors and levels of experiments

在响应面试验中对F最大值进一步优化。如图4所示，将粒子群算法优化结果代入式（5），以主仿形板转角为自变量绘制F曲线。由图4可知，F值均大于0，且在=0.585 rad处取最大值53.4 N，根据式（10），此时割台高度为11 cm。因此，MBD-DEM耦合仿真试验中，设置割台高度为11 cm。

图4 土壤对主仿形板支持力随主仿形板的变化 Fig.4 Variation of supporting force of soil to main profiling plate with rotation angle of main profiling plate

根据仿形机构工作原理及上述分析，选取割台对副仿形板的支持力F、土壤对主仿形板的支持力F和土壤下陷距离L为优化试验的评价指标。

F表征仿形机构是否处于正常工作状态。若F<0，说明副仿形板脱离割台底板，此时主仿形板易产生弹跳现象，仿形机构处于失效状态；若F>0，说明仿形机构工作正常。F表征仿形机构对地形变化感知的灵敏度。若F较大，说明需要较大的土壤作用力才能迫使主仿形板转动，即仿形机构对田间地形变化感知较“迟钝”，反之说明仿形机构对田间地形变化感知较“灵敏”。L指标表征仿形准确性。若L较小，说明土壤受主仿形板作用力下陷较小，仿形机构对田间地形仿形准确度较高。

3.2 MBD-DEM耦合仿真建模

在Adams View环境中建立主-副板压紧式仿形机构的多体动力学模型，各部件间的运动副设置如表3所示。为防止仿形板锈蚀损坏，主、副仿形板材料配置为不锈钢，其余部件材料选用普通碳钢。在割台和大地间添加滑移副，模拟收获机前进，参考大豆联合收获机实际作业速度，设置驱动速度为1 m/s。在主仿形板和副仿形板间添加弹簧柔性连接表示拉伸弹簧。在主仿形板和土壤之间添加广义力General Force以测量F，在副仿形板与割台底板接触位置添加Marker点以测量F，在主仿形板与土壤接触位置添加Marker点以测量L。

表3 多体动力学模型运动副配置表 Table 3 Kinematic pair configuration table of multi-body dynamics model

运用EDEM软件建立如图5所示的离散元模型，在主仿形板下方建立土壤颗粒床，大小为2 000 mm× 1 000 mm×100 mm（长×宽×高）。

图5 离散元模型 Fig.5 Discrete element model

接触模型是离散单元法的重要基础，对于不同的仿真对象，必须建立不同的接触模型。EEPA（Edinburgh Elasto-Plastic Adhesion）接触模型包含了颗粒的塑性和黏性，适宜于模拟可塑性强的农田土壤。将土壤-土壤颗粒接触模型设定为EEPA接触模型，参考EDEM软件土壤仿真例程，将土壤-主仿形板接触模型设定为Hertz-Mindlin With JKR接触模型。根据土壤颗粒物理特性离散元参数标定相关文献，土壤颗粒仿真参数配置如表4所示。

表4 土壤颗粒离散元参数配置表 Table 4 Parameter configuration table of discrete element for soil particles

进行MBD-DEM耦合仿真试验时，每次试验前采取重新生成土壤颗粒床的方式体现仿真试验的随机性。在试验后将耦合仿真结果文件导入Adams PostProcessor模块，剔除仿真开始阶段波动较大的数据，取0.5～1 s之间的数据平均值作为响应指标结果。试验方案与结果如表5所示。

表5 试验方案与结果 Table 5 Experimental scheme and results

3.3 结果分析

根据表5数据，对试验结果用Design-Expert软件进行多元回归拟合，分别建立割台对副仿形板支持力F、土壤对主仿形板支持力F、土壤下陷距离L与各因素的二次多项式回归模型，如式（11）～（13）所示。

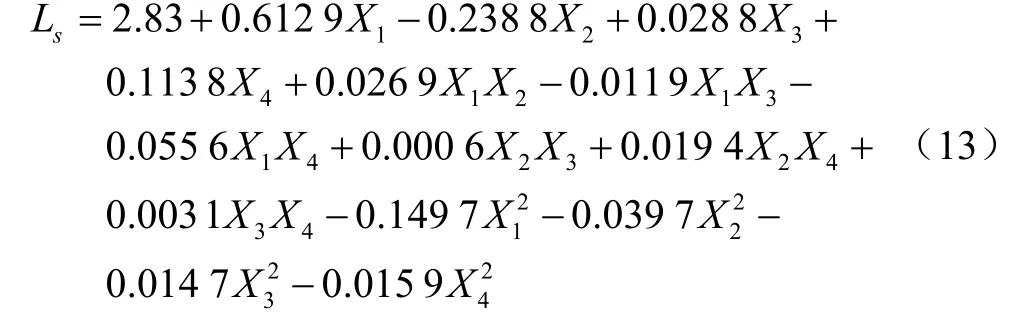
回归模型方差分析和显著性检验结果如表6所示。由表6可知，割台对副仿形板的支持力F、土壤对主仿形板的支持力F和土壤下陷距离L回归模型极显著（模型<0.001），且失拟项不显著（失拟项>0.05），表明回归方程拟合度较好，且不存在其他影响响应指标的主要因素，可以通过该模型对仿形机构的设计参数进行分析与优化。

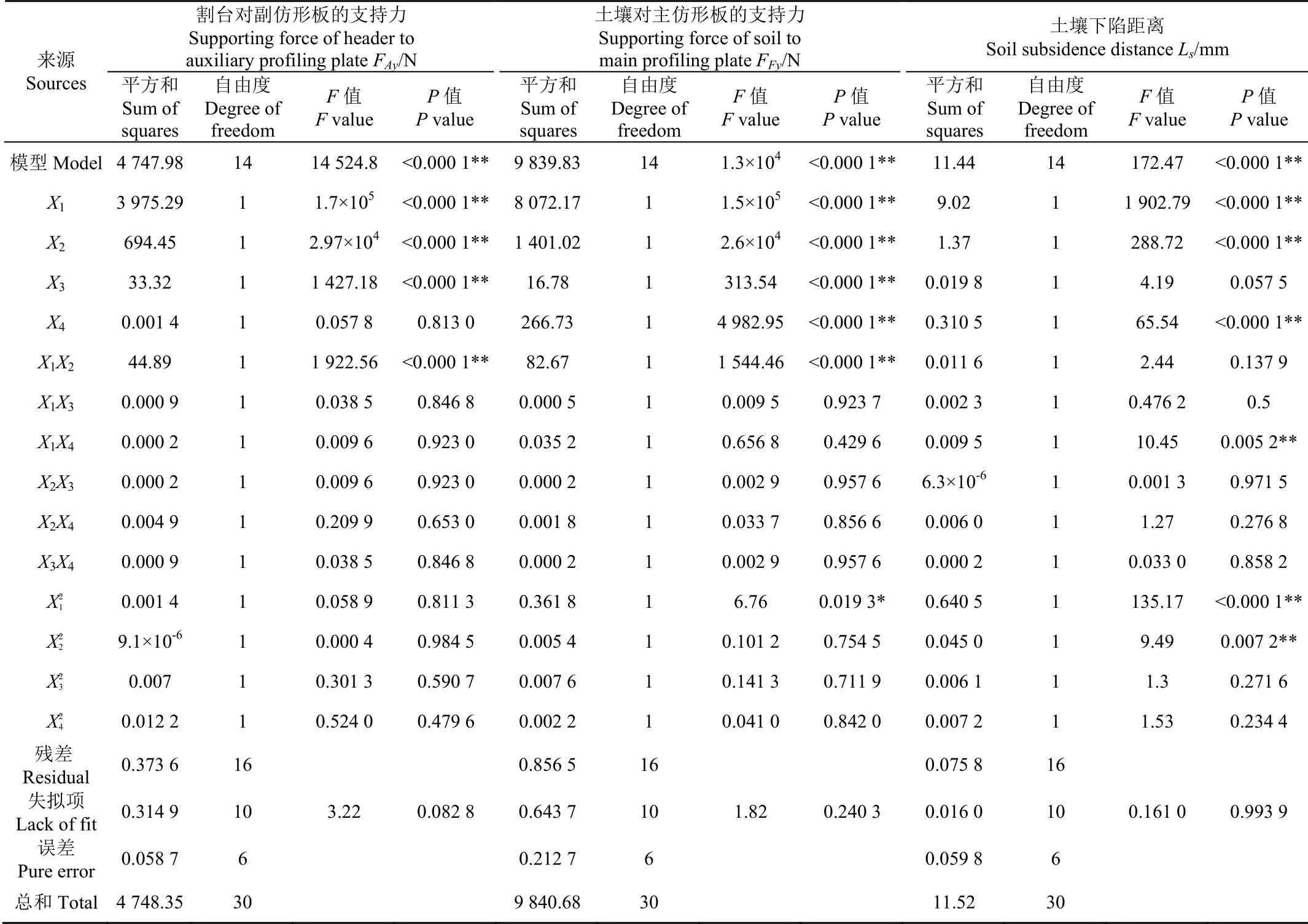
表6 回归方程方差分析 Table6 Variance analysis of regression equation

各回归项对回归模型的影响显著性可由值大小确定。F回归模型中，一次项、、及交互作用项影响极显著（<0.01）；F回归模型中，一次项、、、及交互作用项影响极显著（<0.01），二次项影响显著（<0.05）；L回归模型中，一次项、、，交互作用项及二次项、影响极显著（<0.01）。在保证模型显著、失拟项不显著的前提下，剔除不显著回归项，回归方程优化结果为

通过对式（14）～式（16）的回归系数检验可知：各因素对F影响显著性从大到小为、、、，对F和L影响显著性从大到小为、、、。弹簧刚度系数和弹簧初始长度是3个响应指标的主要影响因素。

3.4 响应曲面分析

利用Design-Expert软件绘制交互因素对试验指标的影响曲面图，如图6所示。

由式（14）及图6a可知，副仿形板长度为581 mm，主仿形板长度为562 mm时，弹簧刚度系数各水平下，弹簧初始长度与割台对副仿形板的支持力负相关，较优的弹簧初始长度为90～100 mm；弹簧初始长度各水平下，弹簧刚度系数与割台对副仿形板的支持力正相关，较优的弹簧刚度系数为500～650 N/m。当弹簧初始长度为90 mm，弹簧刚度系数为650 N/m时割台对副仿形板的支持力最大，为54.96 N。

由式（15）及图6b可知，副仿形板长度为581 mm，主仿形板长度为562 mm时，弹簧刚度系数各水平下，弹簧初始长度与土壤对主仿形板的支持力负相关，较优的弹簧初始长度范围为100～110 mm；弹簧初始长度各水平下，弹簧刚度系数与土壤对主仿形板的支持力呈正相关性，较优的弹簧刚度系数为350～500 N/m。当弹簧初始长度为110 mm，弹簧刚度系数为350 N/m时土壤对主仿形板的支持力最小，为64.28 N。

由式（16）及图6c可知，弹簧初始长度为100 mm，副仿形板长度为581 mm时，主仿形板长度各水平下，弹簧刚度系数与土壤下陷距离正相关，较优的弹簧刚度系数为350～500 N/m；弹簧刚度系数各个平下，主仿形板长度与土壤下陷距离正相关，较优的主仿形板长度为450～562 mm。土壤下陷距离大于3 mm时，弹簧刚度系数和主仿形板长度的改变对土壤下陷距离影响较小，这是由于随着土壤深度增加，土壤紧实度增大，土壤下陷距离减小。当弹簧刚度系数为350 N/m，主仿形板长度为450 mm时土壤下陷距离最小，为1.87 mm。

图6 交互因素对各指标的影响 Fig.6 Effects of interaction factors on indices

3.5 参数优化

根据仿形机构工作条件，要求弹簧拉力尽量大，以保证主仿形板与地面始终保持接触，实时感知地形变化；为提高仿形机构感知地形起伏变化的灵敏度，要求土壤对主仿形板的支持力F尽量小；为提高仿形机构检测割台高度的精度，要求土壤下陷距离L尽量小。为获得仿形机构较优工作性能的设计参数，建立参数优化模型，目标函数和约束条件为

使用Design-Expert软件优化模块求解模型较优的参数组合。当弹簧刚度系数为464 N/m、初始长度为90 mm、副仿形板长度为484 mm、主仿形板长度为450 mm时，割台对副仿形板的支持力为38.2 N，土壤对主仿形板的支持力为86.57 N，土壤下陷距离为2.72 mm。

结合优化结果，对弹簧进行设计选型。根据仿形机构弹簧的工况特点，弹簧材料选择碳素弹簧钢丝，为提高材料利用率，弹簧旋绕比取10，主要参数计算公式为

式中为弹簧初始长度，mm；为弹簧有效圈数；为弹簧丝直径，mm；为弹簧刚度系数，N/m；为弹簧丝的切变模量，Pa；为弹簧旋绕比。计算得到弹簧丝直径2 mm，外径20 mm，有效圈数45圈。

4 田间试验

4.1 试验条件与设备

对主-副板压紧式仿形机构最优设计参数组合进行田间验证试验。试验于2021年6月在山东省临沂市相公镇进行，试验田土壤为棕壤土，质地均匀，地面平整，含水率12.4%，坚实度0.067 N/mm。

如图7a所示，试验设备主要包括联合收获机、割台、仿形机构和数据采集系统。数据采集系统主要由数字变送器（欧路达TDA-04D2数字变送器，综合精度0.01%）、主仿形板压力传感器、副仿形板压力传感器（承映HZC-B01拉杆式拉压力传感器，输出信号0～20 mV，综合精度0.3%）和数据记录组态屏组成。数字变送器将压力传感器0～20 mV电信号转换为压力值并通过RS485总线发送到数据记录组态屏，压力数据通过组态屏记录到U盘内。主仿形板压力传感器用于采集土壤对主仿形板的支持力F，副仿形板压力传感器用于采集割台对副仿形板的支持力F。

如图7b所示，为增大传感器受力面积，在无螺纹端安装小圆板。分别在副仿形板与割台底板接触位置和主仿形板与土壤接触位置开孔，使用螺栓将压力传感器紧固到仿形板上。每次试验前，使用组态屏对压力传感器进行置0操作，以保证测量准确度。

图7 试验设备与场景 Fig.7 Test equipment and scene

4.2 试验指标与方法

田间验证试验指标为割台对副仿形板的支持力F、土壤对主仿形板的支持力F和土壤下陷距离L。试验时，根据MBD-DEM耦合仿真试验条件，设置割台高度为11 cm，驾驶联合收获机以1 m/s的速度向前行驶15 m，重复试验3次。

如图8所示，每次试验后，沿仿形板运动方向以1 m间隔选取10个测量点，在每个测量点沿横向随机选取5点，以仿形板边缘外侧土壤未下陷区为测量基准，使用直尺测量内侧各点土壤下陷距离，求出平均值，记为该测量点的土壤下陷距离值。

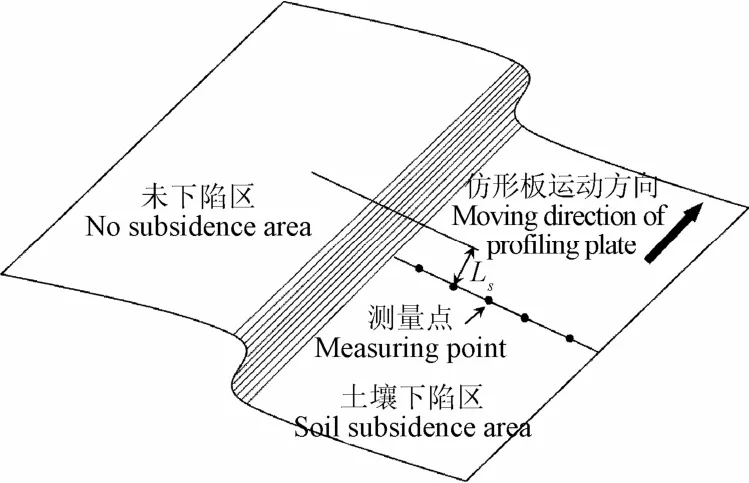
图8 土壤下陷距离测量示意图 Fig.8 The schematic diagram of soil subsidence distance measurement

4.3 试验结果与分析

F和F的测试曲线如图9所示。试验时，由于收获机自身振动和田间地形随机变化导致F、F数据曲线出现抖动。3次重复试验中F结果均大于0，说明在作业过程中副仿形板始终与割台底板接触，仿形机构处于正常工作状态。F平均值分别为85.23、85.80、86.08 N，与优化结果86.57 N相接近，表明参数优化模型较可靠，土壤仅需较小的作用力即可驱使主仿形板转动，仿形机构对田间地形起伏变化感知的灵敏度较高。

图9 仿形板受力测试曲线 Fig.9 Test curves of force on profiling plate

L结果如表7所示。根据表7，L数据分布在3～12 mm之间，由于试验田地土壤紧实度与仿真土壤颗粒床不同，导致田间试验L结果略大于参数优化模型预测结果。3次重复试验中L平均值分别为5.4、7.1和6.4 mm，均小于10 mm，表明作业时土壤下陷距离较小，仿形机构对田间地形感知准确度较高。

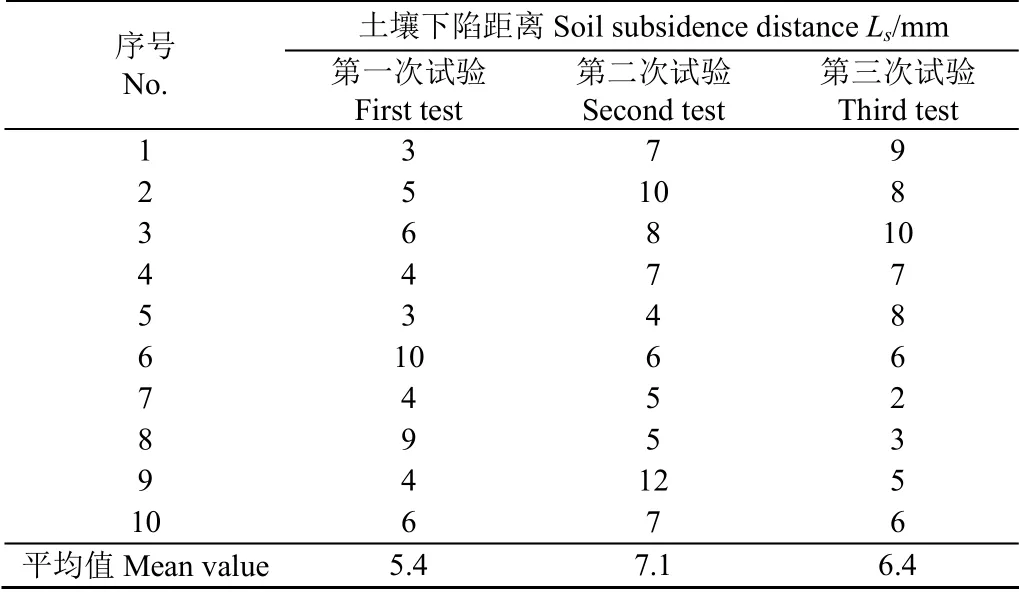
表7 土壤下陷距离试验结果 Table 7 Test results of soil subsidence distance

5 结 论

1）为提高割台仿形机构对田间地形起伏变化感知的灵敏度，设计了一种主-副板压紧式割台仿形机构。在分析工作原理的基础上，建立了几何模型和力学分析模型，可为割台仿形机构的结构设计与优化提供参考。

2）采用MBD-DEM耦合仿真方法，分别建立了仿形机构多体动力学仿真模型和离散元仿真模型。设计四因素二次回归通用旋转组合优化试验，得到割台对副仿形板的支持力、土壤对主仿形板的支持力、土壤下陷距离与弹簧刚度系数、弹簧初始长度、副仿形板长度、主仿形板长度的数学回归模型。以割台对副仿形板的支持力取值尽量大、土壤对主仿形板的支持力取值尽量小，土壤下陷距离取值尽量小为优化目标，得到最优设计参数组合为：弹簧刚度系数464 N/m，弹簧初始长度90 mm，副仿形板长度484 mm，主仿形板长度450 mm。主、副仿形板材料宽度200 mm，长度为301不锈钢。弹簧材料为碳素弹簧钢丝，直径2 mm，外径20 mm，有效圈数45圈。

3）对最优参数组合进行田间试验。3次重复试验中，土壤对主仿形板的平均支持力分别为85.23、85.80和86.08 N，对应的土壤平均下陷距离分别为5.4、7.1和6.4 mm，均小于10 mm。试验结果与优化模型预测值相吻合，表明主-副板压紧式割台仿形机构能够灵敏地感知田间地形变化，具有较高的仿形准确度，可为联合收获机割台仿形系统研究提供参考。