考虑居民用户参与度不确定性的激励型需求响应模型与评估

郑若楠，李志浩，唐雅洁，倪筹帷，李国杰，韩 蓓

（1. 电力传输与功率变换控制教育部重点实验室（上海交通大学）,上海市 200240；2. 国网浙江省电力有限公司电力科学研究院,浙江省 杭州市 310014）

0 引言

近年来,以需求响应（demand response,DR）为典型代表的“源-网-荷互动”技术受到广泛关注［1］。传统DR 资源大多来自负荷占比较大的工业园区［2］,而居民用户地理位置分散、行为模式不一以及传统家用电器的低功耗特性限制了其参与响应的能力。在“碳达峰”和“碳中和”的重要任务下［3］,分布式光伏（PV）、电动汽车（EV）和储能系统（ESS）等多种绿色可调资源大量进入家庭［4］,推动居民侧可控负荷比例持续增加,其参与DR 的潜力亟待深入挖掘。

以智能家庭能量管理系统（smart home energy management system,SHEMS）为代表的智能用电服务终端逐渐成为用户与电网双向互动的核心环节［5］。用户能够通过SHEMS 管理达到经济节能和舒适用电的目的,同时可参与电网DR 项目［6］进一步提高电力系统的可靠性与灵活性。尤其在分布式新能源高渗透的场景下,智能终端的优化控制是提高消纳能力的有效手段［7］。目前对SHEMS 优化模型的研究多以用户侧经济性和舒适性为目标［8］,已有学者在节省家庭用电费用的经济性目标中考虑了基于分时电价［9］、实时电价［10］等机制的价格型DR。然而,由于目前国内激励机制尚不完善,关于激励型DR 的深入研究较为缺乏［11］。有部分研究在优化模型中直接加入负荷波动平抑［12］、削峰填谷［13］、新能源消纳［14-16］等激励型DR 目标,但将其视作强制性目标的处理方式较难实践应用。事实上,在激励型DR 项目的实施过程中,可能出现用户消费心理和行为的变化,使得用户的实际响应情况存在较大不确定性,从而显著影响电网侧调度计划的制定和居民侧实际响应能力的评价。因此,在激励合同与优化模型的设计中考虑用户响应意愿的不确定性具有重要意义。

科学合理的响应能力评估有助于指导电网制定调度计划,完善电价和激励机制。评估方法有自上而下和自下而上两种［17］。现有研究多采用自上而下的评估方式,这种方式下可能出现传输时延、数据损坏和破坏用户隐私［18-21］的问题。SHEMS 良好的双向通信性能为合理就地利用数据、自下而上评估需求侧潜力创造了条件。然而,目前研究仍存在以下问题:多聚焦于对某一时间断面上的负荷增长与削减能力进行评价,对负荷塑形、分布式可再生能源消纳等具有时序特征的持续性响应能力缺乏有效的评估方法［21-22］；现有研究多在价格型DR 层面探索,缺乏针对激励响应能力的深入研究［23］；居民响应能力与个人习惯、激励水平等随机模糊因素［24］相关而具有较强可变性,难以量化为确定性评估指标；多局限于对响应容量等直观效益的评价,而少有文献考虑电网和用户付出的代价,无法衡量边际效用［7］。

本文首先设计了一种优化净负荷曲线的激励型DR 合同,然后结合用户参与激励型DR 的自主能动性优势改进SHEMS 优化模型。进而提出基于参数空间包络域期望的响应能力量化方法,以考虑居民响应行为的不确定性,有效评估其持续性响应能力。基于此,提出综合考虑电网激励成本和用户响应成本的响应能力梯度评估指标,可指导售电公司激励机制的设计与用户响应方案的决策。最后,在MATLAB 仿真平台验证了所提SHEMS 优化模型和评估方法的有效性。

1 考虑激励型需求响应用户参与度的智能家庭能量管理模型

1.1 SHEMS 结构

SHEMS 管控的智能住宅可支持配备多种可参与需求响应的灵活性设备,其工作原理如附录A 图A1 所示。智能住宅通过智能电表监测电器设备的耗电数据,并通过无线网络［25］将负荷用电信息传输至SHEMS 终端。SHEMS 的嵌入式系统可以通过智能电表的监测数据或人机交互终端的参数设置判断设备的灵活性类型。同时,由SHEMS 对智能插座发送局部控制信号以执行能量管理策略。此外,SHEMS 通过网关［26］与售电公司实现信息交互,接收其发布的DR 信号。在通信系统提供家庭负荷需求、光伏发电量及市场电价、DR 信息的基础上,嵌入式系统执行考虑价格型和激励型DR 的能量管理算法,进而生成各类家庭柔性负荷的最优运行方案。

1.2 家用设备分类建模

本文考虑含有分布式PV 装置、ESS、EV 及各种常见家用设备的复杂家庭用电环境。根据用电特征与灵活性程度,将设备分为可转移设备（shiftable appliance,SA）、可中断设备（interruptible appliance,IA）及不可控的基本设备（basic appliance,BA）。日前调度优化区间为1 天,分为T个时段,单个时段长为τ。家用设备的数学模型见附录A 式（A1）至式（A20）。

1.3 考虑用户参与度的目标函数及约束条件

激励型DR 基于事先签订的合同,由电力公司向用户直接发送控制信号,以达到特定的响应目标。而价格型DR 则通过价格信号引导用户自行调整用电行为。本文将以上两种DR 都考虑到SHEMS 目标中。

首先,为鼓励居民实现分布式能源发电最大程度就地消纳,减小对电网的影响,本文设计一种激励型DR 合同以优化家庭净负荷曲线。售电公司和用户双方遵循如下约定:用户可于日前自主决策是否参与次日负荷曲线优化；协议周期内根据用户的实际响应容量定期发放激励补贴；对签订合同的用户“只奖不罚”,即不设置参与度过低惩罚。

对签订以上激励合同的智能用户,SHEMS 应设计用户自主决策型净负荷曲线优化目标。对于一般用户而言,降低其净负荷功率波动可以减小对电网的影响；而对于装设分布式PV 系统的用户而言,尽可能就地消纳的目标也可以通过对家庭净负荷削峰填谷实现。因此,利用全天净负荷方差计算负荷波动水平。

首先,构建考虑用户参与意愿的激励型DR 函数。

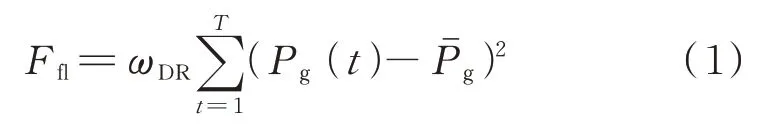
式中:Pg(t)为t时刻用户净负荷,由功率平衡约束得到,见附录A 式（A21）；Pˉg为全时段净负荷平均功率；ωDR为日前由用户自主决策的参与度系数,取值在［0,1］区间内,为1 时表示全力参与激励型DR,为0 时表示该用户不参与激励型DR。

其次,在分时电价机制下,SHEMS 计算全天家庭用电成本函数:

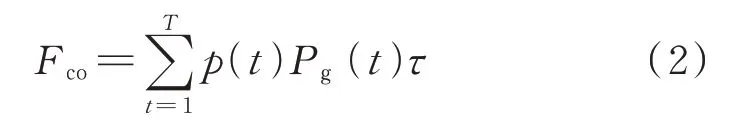
式中:p（t）为分时电价函数。Fco计算了用户次日用电费用,为价格型DR 目标函数。

最后,由线性加权法［27］定义综合考虑两种目标的联合目标函数。

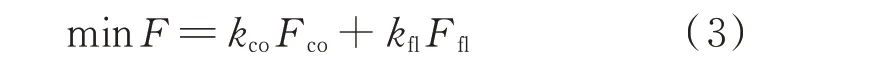
式中:kco和kfl分别为价格型和激励型DR 目标的权重系数,在签署合同时根据用户偏好确定。

值得说明的是,由于存在激励水平等模糊性因素和用户心理等随机性因素,在日前优化计算时ωDR的取值具有不确定性,即用户的响应行为是未知的。而售电公司支付的补贴价格应由实际达到的效果决定,用户的响应收益结算存在一定延迟。因此,在优化次日用电费用时不考虑用户参与激励响应的额外收益,而日后应将激励收益计入并评估当日的实际净收益。

设备约束参考附录A 式（A1）至式（A20）。此外,系统应满足功率平衡的全局约束式（A21）。

2 基于参数空间包络域期望的响应能力量化评估方法

2.1 考虑参与度不确定性的需求响应特性分析

居民用户响应行为的不确定性限制了激励型DR 业务实施的效果。本文将用户的激励型DR 参与度ωDR视作服从正态分布［22］的随机变量,以表征用户响应行为的不确定性,即ωDR～N(ωˉDR,δ2DR)。其中ωˉDR为用户的参与度均值,表示该用户参与激励型DR 的中心意向；δDR为用户的参与度标准差,反映了该用户响应行为的离散程度,其值越大则用户参与度“弹性”越大。

2.2 基于参数空间包络域期望的响应能力量化方法

目前需求响应能力评估方法通常忽略用户参与意愿的不确定性,或将不确定因素用置信区间与区间数表示［28］。本文考虑量化居民响应容量期望,用于评估指标的构建。所提计及居民用户意愿不确定性的响应容量期望υDR的计算如下。

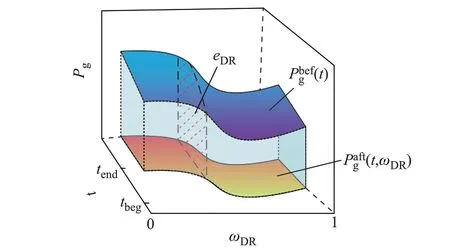
图1 考虑用户参与度差异的净负荷响应Fig.1 Response net load considering difference in customer participation degree

当用户受到外界其他不确定因素影响时,式（4）计算出的响应能力随之变化。若在评估时需要考虑光伏出力等新的不确定性因素时,可将新随机变量规范化到［0,1］区间内,类比对ωDR的处理推广到高维空间中的积分。

2.3 基于响应容量期望的响应能力梯度评估指标

对响应能力的评估不能仅局限于对响应容量等直观效果的评价,还应考虑付出的代价。电网对参与响应的用户需要支付相应的经济补偿成本；而用户参与响应的成本体现在调整用电行为的舒适度损失上。激励成本和响应效益的关系决定售电公司推行激励型DR 政策的力度,而响应成本与响应效益的关系决定用户参与激励型DR 的力度。因此,本文提出响应能力梯度评估指标,利用售电公司和用户付出单价得到的响应服务衡量响应边际效用。

2.3.1 单位激励成本下的响应能力梯度评估指标

用户响应容量期望υDR随激励成本CDR变化的特性曲线见附录A 图A2［29］。考虑构建单位激励成本下的用户响应能力指标υa,DR,反映激励型DR 机制对电网经济性和有效性的综合影响。

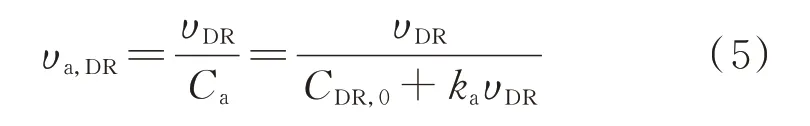
式中:Ca为售电公司支付的激励代价函数；CDR,0为用户参与响应的激励成本开启阈值,即固定收益；ka为单位期望响应容量增量下激励成本的对应增量,即激励系数。

2.3.2 单位响应成本下的响应能力梯度评估指标

居民用户中断和转移负荷将产生响应舒适度成本。考虑到一般用户边际响应成本递增,用二次函数［11］描述终端用户付出的响应代价函数Cu如下:

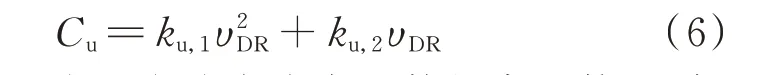
式中:ku,1和ku,2为用户响应成本函数的常系数,即舒适度系数。

与υa,DR类似,为评估单位响应成本下用户的响应能力,构建指标υu,DR:

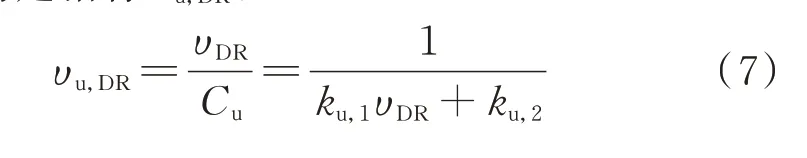
3 算例验证

SHEMS 算例中考虑的SA、IA 和BA 参数参考文献［8,30-31］设置,如附录A 表A1—表A3 所示。PV 功率预测所用原始数据集来源于美国马萨诸塞大学安姆斯特分校的Smart*计划,包含北美100 个户用PV 系统2015 年的实测功率和气象数据。采用的反向传播神经网络（BP-NN）超参数详见表A4。在PyCharm 平台编程,网络训练和测试结果如图A3所示。设置调度周期为次日00:00 到24:00。将一日分为48个时段,τ=0.5 h。分时电价见图A4［9］。优化算例仿真平台为MATLAB R2020a,从YALMIP工具箱调用GUROBI 优化求解器进行求解。

3.1 所提SHEMS 的合理性与有效性分析

为验证本文所提SHEMS 的合理性与有效性,将其与同样考虑用户侧负荷曲线优化DR 的文献［14-15］中的方法进行对比分析。首先模拟理想情况,假定用户全力参与DR,不考虑用户响应行为的不确定性,共设置4 个对比场景。1）基准场景（BC）:针对未安装SHEMS 的用户,其不具备优化能量消耗的能力,作为空白对照组；2）优化场景1（OC1）:SHEMS 利用文献［14］的方法优化用户次日能量消耗；3）优化场景2（OC2）:利用文献［15］的方法进行优化；4）优化场景3（OC3）:利用本文方法进行优化。测试集中某晴天4 个场景下的负荷最优调度结果和分析详见附录B 图B1 及相关说明。

在完整测试集下（包含20 日晴天数据）,上述4个场景的优化结果对比如附录B表B1所示。表中指标均为20 天的平均值,其中用电费用为正表示用户用电支出大于售电收益。由表B1 不难发现,无论从电网还是用户的角度考虑,OC3 的效益均最佳,而所需仿真用时则比OC1 和OC2 多37 s 左右,然而以上3 个场景的仿真时长均符合日前优化调度问题的要求［32］。因此,所提SHEMS 在用户完全响应的理想情况下表现出更好的综合性能,具有一定有效性。

与文献［14-15］不同的是,所提SHEMS 还考虑了非理想情况下的响应模型,即用户响应意愿的不确定性问题。式（3）所述用户偏好kco-kfl有3 种取值情形:0-1、1-0 和1-1,本节实验均考虑用户签署1-1合同,即同意参与价格型和激励型DR。在合同有效期内,用户可于日前自主决策次日的激励型DR参与度系数ωDR,从而充分调动终端用户参与DR 的积极性。而ωDR决定了净负荷曲线的优化效果（电网效益）和用户的响应成本与补贴收益。

1）ωDR对电网效益的影响。以时间、功率和参与度ωDR为轴构建三维空间坐标系,绘制响应前后净负荷功率曲面如图2（a）所示。图2（b）展示了日内净负荷功率最值随ωDR变化的情况,可以看出,随着ωDR的增大,DR 后的净负荷功率曲线逐渐向内收敛。说明随着用户参与度提升,全时段内的响应效果越来越好。利用光伏发电时段下用户消耗功率占光伏出力的比例计算光伏消纳水平,全天净负荷方差及光伏消纳水平随ωDR的变化如附录B 图B2 所示。可以看出,相较于ωDR≠0 时的所有优化结果,不参与激励型DR 的净负荷功率曲线波动较为剧烈,光伏消纳水平较低。而当用户参与激励型DR后,随着ωDR逐渐增大,全天净负荷方差呈指数衰减趋势,光伏消纳水平迅速上升后趋于平缓。

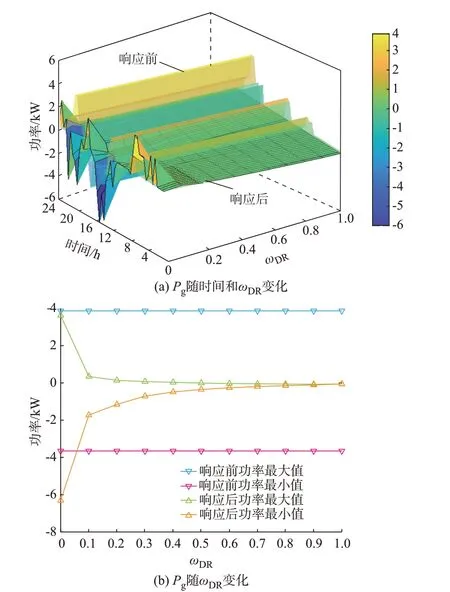
图2 需求响应前后净负荷功率随ωDR 和时间的变化规律Fig.2 Variation of net load power with ωDR and time before and after demand response

2）ωDR和激励水平对用户的影响。文献［33］将用户划分为经济型用户（EU）、标准型用户（SU）和舒适型用户（CU）,并指出可观测且能量化的用电偏好是经济型和舒适型偏好。鉴于此,本文研究具有显著特征的EU 和CU 两类用户,EU 对经济效益更敏感,舒适度系数较小；而CU 对舒适度损失更敏感,舒适度系数较大。

（1）EU:取舒适度系数ku,1=ku,2=1,激励固定收益CDR,0=0.5,研究激励系数ka的变化对用户成本-效益的影响。设Δka为ka的取值间隔,以Δka=2为梯度设置多组激励水平,对比实验得到ka在3 个区间内用户效益呈现不同的规律:ka＜6（图3（a））；ka=6（图3（b））；6 ＜ka＜18（图3（c））；ka≥18（图3（d））。图3 中经济净收益表示不计舒适度成本的用户收益与成本的差值,包括售电收益、激励补贴收益和购电成本；综合净收益则为经济净收益与舒适度成本的差值。图中绿色和蓝色虚线分别标记了经济净收益和综合净收益的变化趋势,红点标出了收益最大值。

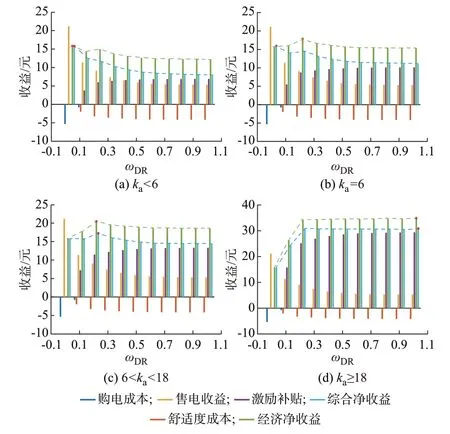
图3 EU 收益随激励和ωDR 的变化规律Fig.3 Variation of EU’s benefits with incentive and ωDR

从图3 不难发现,激励补贴收益和响应舒适度成本均随参与度增大而增大,增长速度由快到慢变化,而激励补贴收益则随ka增大而线性增长；用户的购电成本和售电收益均随参与度增大而减小。这说明,当售电公司设置合理的激励水平时,可以使得用户的激励收益增量在一定程度上补偿用户的售电收益减量和舒适成本增量,使得用户效益在某种参与度下达到最高。图3（a）显示用户的经济净收益和综合净收益均在ωDR=0 时达到最大,说明此时激励水平设置过低,将无法引导用户参与DR；图3（b）显示当激励水平增长到ka=6 时,用户的经济净收益在ωDR=0.2 处最优,而综合净收益仍在ωDR=0处最优,说明该激励水平下用户的售电收益减量补偿效果较好,而舒适成本增量则未得到有效补偿；图3（c）显示当激励水平设置较高时,用户经济净收益和综合净收益变化规律一致,均在ωDR=0.2 处达到最高,用户的售电收益减量和舒适成本增量都得到了有效补偿；而图3（d）则展示了激励水平过高时的过补偿现象,用户的两种净收益指标都随ωDR递增。由于图2 显示ωDR越大电网效益的增量越小,过补偿虽能提高用户参与度水平,但售电公司需支付的激励成本过高,电网效益提升却不明显,因此不建议设置过高的激励。此外,对于电网而言,由于EU对经济效益的敏感度更高,在设计激励水平时可以仅考虑EU 的经济净收益而节省激励成本,即选取ka=6 的方案。对于终端用户而言,在这种激励机制下SHEMS 可以为该EU 提供最优参与度建议,即ωDR=0.2。

（2）CU:取舒适度系数ku,1=ku,2=2,CDR,0=0.5,同EU 一样设置多组ka进行对比实验。与EU不同的是,由于CU 对舒适度更为敏感,售电公司在优选ka时应考虑用户的综合净收益,用较高的激励水平补偿用户的舒适度损失,即搜索规律与图3（c）一致的临界点。附录B 图B3 展示了该临界点下CU的成本-效益变化规律,此时ka=10,用户综合效益在ωDR=0.2 处达到最优。可见,由于CU 参与激励型DR 的舒适度成本较高,相较于EU 来说售电公司的ka优选值也较大,这与实际情况下的规律相一致:EU 出清价格较低而先被调用,CU 出清价格较高而后被调用。

由以上分析可知,所提SHEMS 通过设置自主决策参与度系数ωDR考虑了用户响应意愿的不确定性。分析所有可能的场景下电网效益与用户效益的变化规律,能够在电网与用户双方利益博弈中取得一个优胜的建议。因此,所提SHEMS 具有一定合理性与有效性。

3.2 所提响应能力评估指标的合理性与有效性分析

3.2.1 基于参数空间包络域期望的响应能力量化方法分析

考虑居民用户对激励合同响应行为的不确定性,假设用户参与度ωDR～N(ωˉDR,δ2DR)。为验证所提响应能力期望评估指标υDR的合理性与有效性,将其与文献［22］和［7］中所提响应潜力评估指标进行对比分析。文献［22］的可削减度指标st定义见附录B 式（B1）,为瞬时响应能力评估方法；文献［7］的可用电能灵活性（AEEF）指标sAEEF定义见式（B2）,为持续性响应能力评估方法。考虑到传统方法常用区间数模拟随机性特征,本节首先找出st和sAEEF所有可能的观测结果,分别如图4（a）、附录B 图B4（a）所示。为控制变量,所有指标均对图2 的优化结果进行评估。

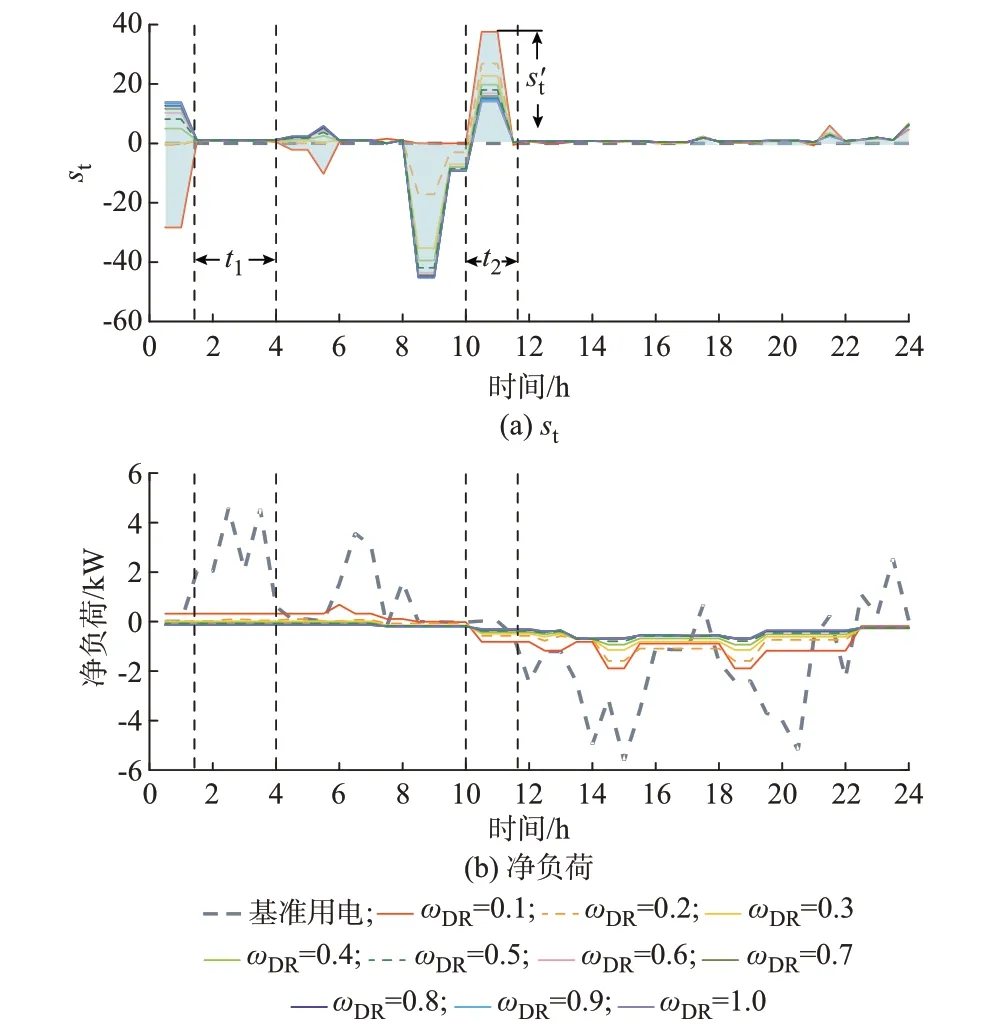
图4 st 和净负荷随时间变化规律Fig.4 Variation of st and net load power with time

图4（a）反映了用可削减度计算得到的居民用户瞬时响应潜力变化规律,st＞0 表示负荷削减潜力,反之表示负荷增加潜力。在每个时刻点上可以得到响应潜力的区间数s′t,在图中用浅绿色阴影表示。图4（b）则展示了次日实际达到的净负荷塑形效果。可以看出,当基准负荷Pbefg数值较大而响应后负荷Paftg数值较小时,st并不能反映负荷塑形的真实潜力,如图中标出的t1时段:st数值小,负荷实际削减能力却较大。显然,这是定义指标的附录B 式（B1）决定的。此外,即使在Pbefg与Paftg数值接近时,st也不能反映实际响应效果。如t2时段下st随ωDR增大而减小,而由图4（b）可知净负荷的实际波动抑制效果随ωDR增大而更优。由此可见,可削减度指标并不适用于对智能用户柔性负荷重塑能力进行评估。事实上,对于负荷转移或重塑类型的持续性DR 事件,在某时刻下的响应容量也不能代表整个响应周期内用户达到的响应效果,采用瞬时响应能力评估方法不具参考意义。

附录B 图B4（a）展示了居民用户的持续性响应潜力sAEEF随ωDR变化情况,其对应区间数为s′AEEF。可以看出,利用该指标评估的智能用户响应能力规律与图2 反映的实际情况一致。为验证所提υDR的有效性而进一步比较sAEEF与υDR。首先将响应电量归算为平均响应容量（AEPF）以统一两者的量纲,相应指标sAEPF和其区间数s′AEPF见图B4（b）。区间数表示了随机变量的值域范围,有s′AEPF=s′AEEFT。图B5 展示了s′AEPF和υDR随中心意向ωˉDR与参与度弹性δDR变化的规律,具体分析详见附录B。

综上所述,所提基于参数空间包络域期望的响应能力量化指标不仅能够从物理意义上有效量化智能用户的响应容量,还能对不确定性情景下不同分布特性用户的响应特征进行分析与综合,从而具有一定合理性与有效性。

3.2.2 基于响应容量期望的响应能力梯度评估指标分析

为验证所提单位激励成本下的用户响应能力梯度指标υa,DR、单位响应成本下的响应能力梯度指标υu,DR的有效性,设置105 种不同参与度分布（见附录B 图B6）的用户计算以上两种边际效益评估指标,说明其分别对于售电公司和终端用户的指导意义。

取ku,1=ku,2=2,CDR,0=0.5,ka=10。归一化后的υa,DR和υu,DR随ωˉDR与δDR变化的曲面分别如附录B 图B7（a）、（b）所示。可以看出,计及不同成本的两个指标随参与度参数的变化趋势呈镜像态,反映出售电公司与家庭用户两个群体目标意向的相互矛盾。观察图B7（a）可知,对于售电公司而言,边际效益指标υa,DR在ωˉDR最大、δDR最小时达到最大值,这个结论也反映了电网期望用户参与度中心意向较高且参与意愿的波动尽量小。这是因为,ωˉDR线性增大时期望响应容量υDR的增量指数型衰减,由于电网付出的激励成本随υDR线性增加,所以激励成本的增长态势逐渐趋于平缓。因此,售电公司可以付出不大的经济代价增量而获取更多的响应服务,即其边际效益递增。而由图B7（b）可知,用户单位响应成本下的响应效益则在ωˉDR最小、δDR最大时达到最大值,这是由于考虑到用户的边际成本递增特征,以二次函数折算的响应舒适度代价随ωˉDR增大而迅速增长,υu,DR则相应减小。值得注意的是,当ωˉDR较小时两种计及成本的响应能力评估指标与参与度弹性的关系是非线性的,分别在δDR=0.04 时取得最大值和最小值,如图5（a）、（b）中虚线标记所示。

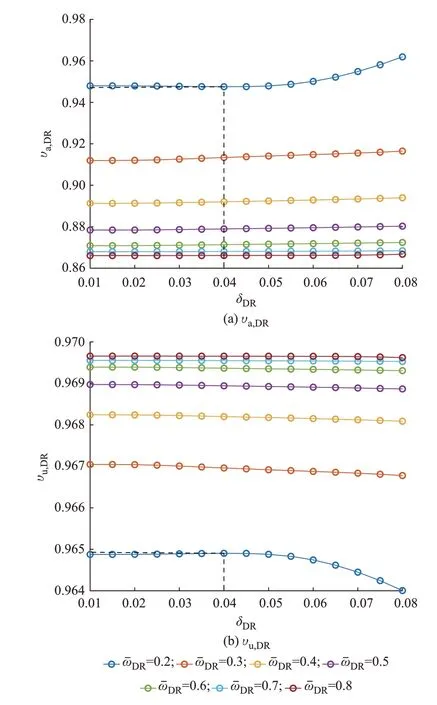
图5 不同ωˉDR 下υa,DR 和υu,DR 随δDR 变化规律Fig.5 Variation of υa,DR and υu,DR with different δDR and ωˉDR

图5 显示,在用户参与激励响应的平均水平偏低时,参与度弹性对响应能力梯度指标的贡献不是单调递增或递减的,适当的取值可以优化居民侧的响应能力。例如,电网往往期望用户在中心意向较低时离散程度更大,通过提高灵活性而提高电网可能的收益,而所提边际效益指标υa,DR则给出了这种场景下寻找最优灵活性用户的指导（在ωˉDR=0.2时,υa,DR在灵活性δDR=0.04 时达到最高）。因此,采用所提指标对用户不确定性响应行为分析可以为智能用电家庭参与DR 的行动方案提供决策依据,同时对售电公司激励机制的设计具有指导意义。

兼备高性能计算和数据处理技术的SHEMS 恰恰为居民用户提供了调整响应计划的智能规划平台。可以展望,未来的SHEMS 可由历史数据辨识出用户的响应行为习惯参数ωˉDR和δDR,通过误差控制等手段向最优参数逼近,然后综合考虑用户经济性和舒适度生成最佳推荐响应方案,达到优化用户响应能力的目的,使得激励型需求响应的评估与优化控制形成一个完整的闭环。

4 结语

SHEMS 的合理设计和评估能够提高居民侧参与需求响应的潜力,为源-网-荷协同互动技术提供有力支撑。本文建立了激励型需求响应的参与度自主决策优化调度模型,通过分析电网与用户效益随激励水平与参与度的变化规律,能够为售电公司针对不同类型用户设计激励机制提供指导,并为用户决策提供合理的建议。考虑到用户响应行为的不确定性,本文提出了基于参数空间包络域期望的需求响应能力量化方法,并基于此提出了考虑电网激励成本和用户响应成本的响应能力梯度评估指标,结合物理意义和多种不同参与度分布的家庭案例说明了其合理性与有效性。

本文工作还存在一定局限性,如尚未考虑数据预测误差对实际优化调度效果的影响、激励设计较为简单等。此外,所提评估方法的验证仅在仿真层面进行,真实响应数据的缺乏成为实际应用过程中可能面临的挑战。后续研究将从考虑多种不确定性因素、不同激励形式、结合有限历史数据对用户响应行为进行参数辨识和生成模拟等方面进一步开展。

本文研究得到国网浙江省电力有限公司科技项目“用户侧可调控资源聚合效能提升与网荷互动技术研究与应用”(5211DS20008J)的资助，特此致谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。