基于改进直流断路器注入信号的柔直电网自适应重合闸方案

2022-04-18张大海杨宇辰梁晨光刘艳梅和敬涵

电力系统自动化 2022年8期

张大海，杨宇辰，梁晨光，李猛，刘艳梅，和敬涵

（北京交通大学电气工程学院,北京市 100044）

0 引言

基于模块化多电平换流器（modular multilevel converter,MMC）的柔性直流输电技术具有控制灵活、无换相失败、输出电气量谐波含量低等优点,在新能源并网、连接弱交流系统等方面有着广阔的应用场景［1-2］。考虑到远距离、大容量输电的成本问题,柔性直流电网广泛采用架空线路进行功率传输［3-4］。然而架空线路长期暴露在大气中,发生瞬时性故障的概率较高。为了提高直流电网供电的可靠性,需要合理配置重合闸方案［5-6］。

目前,工程上通常采用自动重合闸方案实现故障恢复［7-8］。该方案无法在合闸操作之前判别故障性质,当断路器重合于永久性故障时,会对柔性直流电网中的电力电子设备造成二次冲击,严重危害直流系统的安全稳定运行。因此,亟须研究具备预先判别故障性质能力的自适应重合闸策略,避免直流断路器（direct current circuit breaker,DCCB）重合于永久性故障。

针对自动重合闸存在的问题,已有文献提出基于主动信号注入的自适应重合闸方案,主要分为以下两大类:

1）采用换流器注入信号的自适应重合闸方案。文献［9］通过调整换流器的控制策略,短时间内导通DCCB 的转移支路,向直流线路注入一个幅值较小的电压脉冲,检测电压反射波的极性来确定故障性质。文献［10］在换流器的控制策略中增加故障性质辨识模式,通过主动注入一定特征频率的电压信号来判别故障性质。文献［11］利用全桥型MMC 的高可控性,通过附加控制策略向故障线路注入电压方波信号,根据行波测距原理判别故障性质。以上方法应用于多端直流电网时,换流器控制策略的改变将引起直流电压的突变,从而影响非故障线路的正常运行,对相邻的健全线路造成扰动甚至冲击。

2）采用DCCB 或辅助装置注入信号的自适应重合闸方案。文献［12］通过投切级联全桥型DCCB的转移支路子模块,产生一定频率的检测电压,根据断路器端口电压、电流在对应频率下的相位特征判别故障性质。文献［13］在全桥型DCCB 中附加控制策略,短时间导通少量的子模块,向线路注入电压脉冲,通过行波测距判别故障性质。然而此类方法对于不同拓扑结构的混合式DCCB 不具有普适性。文献［14］对DCCB 的拓扑进行改进,增加辅助电路实现信号注入,检测电流反行波的极性判别故障性质。由于晶闸管的关断条件限制,该方法不能控制信号的注入次数,不利于判别持续时间较长的瞬时性故障。文献［15］利用断路器实现电气隔离,通过并联吸能电路注入脉冲信号,根据电压反行波的极性判别故障性质。但该方法无法调整注入信号的幅值,幅值过小将影响高阻接地故障的检测,幅值过大又可能会导致故障点再次击穿。

此外,限流电抗器对注入信号具有明显的衰减作用,而现有研究缺乏相关的理论分析与推导,容易导致自适应重合闸方案失效。

本文提出一种适用于混合式DCCB 的RCT（resistor-capacitor-thyristor）型缓冲电路,增加主动信号注入模式来实现自适应重合闸。该方案充分利用断路器的电气隔离作用,不影响多端直流电网功率传输的稳定性；在推导电抗器衰减作用的基础上选取注入信号脉宽,并基于行波保护信息自适应调整注入信号幅值,有效提高故障性质判别的可靠性与准确性。

1 一种RCT 型缓冲电路

1.1 混合式DCCB 拓扑结构

混合式DCCB 的拓扑结构如图1 所示,由主支路、转移支路以及耗能支路并联组成［16-17］。主支路由超快速机械开关（ultra fast disconnector,UFD）与负载换流开关（load commutation switch,LCS）串联而成；转移支路由绝缘栅双极型晶体管（insulated gate bipolar transistor,IGBT）共发射-集电极串联型子模块组成；耗能支路由金属氧化物电阻（metal oxide varistor,MOV）串并联构成。对于多端直流电网而言,若能充分利用断路器的电气隔离作用,控制DCCB 注入信号来判别故障性质,与基于换流器注入信号的自适应重合闸方案相比,可以避免信号产生过程对相邻健全线路的干扰、冲击。

图1 混合式DCCB 拓扑结构Fig.1 Topology of hybrid DCCB

由电阻、电容、二极管组成的传统RCD（resistor-capacitor-diode）型缓冲电路并联于IGBT两端,起到保护IGBT、协助换流的作用［18-19］。当转移支路处于导通状态时,缓冲电路两侧的电压为IGBT 的通态压降,近似等于0。一旦向IGBT 发送关断信号,短路电流快速换流至缓冲电路,通过二极管D 对电容C充电。该充电过程可以限制IGBT 两端电压的上升率,减小由关断信号延时导致的动态压差,抑制尖峰电压。随着MOV 两侧的电压上升至启动阈值,耗能支路导通并泄放直流系统储存的能量。能量泄放完毕后,故障电流被DCCB 阻断,各电容两端的电压之和与断路器两侧的电压相等,电阻Rp用于减小由IGBT 漏电流不一致引起的静态压差。当转移支路再次导通时,电容C经电阻Rs释放能量,端电压下降至0。

由上述换流过程可知,在DCCB 阻断故障电流至再次导通转移支路的时间内,电容C中储存的能量没有被释放。以此为突破口,本文对传统的RCD型缓冲电路进行改进,在不影响其正常缓冲、换流能力的基础上,增加主动信号注入模式,将储存在电容C中的能量注入线路,旨在判别故障性质。

1.2 RCT 型缓冲电路工作模式

本文提出一种RCT 型缓冲电路,其拓扑结构与工作模式如图2 所示,图中红色为电流流通路径。

图2 RCT 型缓冲电路拓扑结构与工作模式Fig.2 Topology and working modes of RCT snubber circuit

该缓冲电路由电阻、电容、晶闸管构成,并联于转移支路的IGBT 共发射-集电极串联型子模块两侧。由于混合式DCCB 具有双向开断故障电流的能力,晶闸管T1、T2反向并联,双向电流均可通过晶闸管对电容C充电。基于缓冲电路中晶闸管、子模块中IGBT 的可控性,可实现脉冲信号注入。

本文所提RCT 型缓冲电路具有以下2 种工作模式:

1）缓冲、换流模式。以开断正向故障电流为例进行说明,反向断流情况与之类似。当转移支路流过正向故障电流时,向晶闸管T1施加触发脉冲,并向IGBT 发送关断信号。T1的触发脉冲先于IGBT关断信号150 μs 施加,在发送关断信号150 μs 后移除,以保证可靠缓冲、换流。晶闸管T1承受正向电压而导通,晶闸管T2保持关断状态。此时换流通路如图2（a）所示,电流通过晶闸管T1对电容C充电,实现动态均压。随着故障电流换流至耗能支路,晶闸管T1承受反向电压自行关断。由于晶闸管的钳位作用,各电容两端的电压之和为DCCB 两侧的峰值电压。电阻Rp、Rs共同实现IGBT 的静态均压,且Rp的阻值远大于Rs。因此,电容C无法经电阻Rp放电,而是始终通过电阻Rs缓慢释放能量。

2）主动信号注入模式。首先将配置RCT 型缓冲电路的子模块划分为:电容放电（Ⅰ类）子模块、非电容放电（Ⅱ类）子模块。在DCCB 阻断故障电流后,断开残余直流电流断路器K1,实现电气隔离［20］。经过大约300 ms 的去游离,闭合快速机械开关K2。向Ⅰ类子模块中的晶闸管T2施加触发脉冲,并短时间导通Ⅱ类子模块中的IGBT g2。此时放电通路如图2（b）所示,实现向故障线路注入一个幅值为负的电压脉冲。通过改变Ⅰ类子模块投入的数量,可调整注入脉冲信号的幅值；控制Ⅱ类子模块的g2导通时间,即可调节电压脉冲的宽度。

如附录A 图A1、A2 所示,转移支路分别采用全桥结构、二极管桥式结构的子模块时,RCT 型缓冲电路均能实现以上2 种工作模式,在不同拓扑结构的混合式DCCB 中具有普适性。

1.3 RCT 型缓冲电路参数设计

结合实际工程情况,混合式DCCB 的转移支路由多级子模块串联而成,假设每级子模块两侧均并联有RCT 型缓冲电路。当IGBT g1先于其余串联IGBT Δtoff时间关断时,流经g1的电流立即向电容C换流,由于电容C两端的电压无法突变,g1两侧的电压Ug1将缓慢上升,满足:

由式（2）可知,增大电容C的取值,可以减小最大电压差ΔU,增强动态均压的效果。但电容C的取值过大,会延长缓冲电路的换流过程,进而增加DCCB 隔离故障所需的时间。综合考虑动态均压和快速断流的需求,电容C选取为207 μF。

在大约300 ms 的去游离时间内［10］,电容C通过电阻Rs缓慢放电,端电压按指数规律下降。Rs的取值需确保注入信号时电容C两侧电压的幅值足够大。本文设经去游离时间放电后,电容C两端电压为初始值的80%,则电阻Rs需要满足:

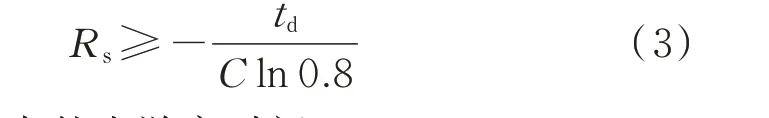
式中:td为故障点的去游离时间。

根据式（3）,将电阻Rs选取为6.5 kΩ。在RCT型缓冲电路中,电阻Rp、Rs共同实现IGBT 的静态均压。通常取Rp、Rs的总电阻为IGBT 关断电阻Roff的1/10［22］,即可确定电阻Rp为2.3 MΩ。

2 注入信号特征的选取与调整

向不同故障状态下的直流线路注入电压脉冲,在线路首端检测到的电压波极性具有明显差异,以此判别故障性质较为简单直接,文献［9-15］均采用该方法进行故障识别。但已有文献未计及限流电抗器对电压脉冲的衰减作用,且注入固定幅值的信号势必存在耐受过渡电阻的问题。

2.1 注入信号宽度的选取

由式（4）、式（5）可解析得到放电系数γ与脉宽Ton的对应关系,与仿真值对比如附录A 图A4 所示。随着Ton的增加,电容C持续释放储存的电能,导致端电压uC下降。当Ton不超过500 μs 时,uC不低于0.84 倍的初始值,即信号注入期间,电容C两侧电压的下降程度较小。

故假设电容C的端电压uC在Ton内保持初始值UC不变,进一步研究电抗器对注入电压脉冲的衰减作用。信号注入线路的等效电路如附录A 图A5示。在复频域,NCUC/s、NC/(sC)分别为NC个子模块的等效电压与等效容抗,u1q(s)为线路首端的电压行波,ZC为线路的波阻抗。求解等效电路,可以得到电压行波u1q(s)的表达式为:

根据式（8）、式（9）,解析得到衰减系数α与脉宽Ton的对应关系,与仿真值对比如附录A 图A6 所示。Ton≤300 μs 时,α随Ton的增加而增大；当300 μs ＜Ton≤500 μs 时,α基本保持不变。因此,为了减小电抗器的衰减作用,应适当增加Ton。但近距离故障下,Ton过大会导致反射波首端与前行波末端重合,在一定程度上影响电压波的检测效果。综合考虑以上因素,将脉宽Ton选取为100 μs,对应的衰减系数α=0.35。同时,将晶闸管T2的触发信号宽度选取为300 μs,先于IGBT g2的触发脉冲100 μs 施加,保证可靠注入信号。

2.2 注入信号幅值的自适应调整

根据1.2 节的分析,在晶闸管T1承受反向电压自行关断后,N个电容C两侧的电压总和为DCCB两端的峰值电压Ubmax。电容C始终经电阻Rs缓慢放电,在t时刻注入电压脉冲的幅值up为:

式中:Krel为可靠系数,考虑实际存在的各种误差影响,取Krel=0.85；α为电抗器的衰减系数,脉宽Ton=100 μs 时,α=0.35；Kline为线路的损耗系数,通过仿真可得Kline=0.49。

由式（12）可知,针对高阻故障场景,需要注入幅值较大的信号。但注入电压脉冲的幅值过大,在发生金属性短路且线路绝缘强度未充分恢复的情况下,会导致故障点再次发生击穿［23］。为此,本文利用行波保护信息预估过渡电阻,提出注入信号幅值的自适应调整策略。

文献［24-25］提出的直流线路行波保护方案分别将电压变化率（du/dt）、极波变化率（dP/dt）作为判据量,与电压变化率相比,极波变化率受线路的衰减影响较小。在线路全长240 km 范围内,设置经0 Ω 至600 Ω 过渡电阻接地故障,行波保护根据线路首端的电气量信息,计算得到极波变化率幅值（dP/dt）max的变化见图3。由图3 可知,（dP/dt）max能反映Rf的大小,当故障距离一定时,（dP/dt）max随Rf的增大而降低。因此,考虑选取整定值（dP/dt）set,通过比较（dP/dt）max与（dP/dt）set的大小对过渡电阻Rf进行预估。结合式（11）可计算得到故障点的反射系数βf。将βf代入式（12）,确定所需注入电压脉冲的幅值up。通过式（10）调控Ⅰ类子模块投入的数量,可以实现注入信号幅值的自适应调整。

图3 极波变化率幅值变化Fig.3 Amplitude variation of polarity wave change rate

设距离线路首端x=lkm 处发生经0 Ω 至600 Ω过渡电阻接地故障,通过行波保护计算得到一系列的极波变化率幅值,记作（dP/dt）max,x=l。由图3 可知,故障距离x的增加会使（dP/dt）max发生一定程度的衰减,对于x＜lkm 与x＞lkm 处的故障,满足:

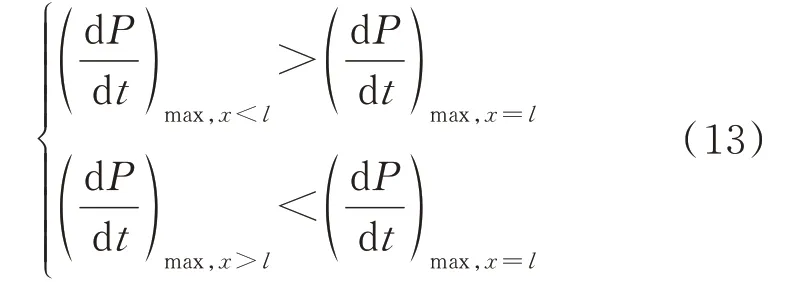
若将（dP/dt）max,x=l作为整定值（dP/dt）set,对于x＜lkm 处的故障,预估的过渡电阻Rf偏小,进而导致信号幅值up的计算值偏小；反之,x＞lkm 时,将造成up的计算值偏大。注入幅值偏小的信号,在高阻情况下可能导致故障性质的误判；而注入信号的幅值偏大,保证了故障判别的准确性。因此,将（dP/dt）max,x=0作为整定值（dP/dt）set。故障发生后,行波保护装置实时计算（dP/dt）max。待信号注入阶段,将（dP/dt）max与整定值（dP/dt）set作比较,判断（dP/dt）max所在的区间,自适应调整注入信号的幅值,如附录A 表A1 所示。

3 自适应重合闸方案

3.1 故障性质判别

在确定电压脉冲的宽度并自适应调整信号的幅值后,控制混合式DCCB 注入信号（负极性）。信号注入与行波传播特性如附录A 图A7 所示［15］,线路首端产生的电压行波为u1q,u1q沿着直流线路向前传播。在故障点处或线路边界处,波阻抗发生改变,电压行波在波阻抗变化的位置产生反射。

由2.2 节分析可知,发生永久性故障时,检测到极性为正的电压波um1。对于瞬时性故障而言,信号注入时,故障点的电弧已经消失,此时,电压行波u1q传播至n点发生反射。反射波u1f、反射系数βn为:

式中:Z1、Z2分别为反射点前、后的波阻抗。由于断路器CB21处于断开状态,线路末端可视为开路,即波阻抗Z2=∞。

根据式（14）可知,反射波u1f的极性与电压行波u1q的极性相同,即发生瞬时性故障时,测量点检测到的电压波um1极性为负。因此,通过比较um1的极性可以判别故障的性质。将幅值作为um1的观测量［9］,考虑一定的裕度,得到永久性故障判据为:

式中:uMM1为电压波um1的幅值。为了消除电压波动、噪声干扰等影响,uset设置为5 kV。

3.2 重合闸方案实现流程

本文提出的基于改进DCCB 注入信号的自适应重合闸方案动作时序如图4 所示。

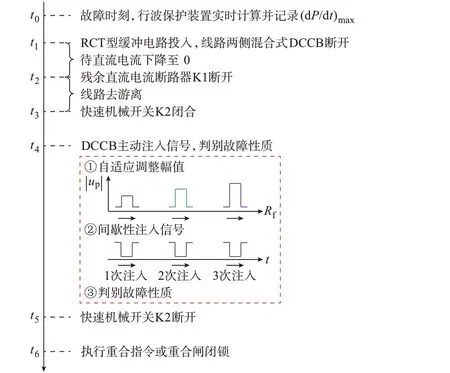
图4 自适应重合闸方案动作时序Fig.4 Operation sequence of adaptive reclosing scheme

1）假设t0时刻线路发生故障,行波保护装置实时计算并记录极波变化率幅值（dP/dt）max。

2）线路保护经短暂延时后动作,t1时刻RCT 型缓冲电路投入,线路两侧混合式DCCB 断开。

3）等待直流电流下降至0,t2时刻残余直流电流断路器K1 断开,实现电气隔离。

4）经过300 ms 左右的去游离后,t3时刻快速机械开关K2 闭合。

5）t4时刻混合式DCCB 主动控制,注入电压脉冲,判别故障性质,具体流程如图5 所示。

图5 故障性质判别流程Fig.5 Fault nature identification process

查附录A 表A1 判断（dP/dt）max所在的区间,自适应调整脉冲信号的幅值up。采用间歇性注入信号的方式,避免将持续时间较长的瞬时性故障误判为永久性故障。设定注入信号的次数nset=3,若检测到电压波幅值uMM1≥uset,且注入信号的次数ns小于设定次数nset,延时50 ms 再次注入信号；若第ns（ns≤3）次注入信号后,检测到uMM1＜uset,则判别为瞬时性故障；若注入信号的次数ns≥nset时,仍满足uMM1≥uset,则判定为永久性故障。

为确保每次注入信号的幅值足够大,在第2、3 次注入信号时需要通过式（10）修正Ⅰ类子模块投入的数量,并替换为未投入过的Ⅱ类子模块。考虑极端情况进行定量分析,线路末端发生经600 Ω 过渡电阻接地故障时,3 次注入信号需投入的Ⅰ类子模块数分别为53、55、57,而转移支路的子模块总数为300 级,具有较高的冗余度与充裕性。

6）t5时刻快速机械开关K2 断开。

7）t6时刻DCCB 执行重合指令或重合闸闭锁。

本文所提自适应重合闸方案利用断路器实现电气隔离,避免信号注入过程对多端直流电网功率稳定传输的影响。自适应调整信号幅值、间歇性注入信号提高了故障性质判别方法的准确性。

4 仿真验证

4.1 仿真建模

为了验证所提RCT 型缓冲电路与自适应重合闸方案的有效性,在PSCAD/EMTDC 中建立如附录B 图B1 所示的四端柔性直流输电系统仿真模型。

直流电网系统参数、混合式DCCB 及缓冲电路参数分别如附录C 表C1、C2 所示。换流器MMC1至MMC4均为对称双极结构,由半桥型子模块构成。MMC2采用定电压控制,其余换流器为定功率控制。架空线路采用如附录B 图B2 所示的频率相关模型,每2 个换流站之间的线路长度设置为240 km。

4.2 RCT 型缓冲电路仿真验证

4.2.1 缓冲、换流模式

为了验证缓冲、换流模式的有效性,考虑到IGBT 实际存在的关断延时差异,采样频率选取为200 kHz。当t=0.503 s 时,向转移支路的IGBT 发送关断信号,设置IGBT g1先于其余串联IGBT 5 μs关断。对子模块不含有缓冲电路以及两端并联有RCT 型缓冲电路两种情况进行对比仿真,结果如附录B 图B3 所示。图B3 中,Ug1为g1两侧的电压,Ug2为其余各同向串联IGBT 两端的电压,ΔU为Ug1与Ug2的差值。当子模块不含有缓冲电路时,g1关断后两侧的电压Ug1迅速上升,导致短时过电压。经过5 μs 延时,其余IGBT 同时断开,Ug1恢复至正常关断电压。关断过程中,电压差ΔU的最大值为7.89 kV。当子模块两端并联有RCT 型缓冲电路时,g1关断后Ug1的上升速度减缓,且与其余IGBT 关断后Ug2的上升速度保持一致。关断过程中,电压差ΔU不超过0.09 kV。因此,本文所提RCT 型缓冲电路可以限制IGBT 两侧电压的上升速度,减小关断过程中产生的电压差,有效抑制过电压。

4.2.2 主动信号注入模式

对主动信号注入模式进行仿真验证时,选取的采样频率为50 kHz。若所需注入脉冲信号的幅值为-39.72 kV,由式（10）计算可得Ⅰ类子模块投入的数量NC=19,在0.801 4 s 控制混合式DCCB 向线路注入一个脉宽为100 μs 的电压脉冲。在限流电抗器L的不同取值下,注入信号的仿真波形如附录B 图B4 所示。

由于误差的存在,实际注入的电压脉冲幅值为-39.17 kV。经50 mH 的电抗器衰减后,电压行波u1q的幅值为-13.6 kV。计算可得衰减系数α=0.35,在2.1 节中解析的结果与仿真结果一致,能够准确反映限流电抗器的衰减作用,同时验证了所提RCT 型缓冲电路主动注入信号的有效性。

注入信号的衰减程度与电抗器L的大小成正比,当L增大至150 mH 时,衰减系数α减小至0.2。结合式（10）、式（12）可知,极端情况下单次注入信号需要投入的Ⅰ类子模块数最大为100 级。若L进一步增大,可能导致3 次注入信号所需投入的Ⅰ类子模块总数超出转移支路的子模块数。此时,增大单次注入信号的幅值以满足故障判别的要求,但会造成注入信号的次数有所减少,可能在一定程度上延长瞬时性故障的判别时间。

4.3 自适应重合闸方案验证

在附录B 图B1 中正极线路OHL12P上设置不同类型的故障,F1为单极接地故障,F2为双极短路故障。电压波的测量点在线路OHL12P首端（m点）,采样频率选取为50 kHz。

4.3.1 瞬时性故障

当t=0.5 s 时,线路OHL12P中点发生瞬时性单极接地故障（金属性短路）F1,故障持续时间tf分别设置为0.3、0.35、0.4 s。通过行波保护计算所得（dP/dt）max为2.62×107kV/s,查附录A 表A1 确定注入信号的幅值up为-28.43 kV。间歇性注入信号后进行故障性质判别,仿真结果如附录B 图B5所示。

根据附录B 图B5（a）可知,由于瞬时性故障的持续时间为0.3 s,在0.801 4 s 注入电压脉冲时,故障点已经消失,线路首端产生的电压行波u1q传播至末端发生反射。m点检测到的第1 个电压波um1极性为负,满足uMM1＜5 kV,因此判别为瞬时性故障。对于图B5（b）、（c）所示持续时间较长的瞬时性故障,分别在第2、3 次注入信号后,检测到uMM1＜5 kV,同样可以准确判别故障性质。线路OHL12P中点发生瞬时性双极短路故障（金属性短路）F2,仿真结果如附录B 图B6 所示,判别过程与单极故障类似,这里不再赘述。判别出系统发生瞬时性故障后,DCCB 执行重合指令。

通过以上仿真分析,验证了所提方案对于检测持续时间较长的瞬时性故障具有优势,可以避免直流系统不必要的停运,提高供电恢复效率。

4.3.2 永久性故障

当t=0.5 s 时,线路OHL12P中点发生F1永久性单极接地故障,故障持续时间tf设置为10 s,过渡电阻Rf分别设置为0、300、600 Ω。通过行波保护计算所得（dP/dt）max分别为2.62×107、9.18×106、5.57×106kV/s,查附录A 表A1 确定注入信号的幅值up分别为-28.43、-62.27、-84.86 kV。间歇性注入信号后判别故障性质,仿真结果如附录B 图B7所示。

由附录B 图B7 可知,对于永久性故障而言,在每次注入脉冲信号时,电压行波u1q均传播至故障点发生反射。m点检测到的第1 个电压波um1始终为正极性,在第3 次注入信号后,仍满足uMM1＞5 kV,因此可判别为永久性故障。当线路OHL12P中点发生永久性双极短路故障F2时,仿真结果如图B8 所示,判别过程与单极故障类似,在此不再赘述。当判断出系统发生永久性故障后,重合闸闭锁。

为了进一步验证所提自适应重合闸方案的普适性,本文仿真了距离线路首端15、20、30、110、210 km 处,分别经300、600 Ω 过渡电阻的永久性单极接地故障,判别结果如表1 所示。

表1 永久性单极接地故障判别结果Table 1 Identification results of permanent pole-toground faults

由表1 中结果可知,在不同距离处发生永久性单极接地故障,过渡电阻分别为300、600 Ω 时,所提方案均能准确判别故障性质,具有较强的耐受过渡电阻能力。当故障距离小于15 km 时,受到脉冲宽度的限制,反射波与注入信号产生混叠。以DCCB完成信号注入为起始检测时刻,避免注入信号叠加于反射波上引起误判。近端故障判别结果如附录B图B9 所示,由于采样频率有限,所提方案存在一定的检测盲区（故障距离小于2 km）。将自动重合闸作为后备方案［7］,当检测盲区发生永久性故障并进行误合闸操作时,保护装置将再次检测到故障,混合式DCCB 快速分闸。

4.3.3 对系统健全部分的影响

附录B 图B10、B11 分别为永久性、瞬时性故障情况下,自适应重合闸过程中直流系统各电气量的变化情况。由图可知,断路器隔离故障后,故障线路传输的功率转移至健全线路。在DCCB 主动注入信号、判别故障性质的过程中,健全线路的电压、电流以及各换流站输出的功率保持稳定,直流系统健全部分的正常运行不受影响。当判别为瞬时性故障时,断路器重合,故障线路逐渐恢复功率传输。

4.4 方案对比

4.4.1 技术指标对比

文献已有的自适应重合闸方案［9-15］根据信号注入源的不同可分为2 类:1）基于MMC 注入信号的方案；2）基于混合式DCCB 或辅助装置注入信号的方案。第1 类方案对于MMC 的拓扑结构和控制策略有特定要求,还会影响多端直流电网功率的稳定传输,因此仅适用于双端直流系统。第2 类方案利用断路器实现电气隔离,不影响相邻健全线路的正常运行,适用于多端直流电网,但依赖于混合式DCCB 的拓扑结构,或存在无法调控注入信号幅值、次数的问题。本文在第2 类方案的基础上进一步改进,提出的自适应重合闸方案较好地解决了以上问题,具有明显的技术优势。所提方案与已有方案技术指标对比如附录C 表C3 所示。

4.4.2 经济性对比

DCCB 转移支路的子模块主要分为反串联结构、全桥结构与二极管桥式结构,在相同的工况下,转移支路采用二极管桥式结构的子模块具有更低的成本［17］。因此,本节将RCT 型缓冲电路应用于二极管桥式结构子模块,在此基础上进行经济性对比。由3.2 节的定量分析可知,前文在RCT 型缓冲电路的配置数量上保留了较大的冗余度与充裕性。从经济性角度考虑,只需在165 级子模块两端配置RCT型缓冲电路,其余子模块配置传统的RCD 型缓冲电路,即可满足各类故障判别的要求。如附录B 图B12 所示,RCT 与RCD 型缓冲电路应用于二极管桥式结构子模块时,通过对Ⅰ类、Ⅱ类子模块进行调控,可实现缓冲、换流与主动信号注入。

混合式DCCB 的经济性由转移支路的开关器件数量决定,选取的IGBT、晶闸管与二极管额定参数均为4.5 kV/3 kA,单价分别为3.5、0.7、0.35 万元［26］。在±500 kV 直流系统的应用场景下,转移支路大约需要300 级子模块串联、5 条支路并联［5,7］。将二极管桥式拓扑、文献［12-14］采用拓扑以及本文提出拓扑所需主要器件数量汇总于附录C表C4。

文献［12-13］采用的转移支路子模块为全桥结构,若选取相同规格的IGBT,其关断电流的能力是二极管桥式拓扑的2 倍。因此,将文献［12-13］拓扑所需IGBT 数量等效为实际数量的一半。由附录C表C4 可知,本文所提拓扑的经济性优于文献［12-13］拓扑,与二极管桥式拓扑相比,成本提高了2.2%（173 万元）。文献［14］在二极管桥式结构的基础上增加了10%串联子模块数量的晶闸管,其注入信号的幅值远低于本文所提方案,且无法灵活调整信号幅值和注入次数。若降低对注入信号幅值、次数的要求,本文所提方案需要配置RCT 型缓冲电路的数量可进一步减少,成本将进一步降低。

由此可见,本文所提方案在满足各项技术指标的同时,不会大幅度增加成本,具有较高的灵活性,有利于技术指标与经济性需求的权衡。