基于连续近似线性规划的含UPFC 风电系统校正控制决策方法

周海强，顾婷艳，薛 峰，颜云松，宋晓芳

（1. 河海大学能源与电气学院,江苏省 南京市 211100；2. 国电南瑞科技股份有限公司,江苏省 南京市 211106）

0 引言

校正控制是系统安全稳定控制的重要环节［1］。由于电力系统中存在新能源及负荷波动、线路故障等不确定因素,故常出现静态电压或频率偏差过大、线路过载等静态不安全现象,如果不及时采取适当的校正控制措施,将有可能导致低频低压减载、新能源切机等严重后果,威胁电力系统安全。因此,制定合理的校正控制策略对于确保电力系统安全稳定运行非常重要。

风电对于中国能源转型发挥着重要作用,近年来,风电占比不断提高,截至2020 年底,中国风电累计装机容量已达281 GW［2］,但由于其具有随机性、波动性和间歇性,高比例风电的接入也使得电力系统的不确定性增强,在此条件下,如何对新型电力系统进行校正控制决策是一个亟待解决的问题［3］。

校正控制问题从数学上可以描述为安全约束的最优潮流问题（security constrained optimal power flow,SCOPF）,国内外学者对此进行了大量研究［4-6］。文献［7］通过调节统一潮流控制器（unified power flow controller,UPFC）来消除断线故障后的线路过载现象,应用灵敏度方法将校正控制问题转化为线性规划问题迭代求解,但研究限于确定性系统。文献［8］基于负荷节点电压和短路电流的综合灵敏度分析提出了一种电压校正控制方法。文献［9］研究了直流闭锁故障后受端系统的频率及电压安全校正控制问题。文献［10］考虑发电机有功功率调整速度的限制,提出一种计及过载线路发热严重程度的校正控制方法。文献［11］提出了一种计及柔性交流输电系统（FACTS）元件的事故后潮流快速校正控制模型。

对于不确定性电力系统,文献［12］基于广义负荷裕度提出了一种考虑负荷随机特性的静态安全校正控制方法。文献［13］应用场景法研究了风电系统的静态电压校正控制问题。文献［14］考虑了新能源预测误差,应用机会约束最优潮流（chance constrained optimal power flow,CCOPF）研究了基于移相器以及高压直流功率调制的校正控制策略。文献［15］应用分布鲁棒优化理论研究了考虑风电波动的电力系统静态安全校正控制问题。

综上,现有校正控制决策方法还存在以下不足:1）考虑的静态安全问题不够全面,已有工作常采用直流潮流,将潮流计算简化为线性问题,该方法可有效分析线路过载问题,但无法考虑静态电压和频率安全问题,而对于高比例新能源电力系统,频率及电压安全问题不容忽视；2）对于非线性不确定系统的校正控制问题缺乏高效率求解方法,已有方法主要有场景法［16］、机会约束规划（chance constrained programming,CCP）方法等,场景法计算量较大,且场景的代表性难以保证。CCP 方法主要应用于线性系统,对于非线性不确定系统则缺乏系统化求解方法；3）对UPFC、移相器等新型校正控制措施研究较少,传统控制措施代价较高且用户体验差,新型FACTS 装置可快速、灵活地调节节点电压、线路阻抗及系统潮流分布,具有传统控制措施所不具备的优点。

为此,本文针对含UPFC 风电系统,提出了一种基于连续近似线性规划（successive approximated linear programming,SALP）的校正控制决策方法,较好地解决了非线性不确定系统的校正控制问题。首先,对含UPFC 系统的潮流解耦计算方法进行了分析；接着,以控制代价为目标,建立了考虑风电及负荷预测误差的校正控制CCP 问题数学模型；然后,给出了基于灵敏度的SALP 求解方法；最后,以修改后的IEEE 10 机39 节点系统为例仿真验证了该方法的有效性。

1 含UPFC 的电力系统潮流计算

1.1 UPFC 的工作原理

UPFC 包括2 个背靠背连接的电压源型换流器（VSC）,一个VSC 通过变压器与交流系统串联,另一个VSC 通过变压器和交流系统并联。串联VSC可向系统注入有功功率和无功功率,从而控制串联支路潮流。并联VSC 可以发出和吸收无功功率,从而控制交流系统的节点电压幅值。

含UPFC 的输电线路等值电路如图1 所示。其中:节点l为并联VSC 连接节点；I˙t和I˙q分别为并联VSC 所抽取的有功和无功电流分量；V˙se为串联电压；rlm、xlm、blm分别为线路l-m的电阻、电抗和电纳；V˙l和V˙m分别为节点l和m的电压；Plm和Qlm分别为节点l向节点m流过的有功和无功功率；I˙2为串联VSC 上流过的电流；I˙z为线路阻抗上流过的电流。为简化分析,一般不计串联变压器等值电抗。

图1 含UPFC 的输电线路等值电路Fig.1 Equivalent circuit of transmission line with UPFC

UPFC 通过调节串联和并联电压V˙se和V˙sh将V˙l及Plm+jQlm控制为目标值,若Plm+jQlm设定值为Pc+jQc,则推导可知［17］:

式中:Zsh为并联变压器等值阻抗；上标“*”表示相量的共轭。

在此基础上,可进一步根据式（4）和式（5）计算串联和并联换流器容量Sse和Ssh。

1.2 含UPFC 系统潮流解耦计算

在计算含UPFC 系统潮流时,可将线路l-m断开,将m节点视作PQ节点,而将l节点视为受控的PV节点,其功率Plm与Vm之间满足式（1）。这样,计算潮流时只需对系统导纳矩阵作相应修改,并将雅可比矩阵中元素(∂Plm/∂Vm)Vm修改为［18］:

式（7）为系统有功和无功功率平衡方程。需要说明的是,传统潮流计算一般不考虑频率变化,但对于风电穿透率较高的系统,其频率波动不容忽视,故本文采用了计及频率变化的增广潮流来分析系统状态,文献［19］对此做了详细说明,此处不再赘述。

记UPFC 状态量Xupfc=[Vse,θse,Vsh,θsh],其中,θse和θsh分别为V˙se和V˙sh的相角；其边界参量Ybnd=[Vm,θm,θl,Plm,Qlm],其中,θm和θl分别为V˙m和V˙l的相角；Ybnd可由系统潮流解Xsys算出,设两者满足如下关系:

将式（1）—式（5）所描述的UPFC 静态模型简写为:

对于给定的控制参量usys和uupfc,根据式（7）可求出系统状态变量Xsys,再根据式（8）求出UPFC 的边界参量Ybnd,然后,在此基础上由式（9）求出UPFC 状态变量Xupfc,至此,可以完成含UPFC 系统潮流计算,确定系统及UPFC 稳态运行点。

2 含UPFC 的风电系统校正控制优化问题

在计及风速及负荷预测误差的条件下,含UPFC 的风电系统校正控制优化问题可描述为如式（10）所示的CCP 问题。

式中:目标函数F为校正控制总代价；cu和cd分别为发电机增、减出力的报价；P～L为负荷预测值；cL为切负荷代价系数；αv、αf、αline、αu为阈值。

约束条件包括式（7）—式（9）所描述的含UPFC系统潮流方程,以及关于发电机功率、节点电压、系统频率及线路传输容量的约束,其中:PW和PL分别为风电及负荷功率；Pg,max和Pg,min分别为发电机出力Pg的上、下限；Ru,max和Rd,max分别为发电机有功功率向上及向下调节速率的极限；Δt为校正控制有效时间,一般可取15 min；ρmax为最大切负荷率；Vˉ和-V分别为电压V的上、下限；fd,max和fd,min分别为频率偏差的最大值和最小值,本文分别取0.2 Hz 和-0.2 Hz；Sˉline和-Sline分别为线路传输容量Sline的上、下限。约束条件中还包括对UPFC 串并联电压及容量的约束,其中:Vˉse和-Vse分别为UPFC 串联电压的最大值和最小值；Vˉsh和-Vsh分别为并联电压的最大值和最小值；Sˉse和Sˉsh分别为UPFC 串联及并联换流器的容量Sse和Ssh的最大值；Pr {·}表示求概率函数。

考虑到PW和PL具有不确定性,因此系统潮流也具有不确定性。为了确保电力系统的静态安全性,式（10）中要求校正控制后节点电压、系统频率及线路传输容量位于安全区间内的置信度分别大于等于1-αf、1-αv和1-αline。另外,为了保证UPFC安全运行,校正控制时要求Vse、Vsh、Sse及Ssh位于安全区间内的置信度大于等于1-αu。

由于潮流方程及UPFC 的数学模型具有非线性,故式（10）描述的为非线性不确定系统CCP 问题。对于线性系统,其求解方法相对成熟,但非线性不确定系统CCP 问题的求解仍然是优化理论的难题［20］。粒子群优化等启发式方法计算量过大,算法收敛慢,很难付诸实施。为此,本文提出了一种基于SALP 的决策方法。

3 基于SALP 的决策方法

SALP 方法的基本思路是在给定运行点将非线性不确定系统CCP 问题近似转化为线性规划问题,并求取该点最优修正量,据此对控制变量进行修正、不断迭代,直至收敛。

3.1 含不确定变量非线性规划问题的近似线性化

为了验证Sline近似线性化模型的精度,对本文算例进行了3 000 个样本的蒙特卡洛抽样计算,以线路4-14 传输容量为例,统计其概率分布曲线,与由式（12）所得的高斯分布曲线相对比,结果如附录A图A1 所示。由图A1 可见,近似线性化模型较为精确地描述了系统状态变量的概率分布特性。

式中:Φ-1(·)为标准正态分布的累积分布函数的反函数。

类似地,可以求出fd、V、Vse、Vsh、Sse及Ssh等状态量的标准差,并将含不确定变量ΔPW和ΔPL的约束不等式近似转换为对应的线性不等式。

3.2 SALP 方法及其误差分析

经过上述变换,可将式（10）所描述的非线性不确定系统的CCP 问题近似转化为线性规划问题,即

需要说明的是,尽管近似线性化模型不可避免地存在一定误差,但由于每次迭代都重新计算当前点的灵敏度,并更新线性化模型,因此,第k次迭代的模型误差并不会影响第k+1 次迭代的模型精度,而只是改变了第k+1 次搜索的初始点,即改变了搜索的路径,最终解的精度仍然取决于收敛判据。SALP 方法的主要误差在于近似线性化模型描述系统变量概率分布特性所导致的误差,而3.1 节已证明对于超短期预测而言,近似线性化模型能较为精确地描述其概率分布特性。

由于线性化方法的局限性,SALP 方法搜索到的有可能是局部最优解,而非全局最优解。实践中可以从不同初始点出发,比较所求得的解,取其中经济代价最小的方案作为最优解,从而在一定程度上克服这一局限。

3.3 不确定变量相关性的处理

假设PW和PL服从高斯分布,且其相关系数矩阵为M,若系统的风电场数量为nW,负荷数量为nL,则M为(nW+nL)×(nW+nL)矩阵。

式中:E=diag(σW,σL),为对角阵。

进一步可推得:

将式（21）代入式（11）,由此,优化问题中只包含独立随机变量,可按照3.1 节所述方法求解。

4 算例分析

为了验证基于SALP 的校正控制决策方法的有效性,将其应用于修改后的IEEE 10 机39 节点系统,对故障后系统的校正控制策略进行了计算,有关SALP 方法的仿真使用2.3 GHz Inter i5 CPU 的电脑,应用MATLAB2014 编程实现,其中线性规划调用linprog 函数。

4.1 算例系统

IEEE 10 机39 节点系统如图3 所示,其数据详见文献［22］,系统基准容量为100 MV·A。同步发电机功率上、下限及功率调整代价因子如附录A 表A1 所示,各负荷节点的可控比例及代价因子如表A2 所示,表A3 给出了各线路的传输极限。为了研究风电不确定性对校正控制决策的影响,将位于节点32、33、35 及37 的同步发电机替换为4 个风电场（WT1 至WT4）,且风电场有功功率预测值与同步发电机发电功率相等,分别为6.5、6.32、6.5、5.4 p.u.,风力发电量约占系统总发电量的40%。设风电及负荷预测误差服从高斯分布,取σW,i=0.05,σL,j=0.03。

图3 含风力发电的IEEE 10 机39 节点算例系统Fig.3 IEEE 10-generator 39-bus test system with wind generation

假设线路4-5 发生断线故障,应用拉丁超立方抽样方法［16］生成3 000 个风电及负荷样本,计算表明,故障后线路10-13、13-14、4-14 将以较大概率出现过载现象。附录A 图A2 给出了故障前后线路13-14 传输容量的概率密度曲线,由图A2 可见,故障前线路13-14 输送功率的期望为3.3 p.u.,线路过载的概率约为7%（图A2 中阴影部分）。断线后,该线路严重过载,其过载概率接近100%。此时,若不及时采取校正控制措施,线路13-14 将会由于温升过高而被切除,并有可能引发连锁故障。

由此可见,在考虑风电不确定性的条件下,如果要求系统不依靠校正控制即满足N-1 法则,则需要将线路13-14 的传输极限提高至6.0 p.u.以上,远大于正常情况下的输送功率,这必然会造成大量的投资浪费。UPFC 可以有效地控制线路潮流,并调节节点电压,因此考虑在线路13-14 加装UPFC。

4.2 含UPFC 系统的校正控制策略分析

UPFC 参数取值如附录A 表A4 所示,以节点14 为UPFC 并联节点,故障前系统潮流与IEEE 39节点系统大致相同。暂不考虑随机变量的相关性,并取式（10）中αf、αv、αu和αline为2%,取ε=0.003,应用SALP 方法求解断线后校正控制策略,迭代20 次后解收敛,计算用时约1.0 h。计算结果表明,在UPFC 和切负荷控制的共同作用下,故障后不需要改变发电机出力即可满足静态安全要求。故障前后UPFC 控制变量设定值如表1 所示。此时,节点4、12、15 处分别切除100、5.18、15.52 MW,总切负荷量为120.7 MW,控制代价为775.4 美元。

表1 故障前后UPFC 控制变量设定值Table 1 Setting values of UPFC control variables before and after failure

需要说明的是,SALP 方法的计算量主要在于求取灵敏度矩阵,由于每次迭代都需要更新灵敏度矩阵,当不确定变量及控制变量数量较大时,灵敏度矩阵所含元素较多,其计算量较大。如果逐个计算,则耗时较多。例如本算例中含有4 个风电场、21 个负荷及6 台发电机,每次迭代需要计算32 次潮流。在实际工程中,灵敏度计算可以采用并行处理技术,这样本算例的决策速度可提高约30 倍,用时达到2～3 min。

为了验证校正控制方案的有效性,基于3 000 个样本场景,对校正控制后系统的静态安全性进行了分析。图4 给出了校正控制前后部分线路负载率的概率密度曲线对比。由图4 可见,线路4-14 故障后若不采取控制措施,其过载概率约为50%,而校正后其负载率小于0.9 的概率约为100%。类似地,控制后线路10-13 的负载率以很小的方差分布在0.71左右,这是由于该线路功率主要通过线路13-14 向外输送,而故障后线路13-14 的传输功率被UPFC控制在（3.448 7-j0.497 9）p.u.,不随场景的变化而改变,故线路10-13 功率波动也较小。

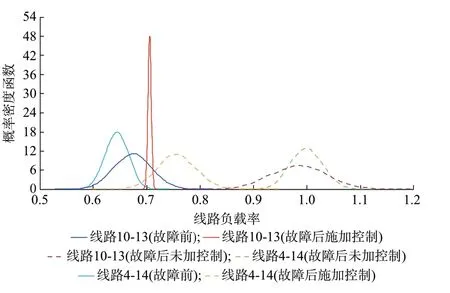
图4 校正控制前后部分线路负载率概率密度函数对比Fig.4 Comparison of probability density function of partial line load rate before and after correction control

校正控制前后系统频率偏差fd的概率密度函数对比见附录A 图A3。计算表明,故障前fd的期望为-0.001 4 p.u.,其低于fd下界（-0.004 p.u.）的概率约为0.5%。控制后由于切除了部分负荷,频率期望值增加到0.000 8 p.u.,其大于fd上界（0.004 p.u.）的概率为0.067%,因此校正控制前后系统频率均满足给定的置信区间要求。

4.3 UPFC 对校正控制策略的影响

为了进一步分析UPFC 对校正控制策略的影响,对不含UPFC 条件下的校正控制优化方案进行计算,结果如表2 所示。此时,共需减少发电机出力241.6 MW,并削减负荷276.76 MW,总经济代价为5 470.1 美元,与含UPFC 系统（见表1）相比,其控制代价大为增加。由此可见,使用UPFC 可以有效地减少负荷损失,降低控制成本。

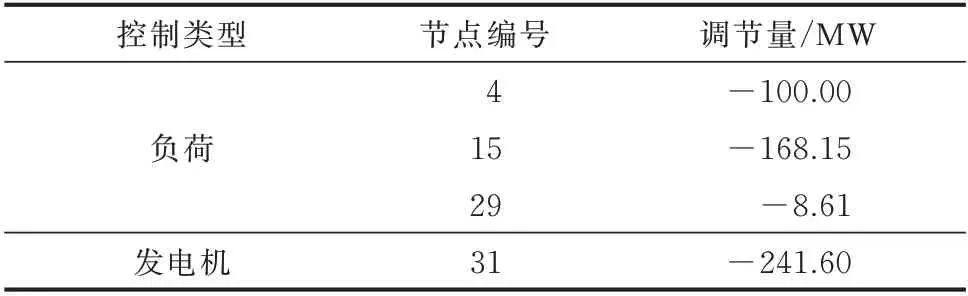
表2 不含UPFC 系统的校正控制方案Table 2 Correction control scheme without UPFC system

4.4 SALP 方法与场景法的比较

进一步,将基于SALP 的决策方法与场景法进行了对比。由于原系统含有25 个随机变量（4 个风电场出力和21 个负荷）,可能出现的场景数量庞大,难以直接分析。为了简化问题,假设系统中所有负荷具有相同的预测误差,所有风电的预测误差也相同,选择附录A 表A5 所示的9 个典型场景进行分析。

考虑到负荷及UPFC 具有更快的响应速度,本文采用了两阶段决策方法［13］,即不同场景下第1 阶段控制（发电机调节量）相同,而第2 阶段控制（切负荷量及UPFC 控制参数）则依赖于实际场景。场景法包含的变量及约束方程数量众多,是一个大规模的非线性优化问题。 为求解该问题,应用GAMS24.7 软件进行编程,使用IPOPT 求解器求解,求解器迭代1 908 次后收敛,用时386.43 s,所得控制方案如附录A 表A6 所示,控制方案平均代价为1 312.1 美元。为了验证校正控制方案的安全性,应用拉丁超立方抽样方法生成900 个场景,对控制方案进行了验算,结果表明,在给定的控制策略下系统静态安全的概率约为92%。

基于SALP 的决策方法与场景法的对比见附录A 表A7。由表A7 可知,在采用并行处理技术的条件下,基于SALP 的决策方法具有更快的决策速度,且所得策略具有更好的经济性和安全性。需要说明的是,场景法的计算用时及控制代价与场景数量密切相关,因此,场景数量对比较结果会有一定影响。

4.5 风电相关性对校正控制策略的影响

以上分析均假设随机变量相互独立,但实际系统中随机变量之间常存在一定的相关性。为简单起见,选取其中2 个风电场,对其相关性对校正控制的影响进行了分析。

由于算例系统主要面临线路过载问题,故针对PW对线路13-14 传输容量的灵敏度进行了分析。计算表明,风电场WT1 有功功率PWT1的变化对线路13-14 传输容量的影响与风电场WT2 至WT4 有功功率PWT2、PWT3及PWT4相反,即其灵敏度符号相反。故分别选取WT1、WT2 以及WT2、WT3,对不同相关性所对应的控制策略进行了计算,结果如附录A表A8 所示。由表A8 可以发现,当PWT1、PWT2由正相关逐步转变为负相关时,其控制代价逐渐加大,这是由于PWT1、PWT2对线路13-14 传输容量的影响相反,因此它们之间的正相关性有助于缓解线路过载,减小控制代价,而负相关则会加剧线路过载,加大控制代价。反之,由于PWT2和PWT3对线路13-14 传输容量的影响相同,故其相关性变化时,其控制代价呈现出与WT1 和WT2 相反的特点。

由此可见,不确定性变量之间相关性的变化对静态安全性的影响与灵敏度的性质密切相关,多个随机变量之间相关性同时变化对校正控制策略的影响较为复杂,难以一概而论。

5 结语

本文提出了一种基于SALP 的含UPFC 风电系统静态安全校正控制决策方法,提出:1）将潮流计算与UPFC 解耦,采用计及频率变化的增广潮流,全面分析静态频率、电压安全性及线路过载问题；2）基于SALP 方法将非线性不确定系统CCP 问题近似转化为线性规划问题,快速求解校正控制优化策略；3）应用Cholesky 分解法将相关随机变量转换为独立变量,分析了变量相关性对校正控制策略的影响。基于修改后IEEE 10 机39 节点系统的仿真结果表明,SALP 方法可快速高效地求解含不确定变量的非线性优化问题。同时,利用UPFC 可有效减少发电机调节量及切负荷量,显著降低校正控制成本。

本文的研究还存在一些局限,例如:1）基于SALP 的校正控制决策方法还有待大规模系统的考核,特别是采用并行处理技术后算法的计算效率和速度需要进一步验证；2）针对非高斯分布不确定系统的SALP 方法有待研究。研究表明,风电、负荷预测误差并不严格服从高斯分布,如何处理该问题尚有待研究,这也将是下一步工作的重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。