考虑运行可靠性的电力系统辅助调频控制

齐 亮，王 越

（中国农业大学信息与电气工程学院,北京市 100083）

0 引言

近年来,随着煤炭、石油等化石能源的日趋枯竭,以风能和太阳能为代表的可再生能源发电越来越受到重视。截至2020 年底,中国的风电和光伏发电并网容量分别为280 GW 和250 GW,可再生能源并网容量位居世界第一。预计到2025 年,中国的可再生能源发电量占全社会用电量的比重将达32%。由于可再生能源机组出力的随机性,大量接入或会破坏电力系统惯性,故对电力系统的频率控制提出了更高层次的要求［1］。

传统频率控制环节主要包括一次调频、二次调频、三次调频［2］。一次调频在系统出现功率扰动后即开始动作,以频率偏移为代价换取系统的实时功率平衡；二次调频通过自动发电控制（automatic generation control,AGC）重新分配调度计划内的机组出力,以消除一次调频的频率偏移；三次调频则是通过重新配置整个系统的运行备用容量和爬坡能力,恢复系统的二次调频能力。笼统而言,二次调频和三次调频都可视为辅助调频,在维持一次调频能力的同时,前者侧重经济性、后者侧重可靠性。可再生能源渗透比例的逐年递增不断地挑战上述传统调频机制［3］,给传统电力系统的安全稳定运行带来了严峻的挑战,改善高渗透率可再生能源并网的频率调节特性是目前各国电力系统亟待解决的焦点问题。

对于可再生能源系统的调频控制研究主要可以分为频率响应机理研究和控制策略研究。频率响应机理研究主要是通过分析高比例可再生能源并网后的电力系统频率响应特性,进而提出兼顾精度和速度的系统频率响应模型［4-5］。随着风电并网容量的不断攀升,针对风电系统的频率控制策略成为关注的焦点,如频率响应区间划分的机组惯量模糊自适应控制方法［6］,基于自适应动态模型的在线强化学习方法［7］,基于虚拟惯量的改进频率控制策略［8］等。而对于控制策略的研究,主要是考虑对AGC 进行优化控制,以提高调频效果［9-10］。文献［11］依靠提前预测的功率扰动以及储能等动态数据,结合动态仿真和多目标网格自适应搜索算法,提出一种储能系统辅助传统机组协调参与AGC 的优化控制策略,经仿真对比验证了该方法能够对系统调频能力实现持续优化。文献［12］提出了分层递归人工神经网络的AGC 优化策略,能够平稳地解决AGC 响应问题,并与基于粒子群算法的比例-积分-微分（PID）控制方法进行了对比,显示了其在调频性能上的优越性。文献［13］设计了一种时变预测优化PID 控制策略,以时变预测优化模型表征风速变化对AGC 的影响,以PID 控制器对前级预测优化控制变量的输出结果进行调整,验证了当风电参与频率控制时,所提方法具有更好的调频效果。然而,现有的AGC 策略研究对可再生能源的随机性考虑不足,也缺少对于系统运行可靠性的考量。

随着电力系统运行数据的不断积累,运用运行可靠性理论研究不确定因素下的系统运行管理问题已持续开展多年［14-17］,逐渐发展出一些运行备用不足风险的评估方法。例如,文献［18-19］提出了系统旋转备用风险的概念,并基于交叉熵理论提出了评估旋转备用风险指标的高效计算方法。目前,对于如何运用这些运行风险指标指导系统调频控制的研究并不多见。

本文提出一种考虑运行可靠性的辅助调频控制方法。该方法将系统运行可靠性指标——期望缺供电量（expected energy not supplied,EENS）［20］作为参考控制量,设计了比例-积分（PI）负反馈控制回路实现可调度机组出力的预防性调节,通过系统辨识技术并结合Jury 稳定性判据,建立了PI 控制参数的跟踪调节方法,有效改善了系统频率响应。

1 考虑运行可靠性的调频模型框架

1.1 运行可靠性指标

电力系统运行可靠性是指计及设备健康状况、外部环境条件、系统运行条件和运行规则等,电力系统在规定时间内持续向用户输送电力的能力量度［21］。常见的用于衡量系统运行可靠性的指标包括EENS、失负荷概率、供电可用率等。本文借助EENS 阐述运行可靠性辅助调频的基本思想。按照IEEE 标准,EENS 是指系统在给定时间内因发电容量短缺或网络安全约束造成负荷电量削减的期望数［22］。EENS 被广泛应用于变电站、发输配系统的可靠性评估问题,也可用于系统薄弱环节识别以及考虑可靠性的设备检修方案优化。EENS 指标REENS的一般化表达式为:

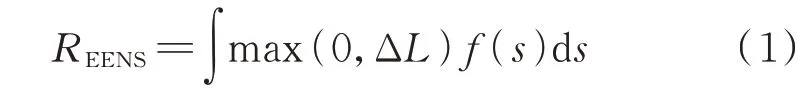
式中:ΔL为负荷总功率需求与可用发电容量之差；f(s)为运行场景s的联合概率密度。当忽略网络约束时,运行场景由机组运行状态、可再生能源和负荷预测三者组合决定。

对于单台发电机组,因故障后在所考虑的运行时间尺度（如Δt=15 min）内无法完成修复,在运行可靠性的研究中,一般可将Δt内发生故障的概率p和故障率θ之间的关系近似表达为p=1-e-θΔt,Δt定义为前置时间［23］,是指从当前时刻开始直到新增的备用容量准备完毕,可以并网发电所需要的延迟时间。若需考虑运行环境和荷载条件的影响,也可以建立与外部因素的关联概率模型［24］。值得注意的是,受实际数据获取条件的限制,机组实时故障率或无法精确统计,在实际应用中多以年平均故障率来代替,此时EENS 可主要反映系统运行可靠性随可再生能源和负荷水平的变化。对于风电、光伏以及负荷等随机性较强的功率预测,也可以选择Copula 模型表达联合出力的随机性［25］。

由式（1）可知,REENS取决于可再生能源和负荷的误差分布以及机组可靠性,其数值越大系统可靠性越低,可通过调整机组出力,对REENS加以抑制。例如,当某一机组c故障时,其他所有参与调频机组的总可用出力增量为:

在短期运行时间尺度Δt内,若忽略负荷和风机出力的预测误差以及2 台及以上机组同时故障的小概率事件,将式（3）代入式（1）可以得到REENS的近似表达式:

式中:Pmin、Pmax分别为调频机组i允许的有功出力最小值和最大值。

综上,通过调整调频机组出力可以优化REENS,表达式如下:

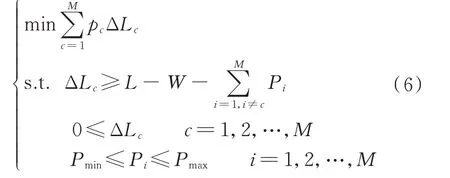
Pi为待优化的决策变量,其他均为给定常数,作为线性规划问题,可以采用单纯形法快速求解。

1.2 EENS 辅助调频原理

通过求解式（6）的线性规划问题,可以方便得到REENS最小时各个机组的相应出力,作为机组出力参考值进行出力再分配。考虑到实际系统受到网络约束以及多种随机因素的影响,机组出力与REENS之间往往表现出复杂的非线性关系,式（6）的约束条件仅为约束条件的子集,故所求解的REENS最小值必然小于REENS的实际最小值,实质为松弛解,而实时的REENS可借助运行可靠性评估方法进行估计［14-17］。采用式（6）近似求解REENS最优值的优势在于,可以保证实时评估的计算效率,与REENS实时评估结果之差作为PID 输入,对机组出力进行再分配,实现对系统运行可靠性的渐进跟踪调节。本节阐述基于PID的EENS 控制环节,以实现考虑运行可靠性的辅助调频。

首先,将式（6）计算得到的系统REENS最小值设定为参考值,记为Rref,用于反映当前负荷状态下,系统运行可靠性最高所对应的各机组出力分配情况。值得注意的是,因系统的运行方式会发生调整以及存在负荷波动,Rref需要根据式（6）滚动计算。再根据实时网络状态、故障率、负荷及可再生能源等系统信息,借助运行可靠性评估方法实时评估计算REENS［18］。将以上2 个量的差值记为ΔREENS,即

式中:Popt,i为通过式（6）计算的机组i的出力；PAVG为所有调频机组当前的平均出力。

综上,本文在传统一、二次调频的基础上增设了EENS 辅助调频环节,通过监测系统运行可靠性水平补充系统的一、二次调频能力,以提前应对潜在的大功率扰动风险,本质上是一种考虑了功率随机特征的预防性调频控制。后文算例分析也证实,通过EENS 辅助调频环节对机组出力的再分配,可有效改善功率扰动下的系统频率响应特性。

上述EENS 辅助调频环节的简化框图如图1所示。

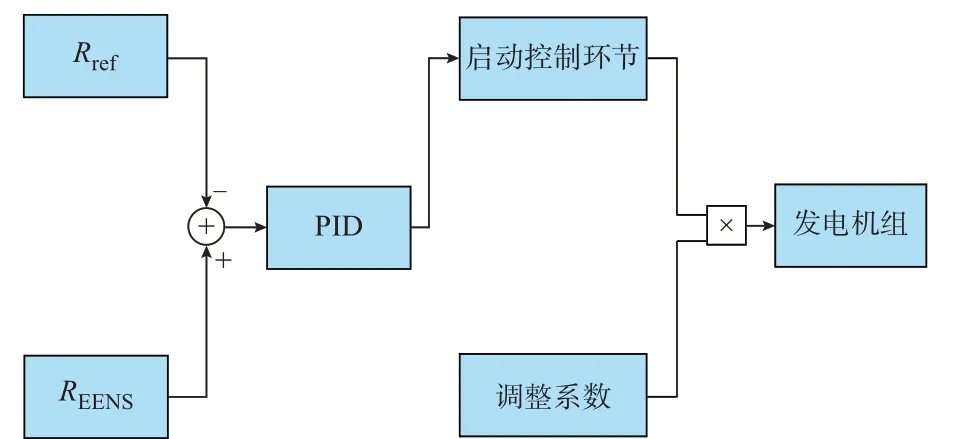
图1 EENS 辅助调频环节的简化框图Fig.1 Simplified block diagram of EENS auxiliary frequency regulation link

2 基于Jury 判据的参数整定

EENS 辅助调频环节的PID 参数整定依赖于受控系统的调频特性。鉴于系统运行工况随运行方式调整动态变化,系统传递函数并非恒定,有必要对PID 参数进行自适应调整。本文提出应用系统辨识技术对原始高阶多机系统模型进行降阶辨识,并基于降阶辨识模型,应用Jury 判据,对EENS 辅助调频环节的PID 参数进行自适应整定。

2.1 模型的系统辨识

考虑运行可靠性的电力系统辅助调频系统降阶辨识的基本原理［26］如图2 所示。图中:fi、fo分别为辨识过程的输入和输出信号；H为系统惯性时间常数；D为阻尼系数；G(z)为受控系统的高阶传递函数；C(z)为PI 控制器的传递函数,表达式见式（9）。

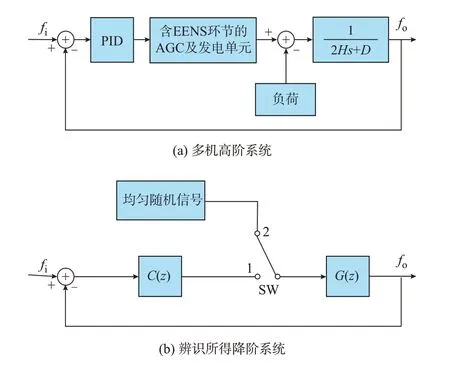
图2 考虑运行可靠性的辅助调频系统降阶辨识图解原理Fig.2 Principle illustration of order-reduction identification for auxiliary frequency regulation system considering operational reliability

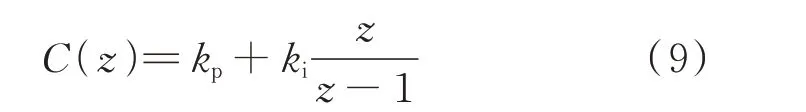
式中:kp和ki为待求参数。

在进行系统辨识时,首先,将开关SW 拨至2,再使用外部均匀随机信号作为激励,在给定的采样时间下,对输入数据和输出数据进行采样。上述过程可借助成熟的系统传递函数辨识方法完成［27］,从而得到开环低阶离散传递函数G′(z)。

对于图2 所示的频率响应系统,其闭环传递函数Φ(z)与G′(z)和C(z)的关系为:

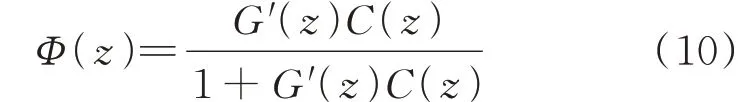
2.2 PI 控制器参数估计

由式（10）可得降阶离散系统的闭环特征方程为:

式中:a0,a1,…,an为特征方程的各阶系数。

对式（12）应用Jury 判据,可以求取kp和ki的稳定范围。Jury 判据是在z域内应用的稳定判据,它类似劳斯判据,能根据一个离散系统的闭环特征方程的系数,判断其根是否位于z平面的单位圆内,从而得出系统稳定与否的结论［28］。首先,需要按照一定规则构造Jury 阵列,其形式如表1 所示。

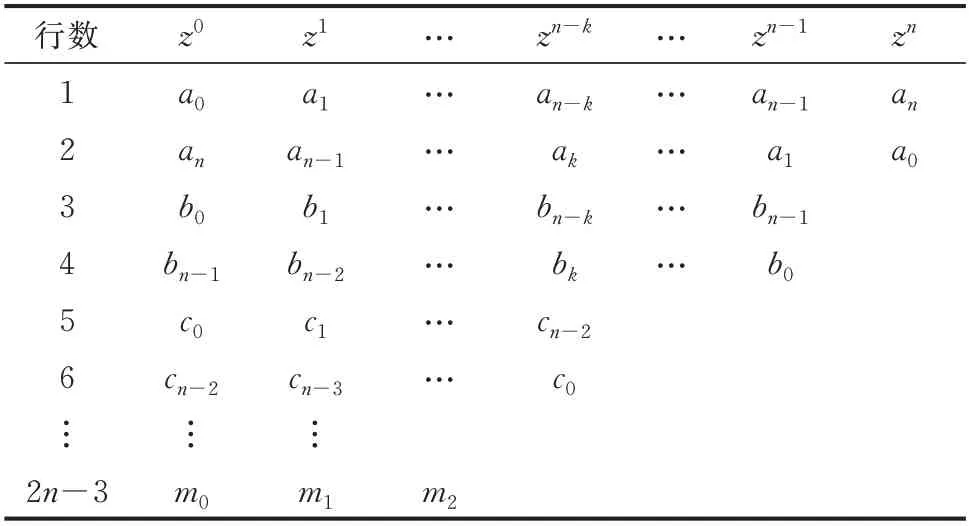
表1 Jury 阵列Table 1 Jury array

构造方法如下:

1）特征方程式（12）的系数按从低到高次幂排列为第1 行；

2）偶数行由上一紧邻奇数行倒序排列而成；

3）从第3 行起的各奇数行,每个元素采用下式计算:

第3 行:

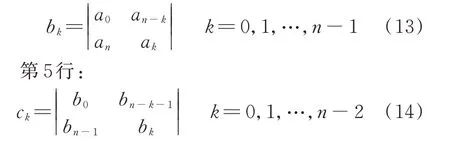
以此类推,直到最末行仅能计算出3 个元素为止。

根据上述Jury 阵列判断特征方程D(z)=0 的根全部位于z平面上单位圆内的充分必要条件是:D(1)＞0,(-1)n D(-1)＞0,|a0|＞an,以及|b0|＞|bn-1|,|c0|＞|cn-2|,…,|m0|＞|m2|。应用该充要条件即可求出PI 控制器kp和ki的参数范围。

综上,对EENS 辅助调频环节的PI 控制参数估计的主要步骤为:

步骤1:根据系统的发电机组相关信息,由式（6）计算出REENS最小值,作为EENS 辅助调频环节的参考值Rref。

步骤2:按图2 对模型加入外部信号并记录输入输出数据,对系统进行辨识得到降阶传递函数G′(z)。

步骤3:根据G′(z)和PI 控制器传递函数C(z),以kp、ki作为待求变量,由式（12）列写闭环特征方程D(z)的各阶系数。

步骤4:按Jury 阵列的构造规则,列写出Jury阵列。

步骤5:根据Jury 稳定判据,列出含kp、ki的不等式组并求解其范围。

利用运动与远程通信系统,针对监测到的系统运行工况变化,如负荷突增或发电机故障造成的功率干扰,仅需在仿真系统中调整相应部分的模型,再由计算机系统重复降阶辨识过程并应用Jury 判据,即可实现PI 控制器参数的自适应整定。

3 算例分析和仿真结果

3.1 PI 参数可行范围

为验证所提的EENS 辅助调频环节的有效性,本文以含10 台发电机的微电网调频控制系统为例进行仿真验证。10 台发电机组的基本信息如表2 所示,机组详细传递函数参见文献［29］。另外,系统原始负荷为500 MW,设置负荷干扰为50 MW,前置时间为1.5 min,所有机组爬坡率均为2.7 MW/min。以下算例中,根据式（6）所得的Rref耗时仅9.95 ms,对控制环节的响应速度影响可忽略不计。

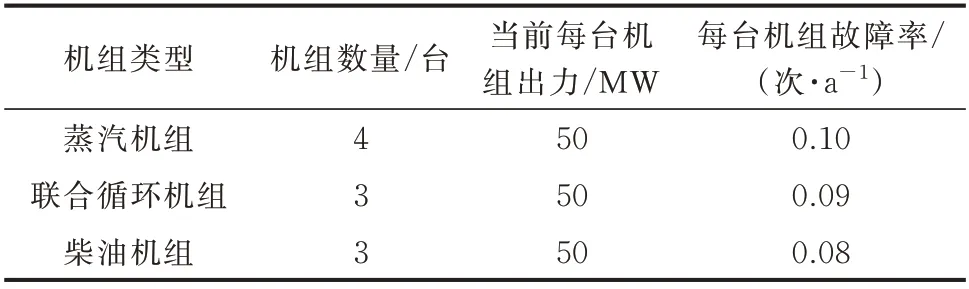
表2 发电机组仿真参数Table 2 Simulation parameters of power generators

应用2.1 节提出的系统辨识方法,输入一个均匀分布的随机信号,其最大、最小值分别取0.1 和-0.1。采用MATLAB 系统辨识工具得到当前运行状态下的系统降阶传递函数G′(z)为:

对上述参数范围的有效性进行验证。分别设定ki等于1/2、1/4、1/8、1/16、1/32、1/64、1/128 的边界值（31.047）进行考察,仿真结果汇总于表3。

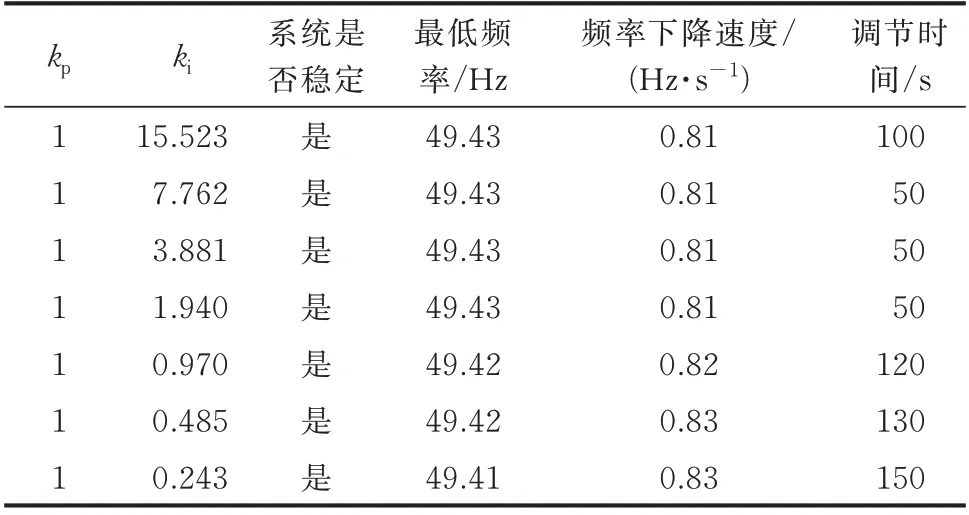
表3 kp固定、ki变化时的频率响应Table 3 Frequency response when kp is fixed and ki varies

实验表明,在ki的稳定取值范围内,系统的频率输出均表现稳定。综合考虑最低频率、频率下降速度以及调节时间3 项指标时,1.940≤ki≤7.762 可获得更好的调频效果。

给定ki的范围,对参数kp的范围进行考察。首先选定ki=7.762,再确定kp辨识值上限为11.642,将其作为仿真实验基准值,分别取11.642 的1 倍、1/2、1/4、1/8 和0 进行实验,系统均保持稳定,且最低频率为49.43 Hz,调节时间为50 s,频率变化率为0.81 Hz/s,所以0＜kp＜11.642 是符合要求的。

在上述过程中,降阶传递函数是基于给定采样时间内的输入、输出数据,经过成熟的辨识技术拟合得到,然后经多次试验,其拟合率基本可维持在90%以上,即简化降阶模型可以准确地模拟仿真系统,加之后续利用Jury 稳定性判据求取PI 控制参数的范围并进行有效性验证,可以进一步提高此方法的准确性。

为了阐明PI 控制参数改变对调频机组出力调整量,进而对频率响应效果的影响,本文选取几组不同的PI 参数,得到某一调频机组出力调整量的变化情况如图3 所示。

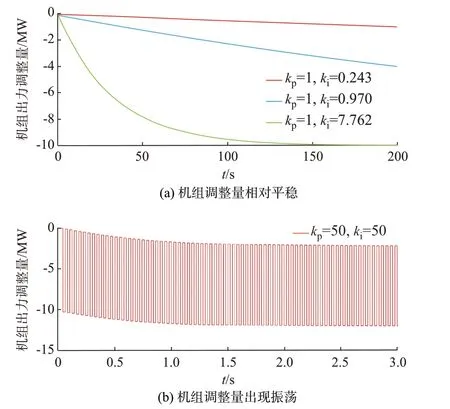
图3 不同PI 参数下调频机组出力调整量的变化Fig.3 Changes in power output adjustment of a frequency regulation unit with different PI parameters

结合表3,从图3（a）可以观察到,优选的参数组合（kp=1,ki=7.762）可以确保在出现大扰动前将机组出力调至最佳水平,从而最有效地发挥其调频能力。而较小的参数组合（kp=1,ki=0.970 或kp=1,ki=0.243）下调整机组出力的速度较慢,在大扰动前未能将机组出力调至最佳,导致频率响应效果逊于优选参数,但经仿真验证,其频率响应仍优于未加入EENS 辅助调频环节的情形。因此,频率响应的改善主要归功于EENS 辅助调频环节的加入,PI 参数的自适应整定可进一步优化频率响应特性。

而某些超出Jury 判据整定范围的参数组合（如kp=50,ki=50）可能使机组出力调整量出现振荡,从而导致系统不稳定,如图3（b）所示。

3.2 仿真对比结果

利用MATLAB/Simulink 搭建传统的频率响应模型和本文设计的含EENS 辅助调频环节的频率响应模型,并选取kp和ki范围中的一组参数（kp=1,ki=7）。传统模型即传统的一、二次调频系统,其出力分配服从一、二次调频的一般规律,且部分机组濒临最大出力上限,与本文所提模型的唯一区别是不含EENS 辅助调频环节,无法进行预防性调节和释放调频能力。对2 个模型的频率响应效果分别进行仿真,对比结果如图4 所示。可以观察到,未加入EENS 辅助调频环节时,系统最低频率为49.35 Hz,调节时间约为150 s；而加入了EENS 辅助调频环节后,最低频率升至49.43 Hz,提升幅度0.16%,调节时间缩短至50 s。

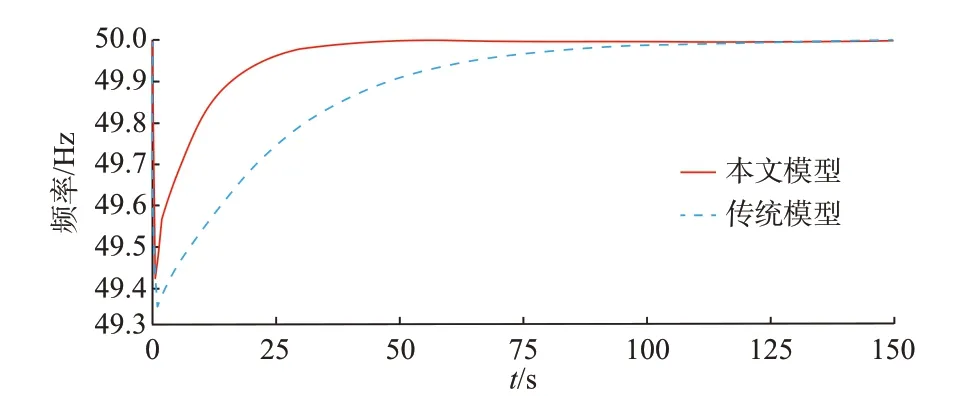
图4 加入EENS 辅助调频前后的频率响应对比Fig.4 Comparison of frequency responses with and without EENS auxiliary frequency regulation

含EENS 辅助调频环节的模型和传统模型的某2 台机组出力曲线对比如图5 所示。可以看出,传统模式下,由于1 号联合循环机组濒临最大出力上限,在调频过程中,其出力达到了自身的出力上限（55 MW）而无法继续参与调频,其他未达到出力上限的机组正常参与调频。而含EENS 辅助调频环节的模型,可以提前将包含1 号联合循环机组在内的濒临出力上限机组的出力分配到1 号柴油机组及其他机组,这样就可以在出现大功率扰动前,释放一、二次调频能力。随着一、二次调频作用使得频率恢复正常,当满足EENS 辅助调频环节启动条件后,再将机组出力进行新一轮分配。

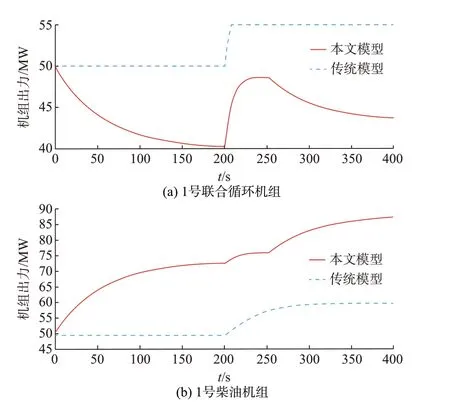
图5 加入EENS 辅助调频前后的机组出力变化Fig.5 Variation of unit power output with and without EENS auxiliary frequency regulation

ΔREENS趋近于0 的耗时可用于反映EENS 辅助调频环节的调节性能,历时越短则调节速度越快。上述仿真过程中,ΔREENS的表现如图6 所示。可以看出,ΔREENS在仿真启动时的初始值大于0,随着EENS 辅助调频环节对发电机组出力不断调整,ΔREENS逐渐趋近于0,系统可靠性逐渐提高。200 s时设定出现负荷突增,致使ΔREENS＜0。随着一、二次调频发挥作用不断增加机组出力,ΔREENS增大至正数,频率也逐渐恢复正常,当满足EENS 辅助调频环节启动条件后,ΔREENS再次趋向于0,使得系统运行可靠性在新负荷水平下调节至最高。

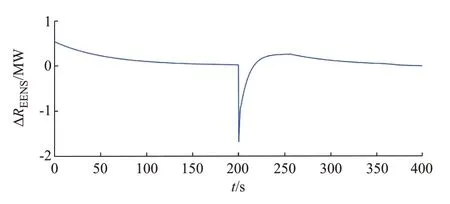
图6 ΔREENS 曲线Fig.6 Curve of ΔREENS

以上仿真结果表明,EENS 辅助调频环节在出现功率扰动前能够有效发挥辅助调频作用,使得系统中各机组出力可以渐进达到当前负荷下运行可靠性最高的情形。对于大负荷干扰,这种预防性调节可以有效改善系统频率响应特性。

为观察前置时间Δt对于EENS 辅助调频性能的影响,分别取Δt为0.5、1.0、1.5 min,观察系统频率响应性能以及ΔREENS归零时间,结果汇总于表4。

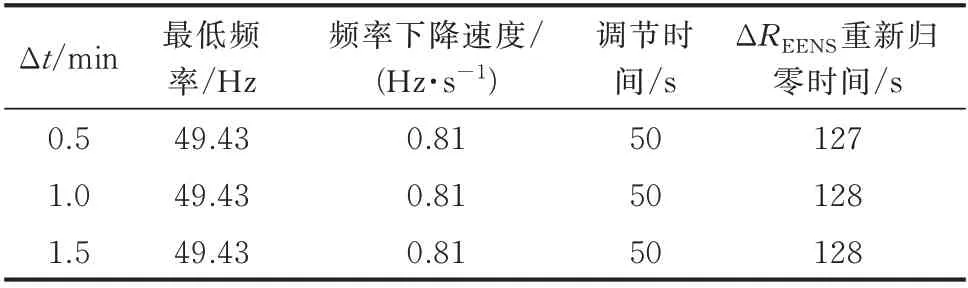
表4 不同Δt 取值下的系统频率响应和ΔREENS 归零时间Table 4 System frequency response and ΔREENS reset time with different values of Δt

可见,系统最低频率、频率下降速度、调节时间以及ΔREENS的归零时间都与Δt的关系不大,这说明EENS 辅助调频环节对前置时间Δt的设定不敏感,实际应用时,对Δt参数整定要求不高。

为验证加入风电机组后的频率调节特性,本文采用文献［30］的风速模型。它由阵风、渐变风、随机风等模型组成,能较好地描述风速随机性、渐变性。将上述风速模型加入变速风力发电机模型［31］,风电机组的额定功率为18 MW。

风电机组不参与调频,主要是为了验证在出力随机性较强的情况下,EENS 辅助调频环节的作用。加入该风电机组的情况下,加入EENS 辅助调频环节前后的系统频率响应特性如图7 所示。由图可见,在接入风电机组的情况下,系统的最低频率表现和频率恢复时间都有明显改善。同时,最低频率提升了0.18%,超过未加入风电机组情况下的最低频率提升百分比（0.16%）,说明风电机组加入后,EENS 辅助调频环节的作用更加显著。

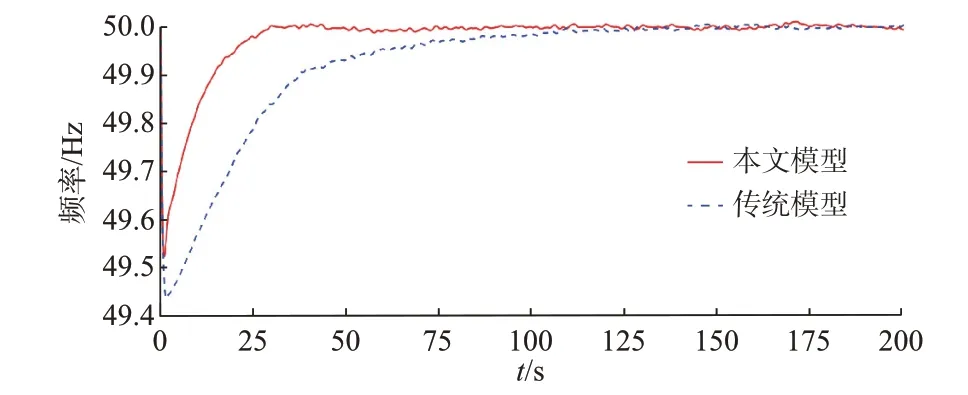
图7 加入EENS 辅助调频前后含风电机组的频率响应Fig.7 Frequency responses with wind power turbines before and after EENS auxiliary frequency regulation is adopted

通过上述仿真可知,若传统的一、二次频率响应令部分机组出力接近甚至达到额定容量时,一旦出现负荷干扰,系统的最低频率会更低,调频时间也会增加,而加入EENS 辅助调频环节之后,能够在出现大的功率扰动前,以运行可靠性最优为目标,将出力接近甚至达到额定容量机组的有功功率,部分转移给其他机组,令整个系统在当前负荷下的可靠性达到最高,一旦出现负荷干扰,相比于传统的频率响应模型,最低频率和调频时间都会得到明显改善。

4 结语

本文提出一种考虑运行可靠性的电力系统辅助调频控制方法。该方法设计了EENS 的PI 控制环节,作为传统一、二次调频模型应对功率随机波动的调频手段补充。提出利用系统辨识和Jury 判据的方法确定PI 控制器参数取值范围,通过仿真表明,将可靠性指标EENS 引入电力系统调频系统之中,可提高调频效果,调频时间、最低频率及频率下降速度都获得了不同程度的改善,同时,加入风电机组后,EENS 控制环节的辅助调频作用愈发明显。

目前的研究尚未考虑风电机组参与调频的情况,如何将EENS 控制环节引入风电机组参与调频的系统,配合更加快速、准确的参数调节方法,改善大功率扰动下的频率响应将是下一步工作的研究重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。