互联网金融风险测度与数值分析
——基于g-VaR模型
2022-04-18马慧子刘翠翠王向荣
马慧子,刘翠翠,2,林 琳,王向荣
(1.山东科技大学 数学与系统科学学院,山东 青岛 266590; 2.山东女子学院,山东 济南 250300)
互联网金融是资金供需双方通过信息中介平台直接进行交易,在金融中介参与度大幅降低的情况下实现投资人财产增益的理财管理通道,是支付、投资和信息中介服务的新型金融业务模式[1-2]。作为互联网金融的重要组成部分,互联网理财产品主要包括互联网货币基金、股权众筹、P2P网络借贷、比特币等投资理财产品。与传统银行存款理财相比,互联网理财产品具有相对收益率高、去中心化程度高等特点。互联网理财产品在快速发展的同时,进一步提升了我国普惠金融服务效率,完善了我国金融体系结构,在推动我国国内大循环、国际国内双循环发展过程中发挥了积极作用。
以“余额宝”为代表的互联网理财产品充分发挥资源和技术优势带动了民生金融的发展,同时也使市场风险波动性更加复杂。Bengtsson[3]和张瑾等[4]的研究均表明,货币基金的流动性错配会加剧流动性问题,进而增加市场系统性风险。陈荣达等[5]指出,互联网金融发展指数、利率期限结构调整的债券市场收益率等也对互联网金融理财产品信用价差存在显著影响。董小君等[6]利用PVAR模型研究了互联网金融市场中的各类风险,发现信用风险对金融深化程度低的地区影响较大,而流动性风险对金融深化程度高的地区影响较大。Yang等[7]在对余额宝的研究中指出,流动性风险是互联网理财产品的最大难题,金融机构现金流不足将影响声誉,但储备的现金过多又可能错失投资机会。
根据以上分析可以看出,互联网理财产品所面临的风险与传统理财产品相比更具不确定性。传统的可加概率或线性期望不能完全解释这种风险不确定问题,需要寻找更为有效的不确定风险度量方法来度量互联网理财产品市场的风险问题。非线性期望可以有效地拟合变量间的非线性关系,捕捉极端、不确定性风险。本研究从非线性期望理论出发,以互联网理财产品为例,探索互联网金融市场风险的非线性度量分析。
1997年,Pardoux等[8-9]基于倒向随机微分方程(backward stochastic differential equation,BSDE)引出了动态非线性数学期望理论g-期望概念,并证明g-期望是一种典型的非线性数学期望。此后,g-期望在金融研究中得到了进一步应用。Gianin[10]使用g-期望来度量不确定风险的问题,提出通过有条件的g-期望可获得基于g的动态风险度量。Jiang[11]探讨了g-期望的凸性、次可加性及相关风险度量。Chen等[12]在g-期望框架下讨论了静态风险测度与动态风险测度的关系。Hu等[13]在g-期望框架下研究了Fubini定理。马慧子等[14]利用正倒向随机微分方程研究了期权定价模型。纪荣林等[15-16]证明了g-期望的凸性、条件凸性,建立了倒向随机微分方程生成元与相关动态凸风险之间的对应关系。
部分学者进一步探讨了g-期望在股票、债券等金融市场风险测度中的应用。宫晓琳等[17]分析了非线性期望理论在风险测度中的实际应用及其不确定性因素,认为g-期望理论将对金融市场系统性风险研究产生深远影响。Jiang等[18]分析了g-期望下市场中无风险债券和风险股票在有限交易区间内的最优效用。杨碧璇等[19]利用g-期望描述成本函数并讨论了资产负债管理博弈问题。Chen等[20]探讨了基于风险的最优投资和比例再保险问题,假设保险公司盈余过程和金融市场风险资产过程是一般的跳跃扩散过程,并利用g-期望产生的凸风险测度描述了投资和再保险的终端财富风险,以风险最小化为目标,利用随机极大值原理对问题进行了求解。
尽管g-期望理论已经被应用于金融研究领域,但基于g-期望理论解决概率模型未知、非线性期望下的互联网理财产品风险度量问题还需要进一步探讨,互联网理财产品数据大、参数假设复杂等特征也增大了g-期望在理论研究和实践活动中的应用难度。在此背景下,本研究参照互联网理财产品数据分布特征和风险特性,结合g-期望理论和在险价值(value at risk,VaR),构造基于非线性期望理论的g-VaR风险度量模型并借助数值算法进行实验分析,以探索解决互联网理财产品风险测度的新方法和新途径。
1 倒向随机微分方程与g-期望
1.1 倒向随机微分方程
一般倒向随机微分方程的微分形式可以表示为:
(1)
积分形式为:
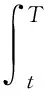
(2)


通常g满足的假设有:
A1) (Lipschitz条件)存在一个常数C≥0,使得∀t,y1,y2,z1,z2有:
|g(t,y1,z1)-g(t,y2,z2)|≤C(|y1-y2|+|z1-z2|);
A3)P-a.s.,∀(t,y),g(t,y,0)=0;
A3′)P-a.s.,∀t,g(t,0,0)=0;
A4)P-a.s.,∀(y,z),t→g(t,y,z)是连续的。
1.2 g-期望
对函数g(y,z,t):R×Rd×[0,T]→R,考虑下列假设条件:



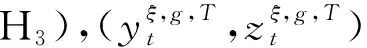
定义风险度量ρ是从L2(Ω,FT,P)到R的映射。考虑BSDE
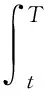
(3)
其中X∈L(Ω,FT,P),构造风险度量ρg:
L2(Ω,FT,P)→R,有ρg(y)=εg[-φ(y)],
(4)
其中φ(y)为单调递增凹函数。
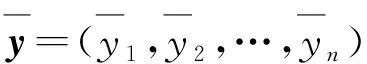
(5)
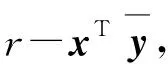
2 基于g-VaR的风险度量
在险价值(VaR)是指在一定的概率水平下,某一金融资产或证券组合在一定持有期内预期的最大可能损失值,见式(6)。
Prob(Δp≤VaR)=α,
(6)
其中,Δp为资产组合在持有期Δt内的损失,α为给定的置信水平。
考虑到VaR忽略了发生巨大损失的小概率情况,将g-期望与VaR结合,构造g-VaR风险度量模型,用于衡量互联网理财产品市场变化所带来的投资人预期收益与实际收益发生偏离的可能性。
以互联网金融中最具代表性的互联网理财产品为例,在给定的置信水平下,某一互联网理财产品组合在未来特定时期内,预期收益与实际收益可能发生的最大偏离即最大损失。定义表达式为:
g-VaR=inf{β∈R:εg[Ι(r-φ(y))+<β]≤α}。
(7)
设资产组合的初始价值为w0,w为该互联网理财产品组合的期末价值,期末的期望收益率为Y,在给定的置信水平下,期末资产组合的最小价值为w*=w(1+Y*),其中Y*为相应的最低收益率。则g-VaR可定义为相对均值的最大可能损失:
g-VaR=εg[w]-w*=εg[w0(1+Y)]-w0(1+Y*)=w0(εg[Y]-Y*)。
(8)
其中Y=r-xTy。
εg[r-xTy]可利用倒向随机微分方程求解。由于倒向随机微分方程可以看作金融市场中的一个定价机制,而起决定作用的是生成元g。因此,首先寻找特殊的生成元函数g,构造新的倒向随机微分方程。
假设互联网理财产品存在1种风险非常低的资产(无风险资产)和a种风险资产,其价格方程Pt,St分别满足:
(9)
(10)
其中,r、μ、σ都是常数。
通常余额宝被认为是互联网理财产品中的“国库券”,其“T+0”赎回制度以及巨大的资金规模保障了该理财产品收益的稳定性,因此可被视为互联网理财产品中的无风险资产。与余额宝等“宝宝类”货币基金相比,P2P理财、众筹乃至虚拟货币投资等互联网理财产品具有较高投资风险,可被视为风险资产。
考虑自融资策略,设其价值过程为yt,yt=Pt+aSt(0≤t≤T),则
dyt=dPt+adSt, 0≤t≤T。
(11)

(12)
(13)
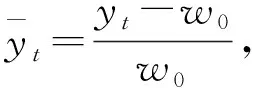
(14)
则对应的BSDE可表示为:
(15)

(16)

最终得到构造的BSDE为:
(17)
该倒向随机微分方程存在唯一解,解为:
(18)
由g-期望的定义知
(19)
代入式(18)得
(20)
则可得到g-VaR的表达式为:
(21)
3 基于g-VaR的数值分析
根据定义,g-VaR可以通过求解BSDE(式(15))来获得,但在许多实际问题中通常无法得到BSDE精确的显式表达式[16],需要借助BSDE的数值方法求解式(15)。
首先,考虑一般形式的BSDE:
(22)
其中,t∈[0,T]。然后,引入时间区间[0,T]的一个一致剖分T,
T:0=t0 这样,可将BSDE(式(22))限制在每一个小区间上进行研究,即 (23) 对式(23)中的倒向方程取条件期望Etn[·]=E[·|Ftn],可得到第一个参考方程: (24) 但观察式(24)发现,ytn,ztn都是需要求解的未知量,还需要第二个参考方程。为此,先在式(23)中倒向方程的等号两侧同时乘以布朗运动的增量ΔBtn+1=Btn+1-Btn,然后在等式两侧同时取条件期望Εtn[·],可得 (25) 以式(24)和式(25)为基础,对参考方程中的积分进行数值逼近,可得到各类求解BSDE(式(23))的数值方法。 考虑到式(24)和式(25)中出现的积分都是确定性积分,被积函数也是确定性的,故可以使用Euler方法对其进行估计: (26) 其中,Ry、Rz是截断误差,以此为基础提出下面求解BSDE的Euler格式。 给定随机变量X0、YN和ZN,通过求解以下方程组得(Yt,Zt)在tn处的数值解(Yn,Zn),其中n=N-1,…,1,0。 Yn=Etn[Yn+1]+Δtng(tn,Xn,Yn,Zn),ΔtnZn=Etn[Yn+1ΔBn+1]。 在每个小区间[tn,tn+1]上Euler格式对应数值算法1。其中,E(tn,Xn)=(Etn[Yn+1],Etn[Yn+1ΔBtn+1])。 算法1 求解BSDE的Euler格式 Input:tn,Xn,EtnYn+1 ,EtnYn+1ΔBtn+1 ,ε Output: Yn,Zn 1) function ALG. BSDE. Eu(tn,Xn,E(tn,Xn)) 2) Zn←(1/Δtn)EtnYn+1ΔBn+1 3) l←1 4) Yn,l←EtnYn+1 5) Yn,l+1←EtnYn+1 +Δtng(tn,Xn,Yn,l,Zn) 6) whileYn,l+1-Yn,l>ε do 7) l←l+1 8) Yn,l+1←EtnYn+1 +Δtng(tn,Xn,Yn,l,Zn) 9) end while 10) Yn,l←Yn,l+1 11) return (Yn,Zn) 12) end function 使用矩形公式对确定性的积分进行估计,可以得到Crank-Nicolson格式。 算法2 求解BSDE的Crank-Nicolson方法 Input: tn,Xn,EtnYn+1 ,EtnZn+1 ,Etngn+1 ,EtnYn+1ΔBtn+1 ,Etngn+1ΔBtn+1 ,ε Output: Yn,Zn 1) function ALG. BSDE. CN(tn,Xn,E(tn,Xn)) 2) Zn←(2/Δtn)EtnYn+1ΔBtn+1 +Etngn+1ΔBtn+1 -EtnZn+1 3) l←1 4) Yn,l←EtnYn+1 5) Yn,l+1←EtnYn+1 +12Δtng(tn,Xn,Yn,l,Zn)+12ΔtnEtngn+1 6) while Yn,l+1-Yn,l>ε do 7) l←l+1 8) Yn,l+1←EtnYn+1 +12Δtng(tn,Xn,Yn,l,Zn)+12ΔtnEtngn+1 9) end while 10) Yn,l←Yn,l+1 11) return (Yn,Zn) 12) end function Euler方法和Crank-Nicolson方法在数值求解BSDE的过程中都需要求解非线性方程。无论使用哪种迭代方法,整个运算过程中都占用了大部分的运算时间,为提高运算效率,提出求解BSDE的预估校正方法。 首先,引入一个新的随机过程 (27) (28) 将式(28)作为新的参考方程,根据数值积分和预估校正的思想,给出求解BSDE的预估校正方法如下。 给定随机变量X0,YN,ZN,对n=N-1,…,1,0,可以通过下列方程组求解(Yn,Zn): 算法3 求解BSDE的预估校正方法 Input: tn,Xn,EtnYn+1 ,Etngn+1 ,EtnYn+1ΔBtn+1 ,Etngn+1ΔBtn+1 Output: Yn,Zn 1) function ALG. BSDE. PC(tn,Xn,E(tn,Xn)) 2) Zn←2Δtn+1EtnYn+1ΔBtn+1 +2Etngn+1ΔBtn+1 3) Yn←EtnYn+1 +ΔtnEtngn+1 4) Yn←EtnYn+1 +12Δtng(tn,Xn,Yn,Zn)+12ΔtnEtngn+1 5) return (Yn,Zn) 6) end function 使用上述3种数值方法,对计算g-VaR的BSDE(式(17))进行数值求解。 (28) 然后,分别取N=16、32、64、128和256,并分别使用Euler方法、Crank-Nicolson方法和预估校正方法对BSDE(式(29))进行求解,结果如表1所示。 表1 数值实验结果 建立基于g-期望的互联网理财产品风险度量模型,给出g-VaR的一般公式,并利用求解BSDE的数值方法进行数值计算,利用Euler格式、Crank-Nicolson格式以及预估校正方法进行了一般算法和实验分析,得出以下结论。 1)g-期望理论与VaR相结合可更好地解决互联网理财产品领域不确定性风险测度。利用一般g-期望探讨相容风险度量的有关问题,并结合VaR提出一种新的风险度量工具g-VaR模型,进而对特殊的生成元g给出g-VaR的数学定义,构造基于g-VaR的风险度量模型,在度量互联网理财产品的风险不确定性方面更具优势,能够更为准确地度量互联网理财产品所面临的风险。 2) 数值分析结果显示了g-VaR在衡量不确定性风险中的有效性,且预估校正方法结果较优。考虑到直接将实际数据代入理论模型中仍有较高难度,分别采用Euler方法、Crank-Nicolson方法以及预估校正方法等数值分析方法模拟g-VaR模型的应用效果。模拟过程显示:Euler方法和Crank-Nicolson方法在数值求解BSDE的过程中,都需要求解非线性方程且运算时间较长。而预估校正方法相对而言提升了整体运算效率,且计算精度的稳定性较好。 本研究仅从理论方面探讨了g-VaR模型在互联网理财产品中的应用,并用数值模拟的方法初步探索了该模型的应用情况。未来需利用互联网理财产品的实际数据来验证该理论模型的可行性。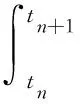
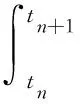
3.1 Euler方法

3.2 Crank-Nicolson方法
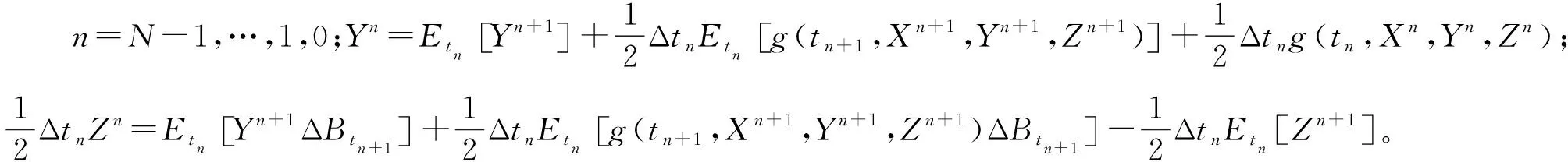


3.3 预估校正方法


3.4 数值实验

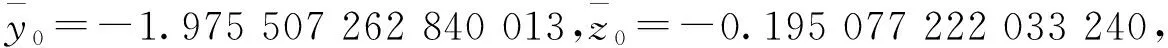

4 结论
