货运停车各方参与主体决策行为演化博弈分析

陈 丰 丁文龙 李军强 马小翔 张 平

(1 同济大学道路与交通工程教育部重点实验室，上海 201804)(2 同济大学经济与管理学院，上海 210092)(3 西南交通大学交通运输与物流学院，成都 611756)(4 西藏大学工学院，拉萨 850000)

货运交通是交通运输系统的重要组成部分.近年来，随着物流业的快速发展，货车数量持续增加，货运交通对整个交通系统的影响越来越大，由此产生的货运停车管理问题也亟需解决.

针对货运交通问题，国内外学者从不同角度对其展开了研究.Ibeas等[1]对城市货物运输中的数据收集和模型建立进行了研究.Ballantyne等[2]分析了不同背景下的城市货运问题，指出城市货运规划可以通过各方面相互合作来改进.Carrese等[3]研究了欧洲重型车辆(HGV)停车场设计中存在的问题.Nuzzolo等[4]提出了一种建模方法，以解决城市和货运相关的交通设施之间存在的相互关系.Straka等[5]研究了网络化货运停车策略的制定问题.Amer等[6]构建了一个以社会福利最大为目标的Con-cave分配模型，用于研究城市中心货车停车问题.

货运停车场选址及规划问题是近年来货运交通领域研究的一个热点问题.Dezi等[7]以货车最短行驶距离和最大服务能力为目标，利用最大覆盖选址模型对博洛尼亚市中心停车场规划问题进行了研究.Joao等[8]运用结构方程模型框架，分析了城市货运配送停车问题与商业设施特征、相关分销渠道、配送运营模式和当地土地利用模式之间的关系.Malik等[9]对瑞典哥德堡和印度德里的货运司机停车行为进行了对比分析.Aljohani等[10]研究了城市内部货运停车场选址问题，并建立了决策支持系统.

货运交通结构优化及货物运输中的安全问题也是国内外学者研究的重点.项昀等[11]分析了货运交通结构，研究了货运分担率问题.Caro等[12]分析了西班牙危险货物停车设施布局问题，借助地理信息系统建立了危险货物装载车停车场最大覆盖选址模型.Vela等[13]考虑危险货物对周边居民的影响，以集体负效应及社会风险最小为目标，建立了数据包络(DEA)的危险货物装载车停车场选址模型.张兰芳等[14]根据G15上海段的交通事故数据及交通流数据，建立了考虑货车影响的高速公路交通流风险预测模型.

对货运交通的研究主要集中在停车场选址、货运停车方法优化、货运交通结构优化以及危险品运输等方面，针对货运停车管理方面的研究相对欠缺.一般而言，货运停车管理中的主体包括政府管理部门、货运停车经营企业及货运司机，三者之间通常存在着博弈行为.通过演化博弈方法对三者的决策行为进行分析，是研究货运停车管理的有效方法之一.货运停车三方主体作为理性人，在货运停车管理当中会以自身收益最大为目标进行决策，任意一方或两方决策行为的变化都会引起剩余两方或一方决策行为发生改变.鉴于此，本文采用演化博弈理论研究货运停车管理中各参与主体决策行为，分析其对博弈结果造成的影响，从而为货运停车管理提供合理的对策建议.

1 问题描述与基本假设

货运停车场作为货车停放的主要场所，其服务水平的高低直接影响到货运司机的停车行为.如果货运停车场经营企业规范经营，提供的服务水平较高，停车收费标准较为合理，则更多的货运司机会选择到货运停车场停车；相反，如果货运停车场经营企业不规范经营，提供的服务水平较差，收费偏高，货运司机则会选择在路边或者其他地方进行停车，很多情况下还存在违规停车的现象，对道路交通的通行效率及交通安全都造成了严重影响.政府部门的管理在解决上述问题中发挥着至关重要的作用.针对本文研究内容，进行如下假设：

假设1各博弈主体行为独立.经营企业的选择策略为“规范经营”和“不规范经营”；货运司机的选择策略为“到货运停车场停车”和“拒绝到货运停车场停车”；政府部门的选择策略为“监管”和“不监管”.经营企业规范经营、货运司机到货运停车场停车和政府部门监管的概率分别用x、y、z表示，经营企业不规范经营、货运司机拒绝到货运停车场停车和政府部门不监管的概率则分别用1-x、1-y、1-z表示,且x,y,z∈[0,1].

假设2各博弈主体作为理性人，都以自己利益最大化为目标.一方策略发生改变时，其他参与主体会适时做出相应的调整.

2 动态博弈模型

政府部门对经营企业和货运司机选择监管，也可以选择不监管.2种情况下的收益结果见表1.表中，C1表示经营企业规范经营时产生的成本，包括人力、物力以及财力等方面的投入；C2表示货运司机选择到货运停车场停车产生的成本，如停车费、食宿费等；C3表示政府监管时产生的监管成本；R1、R2分别表示经营企业和货运司机的初始收益；R3表示政府监管时获得的总收益，包括政府形象提升、税收增加、交通事故减少、道路交通秩序得到良好维护以及社会福利提高所带来的收益等；ΔR1表示货运司机选择到货运停车场停车给停车场经营企业带来的收益增量；ΔR2表示经营企业规范经营给货运司机带来的收益增量；A1表示经营企业规范经营时政府对经营企业的财政补贴；A2表示货运司机将车停到停车场时政府给予货运司机的资金补贴；ΔL1表示货运司机选择到货运停车场停车，但是经营企业不规范经营，经过长期或多次博弈后给经营企业带来的损失；ΔL2表示经营企业规范经营，但是货运司机拒绝到停车场停车，经过长期或多次博弈后给货运司机带来的损失；α∈(0,1)表示政府不进行监管时的总收益占监管时总收益的比例；αR3表示政府选择不监管策略获得的收益.

表1 博弈主体收益结果

3 博弈均衡分析及复制动态方程

3.1 经营企业博弈均衡分析

根据表1，假定经营企业规范经营时的期望收益值为Ue1，不规范经营时的期望收益值为Ue2，平均期望收益为Ue.三者的计算式分别为

Ue1=yz(R1+ΔR1-C1+A1)+(1-y)z(R1-

C1+A1)+y(1-z)(R1+ΔR1-C1)+

(1-y)(1-z)(R1-C1)=R1-C1+

zA1+yΔR1

(1)

Ue2=yz(R1+ΔR1-ΔL1)+(1-y)zR1+

y(1-z)(R1+ΔR1-ΔL1)+(1-y)·

(1-z)R1=R1+y(ΔR1-ΔL1)

(2)

Ue=xUe1+(1-x)Ue2

(3)

3.2 货运司机博弈均衡分析

假定货运司机到货运停车场停车的期望收益为Ud1，拒绝到货运停车场停车的期望收益为Ud2，平均期望收益为Ud.三者的计算结果分别为

Ud1=xz(R2+ΔR2-C2+A2)+(1-x)z(R2-

C2+A2)+x(1-z)(R2+ΔR2-C2)+

(1-x)(1-z)(R2-C2)=R2-C2+

zA2+xΔR2

(4)

Ud2=xz(R2+ΔR2-ΔL2)+(1-x)zR2+

x(1-z)(R2+ΔR2-ΔL2)+(1-x)·

(1-z)R2=R2+x(ΔR2-ΔL2)

(5)

Ud=yUd1+(1-y)Ud2

(6)

3.3 政府部门博弈均衡分析

假定政府部门监管时的期望收益值为Ug1，不监管时的期望收益值为Ug2，平均期望收益值为Ug.由表1可得

Ug1=xy(R3-C3-A1-A2)+(1-x)y(R3-

C3-A2)+x(1-y)(R3-C3-A1)+

(1-x)(1-y)(R3-C3)=R3-C3-

xA1-yA2

(7)

Ug2=xyαR3+(1-x)yαR3+x(1-y)αR3+

(1-x)(1-y)αR3=αR3

(8)

Ug=zUg1+(1-z)Ug2

(9)

3.4 复制动态方程

根据式(1)和(2)，可得经营企业的复制动态方程为

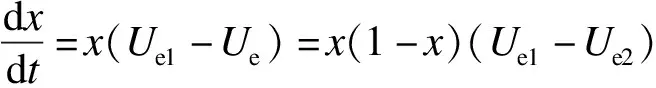
x(1-x)(-C1+zA1+yΔL1)

(10)

根据式(4)和(5)，可得货运司机的复制动态方程为

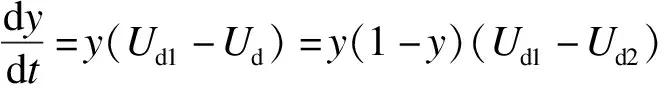
(11)

根据式(7)和(8)，可得政府部门的复制动态方程为

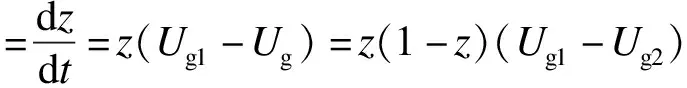
z(1-z)[(1-α)R3-C3-xA1-yA2]

(12)

4 演化稳定策略分析

4.1 经营企业演化稳定策略分析

根据式(10)的计算结果，令

(13)

当z=z0时，F(x)≡0，表示无论经营企业选择规范经营的概率如何变化，都不会对博弈的结果产生影响，演化博弈结果都将处于一种稳定状态.

当z≠z0时，令F(x)=0.通过经营企业的复制动态方程可以得到2个稳定点：x=0和x=1.对经营企业的复制动态方程进行求导可得

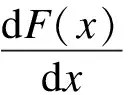
(14)

根据微分方程稳定性定理可知，如果经营企业采取的某一策略为稳定策略，则必须满足以下条件成立：

(15)

经营企业的复制动态相位图见图1.图中阴影部分将空间分为Ⅰ(阴影部分前面)和Ⅱ(阴影部分后面)两部分.当经营企业的初始状态处于空间Ⅰ时，稳定点为x=1，表示经营企业最终会选择规范经营；当经营企业的初始状态处于空间Ⅱ时，稳定点为x=0，表示经营企业最终会选择不规范经营.

除了定、转子铁心冲片的拼缝之外，冲片上的开孔、冲片的定位槽也遵循上述规律，只需把(1)式中总拼缝数n×t理解为圆周均布的开孔数和定位槽数即可。

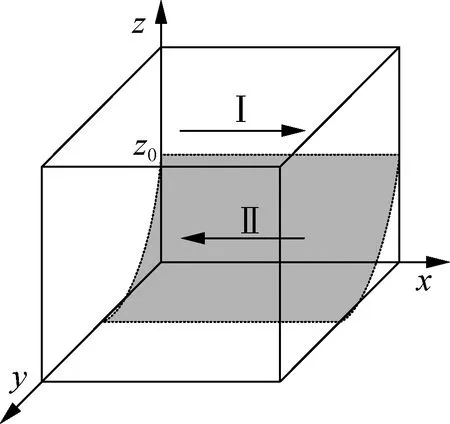
图1 经营企业复制动态相位图

当A1增加时，对应z0减小，空间Ⅰ变大，空间Ⅱ变小，说明政府对经营企业的补贴增加会使经营企业规范经营的积极性增加.当ΔL1增加时，对应z0减小，空间Ⅰ变大，空间Ⅱ变小，说明如果经营企业不规范经营时的损失增加，会促使经营企业选择规范经营.当C1增加时，对应z0增加，空间Ⅰ变小，空间Ⅱ变大，说明如果经营企业规范经营时的成本不断增加，则经营企业更加倾向于选择不规范经营.当y增加时，对应z0减小，空间Ⅰ变大，空间Ⅱ变小，说明如果货运司机倾向于将车停到货运停车场，则经营企业会选择规范经营来提高服务水平，从而提高企业收益.

4.2 货运司机演化稳定策略分析

根据式(11)的计算结果，令

(16)

当x=x0时，F(y)≡0，表示无论货运司机选择到货运停车场停车的概率如何变化，都不会对博弈的结果产生影响，演化博弈结果都将处于一种稳定状态.

当x≠x0时，令F(y)=0.通过货运司机的复制动态方程可以得到2个稳定点：y=0和y=1.对货运司机的复制动态方程进行求导可得

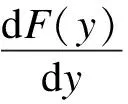
(17)

根据微分方程稳定性定理可知，如果货运司机采取的某一策略为稳定策略，则必须满足以下条件成立：

(18)

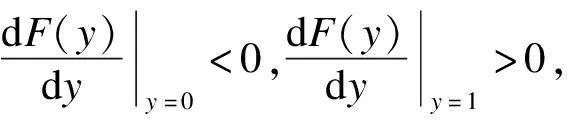
货运司机的复制动态相位图见图2.图中阴影部分将空间分为Ⅲ(阴影部分右侧)和Ⅳ(阴影部分左侧)两部分.当货运司机的初始状态处于空间Ⅲ时，稳定点为y=1，表示货运司机最终会选择到货运停车场停车；当经营企业的初始状态处于空间Ⅳ时，稳定点为y=0，表示货运司机最终会选择不到货运停车场停车.

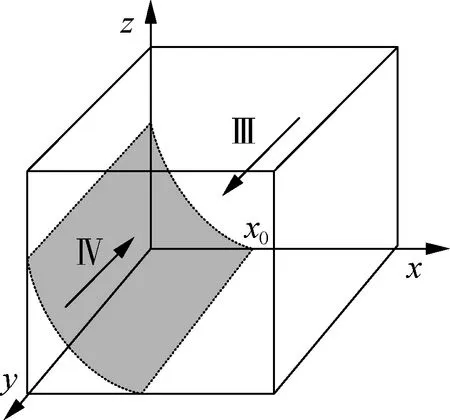
图2 货运司机复制动态相位图

当A2增加时，对应x0减小，空间Ⅲ变大，空间Ⅳ变小，说明政府对货运司机的资金补贴增加时，货运司机选择到货运停车场停车的积极性增加.当ΔL2增加时，对应x0减小，空间Ⅲ变大，空间Ⅳ变小，说明如果货运司机拒绝到停车场停车的损失增加，则会促使货运司机选择到货运停车场停车.当C2增加时，对应x0增加，空间Ⅲ变小，空间Ⅳ变大；说明如果货运司机到货运停车场停车所花费的成本不断增加，会促使货运司机选择不到货运停车场停车.当z增加时，对应x0减小，空间Ⅲ变大，空间Ⅳ变小，说明如果政府部门强化监管力度，则货运司机到货运停车场停车的意愿会增加.

通常情况下，政府管理部门对经营企业和货车司机的管理难度不同.与货运司机相比，企业通常更容易管理.通过分析可知，货运停车场停车成本增加是导致货运司机选择拒绝到货运停车场停车的原因之一.如果政府管理部门强化对经营企业的管理，加强对经营企业收费及服务水平的监督，控制好经营企业的收费标准，则会增加货运司机到停车场停车的收益.此时，更多的货运司机则会选择到货运停车场停车，货运停车不规范问题将会得到有效解决.如果政府部门强化对货运司机的监管力度，则货运司机也会改变自己的停车意愿，选择到货运停车场停车.然而，货运司机数量较为庞大，政府管理部门对其进行管理时投入的成本会很大.另一方面，政府管理部门强化对货运司机的监管力度并不能提高货运司机到停车场停车的实际收益.长期来看，加大对经营企业的管理相比于加大对货运司机的管理成本更低，难度更小，货运停车不规范问题也更容易解决.

4.3 政府部门演化稳定策略分析

根据式(12)的计算结果，令

(19)

当y=y0时，F(z)≡0，表示无论政府部门选择监管的概率如何变化，都不会对博弈的结果产生影响，演化博弈结果都将处于一种稳定状态.

当y≠y0时，令F(z)=0.通过政府部门的复制动态方程可以得到2个稳定点：z=0和z=1.对政府部门的复制动态方程进行求导可得

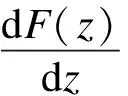
(20)

根据微分方程稳定性定理可知，如果政府部门采取的某一策略为稳定策略，则必须满足以下条件：

(21)

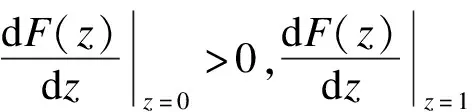
政府部门的复制动态相位图见图3.图中阴影部分将空间分为Ⅴ(阴影部分后面)和Ⅵ(阴影部分前面)两部分.当政府部门的初始状态处于空间Ⅴ时，稳定点为z=1，表示政府部门最终会选择监管；当政府部门的初始状态处于空间Ⅵ时，稳定点为z=0，表示政府部门最终会选择不监管.

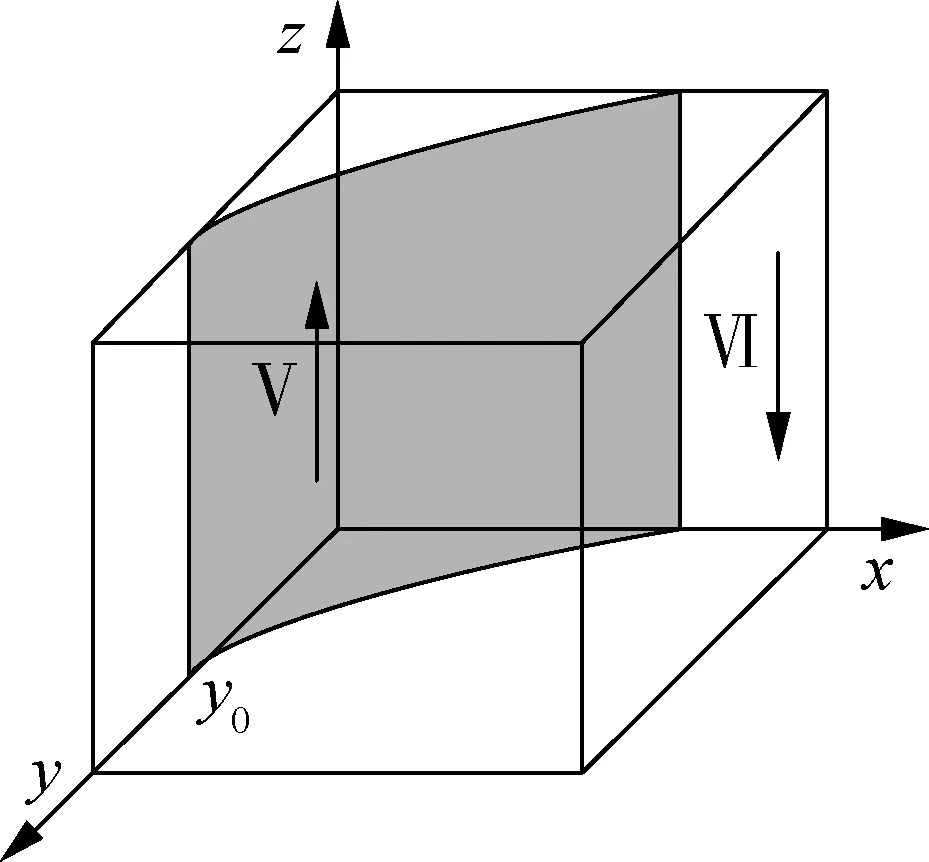
图3 政府部门复制动态相位图

当A1、A2增加时，对应y0减小，空间Ⅵ变大，空间Ⅴ变小，说明政府对经营企业和货运司机的补贴不断增加时会促使政府逐步倾向于选择不监管.当R3增加时，对应y0增加，空间Ⅴ变大，空间Ⅵ变小，说明如果政府部门监管情况下政府的收益不断增加，政府部门会更加倾向于选择监管.当C3增加时，对应y0减小，空间Ⅵ变大，空间Ⅴ变小，说明如果政府部门监管情况下的监管成本不断增加，则政府部门会逐步倾向于选择不监管.当x增加时，对应y0减小，空间Ⅵ变大，空间Ⅴ变小，说明如果经营企业选择规范经营，则政府会倾向于选择不监管.

5 数值分析

根据第3节中经营企业、货运司机、政府部门的演化博弈模型，借助于Matlab软件，结合各方参与主体的复制动态方程，通过数值仿真对演化博弈过程及结果进行分析.在对混合博弈问题进行研究时，根据相关研究领域专家的意见对参数进行初始化设置是研究过程中常用的方法[15].本文在实际调研的基础上，邀请了8位行业专家对参数初始化值进行定量化处理.处理方法为结合各专家的观点，先设定各参数的范围；然后，各专家在规定范围内给出各参数的初始值；最后，将8位专家给出的初始值求平均数，结果见表2.

表2 参数定量化统计表

5.1 政府补贴政策的影响

对开始阶段经营企业不倾向于规范经营，货运司机不倾向于到货运停车场停车，政府管理部门监管力度很强的情况进行仿真，结果见图4.图中，p为概率；t为时间步长.由图可知，政府管理部门在初始阶段监管的力度很大(z=0.99).由于经营企业规范经营的意愿不强，货运司机到货运停车场停车的收益不能增加，故货运司机倾向于不到货运停车场停车，使得经营企业的收益也不能增加，继而导致经营企业不倾向于规范经营.虽然管理部门的监管力度很大，但是博弈过程中经营企业和货运司机的收益都较低，最终博弈三方的策略向(0,0,1)演化.如果政府管理部门想要改变演化博弈的结果，提高经营企业或货运司机的收益是解决问题的有效途径.

图4给出了政府管理部门对货运司机资金补贴A2=120时的仿真结果.对货运司机补贴增加后的博弈过程进行仿真，结合各位专家的建议，资金补贴由120提高到140，此时的演化博弈仿真结果见图5.由图可知，当政府管理部门增加货运司机补贴后，货运司机开始倾向于到货运停车场停车，从而增加了经营企业的收益，使得经营企业也倾向于规范经营，但其选择行为的改变滞后于货运司机，博弈结果向(1,1,1)演化.

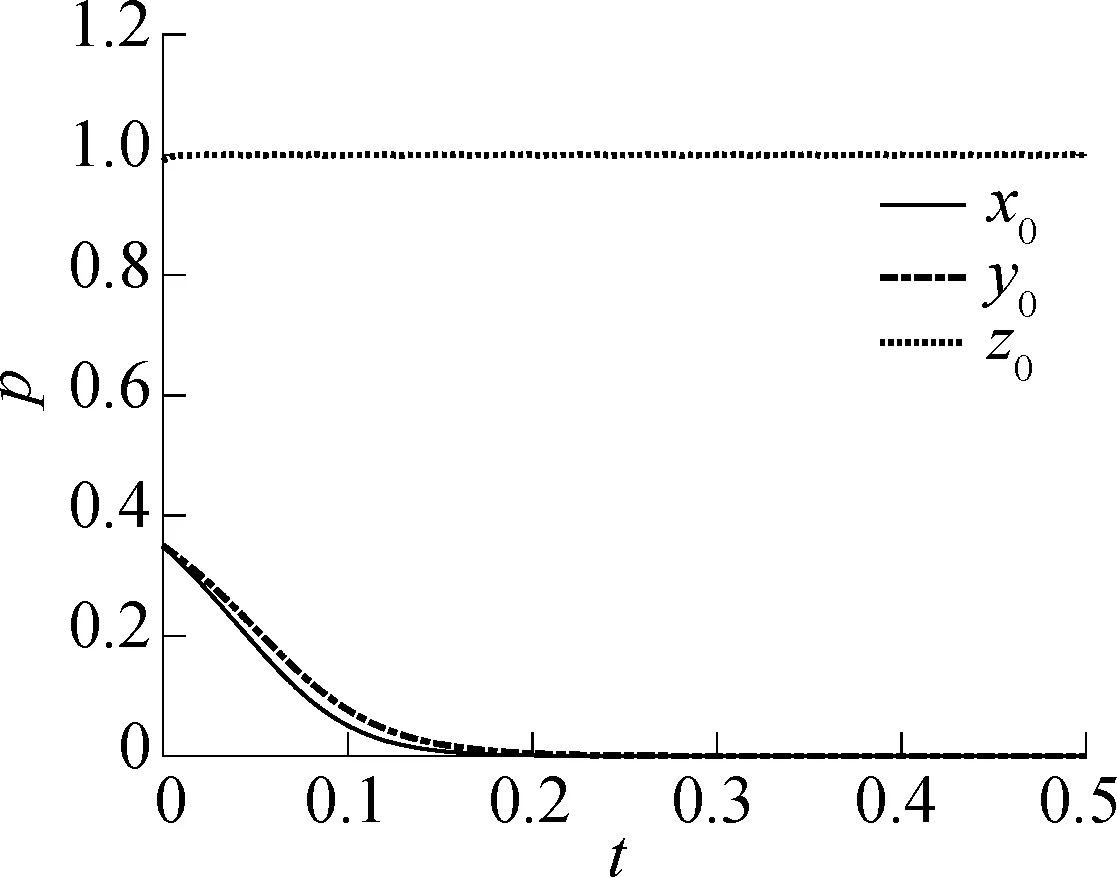
(a)x0=0.35,y0=0.35,z0=0.99

针对政府管理部门对货运司机的资金补贴进行进一步分析，A2=140时的仿真结果见图5.当x0=0.35,y0=0.35,z0=0.99,A2=138时，仿真结果见图6(a).由图可知，当A2=138时，各博弈主体的决策不能向(1,1,1)演化.

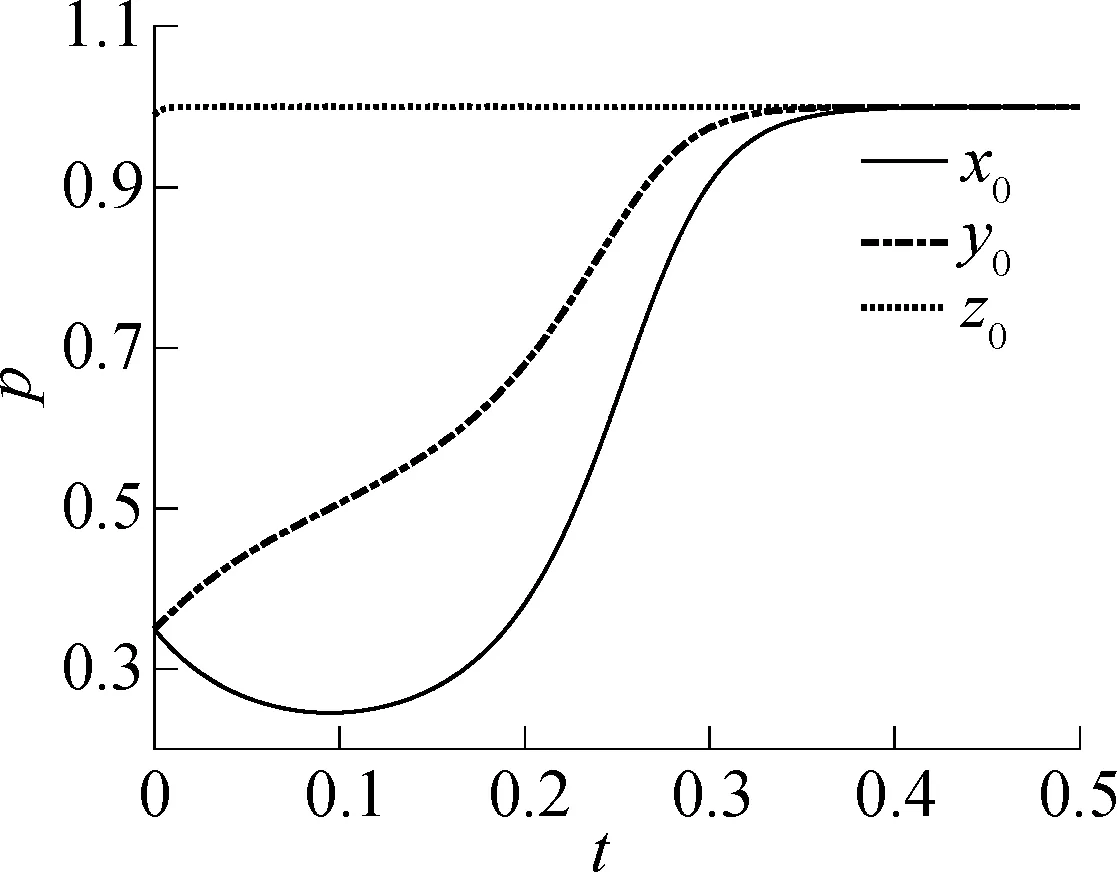
(a)x0=0.35,y0=0.35,z0=0.99

当A2=139时，演化博弈的仿真结果见图6(b).对比图6(a)和(b)发现，当货运司机资金补贴由138增加到139时，可使各个博弈主体的决策向(1,1,1)演化.因此，政府对货运司机最经济的补贴为139.

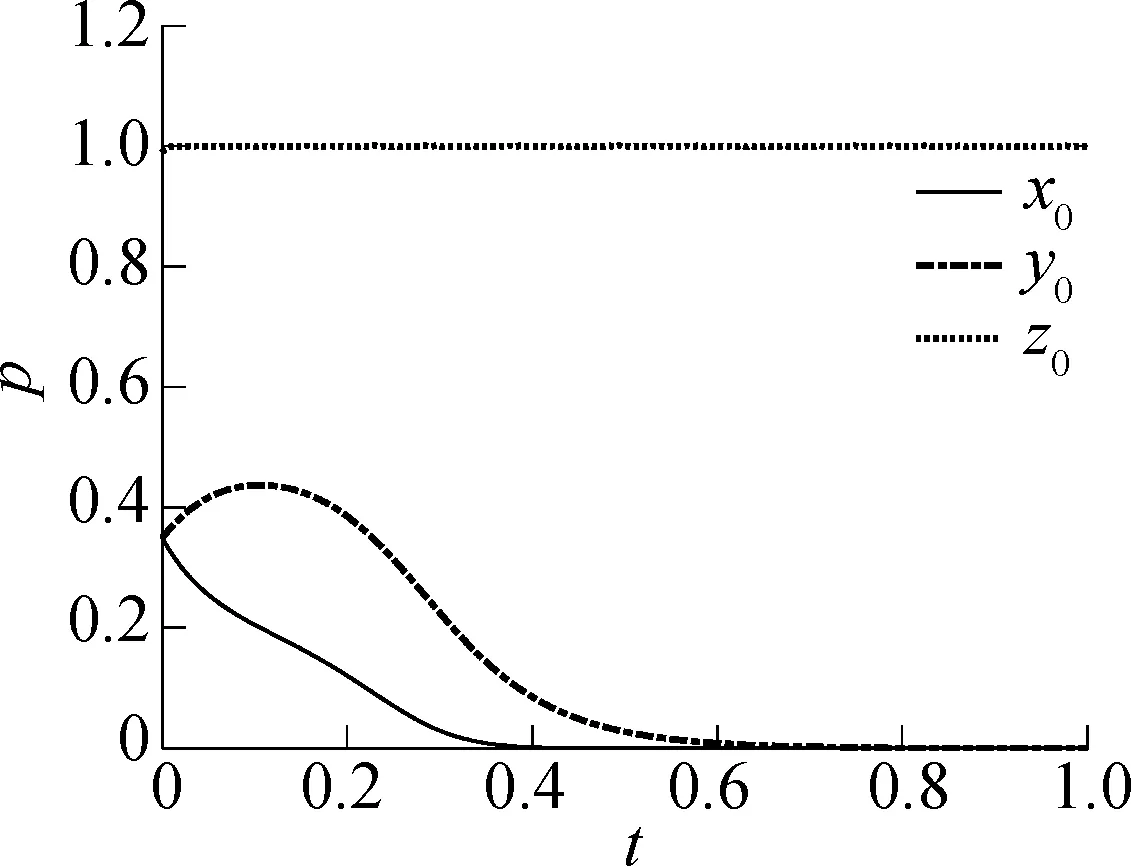
(a)A2=138,x0=0.35,y0=0.35,z0=0.99

如果政府对货运司机的补贴力度不发生改变(A2=120)，而是增加对经营企业的补贴，由A1=160变为A1=200，演化博弈仿真结果见图7.由图可知，经营企业开始时为了节省资金，倾向于选择不规范经营.但是当政府管理部门对经营企业规范经营情况下的补贴增加后，经营企业则会选择规范经营，相应增加了货运司机到货运停车场停车的收益，使得货运司机更加倾向于到货运停车场停车.因此政府管理部门增加对经营企业的资金补贴是实现各方共赢、规制货运停车不规范现象的有效途径之一.

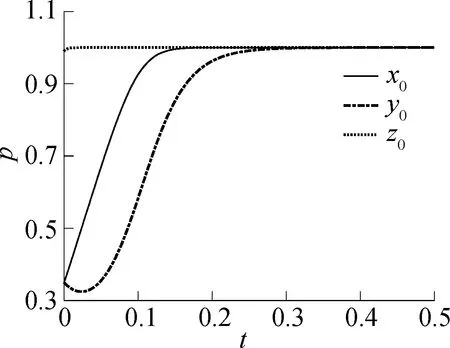
(a)x0=0.35,y0=0.35,z0=0.99

针对政府管理部门对经营企业的资金补贴进行进一步分析.当x0=0.35,y0=0.35,z0=0.99,A1=181时，仿真结果见图8(a).由图可知，当A1=181时，各博弈主体的决策不能向(1,1,1)演化.当A1=182时，演化博弈的仿真结果见图8(b).对比图8(a)和(b)可知，当经营企业资金补贴由181增加到182时，各博弈主体的决策将会向(1,1,1)演化.因此，政府对经营企业的最佳补贴为182.

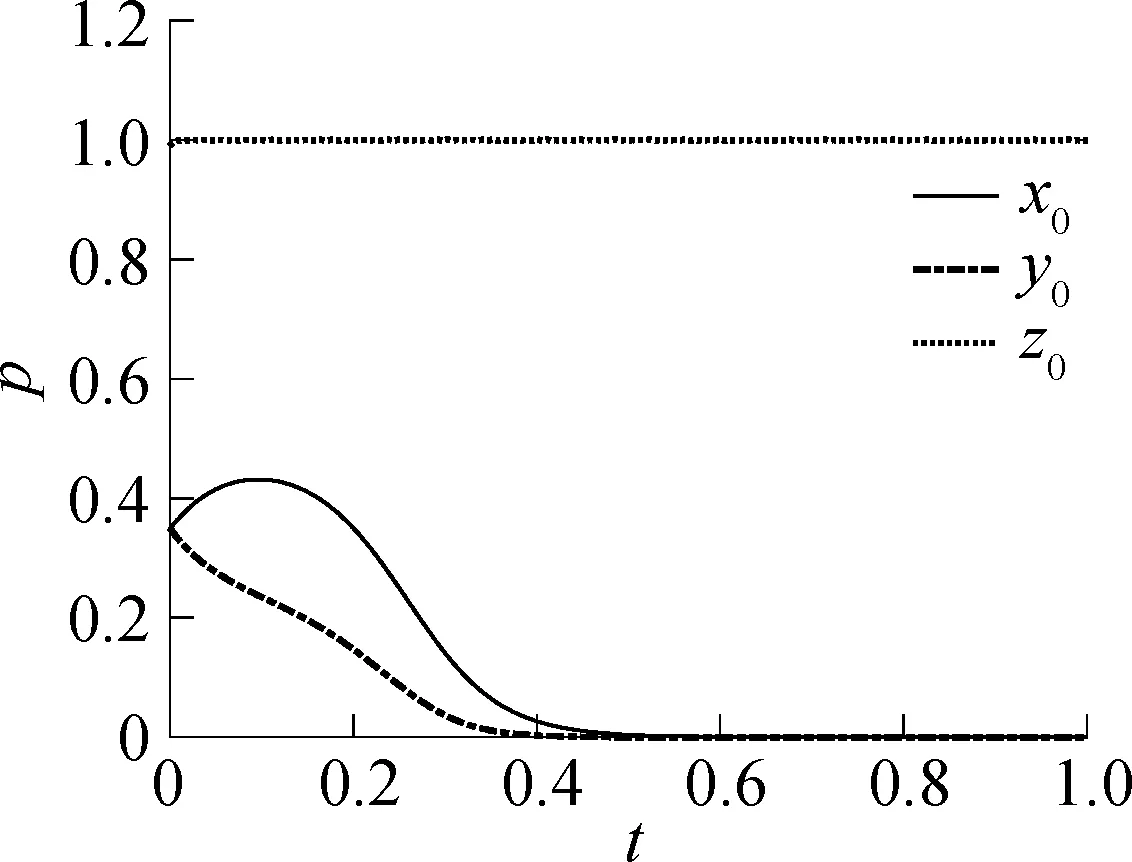
(a)A1=181,x0=0.35,y0=0.35,z0=0.99

5.2 政府部门监管力度的影响

实际中，政府监管力度的改变会影响经营企业和货运司机的决策行为.假设政府部门对经营企业的补贴A1=160，对货运司机的补贴A2=140.政府部门监管力度改变时的仿真结果见图9.

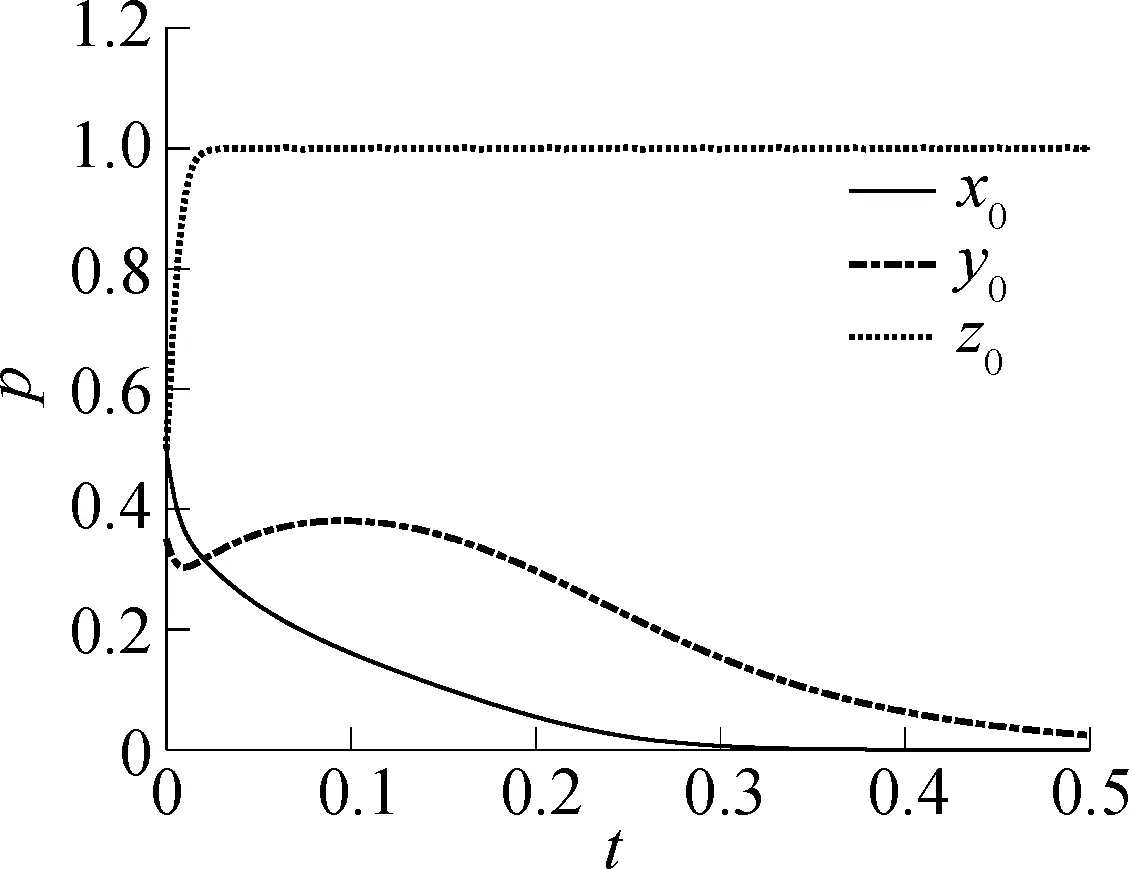
(a)x0=0.50,y0=0.35,z0=0.50

由图9可知，当政府管理部门的监管力度不强(z=0.50)时，博弈三方的策略向(0,0,1)演化，货运司机选择不到货运停车场停车，经营企业也选择不规范经营.当政府监管力度逐渐增强时，博弈结果演化为(1,1,1).政府管理部门监管的力度越大，货运司机就会越早选择到货运停车场停车，经营企业也会越早地选择规范经营，演化为(1,1,1)的速度越快.

5.3 监管成本的影响

实际中，政府管理部门在对经营企业和货运司机进行监管时需要一定成本，但是成本并不固定.如果监管成本减少，管理部门的收益就会增加，此时管理部门更倾向于进行监管；如果监管成本增加，管理部门的收益则会相应减少.假如开始阶段经营企业、货运司机的参与意愿都较强(x=0.65,y=0.65)，管理部门的监管力度较大(z=0.99)，监管成本增加(C3由100增加到200)时，演化博弈仿真结果见图10.仿真过程中政府管理部门对经营企业的补贴A1=160，对货运司机的补贴A2=140.

由图10可知，当C3=200时，政府管理部门的监管成本增加.在博弈开始阶段，由于监管部门监管力度很大，经营企业和货运司机分别选择规范经营和到货运停车场停车，三方决策向(1,1,1)演化.随着监管成本的增加，在三方策略演化为(1,1,1)后，管理部门为了节约监管成本，逐步倾向于不进行监管；经营企业为了节省经营成本，也逐步倾向于选择不规范经营，使得货运司机到货运停车场的收益降低，导致货运司机选择不到货运停车场停车.从而对道路的通行能力和交通安全造成影响，继而迫使政府管理部门又加强了监管，经营企业、货运司机和管理部门的策略又重新演化为(1,1,1).此后，管理部门为了节省监管成本，倾向于不进行监管，经营企业开始选择不规范经营，货运司机也倾向于不到货运停车场停车，致使x、y变得很小(接近0)；为了缓解货运停车不规范行为带来的负面影响，管理部门又重新加强了监管力度，但是由于经营企业和货运司机的参与力度太低，因此混合博弈的结果不能重新演化为(1,1,1).

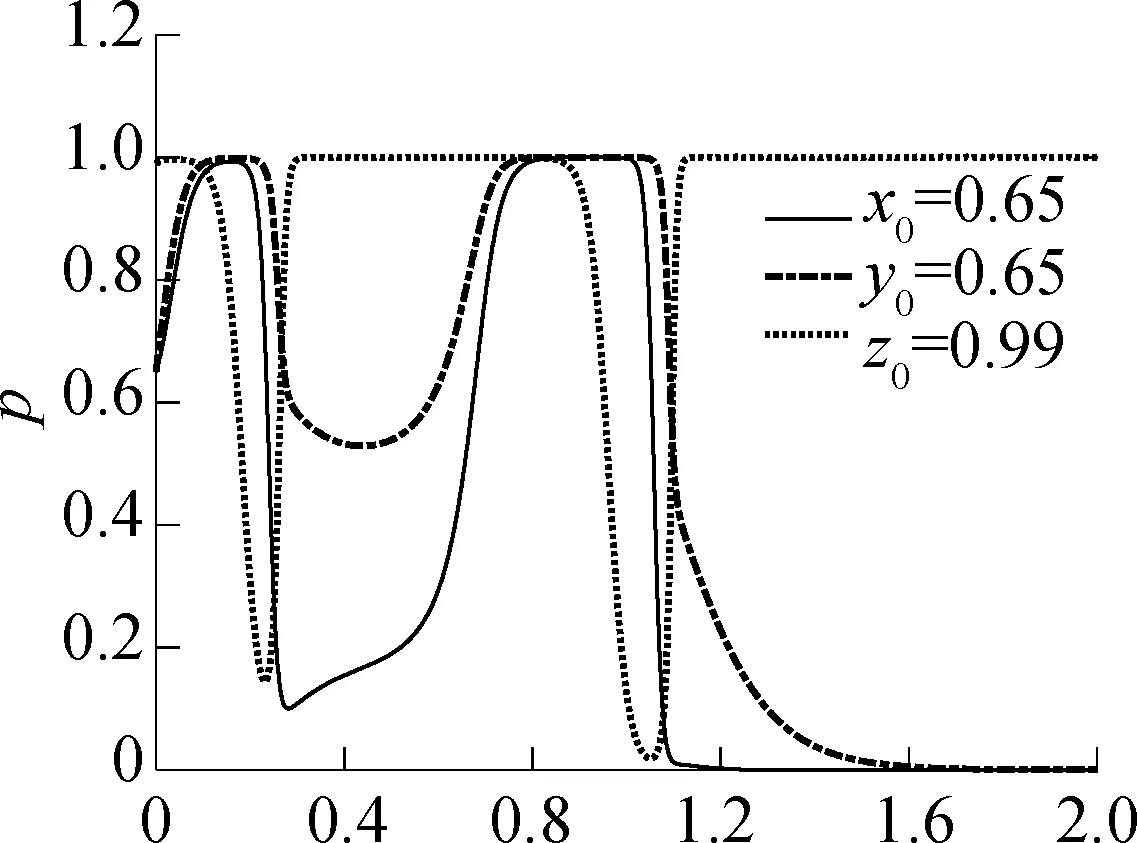
图10 监管成本增加后仿真结果

5.4 经营企业参与意愿的影响

假设政府管理部门对经营企业和货运司机的补贴分别为A1=200,A2=120，经营企业参与意愿变化仿真结果见图11.由图可知，在政府监管力度和货运司机到停车场停车意愿不变的情况下，经营企业规范经营的意愿越强，越容易使三方的决策演化为(1,1,1).究其原因在于，政府管理部门加大对经营企业规范经营的补贴后，如果经营企业选择规范经营，那么其收益就会增加.经营企业越早进行规范经营，货运司机就会越早选择到货运停车场停车.

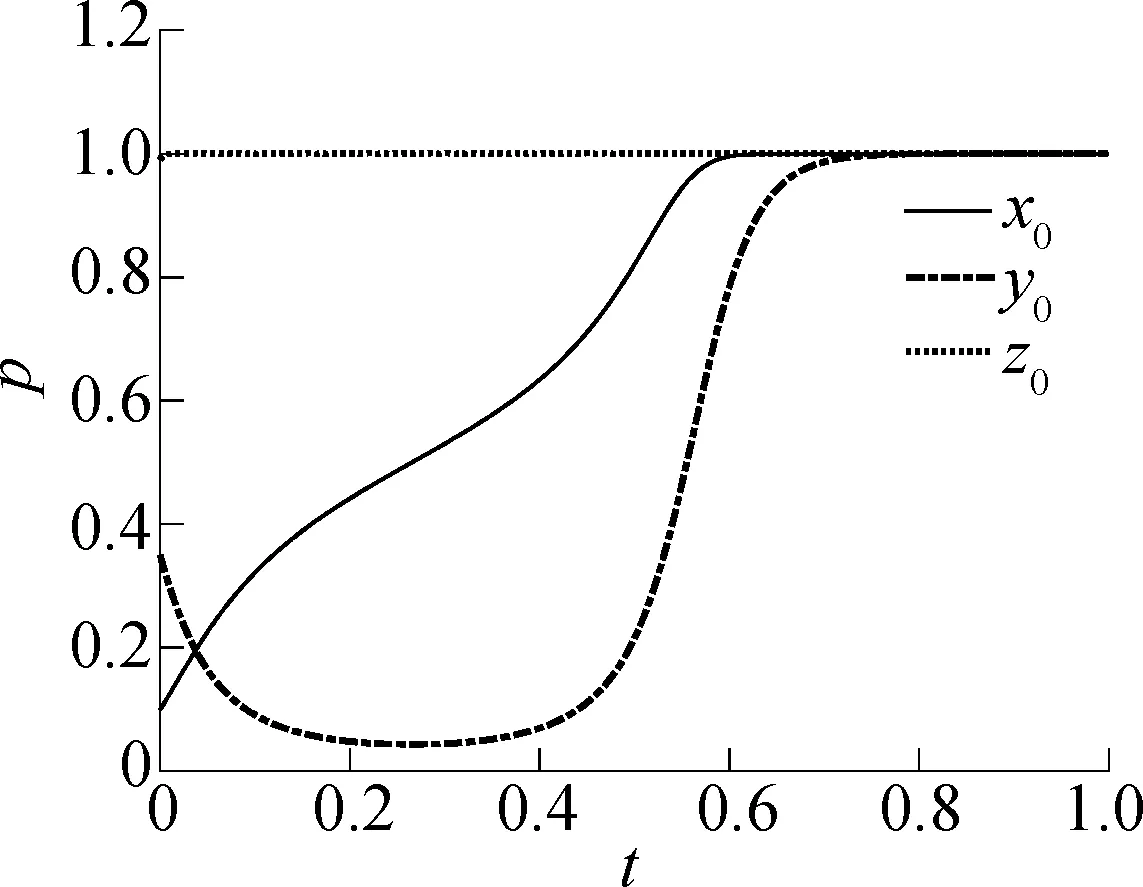
(a)x0=0.10,y0=0.35,z0=0.99

5.5 货运司机参与意愿的影响

假设政府管理部门对经营企业和货运司机的补贴分别为A1=160,A2=140，货运司机参与意愿变化的仿真结果见图12.由图可知，当y=0.10时，经营企业、货运司机与政府管理部门的策略向(0,0,1)演化；当y=0.40和0.85时，经营企业、货运司机与政府管理部门的策略向(1,1,1)演化.引起变化的原因是，当y=0.1时，货运司机到货运停车场停车的意愿很低，使得经营企业的收益较少，导致经营企业倾向于选择不规范经营；当货运司机逐步到货运停车场停车时，经营企业的收益增加，使得其倾向于选择规范经营.

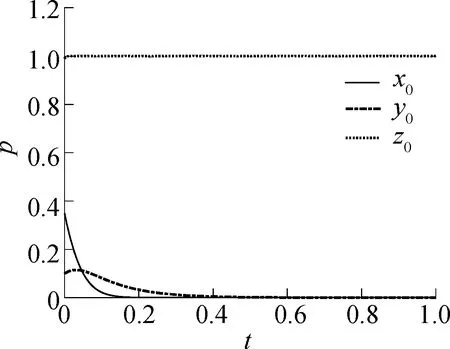
(a)x0=0.35,y0=0.10,z0=0.99

6 结论

1)本文通过演化博弈方法对货运停车博弈主体经营企业、货运司机、政府管理部门的决策行为进行了演化分析，系统研究了经营企业、货运司机、政府管理部门的演化博弈过程，并通过数值实验对演化博弈过程中的复制动态方程进行了仿真.

2)在经营企业和货运司机参与意愿都较低的情况下，政府管理部门应加大对经营企业或货运司机的经济补贴.经营企业或货运司机一方收益增加后，其参与意愿增加，决策行为也会相应改变.一方决策行为改变促使另外一方收益增加，导致决策行为也发生相应改变.混合博弈最终演化为(1,1,1)，货运停车不规范行为得到有效治理.

3)政府管理部门的监管力度在货运停车管理中起着重要作用.监管力度越强，经营企业越倾向于规范经营，货运司机也越倾向于到货运停车场停车，混合博弈结果越容易演化为(1,1,1)，停车不规范问题越容易得到治理.

4)监管成本增加后，政府部门不应该减弱监管力度.因为在监管力度减小后，混合博弈容易演化为(0,0,1).管理部门想要使混合博弈重新演化为(1,1,1)，就必须增加对经营企业或货运司机的经济补贴，导致管理成本增加.

5)政府管理部门对经营企业或货运司机的补贴增加到预期值后，经营企业和货运司机都应尽快改变自己的决策行为，从而增加了各方的收益.

6)本文通过演化博弈的方法对货运停车管理问题进行了研究.研究过程中着重分析了政府管理部门监管力度、资金投入以及经营企业和货运司机参与意愿等因素对博弈结果造成的影响.根据实际情况对模型进行修正以应用于更多的工程实践中，将是未来研究的重点内容.