基于可靠度理论考虑验证荷载的既有桥梁评估分项系数研究

2022-04-18徐望喜钱永久金聪鹤黄俊豪

东南大学学报（自然科学版） 2022年2期

徐望喜钱永久张方金聪鹤黄俊豪

(西南交通大学土木工程学院，成都 610031)

截至2019年底，我国公路桥梁总数达到 87.83万座，每年新竣工的公路桥梁数量也以近2万座的数量快速增长[1].随着桥梁服役年限的不断增加以及运营荷载的日益增长，大批既有桥梁出现超负荷运营、承载能力不足等现象[2].如何科学地对既有桥梁结构进行安全评估，充分发挥桥梁潜在承载能力是当前工程界和学术界紧迫任务之一.

以可靠度理论为基础对既有桥梁结构进行可靠性评估的研究主要可分为结构时变失效概率计算与评估分项系数计算2个方面.

Mori等[3]给出了荷载平稳随机过程与结构抗力劣化过程的时变可靠度计算公式，这些公式得到了广泛应用[4-5].在平稳随机过程模型基础上，Wang等[6]针对汽车荷载效应存在明显的逐年增加趋势而不再服从同一分布的特点，提出了考虑非平稳车载过程在役桥梁时变可靠度计算方法.Yuan等[7]采用时域离散与概率联合的方法来表征车载非平稳随机过程，结合抗力Gamma随机劣化过程构建既有混凝土桥梁的时变可靠度计算模型.以上研究所获取的可靠度计算结果虽能对结构风险进行量化分析，但由于计算复杂不利于实际工程实时应用.另一方面，与结构设计相比，既有结构可靠性评估的最大区别在于目标可靠度、荷载变量分布以及评估分项系数的取值等方面.侯天宇等[8]根据边际救生成本准则下的ALARP模式确定了既有混凝土桥梁安全性评估的目标可靠度.Yuan等[7]基于《公路桥梁承载能力检测评定规程》(JTG/T J21—2011)中混凝土桥梁评估理念与方法对既有桥梁结构提出了同时考虑目标可靠度、评估基准期因素影响下的两层次安全评估框架.

在上述研究基础上，以评估基准期与目标可靠度为变量的评估分项系数求解方法被提出.既有桥梁结构承受的历史服役荷载为结构抗力分布更新提供了有利信息，但在实际工程中往往受到忽视，导致对桥梁结构抗力认识不足.本文以可靠度理论为基础，构建在役桥梁评估理论基本框架，运用贝叶斯更新理论提出了综合考虑评估基准期与历史服役荷载的评估分项系数取值计算方法.并探讨了不同评估基准期以及历史服役验证期下评估分项系数的取值.最后通过某一典型简支T型梁桥进行运营安全指标分析，论证了评估系数取值的适用性.

1 评估理念与目标可靠度选取

1.1 评估理论框架

桥涵构件的承载能力极限状态可采用下式计算[9]:

(1)

式中，γ0为结构重要性系数；γGi为第i个永久作用的分项系数；SGi为第i个永久作用标准值；n为永久荷载类别个数；γQ为汽车荷载分项系数；SQk为汽车荷载标准值；R(·)为结构的抗力函数.

为便于判定结构安全性能，引入如下安全性能指标η：

(2)

式中，R0为结构名义抗力值；φ为抗力劣化系数；γ′R为抗力评估分项系数；γ′Gi、γ′Q分别为恒载和活载评估分项系数；S′Gi、S′Qk分别为实际恒载与实际车载的荷载效应评估标准值；μ为汽车冲击系数.当η∈(0,1]时，结构处于安全运营状态，可维持当前交通现状.当η∈(1,∞)时，结构不满足当前评估要求，需进一步进行评定，如进行现场荷载试验或对桥梁进行加固、限载通行等.

既有桥梁结构的安全性能指标与结构的名义抗力、评估分项系数、劣化系数以及荷载作用效应有关.其中，既有结构抗力劣化过程是与结构施工控制质量、服役环境、服役年限、混凝土碳化程度、钢筋锈蚀速率等因素有关的随机过程，难以获取精确的衰减模型，常采用某一确定性劣化函数来表示结构劣化过程.假定在基准期内荷载效应概率分布一致，在给定评估基准期的条件下，荷载效应模型也相应得到确定.因此评估分项系数γ′R、γ′Gi、γ′Q的取值成为本文研究的主要问题.

1.2 目标可靠度选取

欧洲规范EN1990—2002给出了任意基准期tref对应的目标可靠度βref与年目标可靠度β1a之间的换算关系，公式如下：

(3)

式中，Φ为标准化正态分布函数.

通过式(3)可获取基准期与目标可靠度的对应关系.文献[9]基于边际救生成本准则(MLSC)综合考虑个体风险(IRC)、社会风险(SRC)、生命质量指标(LQI)以及经济最优化原则(COP)确定在役桥梁的运营阶段目标可靠度.本文参考这一方法计算基准期为10、20、30、40 a 的目标可靠度，结果如表1所示.由于研究对象为梁桥，属于延性破坏控制，对应的一、二、三级安全等级可靠度分别为4.7、4.2、3.7.

表1 不同基准期下目标可靠度取值

2 基本变量统计参数及概率分布

假定结构抗力随机变量为R，恒载效应和活载效应随机变量分别为SG和SQ，那么结构功能函数可表示为

Z=R-SG-SQ

(4)

设计基准期内对应的统计参数如表2所示[10].根据式(4)可知给定目标可靠度、荷载效应分布类型以及荷载效应分布参数，可确定已知分布下的抗力模型参数.

表2 变量统计参数及概率分布

假定结构抗力、恒载效应模型在不同评估基准期内不变，荷载效应分布类型也不变，则不同基准期的荷载效应分布可通过下式计算：

FST(x)=[FS(x)]m

(5)

式中，FS(x)为单位基准期内荷载效应概率分布；FST(x)为基准期m内的荷载极值分布.计算结果如表3所示.

表3 不同基准期下荷载参数

3 抗力模型的贝叶斯更新

对于既有桥梁结构，历史服役荷载是结构抗力的有效验证(桥梁抗力大于所有已承受荷载).假定结构初始抗力的密度概率函数为fR(r),其中r为抗力的随机变量.通过荷载调查分析得到桥梁服役荷载分布函数为FS(·)，根据贝叶斯更新理论可得修正后的结构抗力密度概率函数f′R(r)为[11]

(6)

抗力更新后抗力的均值与方差分别为

(7)

(8)

假定抗力恒载标准值为SG=100，令SQk=αSG为汽车活载标准值.定义验证荷载效应标准值SP与活载效应标准值SQk比(简称验活比)λ=SP/SQk.

分别取活恒比α=0.5，1.0，1.5，2.0；验活比λ以0.2为步长，在0.8～3.0之间依次选取.各变量模型分布参数取值见表2，根据式(7)、(8)得出不同验活比λ下抗力更新后与更新前的均值比μ0/μ与标准差比σ0/σ，如图1和图2所示.

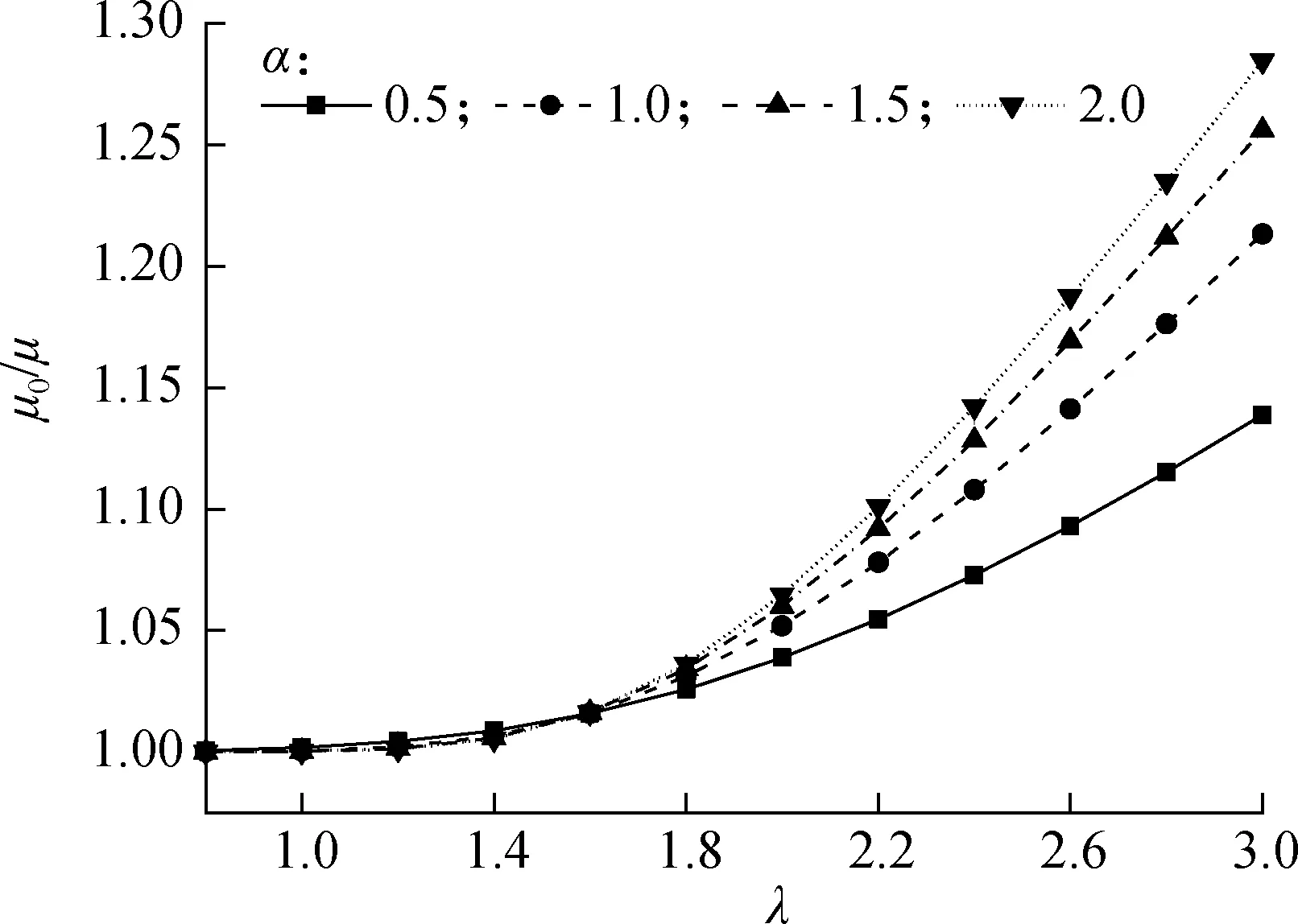
图1 不同验活比下抗力更新前后均值比

图2 不同验活比下抗力更新前后标准差比

随着验活比λ增加，抗力均值比逐步增大，标准差比逐步缩小.当活恒比α较大时，这一现象更加明显.以验活比λ=2.0为例，更新后抗力均值比由1.04(α=0.5)增加至1.06(α=2.0)，抗力标准差比由0.86(α=0.5)缩减至0.82(α=2.0).

为进一步探讨恒载取值对抗力分布更新的影响，选取S′G=γSG(γ=0.5，1.0，1.5，2.0，2.5)为恒载标准值.验活比取λ=1.0，活恒比α以0.1为步长，在0.5～2.0之间依次选取.根据式(7)、(8)计算更新前后抗力的均值与标准差，结果如图3和图4所示.在不同恒载水平γ条件下，4条曲线的变化趋势基本一致，说明在验证荷载作用下抗力更新效果与结构恒载的具体取值无关，与活恒比α、验活比λ有关.

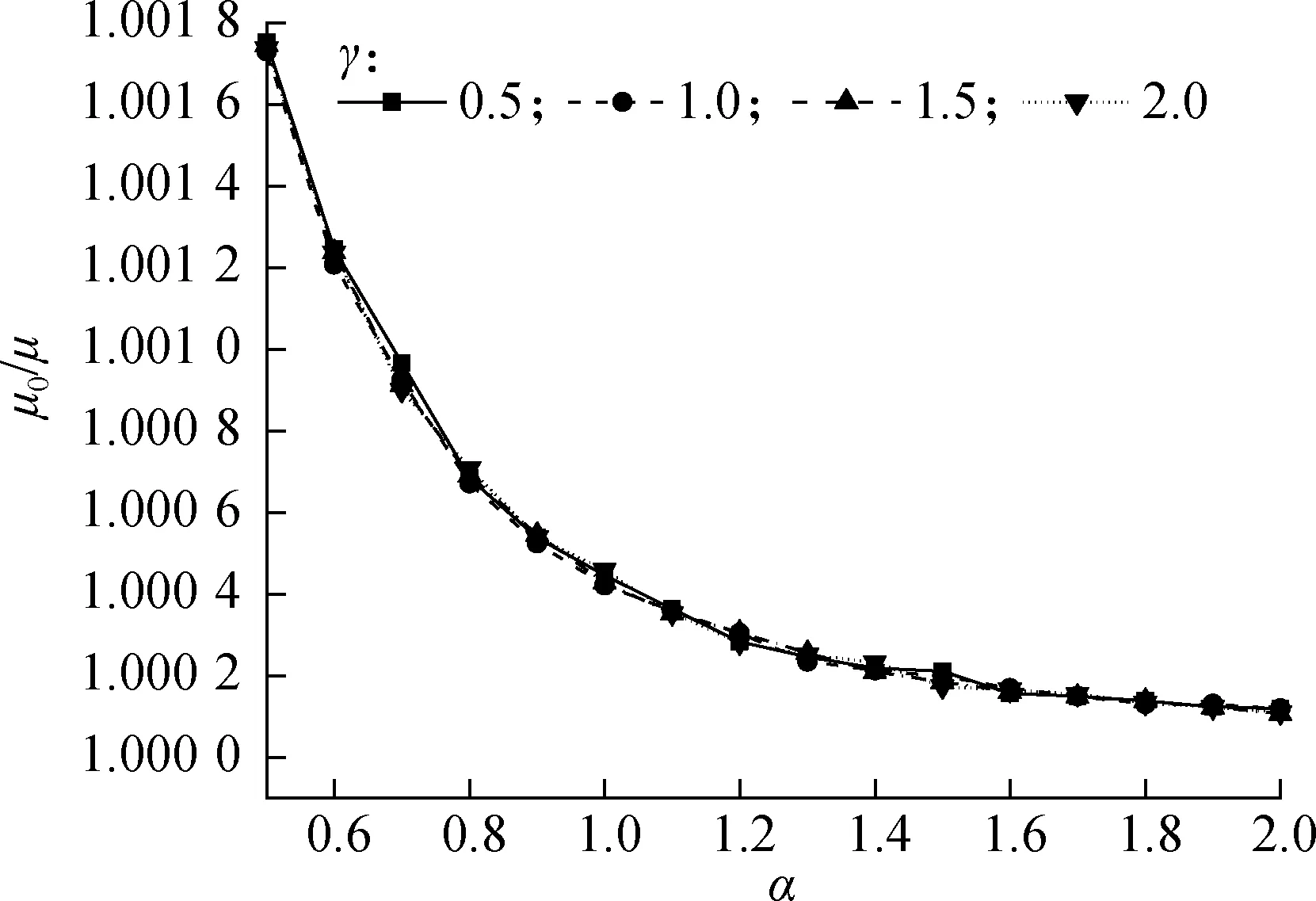
图3 不同活恒比下抗力更新前后均值比

图4 不同活恒比下抗力更新前后标准差比

4 评估分项系数计算

4.1 验证荷载选取

验证荷载效应模型的科学刻画是桥梁抗力分布更新研究的关键内容.合理做法是现场采集桥梁结构自投入运营时车流荷载下的作用效应，并建立科学、精准的数学模型进行研究分析.这无疑耗费大量的人力物力，而且我国不同区域车辆荷载分布差异较大，通过局部地区的车流荷载调查所得出的研究结果具有一定的局限性.

不同的活恒比表示不同结构类型的桥梁，而抗力的更新效果与恒载的具体取值无关.因此，下文依旧选取结构恒载标准值SG=100，活恒比重新选取，分别为0.1、0.25、0.5、1.0、1.5、2.5.考虑到验证荷载的差异性，选取验活比λ为0.8、1.0、1.5、2.0进一步进行研究分析.

4.2 不同基准期下目标抗力取值分析

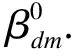
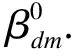
②取恒载效应标准值SG=100,活载效应标准值取为SQ, j=ρSG(ρ= 0.1，0.25，0.5，1.0，1.5，2.5)，验证荷载效应标准取值为SP, f=λSQ, j(λ=0.8，1.0，1.5，2.0).

③假定初始抗力为R0j=SG+SQ, j.

④根据表3计算对应安全等级d、不同运行状态l、不同基准期m下的抗力与荷载效应的分布参数SG(μSG,σSG)、SQ, ldjm(μSQ, ldjm,σSQ, ldjm)和R(μR, ldjm,σR, ldjm).

⑤采用验证荷载效应SP, f，依据式(6)对抗力的分布进行更新.

⑥根据一次二阶矩法(JC法)计算可靠度βldjmf.

4.3 不同基准期下评估分项系数计算分析

常用的分项系数确定方法有设计值法与优化方法，优化方法又分为抗力优化方法与可靠度优化方法[12].由于设计值法所需的永久作用、可变作用和结构抗力的敏感系数计算复杂，难以直接获取，本文采用优化方法进行计算分析.

抗力优化方法根据分项系数求出的抗力标准值与预先给定的目标可靠度求得的结构抗力标准值之差为最小的原则来确定分项系数的取值.基于以上思想，对于不同基准期而言，构件分项系数的选取应保证下式能达到最小值：

d=1,2,3;f=1,2,3,4

(9)

式中，Hdmf为所需抗力标准值与目标抗力值的绝对误差;Rldjmf为利用目标评估分项系数构建的抗力标准值.显然，一旦确定恒载分项系数γ′G，则可通过使式(9)的一阶偏导数等于0来确定对应的抗力分项系数γ′R,dmf，即

(10)

考虑到传统习惯，并保持与现行设计规范一致，令恒载评估分项系数γ′G=1.2.按照0.1的步长确定活载相应评估分项系数γ′Q在0.4～1.6范围内的13个值，根据式(10)可求解13个γ′R,dmf的取值.最优γ′R,dmf的选取需保证所需抗力标准值与目标抗力相对误差I值最小：

d=1,2,3;f=1,2,3,4

(11)

按照式(9)～(11)计算不同安全等级、不同评估基准期下的评估分项系数组合，得出的结果如表4所示.

表4 不同基准期下评估分项系数取值

当基准期取100 a时，分项系数的最优组合解中荷载分项系数γ′Q、γ′R的均值分别为1.08、1.25，与文献[10]中主要组合的计算结果1.1、1.298接近.为进一步验证计算流程的准确性，按照表4分项系数计算结果重新组合抗力标准值，结合相应变量的参数模型，采用JC法计算可靠度，结果如表5所示.

表5 不同基准期下可靠度

通过计算获取的可靠度与目标可靠度(见表1)接近.其中，最大幅度调整为0.05，不超过 0.1[10].这说明根据求解的分项组合系数计算目标抗力标准值能保证结构达到预定可靠水平，验证了分项系数计算过程的可行性.

4.4 不同验证期下评估分项系数取值

假定桥梁结构已服役年限分别为10、20、30、40 a.桥梁结构评估基准期取10 a，目标可靠度根据表1分别取3.37、3.14、2.87(分别对应一、二、三级).考虑到实际服役荷载与设计活载的差异性，取验活比λ=0.8，1.0，1.5，2.0，结合贝叶斯更新以及抗力优化法计算不同验证期下的评估分项系数，如表6所示.

表6 不同验活比下评估分项系数取值

通过对比表6、表4可知，当验活比λ=0.8，1.0 时，评估分项系数比(验证后分项系数与验证前的分项系数之比)均为1.0，这是因为较低的验证荷载水平对抗力分布的更新程度较小.当验活比λ=1.5时，随着验证期的增加，荷载评估分项系数比值逐渐减少.以二级安全等级为例，荷载评估分项系数比分别为0.94、0.81、0.69、0.69，抗力分项系数比分别为0.99、1.0、1.01、0.99；相应地，当验活比λ=2.0时荷载评估分项系数比为0.88、0.75、0.63、0.50，而抗力分项系数比分别为0.98、0.98、0.98、0.99.显然，抗力评估分项系数随着荷载评估分项系数的变化而波动，且均在1.0附近，为简化处理，建议取值为不考虑验证荷载的1.0倍.

为进一步检验表6的评估分项系数组合是否满足评估基准期内的目标可靠度，将分项系数按照上文的计算方法构建抗力，并在相应验证荷载期与验活比下对抗力进行更新，根据JC法求解可靠度，结果如表7所示.

表7 不同目标评估分项系数下的可靠度

通过对比表1和表7可知，同一安全等级，不同验活比与验证期下的计算可靠度与目标可靠度比较接近，最大差值为0.029，小于0.1，进一步验证了评估分项系数计算程序的合理性.

5 案例分析

选取某一典型钢筋混凝土简支T型梁桥，结合表6给定的评估安全系数进行安全性能评估，并与已有的规范建议系数取值(简称规范法)、设计值法进行对比分析.桥梁标准跨径为20 m，宽度为1 m(人行道)+7 m(行车道)+1 m(人行道)，设计荷载为《公路桥涵设计通用规范》(JTG D60—2004)公路Ⅱ级，T型梁及其横梁采用C40混凝土，钢筋采用HRB335钢筋，桥梁构造形式和主梁跨中截面尺寸如图5所示[13].

(a)横断面图

根据设计资料计算各梁的横向分布系数，得出1、2、3号梁的横向分布系数分别为0.51、0.46、0.40，因此选用1号梁进行研究分析.T型梁结构承载能力与恒载效应标准值分别为2 690、969.07 kN·m，荷载冲击系数为1.313.现行的汽车荷载效应标准值按照《公路桥涵设计通用规范》(JTG D60—2015)计算结果为1 023 kN·m.将衰减系数取为0.6～1.0来表示抗力不同衰减程度.采用设计值法计算基准期为10 a的分项系数，并与规范法以及本文方法建议系数(采用验证期为30 a的分项系数)根据式(2)对不同劣化程度下的桥梁安全指标进行计算分析，结果如图6所示.

由图6可知，当桥梁结构劣化系数处于0.82～1.0时，3种方法计算的结构安全评价指标均低于1.0，满足安全运营要求.当劣化系数处于0.73～0.82之间时，采用规范法进行安全指标评定的结果高于1.02，结构不满足安全水平，需进一步进行检测，而采用设计值法的计算结果依旧小于 1.0，结构可正常服役.与设计值法相比，规范法取值是根据基准期为设计基准期这一假定计算得出的.这一做法忽略了评估基准期对评估系数取值的影响，得出的评估结果与实际偏差较大.当劣化系数降低至0.72时，采用规范法与设计值法计算的安全指标分别为1.16、1.02，不满足运营安全指标，而采用本文提出的分项系数时评定结果分别为0.929、0.929、0.927、0.852、0.812，均小于1.设计值法虽然考虑了目标可靠度与基准期有关这一因素，但忽略了荷载效应在不同基准期下的取值不同，使得计算安全指标偏大.采用这一评定系数虽能保证结构的安全，但会造成不必要的浪费，不利于在役桥梁的运营成本控制.

图6 不同抗力劣化系数下的安全评价指标对比

当抗力劣化系数低于0.66时，采用验活比为0.8、1.0所对应的评估分项系数组进行评估时所得的结构安全指标分别为1.013、1.012，而采用验活比为1.5、2.0时计算的指标为0.929、0.886，结构依旧可以正常服役.这表明，随着验活比的增加，结构评定指标越低，结构安全储备越大.考虑验证荷载有助于更好地了解结构在运营荷载作用下的安全性能，进一步挖掘结构潜在承载能力.