浅埋单药包爆炸作用下饱和钙质砂基础液化数值模拟

吴拓展 宗周红 李明鸿 甘 露 伍 俊

(1东南大学土木工程学院, 南京 211189)(2中国人民解放军军事科学院国防工程研究院, 洛阳 471000)

钙质砂广泛分布于我国部分热带和亚热带地区海岸线,其主要成分为珊瑚碎屑,含部分珊瑚藻、贝壳及有孔虫碎屑,在爆炸冲击作用下,钙质砂基础可能会发生液化.液化问题以往主要集中于陆源砂地震液化的研究.以往发生的地震事例显示,砂土液化是造成各种建筑物破坏的主要原因之一[1].与地震作用类似,潜在的危化品爆炸事故、工程爆破作业和人为爆炸袭击事件等所引发的爆炸荷载作用下,饱和砂基础同样会发生喷砂冒水、变形沉降等严重的地基液化灾害.因此,开展爆炸荷载作用下饱和钙质砂基础的液化特性研究对保障工程结构安全具有重要意义.

相比于地震液化问题的广泛深入研究,对于爆炸强动载荷引起的饱和砂基础液化问题的研究还很缺乏,在工程设计中较少被考虑甚至直接忽略[2].现有砂土基础爆炸液化研究主要针对饱和陆源砂中的封闭爆炸情况[3].Ashford等[4]、Rollins[5]利用多点微差爆炸在饱和陆源砂土场地中制造人工振动液化环境,分析土中超孔隙水压力的发展规律,并研究液化场地中桩、地下管线的动力响应以及垂直排水系统的性能.Charlie等[6]进行了水下饱和砂土中爆炸液化试验,研究了初始相对密实度对孔隙水压力上升的影响.周健等[7]利用小型模型箱进行了小药量饱和砂土中的爆炸试验,通过测定爆炸液化后砂样排出水的体积改变评价饱和砂的密实效果.刘汉龙等[2]开展了一系列室外饱和陆源砂土中的单点及多点微差爆炸液化试验,分析了饱和砂土中单点和多点微差爆炸引起的土中孔隙水压力上升规律和爆炸液化的影响因素.

由于珊瑚砂特殊的海洋生物成因,珊瑚砂颗粒具有高棱角度、多孔隙、形状不规则等特点,呈现出低强度、高内摩擦角、易破碎等特性,使其在强度、变形和渗透性等力学性质上显著不同于一般陆源砂[8-12].因此,钙质砂基础的爆炸液化特性也将区别于一般陆源砂基础,有必要针对饱和钙质砂基础的爆炸液化问题开展深入研究.

现阶段针对饱和钙质砂基础液化特性的研究相对缺乏,主要集中在小当量封闭爆炸情况,饱和钙质砂基础爆炸液化的判别准则和分析方法仍不完善.徐学勇等[13-15]以南沙群岛美济礁钙质砂为主要研究对象,采用室内小型爆炸试验、理论分析和FLAC数值模拟等,总结出饱和钙质砂在爆炸作用下动力响应特性及爆炸应力波在钙质砂中传播和衰减规律.王亚松[16]开展了三相饱和钙质砂爆炸液化试验,结果表明三相饱和钙质砂的抗爆炸液化能力高于其他一般砂,主要原因为钙质砂颗粒易破碎,爆炸的能量被大大地损耗在破坏区,导致同样比例距离下,钙质砂的动力响应弱于其他一般砂.

目前,对于饱和砂土爆炸液化研究,主要集中在陆源砂现场试验方面.然而,现场试验对场地要求较高,数据监测范围有限,砂土种类试验范围有限,并且难以进行大量重复试验等,都在一定程度上制约了爆炸液化的研究.相比之下,数值手段可以在不引入外界环境干扰因素的情况下对土体结构内部进行研究,分析某些关键参数对结果的影响,且数值模拟成本远低于试验成本.因此本文基于非线性显式动力分析软件LS-DYNA和流固耦合算法,建立饱和钙质砂基础爆炸液化动力分析的精细化数值模型,然后利用已有的钙质砂室外爆炸液化试验结果验证数值模型的准确性和可靠性.在此基础上,分析浅埋单药包爆炸情况下比例距离、密实度、药包当量和混凝土桩等因素对饱和钙质砂基础土压力、孔隙水压力和液化特性的影响.

1 爆炸液化效应

饱和砂土的爆炸液化属于爆炸应力波传播的后效应问题[3].土中爆炸会产生一个持续时间仅在毫秒之内的应力波[17],在应力波传播过程中,孔隙水、气泡以及固体颗粒均会被压缩[18].对于饱和松散材料,如砂质土,由于孔隙流体和土壤骨架没有足够时间进行相对运动,孔隙水压力的增加阻止了爆炸压缩引起的体积减小.当孔隙水压力的增加达一定阈值,土体就会发生液化.通常采用超孔隙水压力比ru来衡量饱和土体动力液化发生程度：

(1)

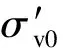
(2)

式中,R为目标点与爆心之间的距离;WTNT为TNT爆炸当量.

现有关于饱和砂土基础爆炸液化的分析和判别方法主要针对单药包封闭爆炸液化问题.饱和砂土中发生封闭爆炸时,自由面对爆炸波传播的影响几乎可以忽略,爆炸能量主要在土中传递衰减,可以最大程度地引起饱和砂土孔隙水压力的上升.在浅埋药包爆炸情况下,部分爆炸能量将溢出地表,通过土体自由面耗散,爆轰产物作用于上覆土体形成喷射物抛掷现象,从而使作用在土中导致孔隙水压力上升的爆炸能量相对减少[19].工程上通过定义比例埋深λ来衡量炸药的相对埋设深度：

(3)

式中,d为药包埋置深度.

由于土体性质的差异,饱和砂土中发生封闭爆炸的药包临界埋深一般比干砂或部分饱和砂土大[20].通常,饱和砂土中发生封闭爆炸的条件是药包的比例埋深大于2.5 m/kg1/3[21];对于部分饱和钙质砂,当药包的比例埋深大于等于2.25 m/kg1/3时,可以认为发生封闭爆炸[22].因此,为了确保在饱和钙质砂基础中发生的是浅埋爆炸,本文后续数值模拟计算中取炸药的比例埋深为2 m/kg1/3.

2 数值模型建立与验证

2.1 模型概述

采用非线性显式动力分析软件LS-DYNA建立了包括炸药和饱和钙质砂地基的三维精细化数值模型,如图1所示.数值模型为半径10 m、深度5 m的1/4圆柱,TNT爆炸当量为1 kg,埋置深度为2 m,比例埋深为2 m/kg1/3.整个模型均采用拉格朗日网格建立,网格最小尺寸为2 cm,最大尺寸为8.3 cm.模型对称面采用对称边界,模型四周采用无反射边界,以真实反映爆炸波在此的透射情况,实现用有限大的模型区域来模拟无限大的土体空间.模型底面设置为固定约束边界,模型上表面设置为自由边界以模拟基础与空气的接触面,从而真实反映爆炸波在此的透射情况.

图1 饱和钙质砂基础数值模型示意图(单位：m)

考虑到拉格朗日网格在爆炸近区会发生大变形和沙漏变形等畸变现象,在炸药包埋深处附近一定区域采用欧拉网格建立空气域,并通过*CONSTRAINED_LAGRANGE_IN_SOLID关键字与拉格朗日网格进行耦合,以模拟炸药的起爆过程并使爆炸波传播进入土体,炸药单元则通过关键字*INITIAL_VOLUME_FRACTION_GEOMETRY填充空气网格形成,通过修改关键字中的RADIUS参数直接改变球形炸药半径获得不同爆炸当量,软件自动划分药包网格.采用上述建模方式,可以使网格划分更为简单方便,并且可以避免因网格畸变导致计算无法收敛和结果失真的问题.

教师多年来面对的对象是相对自己综合素质低的受教育者打交道。长期的固定知识层次的交流，使教师的知识层次存在着很强的惯性，很难提高和充实。教师处在一个固定的教育教学圈子中，一直处在校园这个人际关系单纯的环境里，与社会外界交往的时空有限，能力也有限，教师到社会上办事往往机械死板，加之缺少有影响力的熟人，因而到处碰壁，从而形成诸如猜疑心理、嫉妒心理、自傲心理、自卑心理、强迫心理、孤僻心理等交际障碍。

2.2 材料模型

2.2.1 钙质砂土材料模型

饱和钙质砂采用*MAT_SOIL_AND_FOAM_FAILURE材料模型模拟,该模型适用于模拟砂等无黏性土,其在爆炸模拟中的适用性已得到了验证[23].在该模型中,加载和卸载遵循输入曲线,当压力达到设定的破坏压力时,单元将无法继续承载拉力.该模型采用10组数据对压缩状态方程进行多段线性逼近,其压力-体积应变关系曲线如图2所示[24],其中体积应变以相对体积自然对数表示.图中,V0为初始体积,V为变形后体积.

图2 土体压力-体积应变关系[15]

本文数值模拟中钙质砂模型的相关材料参数根据文献[24]确定,表1～表4分别给出了相对密实度Dr为30%、60%和90%的钙质砂材料模型参数.其中,ρs为钙质砂材料密度,G为钙质砂材料的剪切模量,卸载体积模量Ku=-dP/(dV/V0),dP为压力变化,dV为体积变化;a0、a1、a2为剪切屈服面系数;P为与体积应变相对应的压力;材料压实后卸载时可认为弹性卸载.

表1 不同相对密实度钙质砂材料物理参数

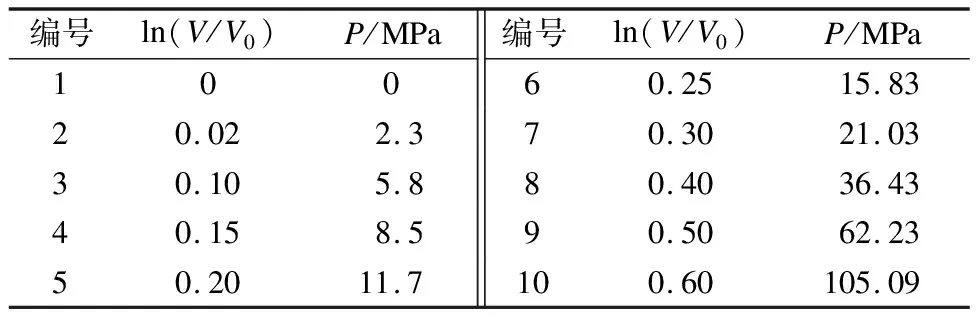
表2 相对密实度为30%的钙质砂材料模型参数

表3 相对密实度为60%的钙质砂材料模型参数

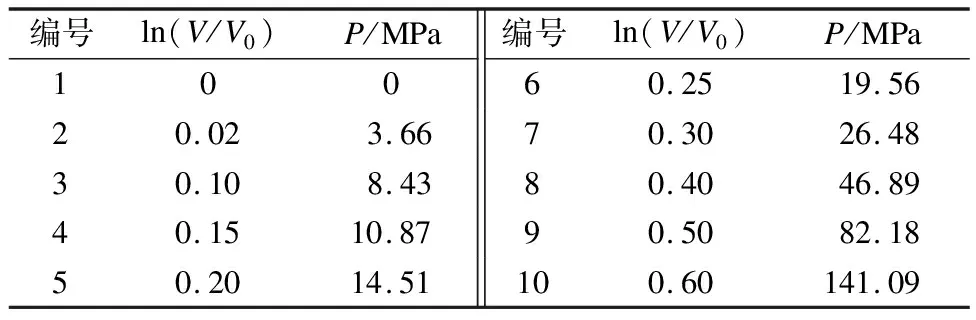
表4 相对密实度为90%的钙质砂材料模型参数

饱和砂土中的孔隙水通过关键字*CONTROL_PORE_FLUID和*BOUNDARY_PORE_FLUID添加到砂土材料模型中.LS-DYNA利用Terzaghi[25]提出的有效应力原理来模拟孔隙压力,

假设孔隙流体和砂土骨架占有相同的体积,并共同承载荷载.因此,单元总应力是土体骨架中的有效应力与孔隙流体中的静水压力之和.由于爆炸荷载频率高,诱发的超孔隙水压力没有时间消散,可以认为爆炸阶段土体不排水.表5给出了本文数值模型中孔隙水的相关参数.

表5 孔隙水相关参数

2.2.2 空气材料模型

在数值模拟中,假设空气为理想气体,采用*MAT_NULL材料模型和线性多项式状态方程*EOS_LINEAR_POL YNOMIAL进行模拟.线性多项式状态方程[26]的表达式如下：

Pair=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ6)E

(4)

式中,Pair为空气压力；C0～C6为多项式方程系数;μ=ρ/ρ0-1,ρ和ρ0分别为空气的密度和初始密度;E为单位体积内能.理想气体符合γ律状态方程,取C0=C1=C2=C3=C6=0,C4=C5=γ-1,则式(4)可以表达为

(5)

表6 空气材料参数

2.2.3 TNT炸药材料模型

TNT炸药采用*MAT_HIGH_EXPLOSIVE_BURN材料模型模拟,材料模型确定的参数包括质量密度、爆轰速度和Chapman-Jouguet压力(PCJ)[26].采用*EOS_JWL(Jones-Wilkins-Lee)状态方程[26]描述爆轰产物的状态,其表达式为

(6)

式中,Pblast为爆轰压力;Eb为每单位体积炸药的初始内能;Vb为相对体积,即爆炸后产生物质的体积与炸药初始体积的比值;A1、B1、R1、R2、ω为炸药的特征常数.本文采用的TNT炸药材料参数和状态方程参数取自文献[27],具体参数如表7所示.

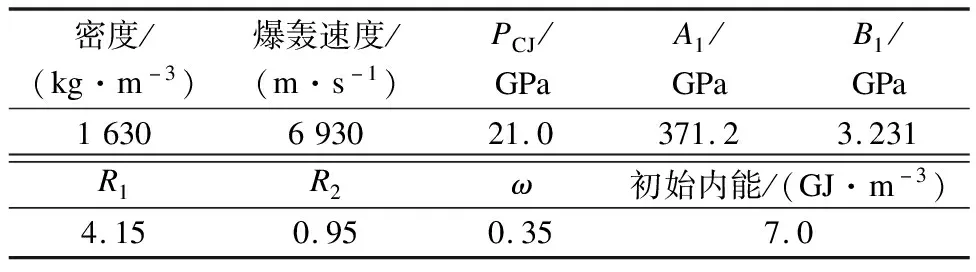
表7 炸药材料及状态方程参数[27]

2.2.4 混凝土桩材料模型

不考虑冲击波对混凝土桩的破坏情况,仅考虑加入混凝土桩后超孔隙水压的变化,因此混凝土材料使用MAT_ELASTIC材料模型进行模拟.混凝土材料密度为2 500 kg/m3,弹性模量为3.25×104MPa,泊松比为0.2.

2.3 数值模型验证

采用文献[16]开展的饱和钙质砂爆炸试验结果对数值模型进行验证,试验示意图及相应的数值模型如图3和图4所示.试验中,在直径2.0 m、高2.0 m的不锈钢圆柱形装置中对钙质砂进行蓄水饱和,然后在1 m埋深处引爆装药质量为0.064 kg的TNT球形药包,B1～B7为相应的传感器埋置点.利用本文提出的建模方法对试验过程进行数值模拟,将计算得到的饱和钙质砂土中不同比例距离处的超压值与试验结果相比较,如图5所示.从图中可见,数值模拟结果与试验所得经验公式基本一致,当比例距离小于1.0 m/kg1/3时,数值模拟结果大于经验公式结果,最大误差为18%;当比例距离大于1.0 m/kg1/3时,数值模拟结果基本在经验公式结果的±10%误差范围内.引起误差的主要原因为数值模型中采用了近似的饱和砂材料参数,室外试验中饱和砂的相对密实度为82.6%,而数值模拟采用了文献[24]中给出的相对密实度90%的饱和砂材料参数作为近似.总体来看,数值模拟结果与经验公式计算结果吻合较好,相对误差在合理的可接受范围内,可以认为采用上述方法建立的数值模型能够较好地预测爆炸冲击波在饱和钙质砂中的传播和自由场峰值压力,可以对饱和钙质砂基础进行孔隙水压力和爆炸动力液化分析.

图3 试验及传感器布置示意图[17](单位：cm)

图4 数值模型示意图

图5 数值模拟和经验公式计算的土压力峰值结果比较

3 数值结果分析

3.1 饱和钙质砂土压力分析

以60%相对密实度的饱和钙质砂为例,对饱和钙质砂基础中浅埋单药包爆炸冲击波传播引起的土压力进行分析.图6给出了比例埋深2 m/kg1/3的1 kg TNT装药爆炸下,水平比例距离为3、4和5 m/kg1/3处的土压力时程曲线.从图中可以看到：随着爆炸冲击波的到达,土压力值急剧增加,随后迅速衰减,压力值上下波动直到达恒定值.对于3种不同的比例距离,爆炸产生的土压力峰值随着比例距离的增大而减小,土压力峰值在0.05～0.10 MPa之间.表8给出了几种饱和陆源砂在爆炸荷载作用下的峰值土压力upk的经验计算公式,据此分别计算不同砂土在水平比例距离3、4和5 m/kg1/3处的峰值土压力如表9所示,并相应给出了钙质砂峰值土压力的数值模拟计算结果.由表9可知：在相同比例距离下,饱和钙质砂的土压力峰值小于普通陆源砂,其可能的原因是钙质砂颗粒易破碎,使得部分爆炸能量在爆炸近区被损耗.

图6 不同比例距离下饱和钙质砂土压力时程

表8 饱和陆源砂土中峰值压力经验公式

表9 不同比例距离下饱和砂土峰值压力 MPa

3.2 孔隙水压力分析

以60%相对密实度的饱和钙质砂为例,对浅埋单药包爆炸冲击波作用下的饱和钙质砂基础中的孔隙水压力进行分析.图7显示了爆炸过程中不同时间饱和钙质砂基础中的孔隙水压力分布,图8为水平比例距离分别为2、3和4 m/kg1/3处的超孔隙水压力时程曲线.由图7和图8可知：饱和钙质砂土受到冲击波作用后,将产生一个孔隙水压力峰值,形成类似于冲击波径向传播模式的孔隙水压力分布.爆炸冲击波到达时,土中孔隙水压力值在瞬间上升至一个远高于后期孔隙水压力累积的峰值,该孔隙水压力峰值主要是由冲击压缩波引起的;孔隙水压力达到峰值后将会迅速回落,经过一段时间累积后(约400 ms),孔隙水压力达到稳定值.从图8可以看到,比例距离2、3和4 m/kg1/3处的超孔隙水压力峰值分别为110.3、57.4和29.2 kPa;达到稳定的超孔隙水压力分别为17.5、11.7和5.0 kPa,孔隙水压力峰值和孔隙水压力稳定值均随比例距离的增加而明显减小.

(a)0 ms

图8 不同水平比例距离下饱和钙质砂超孔隙水压力时程图

图9为饱和钙质砂基础不同深度平面内达到稳定的超孔隙水压力比随比例距离的变化曲线.从图中可见,在相同水平比例距离下,深度越深,超孔隙水压力比越小,即药包下方土体距离药包越远,液化的可能性越小.

图9 不同深度同一水平面饱和钙质砂超孔隙水压力比与比例距离的关系曲线

王维国[20]、Studer等[30]、Charlie等[31]和Kummeneji等[32]曾分别基于饱和陆源松砂场地在封闭单药包爆炸下的液化试验结果,建立了超孔隙水压力比与比例距离的经验预测模型,用于对特定或者类似环境下砂土基础的爆炸液化情况进行预测,其具体形式及相应的场地性质如表10所示.

表10 单药包封闭爆炸下饱和陆源松砂液化的经验预测公式

仅考虑比例距离的影响,对数值模拟计算的超孔隙水压力比数据进行拟合,得到拟合公式如下：

ru=2.14-1.335lnZ

(7)

根据所得对数式拟合公式,在比例距离Z≤4.6 m/kg1/3的场地范围内,超孔隙水压力具有显著的累积(ru≥0.1);而Z≤2.35 m/kg1/3时将发生完全液化.与表10所列不同陆源松砂场地爆炸液化影响范围相对比,饱和钙质砂完全液化域与普通陆源松砂基本一致,孔隙水压力的影响域远小于普通陆源松砂.由前述分析可知,饱和钙质砂颗粒易破碎使得爆炸能量在爆炸近区被大量消耗,因此在相同比例距离下,饱和钙质砂峰值土压力小于普通陆源松砂,由土中压缩波引起的超孔隙水压力也小于普通陆源松砂.因此,可以认定饱和钙质砂基础相对于普通陆源松砂基础更不易发生液化.

3.3 不同爆炸当量对孔隙水压力的影响

为研究爆炸当量对饱和钙质砂基础爆炸液化特性的影响,保持比例埋深2 m/kg1/3不变,对4种(1、8、64、125 kg)不同爆炸当量条件下60%相对密实度饱和钙质砂基础的爆炸液化响应进行分析.图10给出了不同爆炸当量爆炸条件下药包埋深平面内比例距离2 m/kg1/3处的孔隙水压力时程曲线.由图可知,同一比例距离下,爆炸当量越小,孔隙水压力达到稳定值所需时间越短,稳定孔隙水压力值越小.图11给出了在同一比例埋深下不同爆炸当量埋深平面内的超孔隙水压力比与比例距离的关系曲线.结合图10与图11可得：在同一2 m/kg1/3比例埋深下,相同比例距离处,稳定孔隙水压力值随爆炸当量的增加而增大;在水平比例距离Z≤3 m/kg1/3范围内,超孔隙水压力比随着爆炸当量的增加而减小.这是因为当比例埋深相同时,爆炸当量越大,药包埋深越大,该处饱和钙质砂的初始竖向有效应力也越大,因而在比例距离相同的一定范围内超孔隙水压力比变小.这与Kummeneje等[32]通过封闭单药包饱和钙质砂土爆炸液化试验得出的结论相似.

图10 比例距离2 m/kg1/3不同爆炸当量下的饱和钙质砂孔隙水压力时程图

图11 比例埋深2 m/kg1/3下不同爆炸当量埋深平面内的超孔隙水压力比与比例距离的关系曲线

3.4 不同相对密实度对孔隙水压力的影响

图12给出不同相对密实度条件下,药包埋置深度(2 m)平面内超孔隙水压力比与比例距离的关系.从图中可见,在相同比例距离条件下,超孔隙水压力随相对密实度的增大而减小.30%相对密实度的饱和钙质砂完全液化范围域(ru=1.0)和超孔隙水压力显著累积范围域(ru≥0.1)与60%相对密实度饱和钙质砂基本一致;在超孔隙水压力具有显著累积范围域内,30%相对密实度的饱和钙质砂超孔隙水压力比随比例距离下降的速度更加缓慢.90%相对密实度的饱和钙质砂的完全液化范围和超孔隙水压力显著累积范围均远小于60%和30%相对密实度的饱和钙质砂.以比例距离3 m/kg1/3为例,与30%相对密实度的饱和钙质砂相比,60%相对密实度饱和钙质砂的超孔隙水压力比减少了18.5%,而90%相对密实度饱和钙质砂的超孔隙水压力比则减少66.2%.上述结果表明：提高饱和钙质砂的相对密实度可有效防止饱和钙质砂基础发生液化.

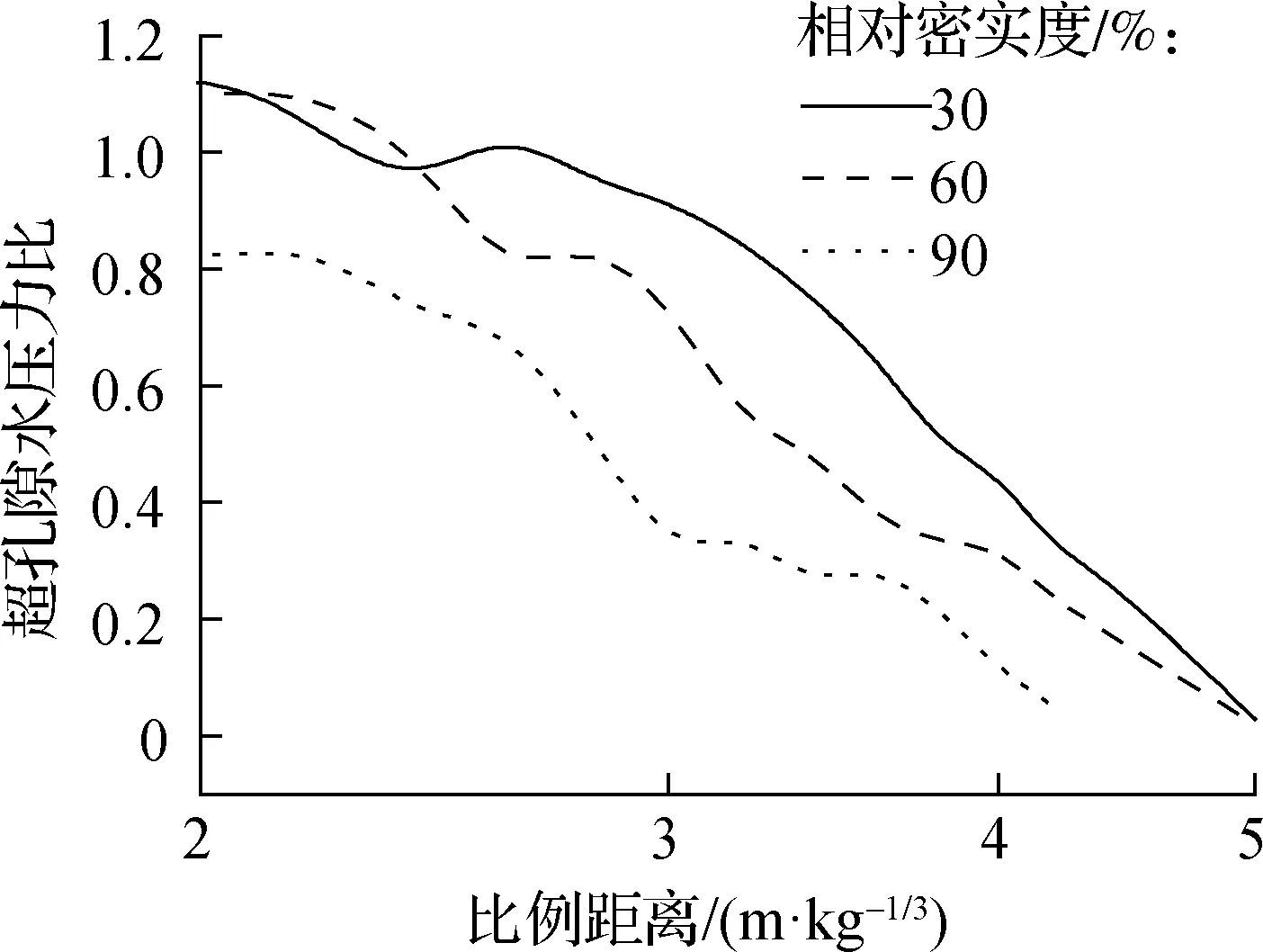
图12 不同相对密实度饱和钙质砂在同一水平面内的超孔隙水压力比与比例距离的关系曲线

3.5 混凝土桩对孔隙水压力的影响

根据所得对数式拟合公式(7),饱和钙质砂完全液化域为爆炸中心半径2.35 m范围,超孔隙水压显著累积域为爆炸中心半径4.60 m范围.分别在饱和钙质砂完全液化域和超孔隙水压显著累积域的域内和域外设置混凝土桩,以3.2节中比例埋深2 m/kg1/3的1 kg TNT药包在60%相对密实度饱和钙质砂基础中爆炸工况为对照组(工况1),研究混凝土桩距药包水平距离对饱和钙质砂基础中超孔隙水压力的影响,分析工况如表11所示.混凝土桩加固饱和钙质砂基础的数值模型如图13所示.

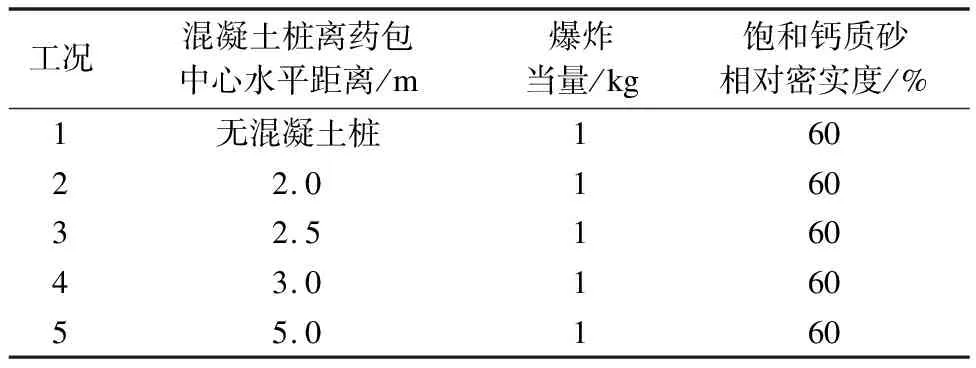
表11 混凝土桩加固基础计算工况

图13 混凝土桩加固饱和钙质砂基础有限元模型(单位：m)

图14给出了距药包中心2 m水平距离处布置混凝土桩(工况2)条件下,不同比例距离处孔隙水压力时程曲线,可见孔隙水压力在70 ms左右达到稳定值.无混凝土桩加固时,饱和钙质砂基础孔隙水压力在400 ms才达到稳定值(见图8),采用混凝土桩加固后饱和钙质砂基础孔隙水压力达到稳定所需时间节省了330 ms.

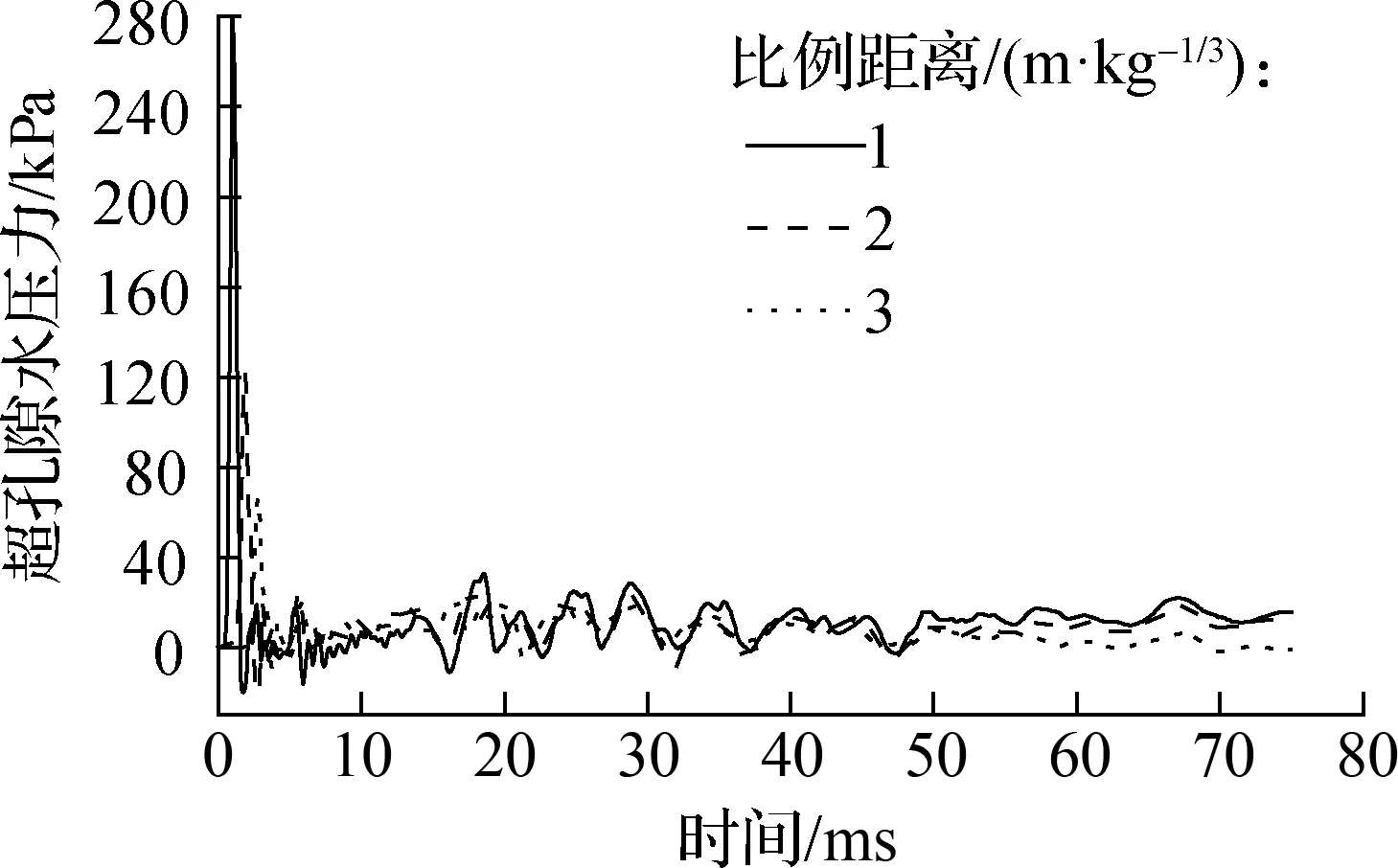
图14 不同比例距离处饱和钙质砂孔隙水压力时程图(工况2)

图15给出了不同混凝土桩加固工况下,饱和钙质砂基础超孔隙水压力比随比例距离的变化曲线.从图中可以看到,与无混凝土桩加固的饱和钙质砂基础(工况1)相比,在其完全液化域范围内加入混凝土桩(工况2)可以有效抑制超孔隙水压的发展,加固后基础在爆炸近区超孔隙水压比小于0.8,整个基础未发生完全液化的现象,超孔隙水压力具有显著累积域的范围缩小为3.90 m,相比未经混凝土桩加固的基础减小约15.2%.在无混凝土桩加固基础(工况1)完全液化域范围外设置混凝土桩(工况3、工况4和工况5),也能有效地减小基础的液化范围,并降低未加固基础液化范围内的孔隙水压力比.此外,混凝土桩布置距离药包水平距离越近,对降低孔隙水压力比的作用越明显.

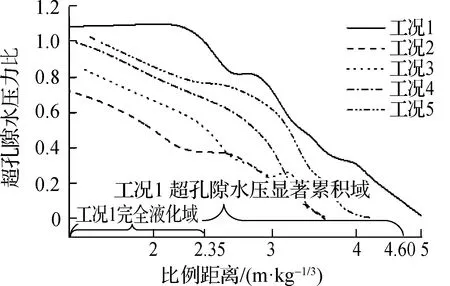
图15 不同混凝土桩加固条件下基础超孔隙水压力比与比例距离的关系曲线

对比图15和图12可见,图12中90%相对密实度饱和钙质砂域的超孔隙水压力比和超孔隙水压显著累积域大于图15中设置混凝土桩的饱和钙质砂域.由此可知，在爆炸近区设置混凝土桩加固较增大相对密实度对降低基础液化范围内孔隙水压力比的作用更显著,是抑制饱和钙质砂基础发生液化较为有效的方式.

4 结论

1)饱和钙质砂土受爆炸冲击波作用后将产生一个远高于后期孔隙水压力累积的超孔隙水压力峰值,超孔隙水压力经一段时间累积后将达一个稳定值.超孔隙水压力峰值和稳定孔隙水压力均随比例距离增加而明显减小.在相同水平比例距离下,药包下方土体距离药包越远,发生液化可能性越小.

2)基于普通陆源松砂封闭爆炸液化经验预测公式,修正得适用于浅埋单药包作用下饱和钙质砂基础爆炸液化分析的经验公式.对于饱和钙质砂基础,在比例距离Z≤4.60 m/kg1/3场地范围内,超孔隙水压力具有显著累积(ru≥0.1);当Z≤2.35 m/kg1/3时,将发生完全液化.饱和钙质砂基础完全液化域和普通陆源松砂基础基本一致,孔隙水压力影响域则远小于普通陆源松砂.在相同比例距离下,饱和钙质砂相对于普通陆源松砂更不易发生液化.

3)当比例埋深一定时,爆炸当量越小,孔隙水压达到稳定值所需时间越短,稳定孔隙水压力值越小;比例埋深一定时,在一定水平比例距离内,超孔隙水压力比随着爆炸当量的增加而减小.

4)在相同比例距离处,超孔隙水压力随着相对密实度的增大而减小,增大土体的密实度可以有效防止饱和钙质砂基础发生液化.

5)使用混凝土桩对饱和钙质砂基础进行加固,可以有效遏制砂土基础发生液化.在未加固基础的完全液化域中加入混凝土桩,可以使基础爆炸近区的超孔隙水压力比小于0.8,从而使整个基础不发生完全液化.将混凝土桩布置在完全液化域范围外,可以有效地减小基础液化范围,降低液化范围内的孔隙水压力比.混凝土桩布置距离爆心越近,对地基液化的遏制能力越强.相比于增加整个饱和钙质砂域的相对密实度,在爆炸近区使用混凝土桩加固更能有效地减小超孔隙水压力比,是抑制饱和钙质砂基础发生液化更为有效的方式.