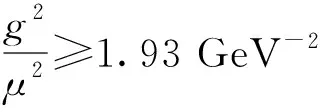袋模型下奇异星的非牛顿引力效应

皮 春 梅

(1.湖北第二师范学院物理与机电工程学院， 武汉 430205；2.湖北第二师范学院天文学研究中心， 武汉 430205)

物态方程是理论研究致密星结构和性质的重要输入量，它给出了物质内部压强P和密度E之间的关系.结合广义相对论下的流体静力学平衡方程(即TOV方程)和物态方程，可以计算致密星的密度、不同半径处的压强以及质量和半径等物理性质.不同的物态方程会给出不同的致密星内部成分和结构.20世纪60年代Gell-Mann M和Zweig G建立了强子结构的夸克模型，中子星内部物质组分有了更多的可能性.1984年，Witten E提出了奇异夸克物质设想[1]：由数量近乎相等的u、d、s夸克组成的夸克物质比56Fe更稳定.根据这个设想，致密星可能是由u、d、s三味夸克物质所组成的奇异星[2].

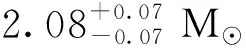
但是，在对引力的认识还并不完善的今天，对此还不能完全肯定.在统一引力和其他三种基本相互作用力，即电磁相互作用，强相互作用和弱相互作用的过程中，人们发现描述引力的平方反比关系不再成立.平方反比关系需要根据弦理论预测的其他时空维度的几何效应(或者粒子物理标准模型之外的超对称理论所预言的弱耦合玻色子的交换)做出修正[5-6].尽管至今尚未确认非牛顿引力的存在，已经有很多地面实验和天文观测对偏离牛顿引力程度的上限给出了限制，相关文献综述见[7].

中子星和奇异星的非牛顿引力效应已经得到广泛研究[8-16]，发现在致密天体中这种非牛顿引力可能会具有明显的物理效应，为软物态方程支持大质量致密星(中子星和奇异星)带来了希望.

1 奇异夸克物质的物态方程

夸克物质的状态方程本质上应该由量子色动力学(QCD)来计算，鉴于对低能强相互作用非微扰特性认识的不足，这一计算方法还不能进行.在实际计算中经常采用唯象模型，例如袋模型.此模型忽略夸克间的动力学相互作用，视其为理想气体.各类粒子的巨热力学势分别为[17-18]：

(1)

(2)

(3)

其中,mi和μi分别为粒子的质量和化学势.

通过热力学关系可以利用巨热力学势计算系统的各热力学量，如各种粒子数密度、压强和能量密度等.第i(i=u，d，s，e)种粒子的数密度是

(4)

夸克物质通过弱相互作用保持化学平衡.各类粒子化学势μi之间满足平衡条件

μd=μs=μu+μe.

(5)

作为一个稳定系统，还应当满足电中性条件要求：

(6)

重子数密度为

(7)

不考虑非牛顿引力效应时，能量密度为

(8)

相应地，压强为

(9)

这里B是袋常数.

本文忽略u夸克和d夸克的质量，s夸克的流质量取ms=93 MeV[19]，选取具有代表性的袋常数B1/4=140 MeV.

2 非牛顿引力效应

根据Fujii理论[20]，非牛顿引力可以表述为在传统的引力势基础上增加一个汤川型的修正项，即

VN(r)+VY(r)，

(10)

其中,G∞=6.6710×10-11N·m2/kg2，α是无量纲的汤川引力强度参数，λ是短程相互作用的特征长度.利用矢量玻色子交换模型，

其中，±分别代表标量(+)和矢量(-)玻色子，μ，g和mb分别是玻色子-重子耦合常数，玻色子质量和重子质量.

非牛顿引力效应可近似地通过物态方程来描述，而保持爱因斯坦场方程不变.汤川型的修正项对能量密度的贡献为

(11)

(12)

通过积分很容易得到，

(13)

因为原则上研究对象很大，可以取R→∞，故

(14)

综上，考虑非牛顿引力效应，奇异夸克物质的能量密度为

E=EQ+EY，

(15)

其中EQ由(8)式给出.

相应地，汤川型修正项对压强的贡献为

(16)

假定玻色子质量与介质密度无关[9]，有

(17)

考虑非牛顿引力效应，奇异夸克物质的压强为

P=PQ+PY，

(18)

其中,PQ由(9)式给出.

这里需要指出，非牛顿引力理论是超越了广义相对论的理论.众所周知，平方反比关系是广义相对论在弱场低速情形下的近似.非牛顿引力理论(具体到本文，是在传统的引力势基础上增加一个汤川型的修正项)下，平方反比关系不成立.实际上，超越相对论的其他一些引力理论，如f(R)理论，在弱场低速情形下也不满足平方反比关系[6].

如Shao所述[23]，广义相对论的场方程中有两个部分，其一是时空几何，其二是物质与能量.在对广义相对论做修正时，既可以修正时空几何部分，也可以修正物质与能量部分，两种途径是简并的.在研究非牛顿引力对奇异星质量—半径关系(图3)的影响时采用公式(15)和(18)所给出状态方程，这实际上是修正了广义相对论的物质与能量部分，而广义相对论的时空几何部分保持不变.于是，仍然可以采用原来的广义相对论所推导出的TOV方程.

3 数值计算结果与讨论

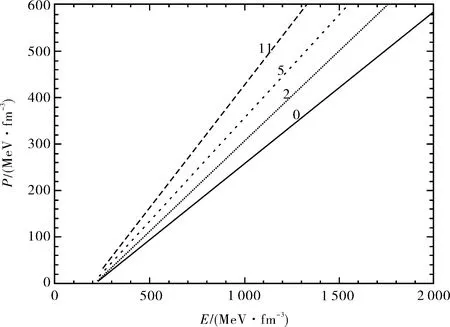
注：曲线旁边的数值代表非牛顿引力参数的取值，单位是GeV-2.图1 考虑非牛顿引力后MIT物态方程的密度-压强关系Fig.1 Relation between pressure and energy density in MIT model of quark matter with the non-Newtonian gravity

图2给出了不同参数下汤川型非牛顿引力效应的修正项对能量密度的贡献随重子数密度的变化.随着重子数密度的增大，修正项能量密度越大.其实从方程(14)中就可以看出修正项能量密度随着重子数密度的平方单调增加的.

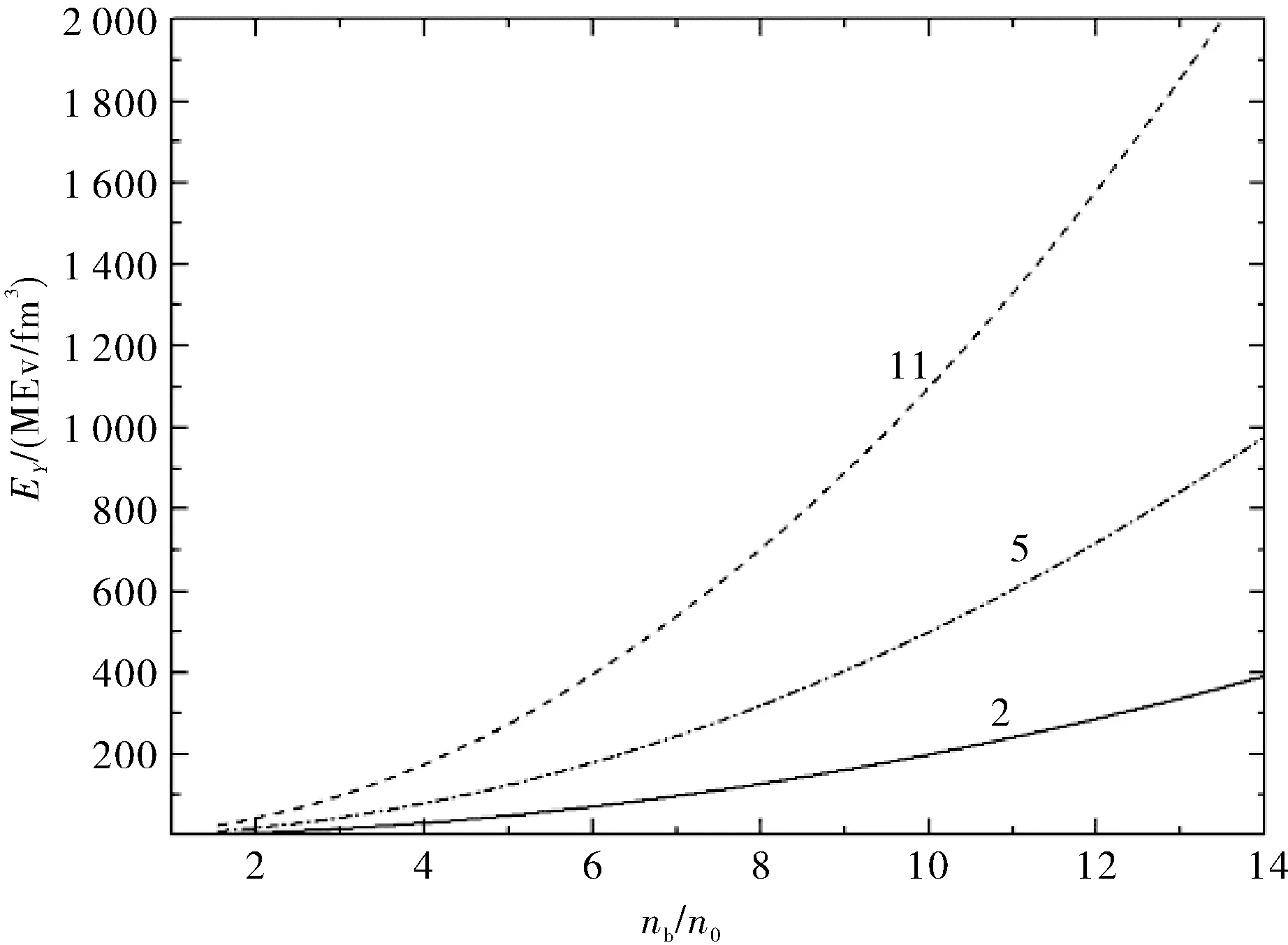
注：n0=0.17 fm-3是标准核饱和密度.图2 汤川型非牛顿引力效应的修正项对能量密度的贡献随重子数密度的变化Fig.2 The extra density due to the non-Newtonian component as the function of

注：红色实线对应于 此时理论给出的奇异星最大质量是2.08M⊙.绿色实线给出了目前观测中发现的最大质量脉冲星(PSR J0470+6620)的数据，它的质量是2.08M⊙.图3 引入和没有引入非牛顿引力效应的情况下奇异星的质量—半径关系Fig.3 The mass-radius relation of strange stars with several typical sets of model parameters

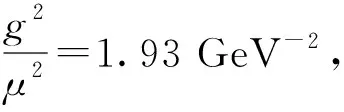
图4 观测到的脉冲星最大质量(2.08M⊙)对非牛顿引力参数空间的限制Fig.4 Upper bounds on the strength parameter |α| respectively,the boson-nucleon coupling constant g as a function of the range of the Yukawa force μ and the mass if hypothetical bosons,set by differrent experiments

4 总结