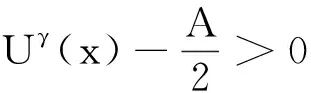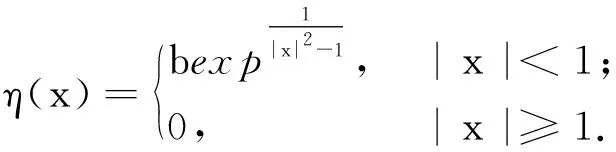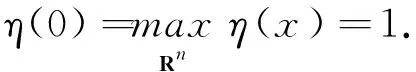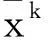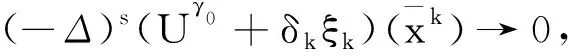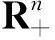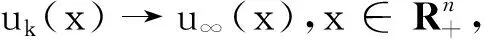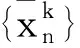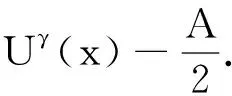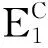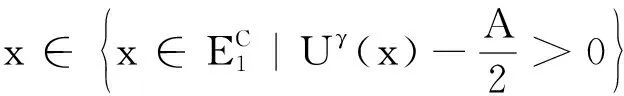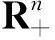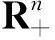带Hardy位势分数阶Laplace方程解的单调性

管 睿， 沃维丰

(宁波大学数学与统计学院， 浙江 宁波 315211)

本文研究半空间上带Hardy位势分数阶Laplace方程的De Giorgi型边值问题的单调性.即

(1)

及

|u(x)|≤1，

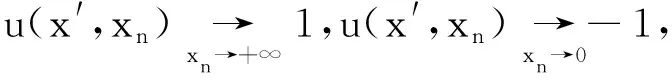
x=(x1，x2，…，xn)=(x′，xn).(-Δ)s是非局部算子，定义为：

(2)

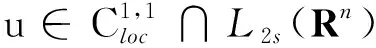
分数阶Laplace方程解的性质问题已经被诸多国内外学者研究，其中一类带Hardy位势的分数阶Laplace方程逐渐成为研究的热点[1-3].其研究方法包括积分方程方法[4]、移动平面法[5]、sliding方法[6-7]等[8-10].本文主要采用sliding方法得到了方程(1)在半空间上的解关于xn是单调递增的，且只依赖于xn.笔者研究的是带Hardy位势的分数阶Laplace方程，由于分母在x=0处会产生奇性，故研究上半空间中方程解的单调性.根据目前已知文献，还未有人运用sliding方法对该方程进行研究，本文的结果有望推导至更一般的情况．

文献[6]中陈文雄和武乐云运用了sliding方法研究了方程

(-Δ)su(x)=f(u(x))．

分别得到了该方程在有界区域和无界区域中，解关于xn的单调性，并证明了狭窄区域原理和无界区域极值原理．

文献[1]中Hu运用了移动平面法研究了带Hardy位势的分数阶Laplace方程

其中，02s.分别证明了该方程的解在有界区域和无界柱体中的对称性和单调性．

本文主要研究结论如下.

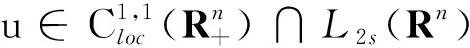
的解，并且

|u(x)|≤1，

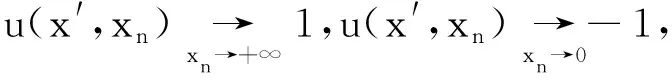
(3)

f(x，t)和g(t)满足:

(H1)f(x，t)和g(t)关于t局部Lipschitz连续，且g(t)≤0；

(H3) 存在δ>0使得f(x，t)和g(t)在[-1，-1+δ]和[1-δ，1]上关于t非增,则u关于xn严格单调递增，且只依赖于xn．

1 预备知识

本文需要用到的引理如下.

引理1[6]令D是Rn中的开集(可能无界、不连通)，设

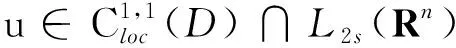
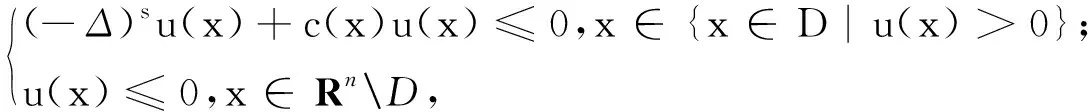
以及c(x)≥0.则有

u(x)≤0，x∈D．

这里，Cn，s为(2)中的常数，C0满足

2 定理1的证明

定义1取γ>0，设

uγ(x)=u(x′，xn+γ)，

定理1的证明分为三步完成．

第一步：将证明对充分大的γ有

(4)

若上述结论不成立，则有

(5)

u(x′，xn)≥1-δ，xn≥b，

及

u(x′，xn)≤-1+δ，0

并且存在常数M>b使得

(6)

其次，若取γ≥b-a，x在上半空间中，则x和x+(0，γ)中至少有一个在集合{y|yn≥b}或集合{y|0

uγ(x′，xn)≥1-δ，xn≥b，

或者

u(x′，xn)≤-1+δ，0

又由于f(x，t)和g(t)在[-1，-1+δ]及[1-δ，1]上关于t非增，因此，

f(xγ，uγ(x)) ≤0

(7)

由(6)和引理1可得

这与(5)矛盾，则得到(4)，即对充分大的γ有

从而可得

(8)

第二步：(8)给滑动平面提供了一个起始位置，从γ=b-a开始减小γ.同时证明对任意0<γ

(9)

设γ0为γ的下确界，即

下面证明γ0=0.若结论不成立，则γ0>0.将证明γ0在满足(9)的情况下仍可继续减小一点点．

1) 首先证明

(10)

若(10)不成立，则有

那么可以找到一个序列

{xk}⊂Rn-1×[a，b]，k=1，2，…，

满足

Uγ0(xk)→0，当k→∞时.

(11)

设函数η(x)为：

设

ξk(x)=η(x-xk)．

从而存在一个序列{δk}→0使得

Uγ0(xk)+δkξk(xk)>0．

Uγ0(xk)+δkξk(xk)>Uγ0(x)+δkξk(x)，

又由

结合(11)有

(12)

因为f(x，t)和g(t)都是连续函数，所以有

Cδk→0，当k→∞时.

(13)

另外，有

0.

(14)

由(13)和(14)可得

(15)

在引理2中取u=Uγ0+δkξk可得

由(12)、(15)及δk→0，可得

(16)

设

又由(16)可得

从而有

(17)

则有

u∞(x′，xn)=u∞(x′，xn+γ0)=

u∞(x′，xn+2γ0)=…=u∞(x′，xn+kγ0)，

∀k∈N.

(18)

(19)

2) 接下来证明存在ε>0使得

(20)

由(19)可知存在小的ε>0满足

(21)

因此,只需证明

(22)

若(22)不成立，则有

(23)

根据(23)不妨设存在M>b，使得

∀γ∈(γ0-ε，γ0].

(24)

设

E1=(Rn-1×(0，a))∪(Rn-1×(b，M))，

则有

(25)

(26)

当x∈Rn-1×(0，a)时，有uγ(x)≤u(x)≤-1+δ，同理可得结论(26)．

(27)

由(25)和(27)及引理1可得

这与(23)矛盾.所以(22)成立.从而可证得(20)，而这与γ0的定义相矛盾.因此有

第三步：这一步将证明u关于xn是严格单调递增的，且只依赖于xn．

由前两步可知

f(x0，u(x0))-f((x0)γ，uγ(x0))≤

f((x0)γ，uγ(x0))=0.

(28)

(-Δ)s(Uγ(x0))=

(29)

因此，(28)与(29)矛盾.则有

即

u(x)

这说明u关于xn是严格单调递增的．

最后，证明u只依赖于xn．

实际上，设

μ=(μ1，μ2，…，μn)，μn>0．

由整个证明过程可知，当uγ(x)=u(x+γμ)时，结论同样成立.对所有μ，参考第一、二步的证明，可得

当μn→0时，u是连续的，因此对所有μ，μn=0，有

u(x)≤u(x+γμ)．

从而对所有μ，μn=0，有

u(x)=u(x+γμ)，

这说明u不依赖于x′.则

u(x)=u(xn)，

即u只依赖于xn．

定理1的证明完成．