不适定线性二层规划问题的一种新的激励模型

贾世会， 王兴趣

(1.武汉科技大学理学院， 武汉 430081； 2.冶金工业过程系统科学湖北省重点实验室， 武汉 430081)

二层规划问题是一种具有递阶结构的系统优化问题，由上、下两层优化问题构成，上层和下层问题都有自己的目标函数和约束条件，上层问题的目标函数和约束条件不仅与上层决策变量相关，而且还依赖于下层问题的最优解，而下层问题的最优解又受上层决策的影响.不管是上层问题还是下层问题，目的都是达到各自最优，但又同时受到对方决策的影响.迄今为止，二层规划问题已经在交通规划、电力市场、生态环境、工程设计等[1-8]众多应用领域发挥着极其重要的作用.然而，作为一类NP-hard[9]问题，即使是一个线性二层规划问题[10-11]一般也是很难求解的.本文考虑以下的线性二层规划问题[12]：

s.t.A1x≤b1，

(1)

y∈ψ(x)，

其中，ψ(x)是下层问题反馈解的集合，

s.t.A2x+B2y≤b2，

(2)

这里，x，c1∈Rn，y，d1，d2∈Rm，A1∈Rp×n，b1∈RP，A2∈Rq×n，B2∈Rq×m，b2∈Rq．

设X={x∈Rn|A1x≤b1，x≥0}和Y(x)={y∈Rm|B2y≤b2-A2x，y≥0}.

若ψ(x)不唯一，即下层问题对于上层决策变量的每个(或某些)取值可能有多个对应方案.那么上层决策者很难预测下层决策者会在ψ(x)反馈哪一个方案给自己，从而使得上层决策者很难确定自己的最终决策.通常称此类问题为不适定性二层规划问题(简称为IBPP).

对于不适定性二层规划问题，这里存在两种极端情况，第一种情况假设下层决策者完全与上层决策者合作，即会反馈一个对上层决策者而言最优的解，此种情况称作乐观模型[4，13-14]，具体形式如下：

(3)

相反，第二种情况假设下层决策者完全不与上层决策者合作，即反馈一个最差的结果给上层，此时称作：悲观模型[15-19]，具体形式如下：

(4)

由于合作与竞争在现实生活中是共依共存的，乐观和悲观的解决方案可能都不是解决实际问题的最佳选择.1995年，对于Stackelberg问题中的乐观和悲观模型，Aboussoror和Loridan[20]首先提出了协调解的概念；随后，Mallozzi和Morgan[21]给出了上层决策者掌握了下层决策者部分信后的协调解构造；继而，引入合作指标λ来描述下层决策者的合作程度.2002年，Cao和Leung[22]提出了不适定线性二层规划问题的部分合作模型：

(5)

在这个模型里，λ是一个参数，它使得模型变得更加难以求解.

本文提出了问题(1)的一个协调模型，引入利润分配比例β，此时，β是一个变量，而不是参数.同时，根据约束条件，构造两个精确罚函数，将原模型进行等价转换.数值结果验证了该方法的可行性.最后，将此方法与文献[22]的部分合作模型进行比较，结果显示，虽然两种方法中下层决策者的收入是相同的，但本文方法得到的上层决策者的利润要优于Cao和Leung[22].

1 协调问题，激励模型

为了建立理论结果，首先给出如下主要假设.

假设：

(A1) 对于任意的x∈X，Y(x)≠∅，存在着一个紧子集W⊆Rm使得对所有的x∈X，Y(x)⊂W.

(A2) 集合X是一个有界多面体.

取β为上层决策者最终利润分配比例，基于激励的原则，上层决策者将自身利润(1-β)的份额给予下层决策者以激励下层决策者与自己合作，于是可得如下协调模型：

s.t.x∈X，

y∈ψ(x)，

(6)

0≤α≤β≤1，

(7)

(8)

由对偶性理论，问题(2)的对偶问题如下：

(9)

s.t.x∈X，

A2x+B2y≤b2，

(10)

0≤α≤β≤1，

y≥0，z≥0．

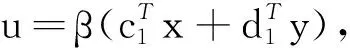
Z2={(x，y，u)|x∈X，A2x+B2y≤b2，

于是，问题(10)转化为：

(11)

(z，β)∈Z1，(x，y，u)∈Z2.

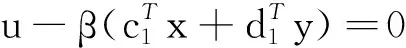
s.t.(z，β)∈Z1，

(12)

其中，k1，k2>0是惩罚参数.令

表示问题(12)的目标函数.

假设k1，k2>0是固定的，(z，β)∈Z1，令

(13)

则有如下结论．

定理1若满足假设(A1)和(A2)，则问题(12)在Z1×V(Z2)中至少有一个解，其中V(Z2)表示集合Z2的顶点集.

证明已知k1，k2>0，(z，β)∈Z1，函数θ(z，β)是凹的，那么，问题(13)有一个解(x，y，u)∈V(Z2).因为多面体Z2是有界的，所以问题(13)可以重写为：

其中，(xi，yi，ui)∈V(Z2)且|V(Z2)|表示集合Z2的顶点数.

对于每一个(xi，yi，ui)∈V(Z2)，设

即

由目标函数的凹性，得

(x*，y*，u*)表示问题(13)的解，相应的，(z*，β*，x*，y*，u*)∈Z1×V(Z2)是问题(12)的一个解.

2 算法和主要结果

根据第2部分的结果，给出问题(6)～(8)的算法.

算法：

Step 0.选择k1=k2>0，γ>1．

备注多面体的顶点数是有限的，其所有的顶点都可以用参考文献[23-24]中的方法列出.

对于(xi，yi，ui)∈V(Z2)，可以将问题(12)转化为一系列凹规划问题P(xi，yi，ui)，具体如下：

(zi，βi)表示上式的解，那么可以得到

下面的结果表明Step1-Step2-Step1和Step1-Step3-Step1将在有限次迭代之后终止.

为了简单起见，定义：

D2={(x，y，z，u，β)|(x，y，z，u，β)∈D1，

D3=

{(x，y，z，u，β)|(x，y，z，u，β)∈D1，π(x，y，z)=

D4={(x，y，z，u，β)|(x，y，z，u，β)∈D1，

D5={(x，y，z)|(x，y，z，u，β)∈D1，

π(x，y，z)>0}，

D6={(x，y，z，u，β)|(x，y，z，u，β)∈D1，

π(x，y，z)=0，

不失一般性，考虑如下三种情况.

于是有如下定理.

3 数值结果

s.t.y1+y2≤20+x1-x2，

y≥0．

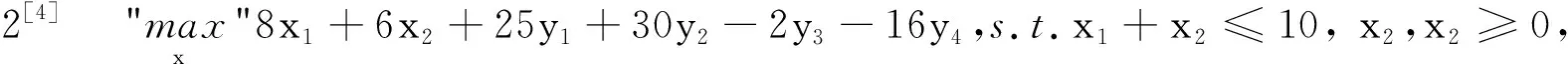
s.t.y1+y2+y3+y4≤10-x1-x2，

-y1+y4≤0.8x1+0.8x2，

y2+y4≤4x2，

y≥0．

不失一般性，取k1=k2=10，γ=10以及α=0.7.数值运算结果见表1，其中L和F分别表示上层决策者和下层决策者的利润.这里，方法1表示本文激励模型，Cao和Leung的部分合作模型用方法2来表示.

表1 激励模型与部分合作模型结果对比

在例1中，(10，0)T是乐观解，140是乐观值.可以看出，本文方法的计算结果与文献[22]的结果是相等的，而且，该结果也与乐观模式的结果相同.

在例2中，(0，2)T是乐观解，232是乐观值.由表1可知，方法1和方法2中下层决策者有相同的收入，然而前者的上层决策者的利润远远大于后者，产生这种情况的原因主要在于，在文献[22]中，除了保证下层决策者的利益最大化外，上层决策者的回报还取决于下层决策者的部分合作程度λ，这种依赖关系在他们的局部合作模型中也有反映.该局部合作模型解决了λ值范围的问题，即只有在给定参数λ的值之后，模型才能得到解决.这毫无疑问会改善和提高下层决策者在决策中的地位，甚至将会把模型固有的上下层递阶关系颠倒过来.

注意到，在本文激励模型中，上层决策者的收益取决于利润分配比例β，虽然它是一个变量，受到下层决策者的影响，但是模型目标仍然是最大化上层决策者的利益，因此，与文献[22]不同的是，上层决策者在决策过程中仍然扮演着主要的角色.

4 结论

本文提出了一个不适定线性二层规划问题的激励模型.这个模型可以激励下层决策者心甘情愿与上层决策者合作，从而使上层决策者的利益最大化.数值结果表明，该方法是切实可行的，并且在保证下层决策者达到同样的最优利益的基础上，本文模型中上层决策者的最终收益优于基于合作度的部分合作模型的上层决策者收益.本文主要针对线性问题，在以后的研究中，将会将激励措施用到非线性问题中，得到相应的理论结果及具体算法.