三角形中的新定义面面观

⦿山东省邹平市梁邹实验初级中学 李光大 张婷丽

在学生掌握三角形基础知识的前提下，进行三角形新定义的探究，不仅能夯实学生有关三角形的基本定理和概念，而且能提升学生运用旧知解决新知的能力，进而发展学生的创新能力.三角形中的新定义问题，包括“和谐三角形”问题，“等角点”问题，“友好三角形”问题，“三分线”问题，“特征三角形”问题，等等.以下结合典例做一做探讨.

1 “和谐三角形”问题

初中阶段学过的特殊三角形有直角三角形、等腰三角形、等边三角形、等腰直角三角形等，它们都有其特殊的性质，且这些三角形因应用广泛而得到推广.这里的“和谐三角形”是指一边上的中线恰好等于这条边的长的三角形.借助“和谐三角形”可考查直角三角形、等腰三角形等的性质，以及学生的知识迁移能力.

例1如果一个三角形有一边上的中线与这边的长相等，那么称这个三角形为“和谐三角形”.

(1)请用直尺和圆规在图1中画一个以线段AB为一边的“和谐三角形”；

(3)如图3，已知正方形ABCD的边长为1，动点M，N从点A同时出发，以相同速度分别沿折线AB-BC和AD-DC向终点C运动，记点M经过的路程为S，当△AMN为“和谐三角形”时，求S的值.

图1

图2

图3

备用图

解析：(1)如图4，①作线段AB的中点O，②以点O为圆心，AB长为半径画圆，③在圆O上取一点C(点E，F除外)，连接AC，BC.△ABC就是所求作的三角形.

图4

图5

(3)易知点M在AB上时，△AMN是等腰直角三角形，不可能是“和谐三角形”；当M在BC上时，连接AC交MN于点E.

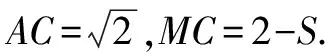
图6

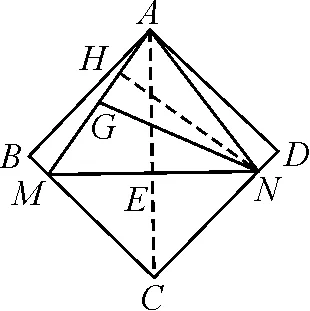
图7

在Rt△AME中，

点评：本题集画图、计算、证明、讨论于一体，综合考查了勾股定理、等腰直角三角形的性质、锐角三角函数等知识，其中第(3)问运用了方程思想和分类讨论思想.

2 “等角点”问题

三角形的内心是指三角形三条角平分线的交点，三角形的重心是指三条中线的交点，三角形的外心是指三边的垂直平分线的交点，三角形的垂心是三条高的交点，三角形的旁心是两条外角平分线与一条内角平分线的交点，它们都是三角形的一些特殊的点，因具有特殊的性质而得到推广.而三角形的的“等角点”是指连接此点与各顶点，所得的三个三角形中有一个三角形与原三角形的三个内角分别相等.当“等角点”与三角形的其他点重合时，会有什么情况发生呢？

例2概念学习：如图8，已知△ABC，点P为其内部一点，连接PA，PB，PC，在△PAB，△PBC和△PAC中，如果存在一个三角形，其内角与△ABC的三个内角分别相等，那么就称点P为△ABC的等角点.

(1)理解应用：根据已学过的知识，下面两个命题是真命题还是假命题？并把判断结果写在后面横线上.

①内角分别为30°，60°，90°的三角形存在等角点..

②任意的三角形都存在等角点..

图8

图9

(2)解决问题：如图9，在△ABC中，∠BAC<∠ABC<∠ACB，点P为△ABC的三个内角的平分线的交点.当点P是等角点时，求△ABC三个内角的度数.

解析：(1)①作内角分别30°,60°,90°的三角形斜边的中线，此中线的中点就是等角点，故为真命题；②在等边三角形中就找不出一点能成为等角点，所以它是假命题，故答案为：真；假.

点评：定义一个新概念，往往都要与旧图形、旧知识联系.本题中的等角点就与直角三角形、等边三角形、三角形内心、三角形内角和、角平分线联系.一方面是因为任何事物都不可能孤立地存在，只有与其他事物联系才有意义；另一方面也是为了考查学生对旧知识的掌握情况.

3 “三分线”问题

三角形的一条中线把这个三角形分成两个三角形，这两个三角形的面积是相等的；三角形一条角平分线分对边所成两条线段的比等于角的两边的比；直角三角形斜边上的中线把直角三角形分成两个等腰三角形.这些都是三角形内特殊的线段.那么，在三角形内画两条线段，能否把一个三角形分成三个等腰三角形呢？

例3教材的习题中有这样的一道题，有一个等腰三角形，它的顶角是36°，把这样的三角形纸片只剪两下，于是得到三个三角形，如何才能使每个三角形都是等腰三角形呢？请画出剪切线，你有多少种方法呢？图10是一个示例.

定义：如果两条线段将一个三角形分成三个等腰三角形，则把这两条线段叫做这个三角形的三分线.

图10

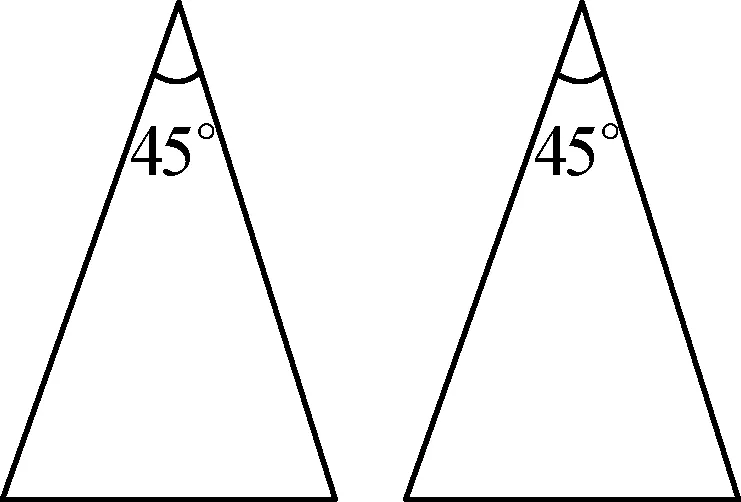
图11

(1)如图11是两个等腰三角形，它们的顶角都是45°，请用不同的方法分别画出这两个三角形的三分线，并求出分得的每个等腰三角形顶角的度数.

(2)△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x，试画出示意图，并求出x所有可能的值.

4 引申变式

引申：如图14，已知正方形ABCD的边长为1，点E在边BC上滑动，若∠AEF=90°，且EF交正方形外角的角平分线CF于点F.当点E滑动到某处时，点F恰好落在直线y=-2x+6上，求此时点F的坐标.

图14

图15

变式如图15，四边形ABCD是菱形，∠ABC=60°，点E是BC边上一点，∠AEF=60°，且EF交直线CD于点F.

(1)求证：AE=EF.

(2)你还能设计出怎样的问题？并尝试解答.

5 结语

几何是初中数学的重点，也是学生学习的难点，书本上的例题、习题都是精心筛选出来的典型题目，教学时需要用好教材又要高于教材，注重习题的变式，挖掘其蕴涵的深层的功效，运用多种思维方法，让学生感悟知识结构之间的关系，既能巩固基本知识、基本模型，掌握知识的本质触类旁通，又能在基础知识上进行拓展，培养学生思维的发散性和深刻性，真正提升学生思维品质.