基于OBLFOA-PP-BC的围岩稳定性二维评价模型

陈光耀,汪明武,金菊良

(合肥工业大学 土木与水利工程学院，合肥 230009)

1 研究背景

围岩稳定性评价一直是工程界关注的问题，特别是近年来随着我国经济社会的飞速发展，相应的工程建设规模也愈发庞大，在公路铁路隧道、水电站和各种矿山建设等工程中，由于围岩稳定性关系到工程建设的安全、设计和施工等诸多方面，故围岩稳定性分类是这类工程建设中的关键问题之一。考虑到围岩稳定性受到诸多因素的控制与影响，且各因素具有多样性、不确定性和可变性的特点，许多学者基于不同的理论探讨了围岩稳定性评价问题，如可变模糊集合理论[1]、粗糙集理论[2]、物元可拓理论[3]、人工神经网络方法[4]、集对分析理论[5]和云模型理论[6]等综合评价方法。但上述方法也存在一定缺陷，例如模糊数学方法实际应用中隶属度函数难以确定；粗糙集理论方法在属性约简过程中可能删掉重要的评价因子；神经网络理论需要大量的样本进行学习，对样本数量和质量要求较高；而集对分析方法存在难以确定差异度系数弊端[7]。

本文尝试将投影寻踪方法 (Projection Pursuit，PP)、果蝇优化算法(Fruit Fly Optimization Algorithm，FOA)和反向学习策略(Opposition-Based Learning，OBL)耦合，针对传统投影寻踪方法最佳投影值的分级阈值难以划分的缺陷，引入了逆向云(Backward Cloud, BC)模型予以改进优化，并引入模糊熵作为描述评价结果模糊复杂程度的辅助参评量，构建了基于反向学习果蝇算法寻优的围岩稳定性逆向云投影寻踪评价模型(OBLFOA-PP-BC)，以提高围岩稳定性的分类可靠性。最后以两个工程实例应用验证了该模型的可行性和有效性。

2 OBLFOA-PP-BC二维评价模型

2.1 投影寻踪法简述

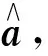
(1)

式中：Sz和Dz分别为投影值标准差和投影值类内密度，计算公式分别为：

(2)

(3)

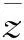
假设有m个样本和n个评价指标，且第i个样本中第j个指标值记为xij，则可得m×n阶数据矩阵X为

(4)

为消除各指标值的量纲，统一各指标变化范围，对样本矩阵X按下列2种情况进行归一化处理。

(1) 对于越大越优型指标有

(5)

(2) 对于越小越优型指标有

(6)

式中：x·jmax和x·jmin分别为样本集中第j个指标的最大值和最小值。若投影方向向量a=(a1,a2,…,an),则第i个样本的投影值zi为

(7)

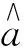
2.2 OBLFOA算法

果蝇优化算法是一种基于果蝇觅食行为的启发式群智能优化算法[10]，具有强大的全局寻优能力、较小的计算量和较低的复杂度等优点[11-12]，且原理简单清晰、不依赖求解问题的具体信息并具有优秀的易耦合性。目前，已有学者利用FOA与其他方法耦合得到了性能更加出色的混合算法[13-14]并成功应用于相关领域，但传统FOA仍存在着局部寻优能力不足、寻优结果不稳定和易过早收敛等问题。为克服这些缺陷，本文基于反向学习概念和精英种群策略改进优化FOA，并用于PP方法中投影指标函数最大值Q(a)的求解。

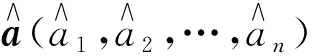
(8)

(9)

(11)

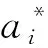
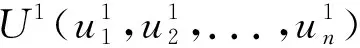
(12)

(13)

(4)进入迭代，重复步骤(1)—步骤(3)可得第t迭代次数下的种群矩阵Xt和精英种群Et。

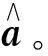
2.3 OBLFOA算法测试

由于利用反向学习策略改进FOA尚未有先例，故为验证OBLFOA相较于传统FOA的优越性，本文采用了12个标准算法优化测试函数进行测试，测试函数在算法中的搜索参数设置详见表1。

表1 标准测试函数Table 1 Benchmark test functions

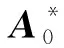
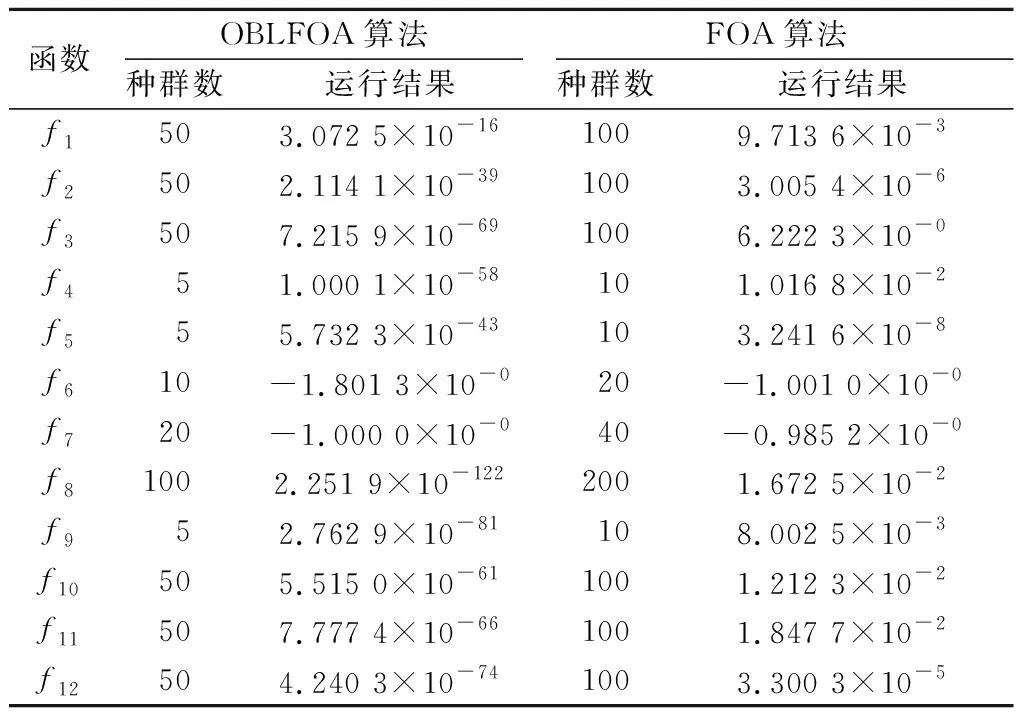
表2 OBLFOA和FOA在不同测试函数中的运行结果Table 2 Running results of OBLFOA and FOA indifferent benchmark test functions

由图1中12种测试函数收敛情况可见，OBLFOA无论是在收敛精度还是收敛速度上均优于传统FOA，故采用反向学习和精英种群策略用于对FOA改进优化是有效可行的，且效果良好。

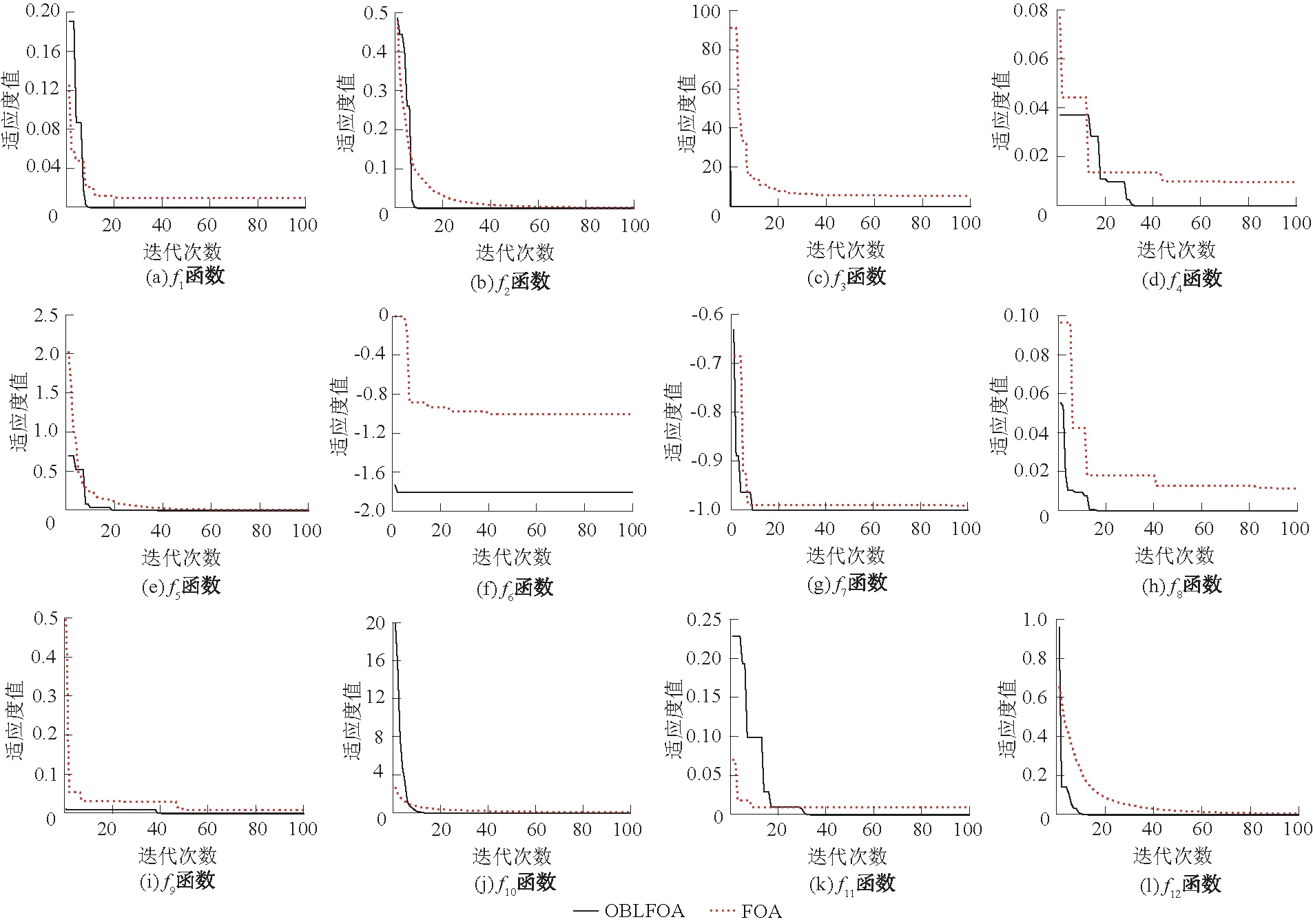
图1 OBLFOA和FOA测试函数收敛曲线Fig.1 Convergence curves of test functions’ fitness of OBLFOA and FOA

2.4 OBLFOA-PP-BC评价流程

基于OBLFOA-PP-BC的二维围岩稳定性评价流程如图2所示。具体流程如下所述。

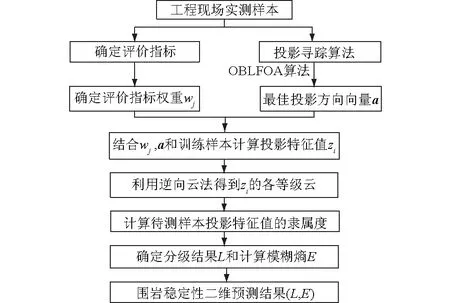
图2 OBLFOA-PP-BC围岩稳定性评价流程Fig.2 Flow chart of OBLFOA-PP-BC model forsurrounding rock stability evaluation

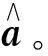
(2) 确定评价指标权重wj。权重反映出各个指标在评价过程中的贡献程度，为客观挖掘出样本实际指标信息，本文采用熵权法确定权重，其主要计算方法为:

(14)

(15)

(16)

式中：wj为第j项指标权重；ej为第j项指标熵值；1/lnn为信息熵系数；P=(pij)n×m是归一化后标准矩阵。

(17)

(18)

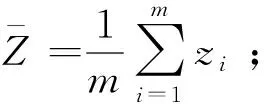
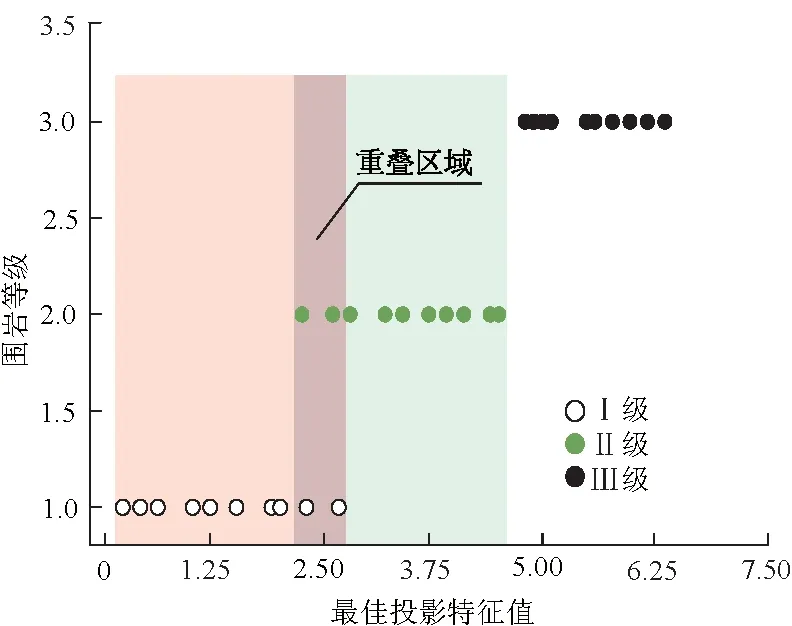
图3 阈值划分示意图Fig.3 Threshold partition

(19)

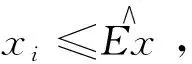
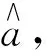
式中：μi为围岩预测样本在第i等级的隶属度；S为标准化系数，一般取1/(nln2)；规定0ln0=0。

根据文献[21]的相关讨论，当E越接近1，则模糊性越大，结果越难评价；当E越接近0，则模糊性越小，结果越易评价。故将围岩稳定性评价的等级归类复杂模糊程度与E的对应关系规定为：[0,0.25)、[0.25,0.5)、[0.5,0.75)和[0.75,1]，分别对应为清晰、较清晰、较模糊和模糊。

(7) 最后按最大隶属度原则判定围岩稳定性归类结果L，并和模糊熵E在等级和评价复杂性2个方面共同组成围岩稳定性二维评价结果(L,E)。

3 应用实例

由于影响围岩稳定性的指标多达十几个[23]，并且不同工程实践中对于指标选取方式也不相同，故为验证模型的通用性和有效性，本文选取文献[22]和文献[23]中工程实测样本数据分别作为实例1和实例2，并对其待测样本围岩稳定性进行计算评估与对比分析。

3.1 实例1

根据文献[22]中煤矿企业提供的相关数据，并参考围岩分级评价体系选取了天然单轴抗压强度(Nu)、饱和单轴抗压强度(Su)、软化系数(K)、天然抗剪强度(Ns)、饱和抗剪强度(Ss)、含水率(Mc)和岩石质量指标(Rq)7项指标作为评价因子，将煤矿巷道围岩稳定性主要分为Ⅰ级(稳定)、Ⅱ级(较稳定)和Ⅲ级(不稳定)3类，故该实例为七元三分类问题。样本实测值如表3所示，其中前22组为训练集，余下8组为测试集(编号用“*”标出)，由于篇幅有限，训练集只列出部分，详细数据可前往文献[22]查阅。

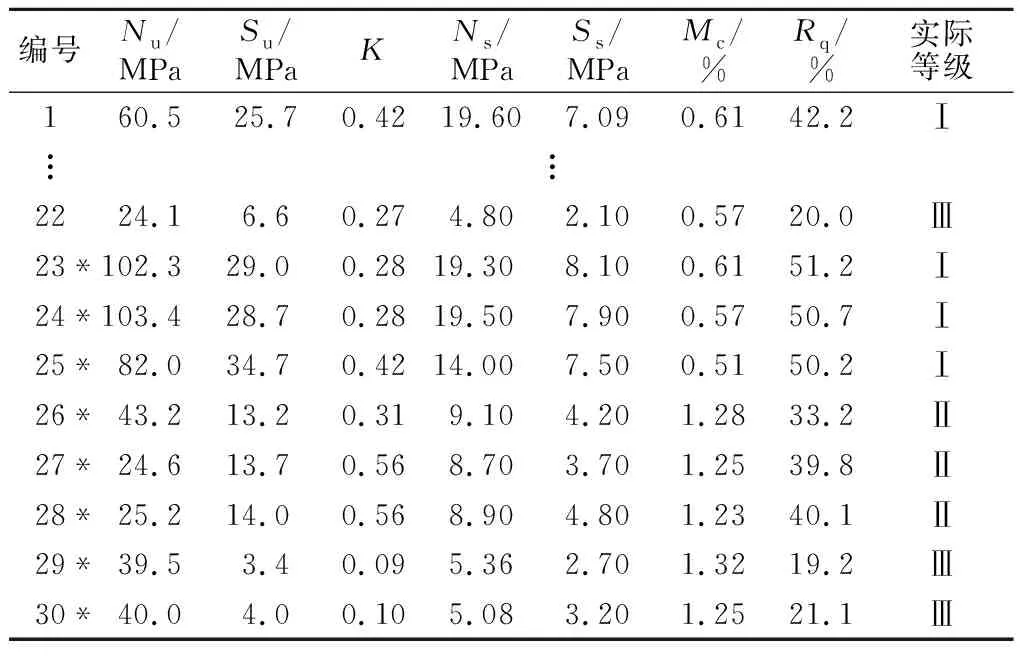
表3 实例1的训练样本和测试样本数据Table 3 Training samples and test samples of case 1

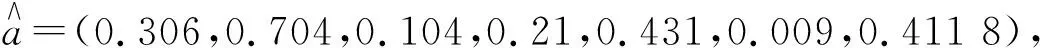
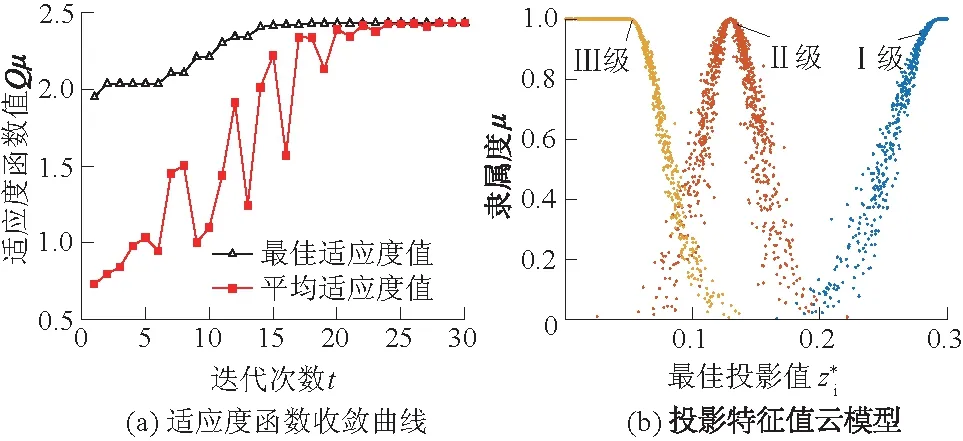
图4 实例1的适应度函数收敛曲线和投影特征值云模型Fig.4 Convergence curve of fitness function andthe cloud model of projection values for case 1

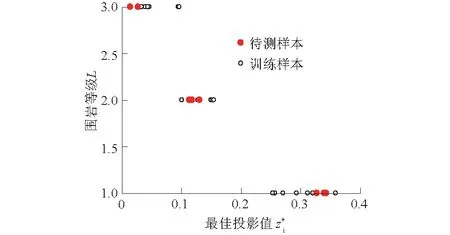
图5 实例1样本集最佳投影值与等级L的散点图Fig.5 Scatter plot of projection values andgrades yi for sample set of case 1

由表4评价结果可见，本文方法相较于BPNN、随机森林和SVM 3种机器学习方法分级准确确率更高，且模糊熵值可反映出待测围岩样本评价结果的演变趋势，如编号为23*、24*、25*、28*、29*和30*的待测样本模糊熵计算值均<0.25，故可判定该6个待测样本的评价结果清晰可靠；而编号27*样本模糊熵为0.502 1，属于评价较模糊区间，虽然本文方法将其判定为Ⅱ级围岩，但隶属度μ(Ⅱ)和μ(Ⅲ)的值可反映出该样本是有偏向Ⅲ级围岩趋势的，同理编号26*样本亦如此。而BPNN、随机森林法和SVM的预测结果也可侧面验证这一点：在对模糊熵<0.25的待测样本预测上，本文方法和以上3种方法预测结果均相同；而对模糊熵>0.25的待测样本预测上，4种方法的预测结果却出现分歧。由于引入了模糊熵E作为辅助参评量，故本文方法在围岩稳定性评价复杂程度描述上相较于其它方法更有优势；引入逆向云算法则可综合考虑评价过程中的随机性和模糊性，不仅避免了边界点重叠难以划分阈值的困扰，还令评价结果相对更加客观准确。

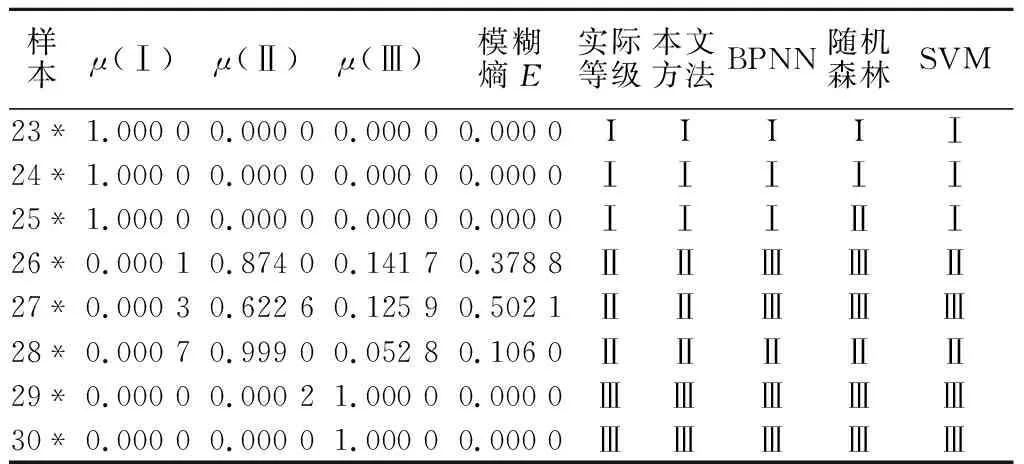
表4 实例1的隶属度和评价结果对比Table 4 Membership degree and comparison ofevaluation results for case 1

3.2 实例2

围岩稳定性分级指标体系目前基本是以岩石单轴饱和抗压强度、完整性系数、岩石质量指标(RQD)和结构面特征等参数作为评价指标，且基本都是围岩揭露后进行的工作，而将围岩声波指标及弹性参数作为围岩稳定性评价指标则少之又少。为此，实例2选取了文献[23]中利用TSP303系统对成昆铁路邓家湾隧道围岩采集解译出的纵波速度(X1)、横波速度(X2)、纵横波速比(X3)、泊松比(X4)、密度(X5)和静态杨氏模量(X6)6项参数作为围岩稳定性评价指标，并对该隧道的另外10个待测样本进行评价。具体样本数据见表5，其中编号1—40为训练样本，剩余10组(编号用“*”标出)为待测样本。

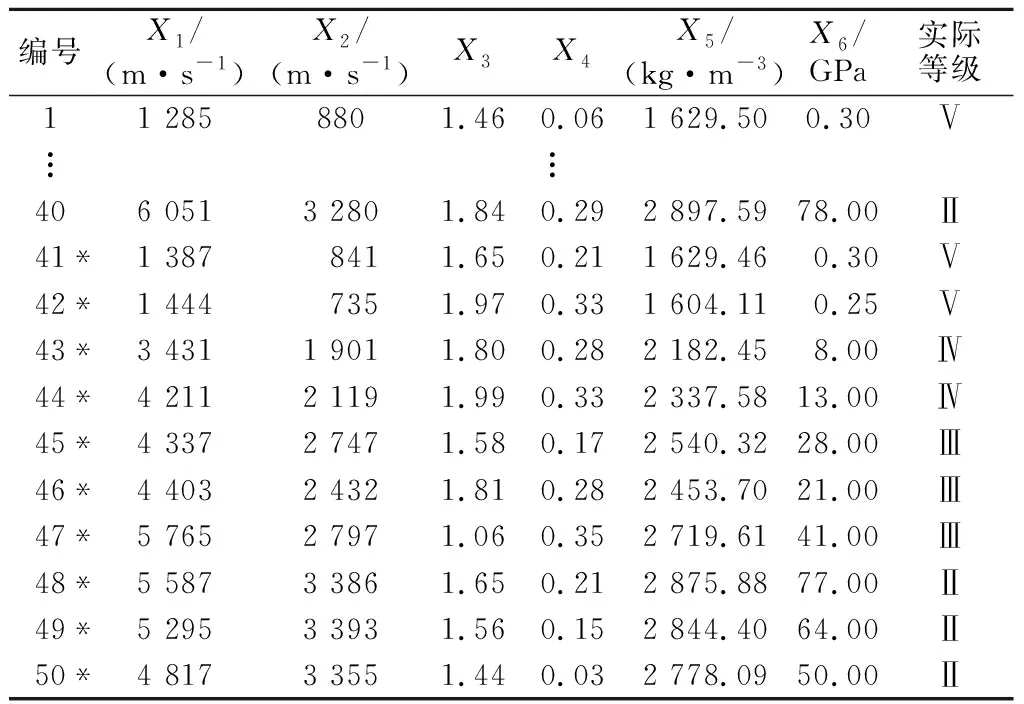
表5 实例2的训练样本和测试样本数据Table 5 Data of training samples and test samples ofcase 2

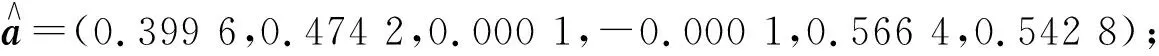
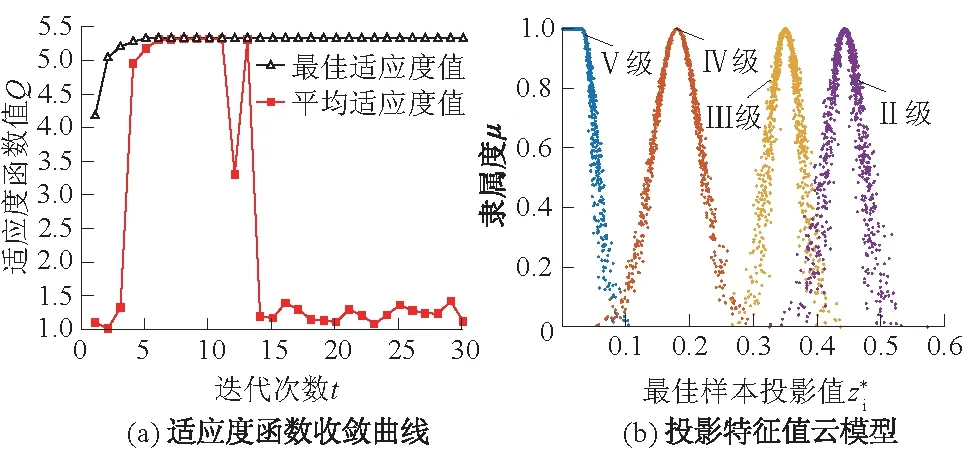
图6 实例2的适应度函数收敛曲线和投影特征值云模型Fig.6 Convergence curve of fitness function and cloudmodel of projection charactistic values for case 2

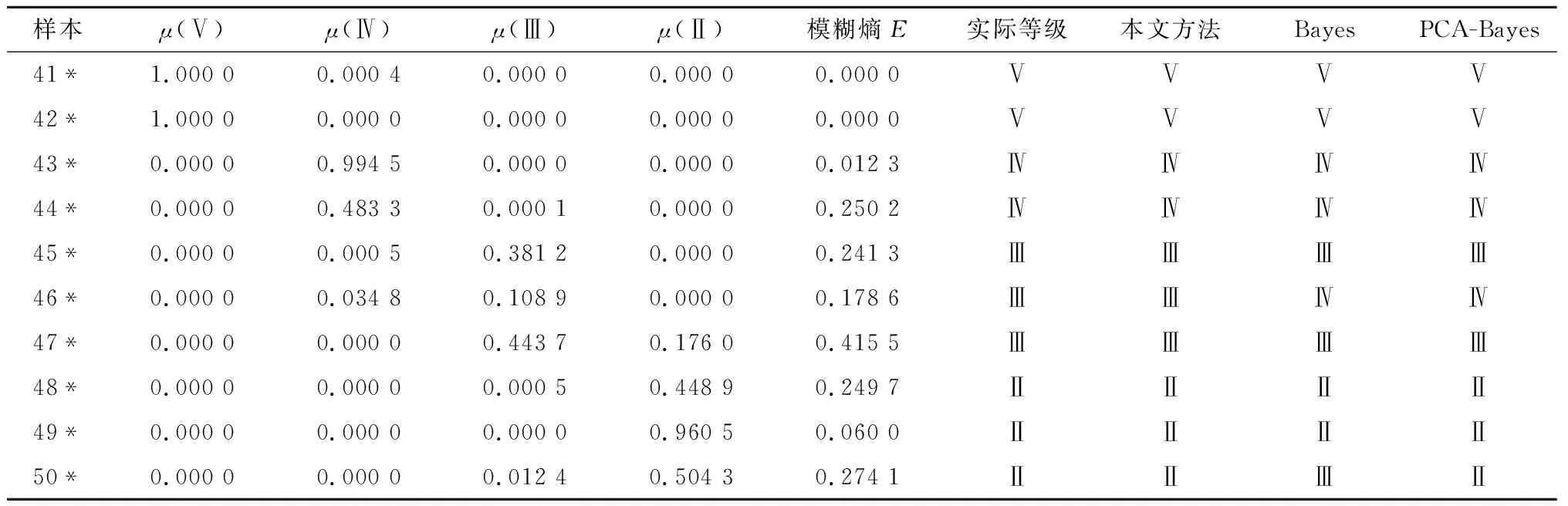
表6 实例2的隶属度和评价结果对比Table 6 Membership degree and comparison of evaluation results for case 2

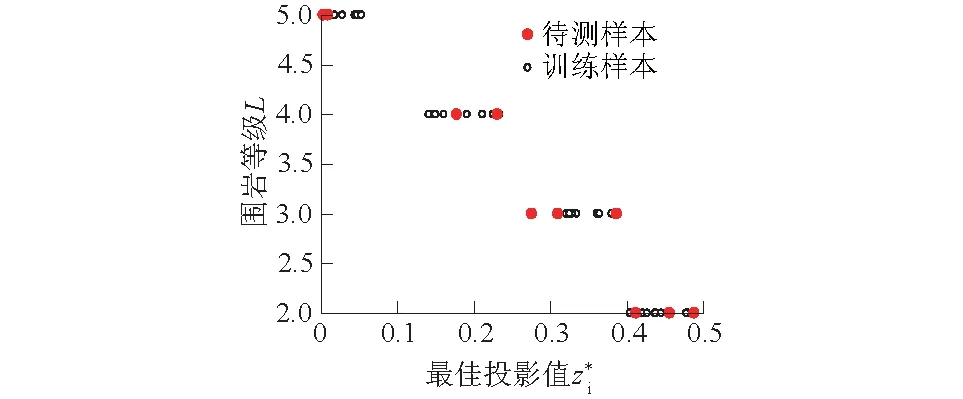
图7 实例2样本集最佳投影值与等级L的散点图Fig.7 Scatter plot of projection values versusgrades L for sample set of case 2

由表6可见，本文方法最终评价结果和待测样本实际围岩等级吻合，相较于文献[23]中PCA-Bayes法评价的评价准确率更高。

4 结 论

(1)首次提出了基于反向学概念生成反向种群并结合精英种群策略的改进果蝇优化算法OBLFOA，并和传统FOA一同对12个标准算法优化测试函数进行收敛精度和收敛速度的对比测试，结果表明OBLFOA算法在生成反向种群和精英种群策略的改进下，大大加快了算法的收敛速度并提高了收敛的精度。

(2) 针对投影寻踪方法在相关评价问题的应用中会出现最佳投影特征值的分级阈值难以划分的情形，提出了将计算出的样本最佳投影值通过逆向云算法构建出不同等级下的最佳投影值正态云模型，成功将阈值划分难题转化为对待测样本隶属度的定量计算，进而有效解决了投影寻踪方法中分级阈值难以划分的问题。实例应用表明，该方法过程清晰、计算简单且便于应用。

(3) 考虑到工程现场各指标在评价过程中的贡献程度不同，为便于应用，本文仅采用熵权法计算出各评价指标的客观权重，而未考虑可根据专家经验知识确定的主观权重。因此，在指标的权重确定仍有待改进优化。

(4)针对围岩稳定性评价是一个具有多因子相互影响的随机不确定非线性问题，本文引入模糊熵概念作为围岩稳定性评价的辅助参评量，用以描述待测样本评价结果可靠度和评价过程的模糊复杂程度。实例应用表明，模糊熵可以有效反映出围岩评价结果可靠度和演化趋势。

针对影响围岩稳定性评价的因素众多且评价指标体系并不唯一，本文选取了2个采用不同评价指标体系的工程实例对本文方法进行应用验证。实例应用结果表明，本文方法应用于围岩稳定性评价有效可行，为围岩稳定性分级等相关评价问题提供了新的参考。