裸露穿河管道在压重块保护下的冲刷特性
2022-04-16杨庆华王子聪张宇倩
杨庆华,王子聪,杨 乾,3,张宇倩
(1.西南交通大学 土木工程学院,成都 610031; 2.中国三峡建工(集团)有限公司,成都 610041;3.中国五冶集团有限公司,成都 610063; 4.彭州市水务局,成都 611930)
1 研究背景
作为国家能源大动脉,我国油气长输管道总里程已经达到13.9万km[1]。水下穿越作为管道过河的主要形式,需要将管道敷设在具有一定设计埋深的河床之下,但是由于河床变形、人工采砂等因素,极易造成管道的裸露[2]。严重情况下还易使管道发生断裂破坏,从而造成巨大的经济损失和环境污染[3]。一般来说,工程在水下穿越管道裸露之后需采用压重块保护措施以保证其自身的稳定性,并防止管道被水流冲刷漂浮后发生断裂破坏。目前,水下穿越管道在压重块保护措施下的冲刷特性还不明确,河床地形变化的不确定性仍给管道的安全运行造成了威胁[4]。因此,研究水下穿越管道在压重块保护措施下的冲刷特性具有十分重要的意义。
目前,国内外学者对水下穿越管道主要开展了如下3个方面的研究。
(1)在无压重块保护措施下管道的冲刷研究。Mao[5]、Chiew[6]提出了波浪作用下海底管道最大冲刷深度的计算模型;刘延鑫等[7]、陈兵等[8]采用数值模拟的方法对水下穿越管道的冲刷流场进行了分析,为管道的局部冲刷机理研究提供了理论基础;杨乾等[9-10]对水下穿越管道的局部冲刷机理做出进一步研究,得出了管道冲刷深度的预测公式。
(2)在有压重块保护措施下管道的受力研究。胡玉霞等[11-12]通过拖箱试验,对比了海底无压重块保护措施和有压重块保护措施的管道水动力荷载,得出了压重块保护措施下管道水动力荷载随KC数变化的规律;李俊[13]、于淼[14]通过分析管道在不同工况水流冲刷下的受力特点,提出了压重块布置间距的优化算法;杨景威等[15]、陈利琼等[16]采用力学分析软件对加压重块管道的应力变化过程进行了分析,得出管道应力分布随压重块布置间距变化的规律。
(3)在有压重块保护措施下水下穿越管道的冲刷研究。马良[17]通过对海底管道在压重块保护措施下悬空长度的理论分析,得到压重块最大允许布置间距的计算表达式;刘颖等[18]则通过分析管道悬空长度和共振频率的关系,对管道悬空长度做出进一步限制,为水下穿越管道的压重块保护措施设计提供了理论基础。
综上所述,现阶段国内外对压重块保护措施下管道的冲刷特性研究主要集中在海底管道。而海底管道与内陆河道中的水下穿越管道不同,海洋流场复杂多变,管道冲刷受波浪、潮流等因素共同影响,相反内陆河流中这方面的影响却较小,因此两者的冲刷情况不同。此外,在压重块保护措施下水下管道的冲刷研究中,学者们主要对管道的悬空长度进行了计算讨论,对管道周围河床的冲刷扩展情况和冲刷深度分析还不够充分。基于此,本文通过开展水槽模型试验,对不同压重块布置形式下管道的冲刷特性进行研究,探究压重块长度、压重块布置间距、水流流速、河道水深等因素对管道周围河床冲刷地形和冲刷深度的影响。
2 模型设计
2.1 试验比尺
试验中模拟河道的水流为明渠流,重力和惯性力起主导作用,因此采用重力相似准则,其表达式为
(1)
式中:λv为流速比尺;λl为几何比尺;λg为重力加速度比尺(λg取值为1)。
根据《输气管道工程设计规范》[19]的规定,常用穿河输气管道外径范围为219~3620 mm。结合实际的试验场地条件,取几何比尺λl为25,采用外径30 mm的有机玻璃空心圆管作为试验管道模型。由几何比尺λl推算得出的其他试验相关比尺参数如表1所示。
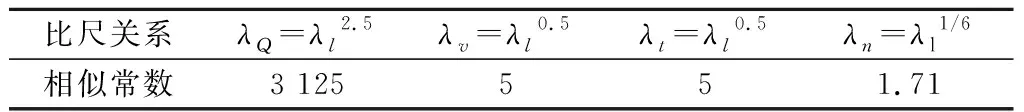
表1 试验主要比尺参数Table 1 Main scale parameters of the test
2.2 试验装置
试验地点位于西南交通大学市政工程流体力学实验室,采用长9.1 m、宽0.4 m、高0.7 m的单向循环水槽。为便于对管道的冲刷过程进行观测,水槽侧壁采用透明钢化玻璃。水槽前端利用梯形堰控制流量(流量通过读取堰流水深h1,并利用梯形堰计算公式求出),设置稳流板为试验段提供均匀流。水槽的末端设置有尾门,便于控制试验设计水深h2。试验段位于水槽的中下游,其布置如图1所示。试验段全长120 cm,铺沙段长度60 cm,沙床厚度为10 cm。沙床两端各设有长度为30 cm的碎石缓冲段,以防止沙床被冲塌,缓冲段碎石的中值粒径为1 cm。模拟管道垂直于水流方向布置于试验段中部,两端与水槽边壁固定,处于半埋裸露状态。压重块布置在管道上,其两端埋在沙床中,埋深为1.5 cm。
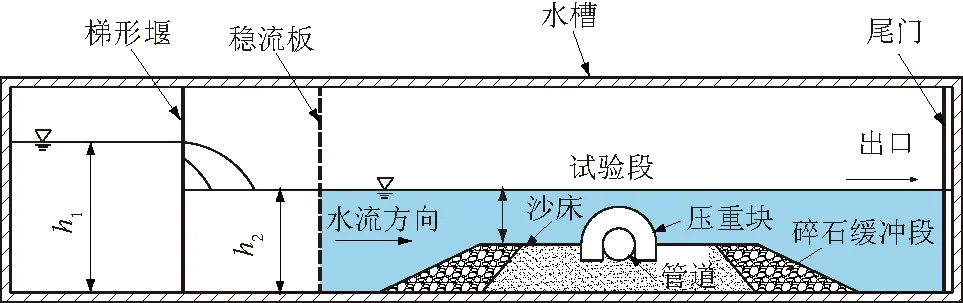
图1 水槽试验段布置Fig.1 Layout of the flume test section
2.3 试验模型沙和压重块
按《水电水利工程常规水工模型试验规程》[20]的规定,模拟砂砾石河床覆盖层,宜采用碎石散粒体,其粒径按照长度相似换算选择。试验选择石英沙作为模型沙,根据实际勘察得到的河床砂砾石粒径分析结果,按照试验的几何比尺换算,得到如图2所示的沙颗粒级配曲线。由沙颗粒级配曲线可知,沙颗粒的粒径分布比较均匀,主要集中在0.3~0.7 mm之间。沙颗粒的中值粒径d50为0.55 mm。
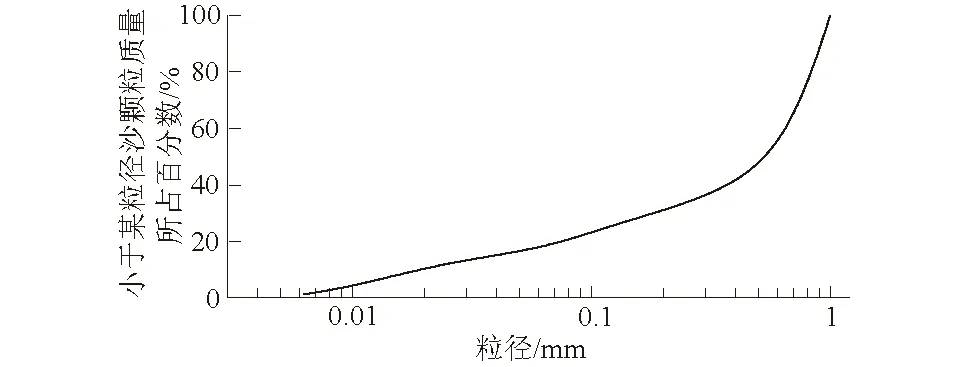
图2 沙颗粒粒径分布曲线Fig.2 Gradation curve of sand particles
压重块的形式为马鞍形,根据《石油地面工程设计手册》(第五册)[21]规定,马鞍形压重块与管身结构设计的质量比为1.34~1.52,经过分析计算取压重块壁厚δ为20 mm。压重块长度Lm分别取4、6、8 cm,试验过程中压重块的布置间距Ln可以调整,其布置示意图如3所示。
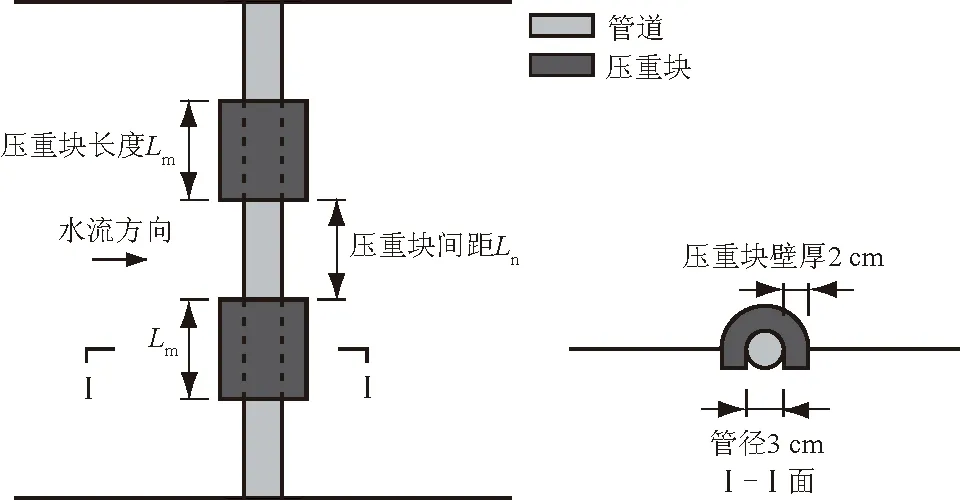
图3 压重块布置Fig.3 Layout of heavy block
2.4 试验测点和工况
试验使用的ADV型号为Vectrino Profiler,其距离测量功能可以用于测量试验段的地形。为保证测量的地形数据具有可靠性,在管道周围布置较密测点。顺水流方向布置7个测量断面,断面间距5 cm,每一断面上布置15个测点。测点间距2 cm,其中最外侧测点距离试验水槽侧壁的距离为6 cm,试验段地形测点及试验段仪器布置如图4所示。
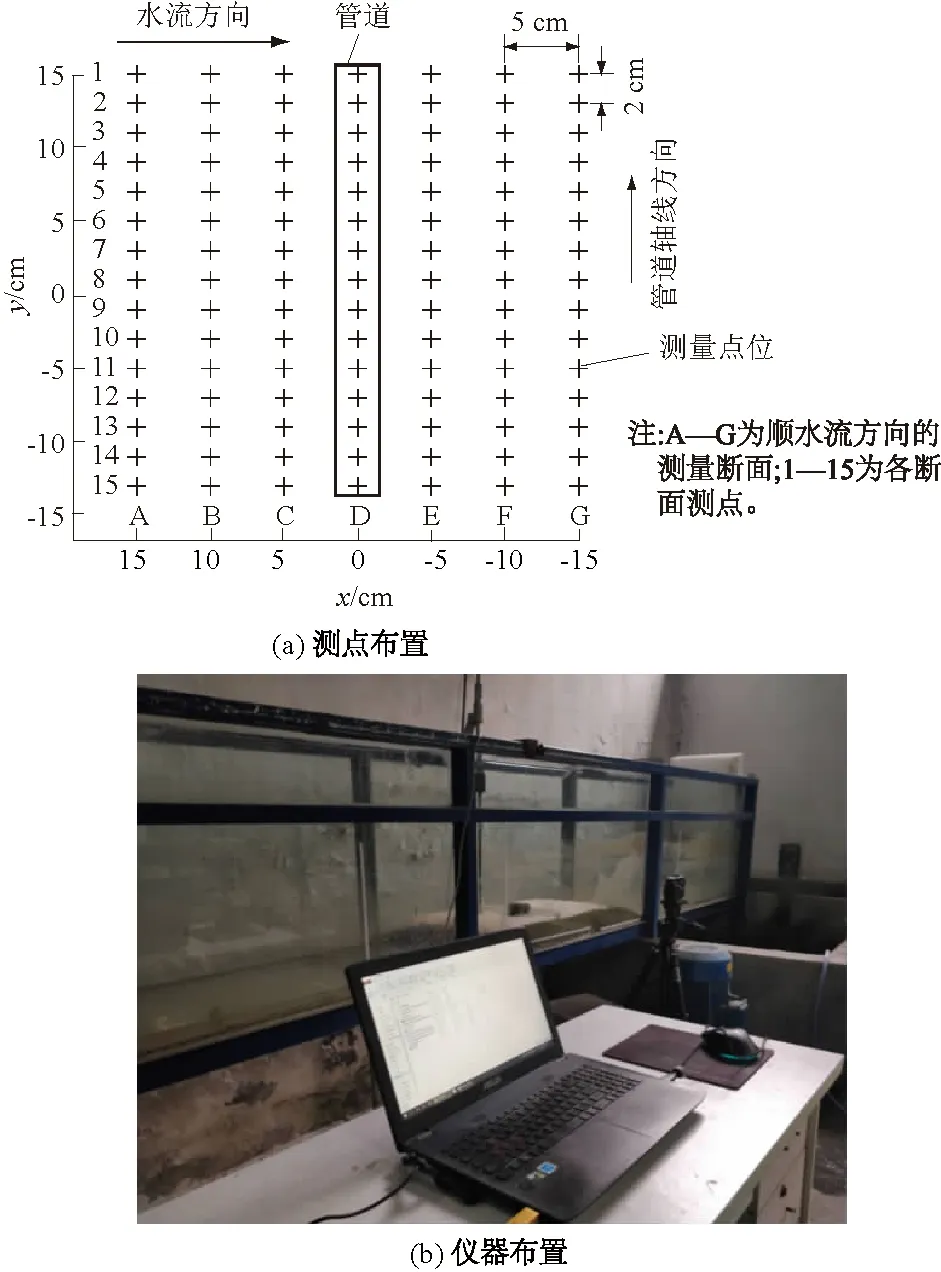
图4 试验段测点及仪器布置Fig.4 Layout of measuring points and instrumentin the test section
压重块适用于中小型穿越河段裸露管道的保护,结合试验水槽实际宽度,所研究河道模型宽度L取40 cm。试验中需要分析压重块长度Lm和布置间距Ln对管道在水流作用下冲刷特性的影响,为方便研究,取压重块长度与河宽比值Lm/L为压重块长度系数,其值分别为0.10、0.15、0.20。取压重块布置间距与压重块长度比值Ln/Lm为压重块间距系数,其值分别为1、2、3。采用泥沙起动流速计算公式[22]得到试验模型沙的临界起动流速Vc=0.20 m/s,选择3种不同的流速,分别为Vc的1.25、1.5、2.0倍,即0.25、0.30、0.40 m/s。根据试验水泵可以提供的最大流量,模拟河道设计水深h分别取8、10、12 cm,试验的全部9组工况如表2所示。文献[10]中已对流速分布进行了验证,水槽断面和河床初始冲刷断面的流速分布比较均匀,满足试验段所需均匀流的要求。试验主要研究中间管道段和压重块的局部冲刷深度,距离水槽边壁较远,可以忽略试验边界的影响。
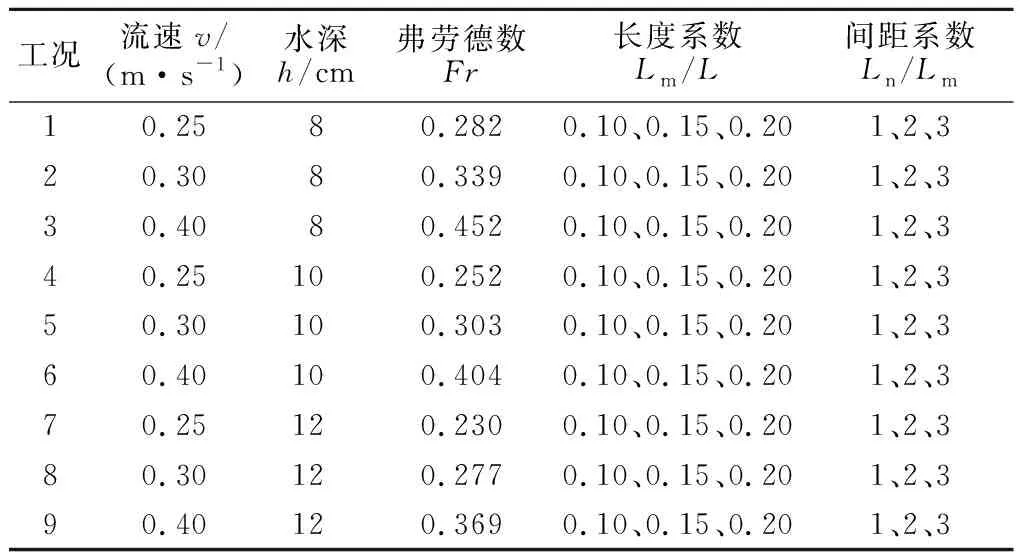
表2 试验工况组合Table 2 Factors of the orthogonal test
试验开始前,先将ADV的测量探头固定在试验段的可滑动杆件上,然后把ADV的传感器连接到计算机上。当管道和压重块布置完毕后,打开水泵,关闭水槽尾门,缓慢调节水泵阀门,使水流缓慢浸润沙床。为避免在调整流量过程中对河床产生冲刷影响,试验时先保持尾门关闭,缓慢打开阀门,以很小的入流量蓄满水槽。待模拟河道段水位达到(2.0~2.5)h时,调整阀门至设计流量,再缓慢打开尾门,调节模拟河道水深降低至设计值h,这样便能避免试验过程中对河床产生试验准备所引起的局部冲刷。待管道周围河床冲刷开始后,移动ADV的测量探头读取试验测点的地形数据。以此类推,直到所有工况下的测点地形数据均被采集完毕试验结束。
3 试验结果分析
3.1 试验现象分析
3.1.1 地形变化过程
经过试验观察发现,所有工况中加压重块管道在水流作用下的冲刷地形变化过程比较相似。根据管道附近河床地形变化的程度,整个冲刷过程可以分为4个阶段,分别为冲刷坑形成、压重块迎流侧悬空、管道迎流侧悬空和冲刷平衡,各阶段的地形等高线如图5所示。管道中心所在的水平面为管道中心平面,图5中等高线“+”表示河床地形高程点高于管道中心平面,而“-”则表示河床地形高程点低于管道中心平面。
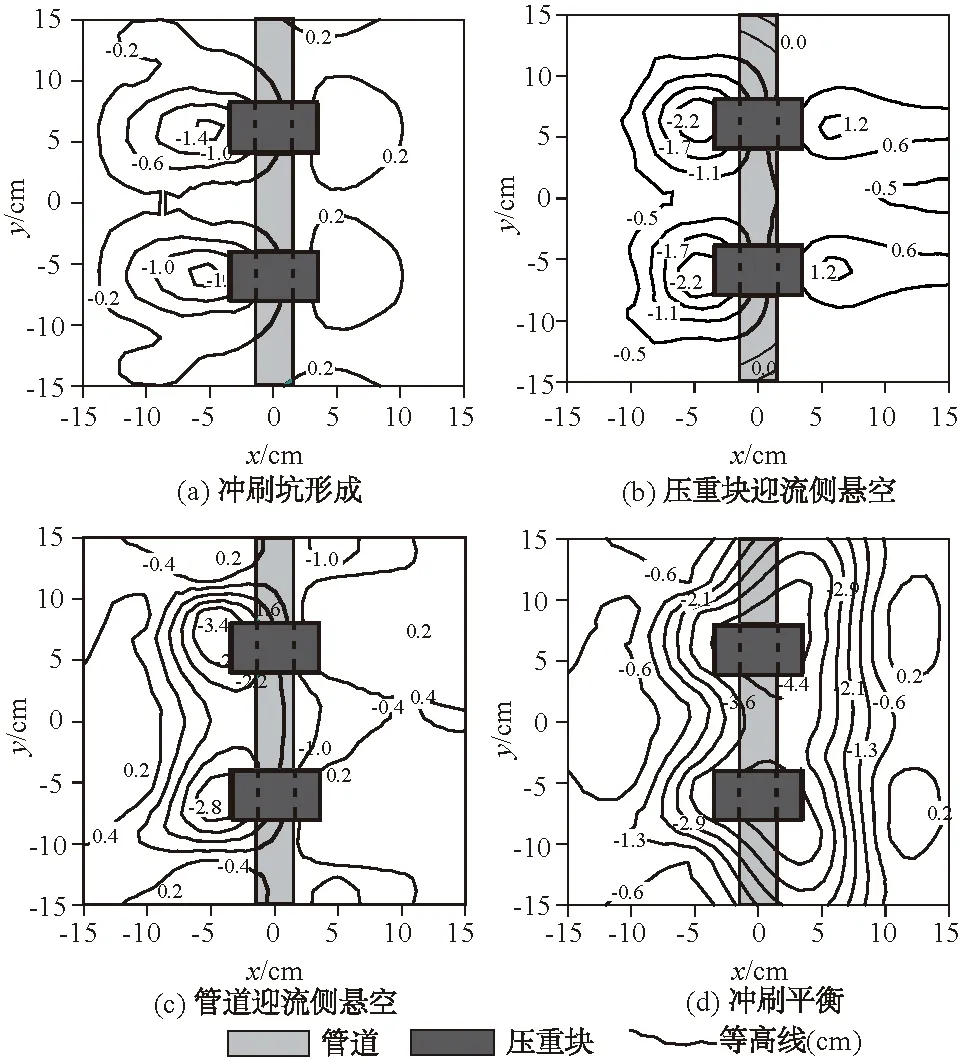
图5 管道冲刷的4个阶段Fig.5 Four stages of pipeline scour
(1)冲刷坑形成。在水流作用下,压重块的迎流侧会形成冲刷坑,随后沿管轴向两侧扩展。压重块迎流侧的沙颗粒被水流挟带着转移到压重块的背流侧,同时管道上游河床中的沙颗粒也有部分被转移到管道的下游河床,使得管道下游河床整体升高。
(2)压重块迎流侧悬空。随着冲刷坑深度的增加,压重块的迎流侧被水流逐渐冲刷至悬空状态。在此过程中冲刷坑继续沿管轴向两侧扩展,并与另一边压重块的冲刷坑合并形成较大的冲坑。另外,压重块背流侧的沙颗粒持续堆积形成沙坡,并且有少部分沙覆盖在压重块之上。
(3)管道迎流侧悬空。在水流作用下,压重块迎流侧的沙颗粒被持续冲刷带走,直到管道悬空。压重块与管道背流侧的沙坡高度也开始降低,并逐渐形成冲刷坑。当压重块和管道背流侧冲刷坑的深度到达某一临界值时,将会与迎流侧的冲刷坑形成连通冲坑。
(4)冲刷平衡。经过较长时间的冲刷后,管道中心距河床面的冲刷深度保持不变,达到冲刷平衡状态。压重块背流侧的沙颗粒也被完全冲走,管道与压重块的迎流侧和背流侧均处于悬空状态。
3.1.2 管道局部冲刷过程
通过对压重块保护措施下管道局部冲刷过程的观察定性分析, 可以得到其在冲刷坑形成、 压重块迎流侧悬空、 管道迎流侧悬空及冲刷平衡4个冲刷阶段下附近河床的演变几何形态和冲刷特征如表3所示。
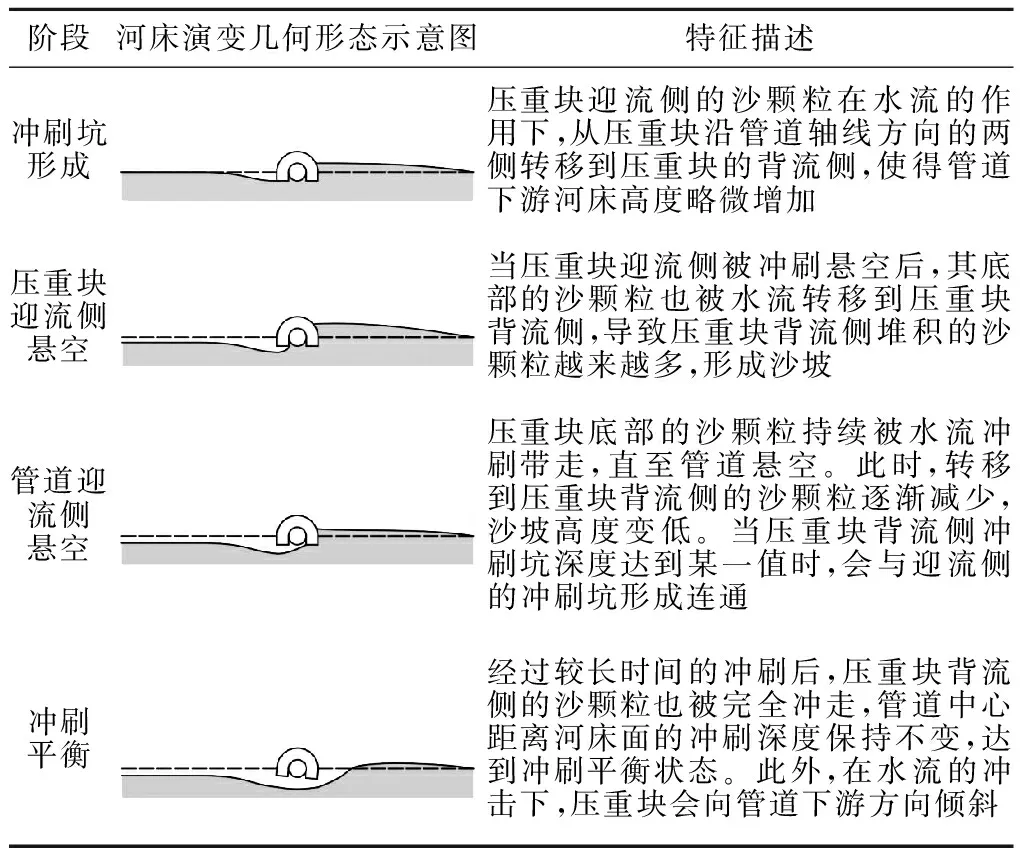
表3 河床演变的形态和特征Table 3 Morphology and characteristics of riverbedevolution
3.2 水动力条件对管道冲刷深度的影响
3.2.1 流速对管道冲刷深度的影响
杨乾等[9]的研究结果表明,弗劳德数Fr作为反应水流缓急程度的无量纲数,能够同时体现出流速和水深对管道底部冲刷坑深度的影响。当管道迎流侧冲刷悬空后,其底部冲刷坑将沿竖向不断扩展,冲刷坑深度随冲刷时间逐渐增大。管道的冲刷深度是管道中心距河床表面的竖直距离,根据试验数据可以绘制出不同流速下管道冲刷深度随时间变化的曲线,如图6所示。管道底部的冲刷坑会以一个极快的速率进行竖向扩展,然后逐渐趋于稳定。管道最大冲刷深度是河床达到冲刷平衡状态后管道中心距河床面的最大竖直距离。由图6可见,在压重块长度系数、压重块间距系数、水深一定时,管道最大冲刷深度随着冲刷流速V和弗劳德数Fr的增加而增加,管道底部河床达到冲刷平衡的时间则随着冲刷速度V的增加而减小。
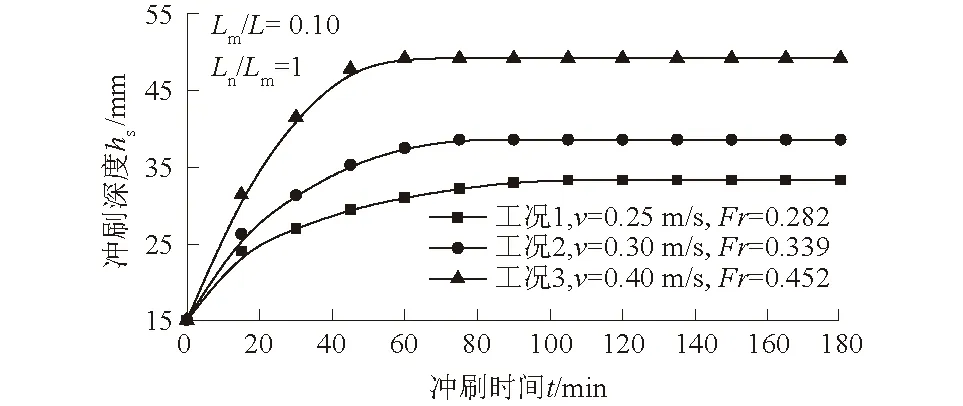
图6 不同流速下管道冲刷深度变化曲线Fig.6 Curves of pipeline scouring depth underdifferent flow velocities
3.2.2 水深对管道冲刷深度的影响
根据试验数据可以绘制出不同水深下管道冲刷深度随时间变化的曲线,如图7所示。由图7可见,在压重块长度系数、压重块间距系数、流速一定时,随着水深h的增加和弗劳德数Fr的减小,管道的最大冲刷深度呈递减趋势。此外,在模拟河道水深h增加的过程中,管道底部河床达到冲刷平衡状态的时间保持不变。
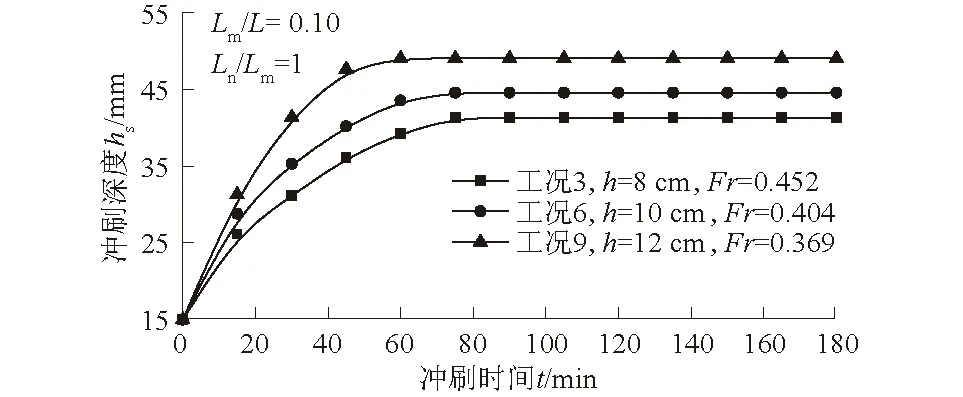
图7 不同水深下管道冲刷深度变化曲线Fig.7 Curves of pipeline scouring depth under differentwater depths
3.3 压重块对管道冲刷的影响
3.3.1 压重块布置间距对管道冲刷的影响
管道附近河床冲刷达到平衡状态后,根据试验所测得的地形数据可以绘制出管道附近的地形等高线,如图8所示。图8为弗劳德数Fr=0.282且压重块长度系数Lm/L= 0.10时管道附近河床达到冲刷平衡状态的地形图。由图8可见,随着压重块间距系数增加,管道附近河床的整体冲刷深度呈现减小趋势。平均冲刷深度是一段管道冲刷深度的平均值,管道段分为布置有压重块的管道段和未布置压重块的管道段。压重块间距系数从1增加到3的过程中,未加压重块管道段的平均冲刷深度减少了10%,而加压重块管道段的平均冲刷深度则减少了15%。经过对比发现,加压重块管道段的平均冲刷深度总是比未加压重块管道段的平均冲刷深度高30%~40%。这是因为压重块对水流的阻挡作用使得加压重块管道段底部的冲刷流速高于未加压重块的管道段,从而导致加压重块管道段的平均冲刷深度偏高。
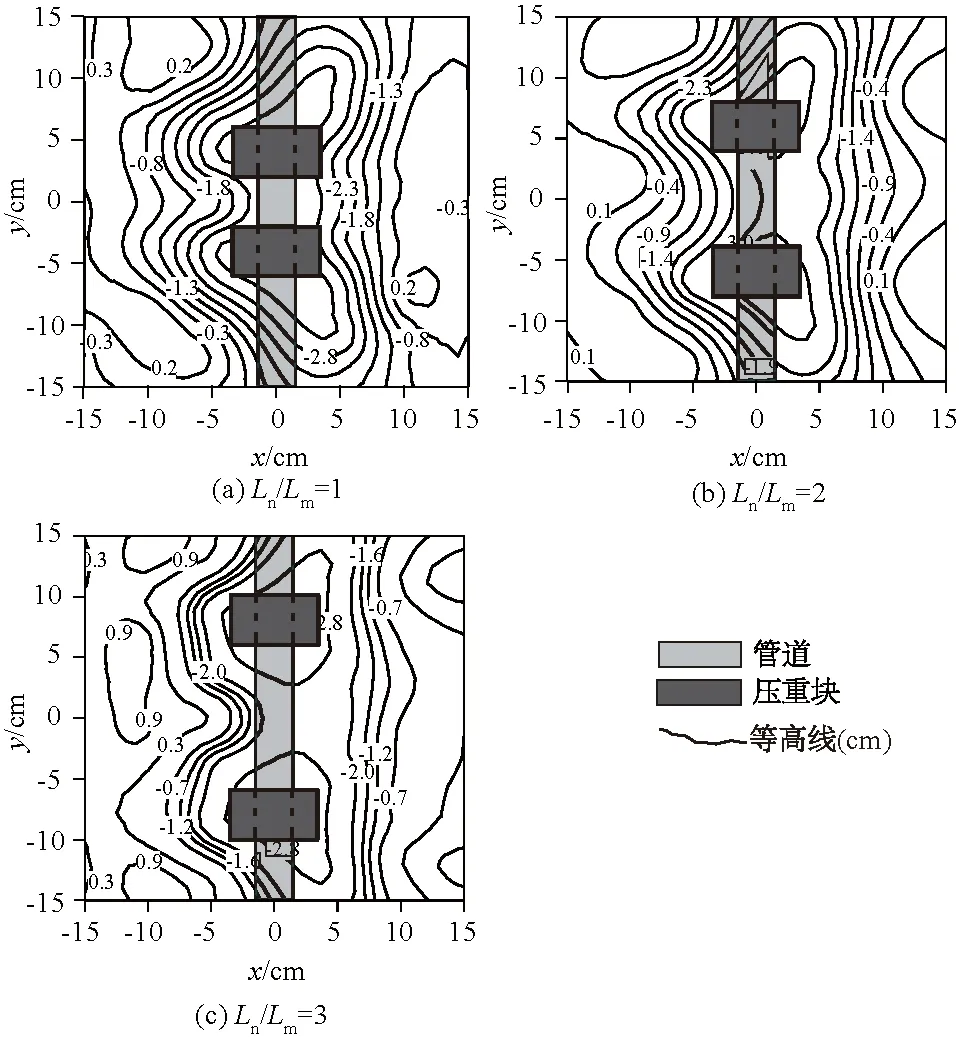
图8 压重块布置间距变化时冲刷地形Fig.8 Topographic map of scouring in the presence ofvaried spacings between heavy blocks
从河床的地形起伏变化情况来看,管道迎流侧的冲刷深度普遍要高于其背流侧。这是由于在冲刷的初始阶段,少部分管道迎流侧的泥沙被水流转移到其背流侧,使得管道背流侧河床整体升高。此外,随着压重块布置间距的增加,管道下方冲刷坑面积虽然逐渐增大,但是冲刷深度却在逐渐减小,这表明压重块之间相互作用对河床冲刷的影响在逐渐减弱。根据测量的地形数据可以绘制出不同压重块布置间距下管道冲刷深度随时间变化的曲线,如图9所示。由图9可见,在弗劳德数Fr和压重块长度系数一定时,随着压重块布置间距的增加,管道最大冲刷深度呈现出递减的趋势。
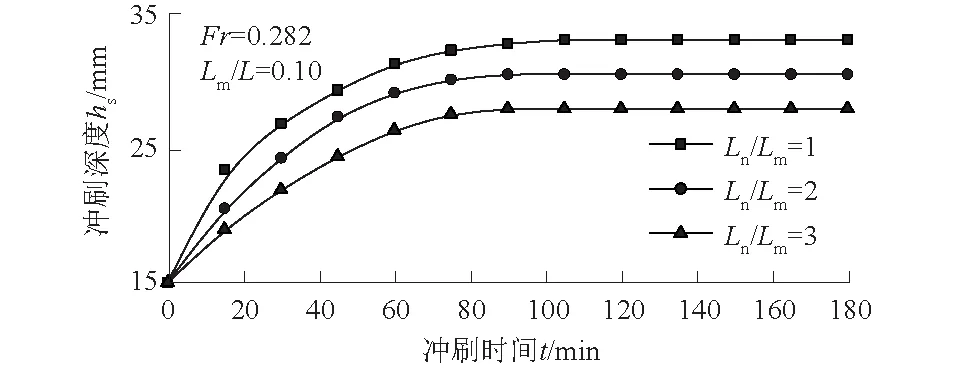
图9 不同压重块布置间距下管道冲刷深度变化曲线Fig.9 Curves of pipeline scouring depth under differentspacings between heavy blocks
3.3.2 压重块长度对管道冲刷的影响
弗劳德数Fr=0.282且压重块间距系数Ln/Lm=1时,管道附近河床达到冲刷平衡后的地形等高线如图10所示。随压重块长度系数增加,管道附近河床的整体冲刷深度呈现出递增趋势。压重块长度系数从0.1增加到0.2的过程中,未加压重块管道段的平均冲刷深度增加了20%,加压重块管道段的平均冲刷深度则增加了25%。经过对比发现,加压重块管道段的平均冲刷深度总是要比未加压重块管道段的平均冲刷深度高出20%~30%。压重块长度的增加会导致其对水流的阻挡作用加剧,从而使管道底部的局部冲刷流速进一步增大,管道冲刷深度也随之增加。
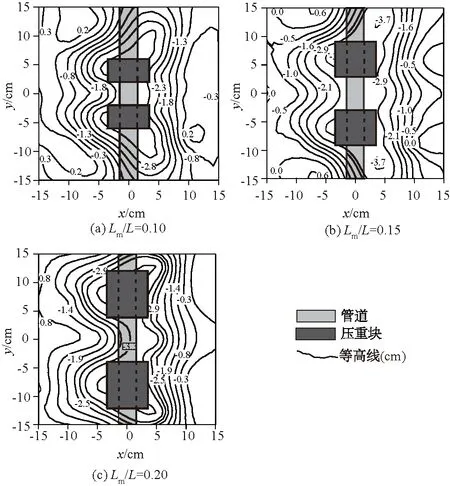
图10 压重块长度变化时冲刷地形Fig.10 Scouring terrian in the presence of varied heavyblock lengths
此外,在压重块长度系数从0.1增加到0.2的过程中,管道底部冲刷坑的中心点向河床下游方向移动了大约1.2倍管径D的长度。根据试验测得的地形数据可以绘制出不同压重块长度下管道冲刷深度随时间变化的曲线,如图11所示。由图11可知,在弗劳德数Fr和压重块间距系数一定的情况下,随着压重块长度的增加,管道最大冲刷深度呈现出递增的趋势。
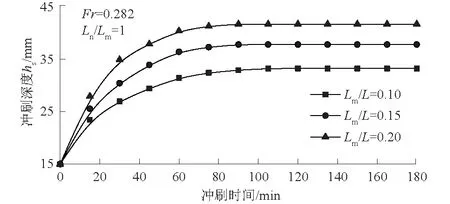
图11 不同压重块长度下管道冲刷深度变化曲线Fig.11 Curves of pipeline scouring depth underdifferent heavy block lengths
3.4 冲刷深度经验公式拟合与验证
试验中水下穿越管道附近河床冲刷是压重块、流体及河床三者共同作用的结果。因而穿越管道的局部冲刷直接受压重块参数、水动力条件和沙粒特性的影响。其中:水动力因素主要有流速v、水深h、重力加速度g;压重块参数有压重块长度系数Lm/L、压重块间距系数Ln/Lm;河床沙粒特性参数有中值粒径d50、泥沙重度γs等。用hm表示管道的最大冲刷深度,即
hm=f(v,h,g,Lm,Ln,L,d50,γs) 。
(2)
在一般条件下河床泥沙重度γs为常数,不作为变量考虑。因此式(2)可以化简为
hm=f(v,h,g,Lm,Ln,L,d50) 。
(3)
公式两边采用无量纲表示,即
(4)
基于以往管道冲刷深度的计算方法[23],并结合本文冲刷地形数据,对无量纲冲刷深度hm/d50与压重块长度系数Lm/L、压重块间距系数Ln/Lm和弗劳德数Fr的关系进行指数拟合,得
(5)
式(5)适用于Fr<1时砂质河床中穿越管道在压重块保护措施下的最大冲刷深度预测。由关系式可知,无量纲冲刷深度hm/d50与压重块长度系数Lm/L及弗劳德数Fr正相关,与压重块间距系数Ln/Lm负相关。为验证拟合式(5)的可靠性,图12列出了冲刷深度实测值与拟合公式计算值对比,可以看出,两者结果基本一致,说明经验式(5)对于预测裸露穿河管道在压重块保护措施下的最大冲刷深度具有较高准确性和可靠性。
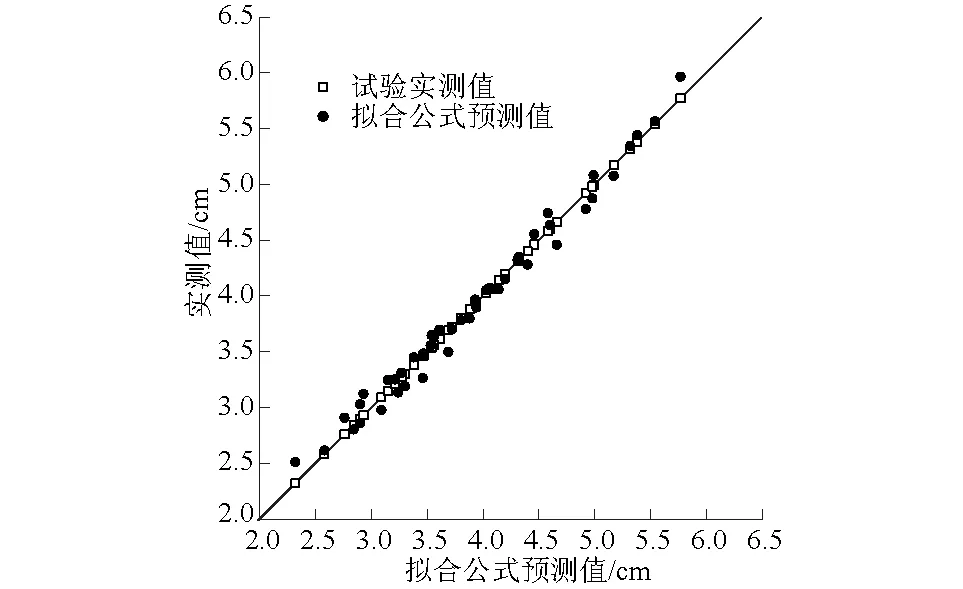
图12 管道最大冲刷深度实测值与计算值验证Fig.12 Comparison of maximum scouring depth betweenmeasured values and predicated values
4 结 论
通过开展水槽模型试验,研究了水下穿越管道在压重块保护措施下的冲刷特性,分析了压重块长度、压重块布置间距、水流流速、河道水深4种因素对管道周围河床冲刷地形和冲刷深度的影响,得出如下结论:
(1)水下穿越管道在压重块保护措施下的冲刷过程可以分为4个阶段,分别是冲刷坑形成、压重块迎流侧悬空、管道迎流侧悬空和冲刷平衡。
(2)管道的最大冲刷深度hm与流速v和压重块长度系数Lm/L正相关,与水深h和压重块间距系数Ln/Lm负相关。管道底部河床冲刷平衡历时则随冲刷流速v的增大而减小。
(3)采用量纲分析法得到无量纲冲刷深度hm/d50与压重块长度系数Lm/L、压重块间距系数Ln/Lm、弗劳德数Fr的函数关系式为hm/d50=339.9(Fr)0.79(Lm/L)0.32(Ln/Lm)-0.10,通过对比得到拟合公式预测值与试验实测值基本一致。
