不同铺设及联接型式的复合土工膜围堰应力变形特性

2022-04-16潘家军李浩民

长江科学院院报 2022年4期

徐晗，李波，潘家军，李浩民

(长江科学院水利部岩土力学与工程重点实验室，武汉 430010)

1 研究背景

复合土工膜是一种优良的防渗材料，具有防渗性能强、节约水泥与黏土用量、施工简捷等优点，已较为广泛地应用于国内外坝体防渗工程中[1-2]。同时，复合土工膜的相关研究亦取得了持续发展[3]。坝体防渗土工膜在透水性、渗漏量、稳定性及膜厚度等方面的研究与计算已有试验数据支持、定性的认识或准定量的公式可依[4]，土工膜应力变形模拟也有了一定的研究成果[5-6]，但对土工膜铺设及锚固型式方面的研究尚处于初始阶段。

复合土工膜常作为高土石围堰的防渗材料，可构成面膜或芯膜，跟随堰体变形而产生复杂的应力应变状态[7]。复合土工膜是一种柔性材料，具有一定的抗拉强度和伸长率，但在空间狭小且不均匀变形显著的地方如锚固处，由于夹具效应，依然容易产生应变集中而遭受破坏[8-10]。在拆除三峡工程二期围堰过程中就发现，复合土工膜在与混凝土防渗墙搭接处已发生了断裂[11]。要改善防渗土工膜的受力变形状态，避免产生过大的应变集中，需提高其与堰体的变形协调性。故改进复合土工膜在堰体中的铺设以及与刚性结构间的锚固型式，增强其对堰体变形的适应性，是复合土工膜作为防渗体系的土石围堰设计的关键。

李波等[12]曾分析了复合土工膜与下部防渗墙搭接处堰体填料与防渗墙的不均匀变形情况，提出了新的复合土工膜与下部防渗墙间的联接型式。刘军等[13]对预留伸缩节能够展开而发挥作用的力学条件进行了分析。目前针对围堰防渗土工膜铺设和锚固型式仅进行了少量研究，尚不充分。鉴于此，以离心模型试验为基础，采用新的土工膜三维有限元模拟方法进行数值模拟，研究围堰防渗复合土工膜不同铺设及联接型式下填筑期与蓄水期应力变形特性，为复合土工膜防渗工程的设计、施工和运行管理提供理论依据，对复合土工膜的实际工程应用具有重要的现实意义。

2 离心模型试验

参考某高土石围堰复合土工膜防渗心墙设计模型，开展复合土工膜的离心模型试验，研究填筑过程以及蓄水条件下复合土工膜的应变特性。

根据围堰原型，按模型比尺1∶100设计模型。模型箱尺寸为1.00 m(长)×0.40 m(宽)×0.80 m(高)。模型堰体总高44 cm，上游面坡度为1∶1.8，下游面坡度为1∶1.65，复合土工膜两侧分别采用5 cm厚的垫层。堰体填料选用原型场地粗砂，干密度为1.81 g/cm3；垫层料选用细砂，干密度为1.64 g/cm3。所用填料与原型围压填料缩尺后级配相似。复合土工膜模拟以抗拉强度、伸长率以及膜砂间界面摩擦系数满足相似条件为原则，近似选用抗拉强度为0.2 kN/m、伸长率为30%、与垫层料界面摩擦系数为0.29的织布代替土工膜，以避免放大土工膜的作用。由于模型箱尺寸限制无法模拟整个土石坝，仅模拟围堰重要的中下游部分。

为研究复合土工膜铺设型式及其与其他部位的联接型式对复合土工膜受力变形的影响，根据铺设及锚固型式开展3种不同的复合土工膜围堰离心模型试验方案，如表1所示。2种土工膜铺设型式见图1。

表1 复合土工膜围堰离心模型试验方案Table 1 Schemes of centrifugal model test for compositegeomembrane cofferdam

图1 复合土工膜铺设型式Fig.1 Laying pattern of composite geomembrane

采用激光位移传感器监测围堰表面沉降，微型孔压传感器监测水位上升，大量程应变片监测土工膜受力状态，监测布置见图2(a)所示，土工膜应变片布置见图2(b)所示。

图2 离心模型监测布置和复合土工膜应变片布置示意图Fig.2 Schematic diagram of centrifugal modelmonitoring and layout of compositegeomembrane strain gauge

模型装置好后，设定加速度目标值为100g(g为重力加速度)启动离心机。加速度增大至目标加速度并且变形相对稳定一段时间后，开始连续提升蓄水位至目标高度40 cm，通过各高程处微型孔压传感器反馈的孔隙水压力信息推算水位高度，对全过程堰体位移和土工膜应变进行实时监测记录。

图3为方案1坡顶及坡面各处测点沉降和水平位移随时间的变化曲线。分析表明：随着离心机加速度的逐渐增大，坡顶沉降以及坡面水平位移均逐渐增大；当加速度运行至100g时，沉降变形稳定；蓄水过程中坡顶沉降逐渐增大，坡面未产生较大水平位移。

图3 方案1坝体沉降(LDS1)和水平位移(LDS2,LDS3)随时间的变化Fig.3 Curves of settlement of monitoring point LDS1and horizontal displacement of monitoring points LDS2and LDS3 with time in scheme 1

图4为方案1土工膜各测点应变随时间的变化曲线。分析表明：随着加速度逐渐增大，土工膜各测点处应变均逐渐增大，当加速度运行稳定后应变逐渐稳定。蓄水后各测点处应变均有突变，断面中心线处应变逐渐增大(S1点)，而靠近侧边的应变逐渐减小(S3点)。

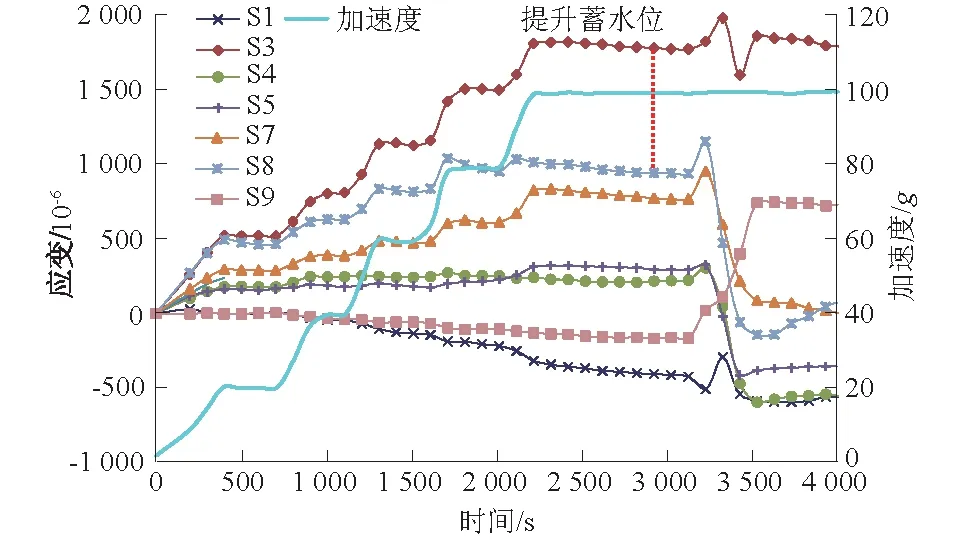
图4 方案1土工膜应变随时间的变化曲线Fig.4 Curves of geomembrane strain with time inscheme 1

各方案离心模型试验监控最大值见表2。离心试验结果表明：采用复合土工膜进行围堰防渗设计时，在水压力的作用下容易在复合土工膜与底部防渗墙及两侧山体搭接部位产生应力集中，最大拉应变出现在复合土工膜与两侧山体搭接的上部(S3点)，而可伸缩柔性搭接可以改善水压力导致的土工膜局部拉应力增大，最大拉应变出现在模型底部两侧(S9点)。

表2 离心模型试验监控最大值Table 2 Maximum monitored values in centrifugalmodel test

3 数值模拟方法及参数

离心模型试验只能得到复合土工膜局部点的应变空间分布状态，无法获知联接处的应力变形。因此，在离心模型试验的基础上开展数值模拟研究，建立跟实际模型尺寸相符的三维有限元模型。

土工膜三维有限元数值模拟研究甚少，目前主要采用的方法有3种：将土工膜嵌入实体单元、为土工膜建立实体单元并设置接触面单元以及不建立土工膜单元而将其视为依附于其他单元表面[14]。

以上方法各有不足。本项目采用ABAQUS软件提供的薄膜单元M3D4来模拟复合土工膜。薄膜单元属柔性抗拉材料，不具备抗压和抗弯特性，较好地反映了土工膜自身的基本力学特性。在复合土工膜与上、下游垫层料之间均设置了接触。接触面的力学模型可分为法向模型和切向模型，能较好地模拟土工膜与垫层料之间的张拉脱开、剪切滑移等接触力学特性。同时在此方法中，水压力也直接加在土工膜上，可真实有效地模拟土工膜的应力应变。

根据试验测试，离心模型试验选用堰体土料Duncan-Chang模型参数如表3所示，其中ρd为干密度，c为黏聚力，φ为内摩擦角，Rf为破坏比，K、n为切线弹性模量的试验常数；G、F、D均为切线泊松比的试验常数；土工膜与堰体垫层料间界面摩擦系数为0.29，复合土工膜弹性模量取100 MPa。

表3 Duncan-Chang模型(E-μ)参数Table 3 Parameters of Duncan-Chang model (E-μ)

离心模型试验过程的数值模拟步骤如下：

(1)赋予土体初始应力构建初始模量。

(2)考虑土体与模型箱之间的摩擦作用，静态地模拟20g、40g、60g、80g、100g加速度作用下的位移应力场。

(3)在竣工期100g加速度计算结果的基础上施加相应水压力与浮力，再次计算在100g加速度作用下的位移应力场。

4 数值模拟结果分析

图5为方案1，即平直铺设土工膜并采用锚固联接型式时，围堰与土工膜在蓄水期的变形计算成果等值线。数值计算显示蓄水期堰体最大沉降为7.4 mm；土工膜存在局部应变集中部位，锚固部位最大主拉应变为2.5%，发生在土工膜顶端与模型箱锚固处。

图5 方案1蓄水期围堰沉降等值线和土工膜变形等值线Fig.5 Contours of cofferdam settlement and geomembranedeformation in scheme 1 in water-storage period

若更换为S型铺设土工膜，即方案2，计算结果如图6所示。分析可知，蓄水期坝顶最大沉降3.9 mm，几乎减小到方案1沉降值的一半；土工膜与模型箱周边约束处最大主拉应变为2.0%，分布在土工膜顶端与模型箱锚固处。将图6与图5相比，可知S型铺设方案2的整个区域土工膜应变均大幅小于直线型铺设方案1的土工膜应变，表明S型铺设土工膜受力更合理。

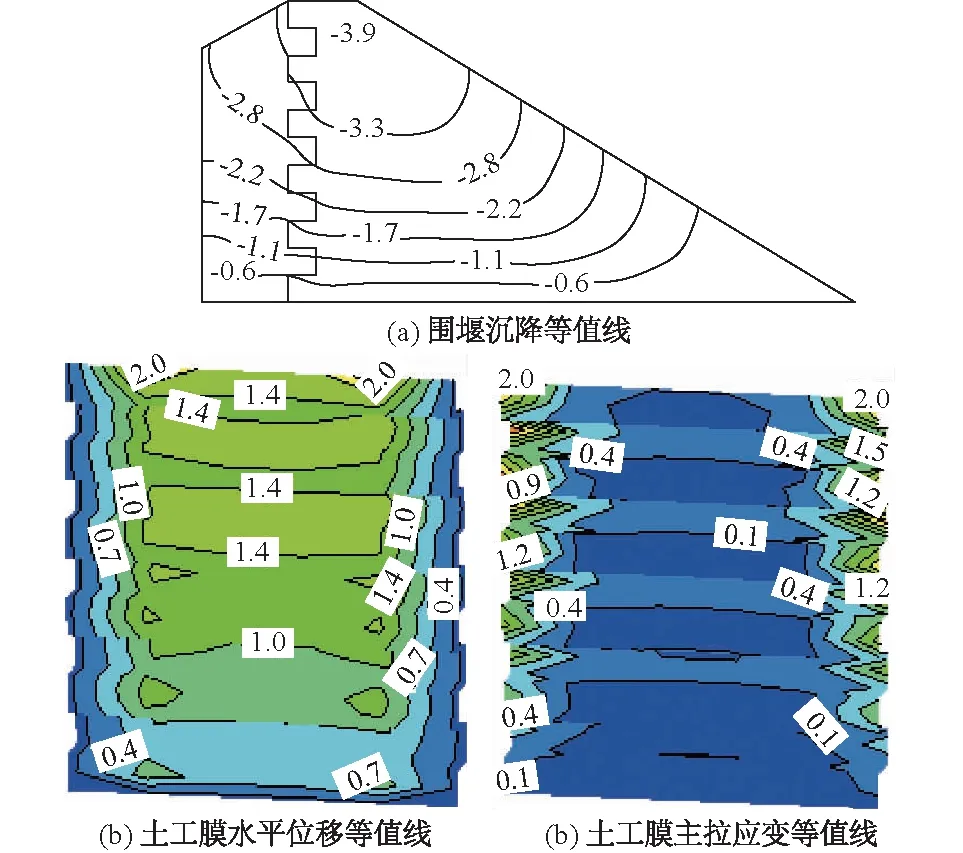
图6 方案2蓄水期围堰沉降等值线和土工膜变形等值线Fig.6 Contours of cofferdam settlement and geomembranedeformation in scheme 2 in water-storage period

方案3与方案2的区别在于土工膜侧边采用可伸缩柔性联接。图7为方案3围堰与土工膜的计算成果等值线。可知蓄水期最大沉降5.9 mm；土工膜最大主拉应变为0.3%，与采用锚固联接的方案2相比，方案3土工膜两端与中部应变基本呈现分布均匀状态，没有明显的应变集中区域，这是由于土工膜与模型箱周边柔性约束所致。

图7 方案3蓄水期围堰沉降等值线和土工膜变形等值线Fig.7 Contours of cofferdam settlement and geomembranedeformation in scheme 3 in water-storage period

为验证土工膜模拟算法的准确性，将有限元计算成果与离心模型试验结果进行对比。离心模型试验中应变片的测试结果是土工膜水平方向的应变值。将试验中出现最大应变值监控点处的土工膜水平应变与相应位置的土工膜水平应变计算值对比，如表4所示。由图4可知模型的沉降与土工膜的拉应变均吻合较好，由此可认为本文所采用的土工膜算法及土体本构模型具有一定的可靠性。