滚石运动特性的物理模型试验研究

刘彦辉

摘要： 滚石的运动特征研究是滚石灾害防治的重要前提，而坡表覆盖层和滚石自身特性是影响其运动特征的重要因素。以斜坡覆盖层材质为变量，开展物理模型试验，研究了混凝土坡面和土质坡面下滚石试块的运动特征;并在此基础上，以在建合壁津高速公路边坡为例，开展滚石运动特征数值模拟研究，以运动速度、转动速度、运动能量等为指标分析了滚石形状和尺寸对其运动过程的影响。结果表明：形状和尺寸对滚石运动特征影响较大，滚石越接近球形、尺寸越小，其运动速度越大、转动速度越大;滚石在下落过程中有30%以上的势能通过坡面碰撞损耗，在滚石防治工程中应考虑这部分损耗，而滚石转动能量只占总动能的1/30～1/10，因此一般不单独考虑滚石的转动过程。研究成果可为滚石防治工程的设计及优化提供参考。

关 键 词： 滚石运动特征; 物理试验; 离散元模拟; 合壁津高速公路

中图法分类号：  P642.2

文献标志码：  A

DOI： 10.16232/j.cnki.1001-4179.2022.03.030

0 引 言

滚石运动过程是滚石灾害防治工程中的关注重点，其基本形式可划分为滚动、斜抛和碰撞  [1-2] 。国内外学者对斜坡滚石运动特征规律开展了广泛的研究：黄润秋等  [3] 通过开展滚石现场原位试验研究了坡角对滚石运动特征的影响;Niklaus等  [4] 通过将自研的“StoneNode”仪器植入滚石内部获取了滚石运动特征参数，并对其运动规律进行了分析;Giacomini等  [5] 将“立体测量影像系统”应用于滚石运动轨迹分析中，通过重建的滚石三维运动轨迹实时判断滚石的运动情况;张龙等  [6] 开展室外滚石运动试验得出试块形状是影响滚石运动的最显著因素;Spadari  [7] 通过原位试验得到滚石恢复系数的经验值;杨仲元  [8] 采用数值分析手段对滚石运动恢复系数进行了讨论，并提出基于衰减反弹接触法（DROM）的滚石路径分析方法;Liang，Clement等  [9-11] 收集了滚石运动过程中的震动信号，并通过震动信号反演得到滚石运动特征规律。此外，还有部分学者采用数值模拟手段研究了影响滚石运动过程的因素  [12-13] 。

本文依托在建合壁津高速公路危岩落石防治工程项目，采用“室内试验+数值分析”的手段，对滚石运动特征进行了系统性研究，研究成果可为该区段滚石防治工程的设计提供设计参考。

1 研究区概况

研究区域地处四川盆地东侧，大巴山前侧，地貌类型为山地地貌，由构造剥蚀作用形成。区域内地势东南高西北低，存在较大落差，最高点在南侧山脊高程约 820 m，最低点在北部沟谷地带高程约480 m，相对高差约340 m（见图1）。

研究区危岩落石体量和方量较大，体积从几方至上千方不等，且多散布于边坡上，因坡表植被和坡度影响产生堆积。区域内危岩落石主要为中风化砂岩，且多为带菱角的不规则形状，块径为2～50 cm不等，并伴有少量块径为80～250 cm的大块石出现。落石體积集中于0.125～4.0 m  3 之间，最大尺寸可达15 m  3 。

2 物理模型试验

2.1 试验设计

物理模型试验结合研究区背景进行相似比的考虑。通过运用相似第二定理，将应力 σ、应变ε、泊松比μ、弹性模量E、位移δ、接触力F作为量纲分析参量，并选取E、δ 为基本量。

f σ，ε，μ，E，δ，v，J =0 （1）

各参数量纲可为

σ =ML  -1 T  -1   E =ML  -1 T  -1   δ =L  F =MLT  -1   （2）

由此可得到量纲关系式为

π 1= σ E  y 1 δ  y 2  = ML  -1 T  -1    ML  -1 T  -1     y 1 L  y 2   π 2= ε E  y 3 δ  y 4  = ε   ML  -1 T  -1     y 3 L  y 4   π 3= μ E  y 5 δ  y 6  = μ   ML  -1 T  -1     y 5 L  y 6   π 4= F E  y 7 δ  y 8  = MLT  -1    ML  -1 T  -1     y 7 L  y 8    （3）

计算各式π值为

π 1= σ E ，π 2=ε，π 3=μ，π 4= F E 1δ 2  ，

因而试验所采用的相似准则为

C ε=C μ=1 （4）

式中： C ε为应变相似比，C μ 为泊松比相似比。

试验以几何相似比 C L =100为基础，对其他相似比参数进行合理控制，使物理模型试验能与现场情况较好拟合。根据研究区斜坡坡度范围构建物理模型试验，如图2所示，坡面形态与研究区基本保持一致，如图3所示。

根据图3可知，试验斜坡模型高1.0 m，长0.9 m，坡度变化范围介于26°～70°之间，分别选用混凝土和黏土作为坡表覆盖层，用来模拟边坡表面为裸露岩体和土体的2种工况。试块形状考虑对运动最有利的方形试块，试块尺寸为3 cm×3 cm×3 cm，在物理性质上，试块制作采用C30混凝土且泊松比为0.3，这与现场调查得到的砂岩物理性质存在相似性。

采用如图4所示的方法释放试块，将试块置于坡顶，向临空面缓缓推到，靠其自身重力下落。运动全过程由摄像机侧面拍摄，记录停止位置、运动距离及偏移量。为消除试验误差，每组试验重复进行60次，并选取90%的可用组数开展后续结果计算。

2.2 试验理论计算

2.2.1 试块运动速度

假设滚石发生运动后，于 t  a 时刻运动到A点（x  a ，y  a ），于t  b 时刻运动到B点（x  b ，y  b ） （见图5），由此可计算滚石竖向和横向偏移速度：

v x= x b-x a t b-t a ，v y= y b-y a t b-t a  （5）

2.2.2 试块恢复系数

根据块体非弹性碰撞相关理论，滚石在运动过程中常与坡面产生碰撞耗能作用，导致其运动速度下降，速度减幅即为能量损耗的大小，计算公式为

R= u r u i  （6）

式中： R为滚石恢复系数，u  i 和u  r  分别为滚石碰撞坡面前后的运动平均速度（见图6）。

由于滚石在斜坡上的运动可分解为切向和法向，因此分别采用法向恢复系数和切向恢复系数表征滚石的速度变化情况：

R n= u  r，n  u  i，n   （7）

R t= u  r，t  u  i，t   （8）

2.3 试验现象描述

根据对试验现象的观察，试块下落过程可划分为快速下落阶段和缓速下落阶段（见图7）。

（1） 快速下落阶段。该段为运动的前半程，斜坡坡角较大，试块以滚动和跳跃为主要姿态，试块碰撞耗能较低，速度在较短时间内快速增长。

（2） 缓速下落阶段。由于斜坡坡角逐渐减小，该段试块运动模式以滚动为主，试块与坡面碰撞次数增多，试块运动增速明显减缓。

2.4 试验结果分析

2.4.1 土体覆盖层对运动速度的影响

图8为土体有无覆盖层情况下对所有试验组求均值后得到的速度时程曲线。试块从坡顶开始下落后速度迅速增大，并且在这个过程中，试块不断旋转、与坡体产生碰撞，曲线上每一个速度的突变点都表示碰撞点。

有土体覆盖层工况下，试块于0.7 s运动至坡底，运动速度峰值为2.7 m/s;无土体覆盖层工况下，试块于0.8 s运动至坡底，运动峰值速度为2.1 m/s。试块在到达坡底后，由于碰撞耗能作用，以及试块在平地发生的滚动摩擦耗能，速度进一步减小趋于零。

对曲线进一步分析可得到，土体覆盖层的有无对滚石运动速度存在较大影响，以峰值运动速度为例，两种工况差值接近于20%，试块与坡面发生碰撞后速度的变化也十分明显。

2.4.2  土体覆盖层对运动距离与偏移量的影响

图9为滚石试块运动距离-偏移量示意图。根据试验数据绘制有无覆盖层条件下横向偏移量和水平运动距离的散点图如图10所示。由图10可知：试块偏移量与运动距离存在强相关关系，且在多数场景下，横向偏移量与水平运动距离成正相关关系，且散点大多位于 d =0.42l-46.3和 d =0.23l-19.7两条曲线之间的区域。

两种工况下，试块的水平运动距离多集中在160～200 cm间，分别达到有土体覆盖层工况和无土体覆盖层工况试验组数的75%和83%以上。但2种工况下，试块不同水平运动距离区间存在显著差异，在有土体覆盖层工况下，试块主要停留在160～180 cm之间，达到25次，占比约50%，而在无覆盖层工况下，有17次试验试块停积在这个距离内，占比约30%;在180～200 cm区间，多停积无覆盖层工况试块，记数为28次，超过总数的50%，无覆盖层情况下在该区间停积试块占比为30%，与水平运动距离相比，试块横向偏移也呈现出相似规律。据此可知，在无土体覆盖层情况下，试块表现出更强的运动特性。

此外，采用偏移比表征滚石横向运动的能力：

α= d l  （9）

式中： l 为滚石沿最大坡降方向的运动距离， d 为滚石横向偏移量。

图11为试块水平运动距离与偏移比的关系散点图。从图11可以看出：试块偏移比分布于0.08～ 0.18 的区间内，超过90%的数据分布于偏移比为0.12～0.16的区间内。此外，无土体覆盖层的试验组具有较高偏移比（>0.14）的组数更多，约为69%，说明无土体覆盖层情况下滚石具有较强的运动能力。

2.4.3 有无覆盖层对运动恢复系数的影响

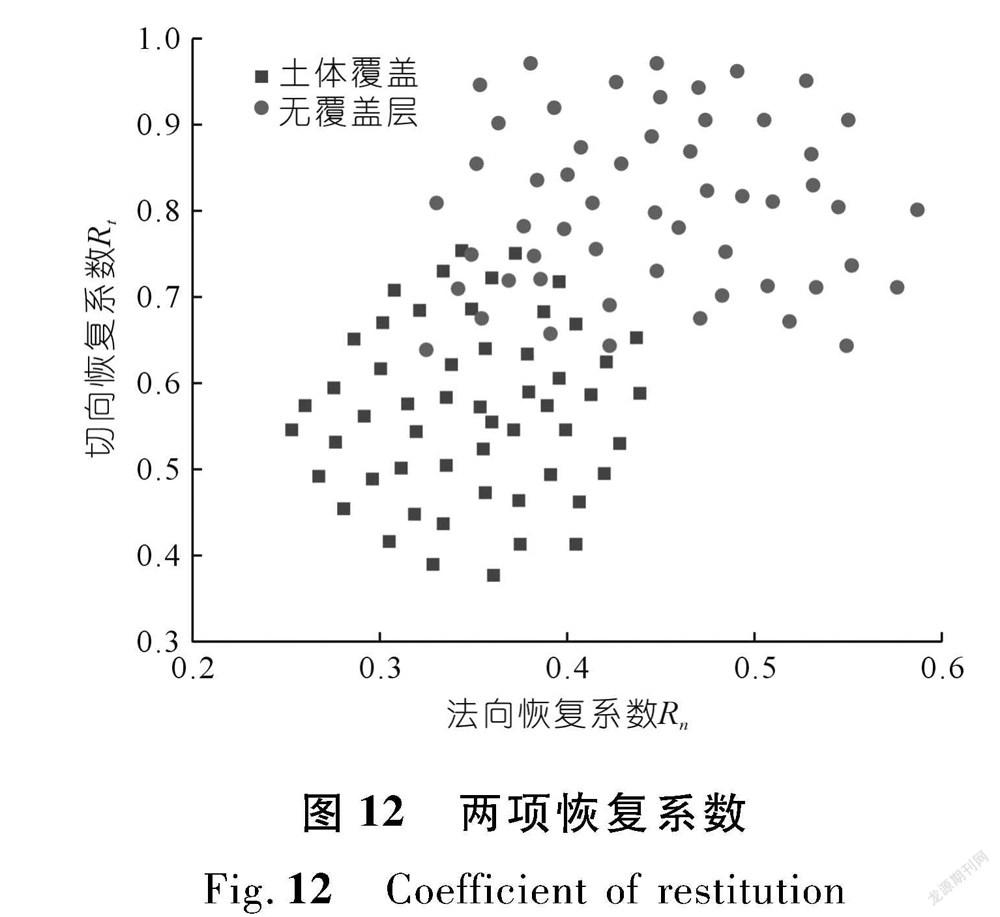
通过对每组试验切向与法向恢复系数的典型值进行计算，绘制有无土体覆盖层情况下恢復系数的关系如图12所示。由图12可知：不同覆盖层条件下2项恢复系数有较大区别，对于有土体覆盖层工况，法向恢复系数位于区间0.25～0.45，切向恢复系数位于区间0.36～0.75;对于无土体覆盖层工况，法向恢复系数位于区间0.35～0.58，切向恢复系数位于区间0.63～ 0.96 。后一种工况下的恢复系数明显大于前者，这与Asteriou文中岩质边坡恢复系数明显大于土质边坡的结论类似。此外，无论哪种工况，恢复系数值分布较散乱，这可能与滚石与坡面碰撞时的姿态有关，有的是碰撞点，有的是碰撞面，另外由于试验组数有限，统计数据较少，也会出现这种情况。

3 滚石运动过程数值模拟研究

为弥补物理实验组数较少造成的结果局限性，使结果更为真实可靠，因此采用基于离散元方法的PFC软件选取研究区内边坡研究滚石的运动过程。

3.1 计算模型校正

以室内试验为蓝本，1 ∶1构建离散元模型，模型由运动坡面和停积平台两大部分组成，坡体尺寸如图13所示。参照室内试验将坡体分为7段，停积平台根据需要取1.0～1.5 m。

模拟过程中，不考虑滚石的变形和破裂，不考虑坡体表面的形变，采用线性接触模型，离散元参数取值参考蒋景彩等  [14] 所提出的滚石离散元数值模拟参数标定方法进行标定，计算取值如表1所列。

图14为土质覆盖层和混凝土覆盖层2种工况下的物理模型试验与数值计算速度趋势对比分析图。由图14可知：数值计算结果一定程度上还原了物理模型试验，绝大部分数据点的速度误差值控制在13%以内，因此可认为该离散元的模拟分析方法和所选取的计算参数适宜，可用于滚石运动过程的分析。

3.2 模拟计算工况

选取拟定研究区边坡为研究对象，在此基础上开展数值计算工作，以拟定研究区1 ∶500地形图为参照构建1 ∶1边坡三维计算模型。对所选边坡开展野外调查，将滚石大致划分为“条状”和“块状”，并结合调查结果加入较不利的“似球状”滚石，每种形状的试块分别采用50，100，150 cm 3种尺寸。采用clump软件生成滿足要求的试块模型（见图15）。所选定的斜坡坡度较缓、坡表覆盖层主要为强风化砂岩、松软土体，可参照表1中土质坡面的离散元参数取值。

3.3 计算结果分析

（1） 运动速度。图16为条状、块状、似球状滚石的运动速度时程曲线。从图16可以看出：各块径下滚石试块释放后其速度迅速的增大，后迅速减小至零。小尺寸滚石峰值运动速度往往最大。条状、块状和似球状小尺寸滚石运动速度分别为13.7，13.8 m/s和17.8 m/s，最大块径的峰值速度分别为8.2，8.6 m/s和11.3 m/s，这可能是受惯性影响，较小质量滚石易改变运动状态，更容易获得较大速度。此外，形状对速度也有影响，越是接近球形，滚石运动速度越大;同尺寸的滚石，似球状峰值速度分别比条状和块状滚石速度大约20%～37%。

（2） 转动速度。滚石在下落过程中转动和平动交替或同时存在。图17为不同形状下滚石转动速度模拟曲线图。对于条状、块状、似球状块径50 cm的滚石，其峰值转动速度分别为50，55 rad/s和58 rad/s;而对于块径250 cm的不同形状滚石，其峰值转动速度仅为5.2，6.3 rad/s和7.1 rad/s，具有显著的差异。这也表明对于下落的滚石，其质量较大时速度的变化多由平动速度影响，而质量较小时转动速度对合速度的影响很大。似球状滚石转动速度-时间曲线不同于其他两种工况，其曲线较平滑，无明显或很少存在“阶梯”，表明这种形状更易发生运动状态，特别是转动速度的变化，稳定性较差。

（3）  能量变化。滚石下落过程中，随着运动速度的变化，能量也随之改变。图18为不同形状、不同块径滚石运动过程中机械能的变化。运动初始阶段，滚石的全部机械能为重力势能，随着沿斜坡向下运动，势能转化为动能，后者根据其运动形式又可分为平动动能和转动动能。转动动能在总动能中只占极小一部分约1/30～1/10。因此在滚石防治设计中往往忽略这部分能量。

（4） 运动轨迹。图19表示了不同形状滚石运动轨迹图，其中 条状、块状滚石受其形状因素影响明显，

呈现出不同的运动轨迹，运动距离也存在较大的偏差。而不同块径似球状滚石的斜坡运动轨迹相似，但到达坡底时，大尺寸滚石因接触面积大会受到更大的阻力，而小尺寸滚石受阻力较小，因而运动距离较远。表2统计了不同形状滚石运动过程参数，在仅考虑运动速度、转动速度、运动距离情况下，小尺寸滚石运动能力、活动性更强。

4 结 论

为探究坡表覆盖层及滚石自身特性对滚石运动特征的影响，本文采用室内试验及离散元模拟的方法，系统研究了坡表不同覆盖层和滚石块径、形状对滚石运动特性的影响，结论如下。

（1） 坡表覆盖层性质对滚石运动速度有显著影响，混凝土坡面较土质坡面滚石运动速度提高约20%。下落过程中，斜坡坡度对速度的变化影响较大，较陡时（试验条件下大于40°）滚石呈现出显著加速状态，小于这个角度则加速度明显减小。

（2） 滚石运动距离与其运动速度有较好的相关性，大多数情况下，混凝土坡面滚石的运动距离更大，平均比土质坡面大约20 cm，同时其横向偏移量也更大约是另一种工况下的1.2倍。试验中，约90%滚石的运动偏移比在0.08～0.16区间，同时近70%的混凝土坡面运动试块的偏移比大于土质坡面，表明在混凝土坡面上的滚石具有较强的运动能力。

（3） 对边坡滚石运动的数值模拟表明，滚石运动速度受形状和块径影响，相同块径下滚石越接近球形，其运动速度越快，模拟中似球状滚石可比同块径下的条状滚石运动速度大约30%;相同形状下的滚石，较小质量的可比大质量速度大近60%。

（4） 滚石下落运动过程中，运动状态包括平动和转动，和速度有类似的趋势，小质量滚石由于惯性小，易改变运动状态，其在运动过程中转动速度往往较大，相反，大质量滚石一般具有较小的转动速度，但这种变化与滚石形状关系不大。

（5） 滚石下落过程中涉及复杂的能量转化，重力势能转化为动能和与坡面碰撞损耗的内能，动能则包括平动动能和转动动能，后者一般是前者的1/10～ 1/30 ，因此在滚石灾害防治过程中，通常不考虑转动能量的影响。

（6） 综上所述，在实际工程中，可根据本文研究得到的不同覆盖层性质、坡面类型、滚石形状和块径对滚石的运动距离、运动速度、偏移比的影响，为滚石防治结构的安置位置、修筑高度和能级等提供合理化建议。

参考文献：

[1]  胡厚田.崩塌与落石[M].北京：中国铁道出版社，1989：1-19.

[2] 赵丽娜，周科平，高峰，等.露天矿边坡滚石运动特征及控制[J].灾害学，2008（3）：76-79.

[3] 黄润秋，刘卫华，周江平，等.滚石运动特征试验研究[J].岩土工程学报，2007（9）：1296-1302.

[4] NIKLAUS P，BIRCHLERT，AEBI T，ET A L.StoneNode：a low-power sensor device for induced rockfall experiments[C]∥2017 IEEE Sensors Applications Symposium（SAS）.IEEE，2017.

[5] GIACOMINI A，THOENI K，LAMBERT C，et al.Experimental study on rockfall drapery systems for open pit highwalls[J].International Journal of Rock Mechanics & Mining ences，2017（56）：171-181.

[6] 张龙，雍睿，倪卫达.滚石运动特征影响因素分析[J].安全与环境工程，2011，18（3）：17-21.

[7] SPADARI M，GIACOMINI A，BUZZI O，et al.In situ rockfall testing in New South Wales，Australia[J].International Journal of Rock Mechanics & Mining Sciences，2012，49（2）：84-93.

[8] 杨仲元.道路边坡危岩落石运动路径研究[J].公路交通科技，2010，27（1）：34-38.

[9] LIANG F，VERONICA P，EMANUELE I，et al.Rockfall seismic features analysis based on in situ tests：frequency，amplitude，and duration[J].Journal of Mountain Science，2019，16（5）：955-970.

[10]  CLMENT H，ANNE MA，GILLES G，et al.Spatio-temporal evolution of rockfall activity from 2007 to 2011 at the Piton de la Fournaise volcano inferred from seismic data[J].Journal of Volcanology and Geothermal Research，2017，333-334：36-52.

[11] CLMENT H，JEAN-PHILIPPE M，FRANCK Br，et al.Single-block rockfall dynamics inferred from seismic signal analysis，2017（5）：283-292.

[12] LEINE R I，SCHWEIZER A，CHRISTEN M，et al.Simulation of rockfall trajectories with consideration[J].Multibody Syst Dyn，2014，32：241-271.

[13] HU J，LI S，LI L P，et al.Field，experimental，and numerical investigation of a rockfall above a tunnel portal in southwestern China[J].Bull Eng Geol Environ，2017，77：1365-1382.

[14] 蔣景彩，能野一美，山上拓男.滚石离散元数值模拟的参数反演（英文）[J].岩石力学与岩土工程学报，2008，27（12）：2418-2430.

（编辑：刘 媛）

Physical modelling experiment on rockfall motion characteristics

LIU Yanhui

（ China Railway First Survey and Design Institute Group Co.，Ltd.，Xian 710043，China ）

Abstract：

The research on the motion characteristics of rockfall is an essential vital premise to preventing and controlling the disaster of rockfall.Furthermore，both the covering layer of the slope surface and the rockfall characteristics are essential factors that affect the motion characteristics.Taking the material of the slope covering layer as a variable，a physical test was conducted to study the motion characteristics of rockfall on the concrete slope and soil slope.On this basis，taking the slope of the Hechuan-Bishan-Jiangjin Expressway as an example，the numerical simulation study of the motion characteristics of rockfall was carried out.The influence of the shape and size of the rockfall on the movement process was analyzed by considering the velocity，rotation velocity，and kinetic energy as indicators.The results showed that the shape and size significantly influence the motion characteristics of the rockfall.The closer to a ball-likely shape and the smaller size，the greater the movement speed and rotation speed.More than 30% of the potential energy of the rockfall was lost during the collision，which should be considered in the rockfall stone control project.The rotational kinetic energy of the rockfall only accounted for 130～110 of the total kinetic energy，so the rotating process of rockfall was generally not considered separately.The research results can provide reference for the design and optimization of the rockfall prevention project.

Key words：

rockfall motion characteristics;physical modelling experiment;discrete element simulation;Hechuan-Bishan-Jiangjin Expressway