基于直线积分边界元法的温度应力研究

刘彪 高宇 李通盛 程勇刚 王桥 周伟

摘要： 边界元法作为一种半解析解的数值计算方法，除了在同自由度下能够获得相对更高的精度以外，更为突出的优点是降维，只需要对研究域的边界进行离散。但是在进行温度应力问题求解时，积分方程中会出现域积分。为了保证边界元法降维的优点，基于散度定理提出将直线积分法的域积分转化为边界积分。边界积分可以用带积分点的边界单元来计算。每个积分点可以构造一条积分线，由积分线上的线积分计算域积分。同时为了获得更高的精度，可以利用背景单元网格将积分线切割成更多的子线进行计算。最后通过一个矩形梁的热弹性分析和一个重力坝的温度应力分析验证了所提方法的有效性和精度。

关 键 词： 直线积分边界元法; 降维; 域积分; 热应力

中图法分类号：  TV311

文献标志码：  A

DOI： 10.16232/j.cnki.1001-4179.2022.03.027

   0 引 言

對于混凝土结构而言，无论是施工期还是运行期，温度应力自始至终是一个关键的影响因素  [1-4] ，如若处理不当，极有可能产生温度裂缝，进而影响大坝结构安全，因此进行混凝土坝内部的温度应力模拟分析是极为必要的。当前，有限元法（FEM）是一种广泛应用的数值方法，也是进行坝体力学分析的主流计算手段。而相较于有限元法，边界元法具有模型重建容易、只需要对边界进行离散化计算等优点  [5-8] 。

但是当考虑温度应力时，在边界方程中会出现域积分，进而使得边界元法失去了只需离散计算边界的优点。为此，许多学者开展了研究。最为直接的方法是利用直接域积分法  [9] ，直接对研究域进行单元划分，但是边界元法因此失去了只要对边界进行离散计算的优点。因而找出能保留边界元法优点的计算方法成为了研究的重点。比如双互易法（Dual Reciprocity Method，DRM）  [10-12] ：在DRM中，非齐次项可以用一系列函数进行逼近拟合，比如径向基函数（Radial Basic Function，RBF），然后利用第二互易将域积分转换为边界积分，只需要边界上和域内点的信息即可进行计算。但是该方法的精度较大程度上取决于域内点的位置和分布以及用来拟合逼近非齐次项的函数的种类。另外还有多互易法（Multiple Reciprocity Method，MRM）  [13] ，该方法多次应用互易定理到一系列高阶基本解上，进而将域积分转化为边界积分。除此之外，特殊解法（Particular Solution Method，PSM）也是一种有效的计算方法，通过构造特殊解来拟合逼近。此外，高效伟教授提出了一种新的计算方法：径向积分法（Radial Integration Method，RIM），该方法可以对径向积分法中的径向积分进行直接计算或者和径向基函数耦合进行计算。

本文采用了一种新的直线积分法（Line Integration Method，LIM）处理域积分  [14-15] 。直线积分法基于散度定理将域积分转化为包含一维线积分的边界积分，只需要对边界进行离散，首先通过边界单元和八叉树构建积分线，然后对一维积分线的结果进行求和即可得到最终结果。

1 考虑温度应力的边界积分方程结合前人研究，可知控制方程为

λ+μ u  j，ji +μu  i，jj - λ 1+v  ν βθ  ，i   y  =0 i，j=1，2; y ∈ Ω   （1）

式中：Ω为研究域，其边界为Γ; μ和λ为拉梅常数;ν代表泊松比;θ代表温度场;β 为热膨胀系数。

1.1 位移积分方程

结合贝蒂互易定理，通过推导可以得到正则化的位移积分方程  [16] ：

c  ij   x  u i  x  = ∫  Γ U  ij   x ， y  t j  y   d  Γ   y  -  

∫  Γ T  ij   x ， y  u j  y   d  Γ   y  -

∫  Ω U  ij，j   x ， y   λ 1+v  v βθ  y   d  Ω   y   （2）

式中： U  ij   x ， y  和T  ij   x ， y   为开尔文基本解，具体表达为

U  ij   x ， y  = 1 2A 1μr  h-1   A 2δ  ij   h-2  ln   1 r  +h-1 +r  ，i r  ，j   T  ij   x ， y  = -1 A 1r h {r  ，k n k[A 3δ  ij +3r  ，i r  ，j ]-A 3 r  ，i n j-r  ，j n i     （3）

以及

A 1=4 π h 1-ν  A 2=3-4ν A 3=1-2ν i，j=1，2 h=1   （4）

式中：  x = x  x 1，x 2 和 y=y y 1，y 2 分別为源点和场点;r 为2点之间的距离。

r  ，i =  r  x i  （5）

式（5）代表 r对x i 求导得到的导数，以及kronecker符号 δ  ij  为

δ  ij =  1，i=j 0，i≠j   （6）

此外，

U  ij，j   x ， y  =   -1    h+1 A 3r  ，i  A 1μr h  （7）

式（2）可以整理为以下形式：

c  ij   x  u i  x  =∫  Γ U  ij   x ， y  t j  y   d  Γ   y  -

∫  Γ T  ij   x ， y  u j  y   d  Γ   y  -∫  Ω  Φ  i  x ， y  βθ  y   d  Ω   y   （8）

其中，

c  ij   x  =   1 2 δ  ij ，边界点 δ  ij ， 域内点    （9）

Φ  i  x ， y  = -2 1+ν r  ，i  A 1r h  （10）

显而易见，式（8）中出现了一个域积分：

D 1=∫  Ω Φ i  x ， y  βθ  y   d  Ω   y    （11）

1.2 内部应力积分方程

结合高效伟教授编著的《高等边界元法》，可得内部应力积分方程：

σ  ij   x  =βθ  y  ∫  Γ r  ，m n m ln  r r  Ψ   ij   x ， y   d  Γ   y  +

∫  Ω βθ  y   Ψ   ij   x ， y   d  Ω   y  -∫  Ω βθ  y   Ψ   ij   x ， y   d  Ω   y  +

∫  Γ U  ijk   x ， y  t k  y   d  Γ -∫  Γ  Τ   ijk   x ， y  u k  y   d  Γ -δ  ij bβθ  y   （12）

其中，

Ψ   ij   x ， y  = -4μ 1+ν  δ  ij - h+1 r  ，i r  ，j   A 1r  h+1   （13）

b= μ h+2  1+ν  3 1-ν   （14）

U  ijk   x ， y  =  1 A 1r h  A 3 δ  ki r  ，j +δ  kj r  ，i -δ  ij r  ，k  +     h+1 r  ，i r  ，j r  ，k   （15）

T  ijk   x ， y  = 2μ A 1r  h+1    h+1 r  ，m n m A 3δ  ij r  ，k +    v δ  ik r  ，j -δ  jk r  ，i  - h+3 r  ，i r  ，j r  ，k  + A 3  h+1 n kr  ，i r  ，j +n jδ  ik +n iδ  jk  + ν h+1  n ir  ，j r  ，k +n jr  ，i r  ，k  -  A 2-2 n kδ  ij   （16）

而当 x ∈Γ时，边界面力方程为

c  ij   x    t   j  x  =c  ij   x  σ  ij   x  n j  x   （17）

同样可以观察出，式（12）中出现两项域积分

D 2=∫  Ω βθ  y   Ψ   ij   x ， y   d  Ω   y   （18）

D 3=∫  Ω βθ  x   Ψ   ij   x ， y   d  Ω   y   （19）

2 直线积分边界元法

2.1 基础理论

本节首先介绍退到直线积分法的一些基本定理，详细的论证过程参见文献[15]。

理论1：假设研究域  Ω 为一个有界平面区域，具有 Lipschitz 边界 Γ 。令 Ω  = Ω ∪ Γ ，假设f  y  为定义在紧实的研究域 Ω  上的连续函数，定义矩形域B为包含域  Ω  的一个研究域，函数g  y  为f  y  在域B上的延续，并且在域B/ Ω  内几乎处处连续且有界。对于任意点 y  y 1，y 2 ∈ Ω  ，定义函数F  y   为

F  y  y 1，y 2  = ∫   y 1  ag  t  t，y 2   d t （20）

其中，  y  y 1，y 2 ∈ Ω  ，a=y y 1，y 2 為有限函数， t t，y 2  为域B 内的点，并且设

F   y  =F  y    e   1， y  y 1，y 2 ∈ Ω   （21）

式中：  F   y  为对于y 1∈ Ω  是连续可微的，  e   1是笛卡尔坐标系中的单位基向量且  e   1= 1，0  ，并且

d  F （ y ）  d y 1 =f（ y ）  e    l SymbolQC@· F （ y ）=f（ y ）    y ∈ Ω   （22）

理论2：假设研究域  Ω 为一个有界平面区域，具有 Lipschitz 边界 Γ 。令 Ω  = Ω ∪ Γ ，假设f  y  为定义在紧实的研究域 Ω  上的连续函数，定义矩形域B为包含域 Ω  的一个研究域，函数g  y  为f  y  在域B上的延续，并且在域B/ Ω  内几乎处处连续且有界。对于任意点y y 1，y 2 ∈ Ω   ，可得

F  y  y 1，y 2  = ∫   y 1  ag  t  t，y 2   d t （23）

其中，  y  y 1，y 2 ∈ Ω  ，a=y y 1，y 2 且为有限函数，  t  t，y 2  为域B 内的点。

进而可以得到

∫  Ω f（ y ） d  Ω （ y ）=∮  Γ F（ y ）n 1（ y ） d  Γ （ y ） （24）

式中： n 1为边界 Γ 上的法向矢向量 n 在y 1 方向上的分量。

理论3： 假设研究域 Ω 为一个有界平面区域，具有 Lipschitz 边界 Γ 。令 Ω  = Ω ∪ Γ ，假设f y 为定义在紧实的研究域 Ω  上的连续函数，定义矩形域B为包含域  Ω  的一个研究域，函数g y 为f y 在域B上的延续，并且在域B/ Ω  内几乎处处连续且有界。函数 k  x ， y   为以域B内点 x 为中心的弱奇异核函数，对于任意点y y 1，y 2 ∈ Ω   ，可得

F  x ， y  y 1，y 2  = ∫   y 1  ag  t  t，y 2  k  x ， t  t，y 2   d t （25）

其中  y  y 1，y 2 ∈ Ω  ，a=y y 1，y 2 且为有限函数， t  t，y 2 为域B 内的点。

进而可以得到

∫  Ω f（ y ）k（ x ， y ） d  Ω （ y ）=∮  Γ F（ x ， y ）n 1（ y ） d  Γ （ y ） （26）

式中： n 1为边界 Γ 上的法向矢向量 n 在y 1 方向上的分量。

2.2 直线积分法

利用理论3，可以将域积分转换为边界积分。简单起见，将所有的积分起始点定在边界同一个平面上  y 1=c ，也就是说，a y 2 =c，c 可为任意常数值。当将边界离散化为 N 个单元时，式（26）则转化为

∫  Ω f（ y ）k（ x ， y ） d  Ω （ y ）=  N  i=1  ∫   Γ  i F（ x ， y ）n 1（ y ） d  Γ  i（ y ）  （27）

其中，  Γ  i为第i 个边界单元，并且有

F  x ， y  y 1，y 2  = ∫   y 1  cg  t  t，y 2  k  x ， t  t，y 2   d t  （28）

通过高斯积分法即可计算每个单元上的积分，但是在式（26）中仍然存在弱奇异积分。并且事实上，式（26）中的积分仍为由边界单元和平面  y 1=c  构成的区域的域积分。此时积分可以分为两种：常规积分和弱奇异积分。一般而言，对于单元 E ，产生弱奇异积分是因为积分点处在由该单元构成的积分域，因而积分线和单元 E 会出现一个交点，即为弱奇异积分的积分点，该弱奇异积分可以通过坐标转换的方法消除。这样式（26）中的域积分可表达为

∫  Ω f（ y ）k（ x ， y ） d  Ω （ y ）=  M  i=1  F i  x ， y  i n i 1  y  i w i  （29）

以及

F i  x ， y  i y i 1，y i 2  = ∫   y  i  1  cg  t  t，y i 2  k  x ， t  t，y i 2   d t  （30）

式中：   y   i y i 1，y i 2 為第i个边界积分点，M为积分点的总个数，w i和n i 1为第i个积分点的权重和在y 1 方向上的单位法向量。通过将每个单元内积分点产生的直线上的一维线积分相加即可得到域积分的结果。

为了提高式（29）的计算效率，本文进一步采用了背景网格将积分线划分为子线段，式（29）则可写为

∫  Ω f（ y ）k（ x ， y ） d  Ω （ y ）=  M  i=1  n i 1（ y ）w i∫  L i g（ y ）k（ x ， y ） d y 1 （31）

式中： M为子积分线段集的总数，L i为第i个子积分线，w i和n i 1为第i个子积分线段L i的权重和在y 1 方向上的单位法向量。

采用背景网格的具体方式为，构造一个能够包含研究域的最小正方形，保证所有边界节点和积分线包含于该正方形，定义该最小正方形为0级根网格，然后利用四叉树将根网格划分为四个等大小的子网格，定义为1级背景网格。按这种方式继续划分下去，从 L级网格得到L+1的背景网格，当第n 级子背景网格包含的积分线的数量不大于预设的数量时，即可停止划分。对于未能包含于一个子网格的积分线进行分段，保证所有积分线仅存在于一个子网格中，最后，删除不包含单元节点和积分线的子网格。没有下一级子网格的背景网格称为叶子。这些由四叉树构造的叶子即可对子积分线进行积分计算。

2.3 直线积分边界元法

直线积分边界元法为直线积分法和边界元法的结合，相较于传统的边界元法，在面对域积分时，仍能够保持降维的优点。本文边界积分方程中出现的域积分式（11），（18）和式（19）可以进一步转化为以下形式：

D 1 =∫  Ω  Φ  i  x ， y  βθ  y   d  Ω   y         =  M  i=0  n i 1（ y ）w i∫  L i  Φ  i  x ， y  βθ  y   d y 1 （32）

D 2 =∫  Ω  Ψ   ij   x ， y  βθ  y   d  Ω   y           =  M  i=0  n i 1（ y ）w iJac i∫  L i  Ψ   ij   x ， y  βθ  y   d y 1 （33）

D 3 =∫  Ω  Ψ   ij   x ， y  βθ  x   d  Ω   y           =  M  i=0  n i 1（ y ）w i∫  L i  Ψ   ij   x ， y  βθ  x   d y 1 （34）

显然，本文出现的域积分在直线积分边界元法的转化下，都变成了包含一维线积分的边界积分。

3 数值验证

为了验证直线积分边界元法的有效性和精度，本文采用两个例子进行验证。第一个例子为一个承受温度应力的矩形梁，并已知其解析解，进而可以验证本文所采用方法的精度。第二个例子为一个混凝土重力坝，计算结果将与有限元法模拟结果进行对比，以验证本方法在考虑温度应力的大坝静力分析中的有效性。

3.1 矩形梁的热弹性分析计算

如图1所示，该矩形梁的长度 L 为5，宽度 W 为3，弹性模量 E 为12 000 MPa，泊松比 ν 为0.25，热膨胀系数 k 为0.000 015 K  -1 。三边铰支，一边自由，温度场呈二次函数分布，具体表达式为

θ y =s 2y 2+s 1y+s 0 （35）

式中： s 0=0，s 1=-50，s 2=50 。

相应的位移和应力的解析解为

u y（y）= 1+v 1-v k  1 3 s 2 y 3+ （ W 2 ）  3 +

1 2 s 1 y 2- （ W 2 ）  2 +s 0 y+ W 2     （36）

σ  xx =- E 1-v kθ （37）

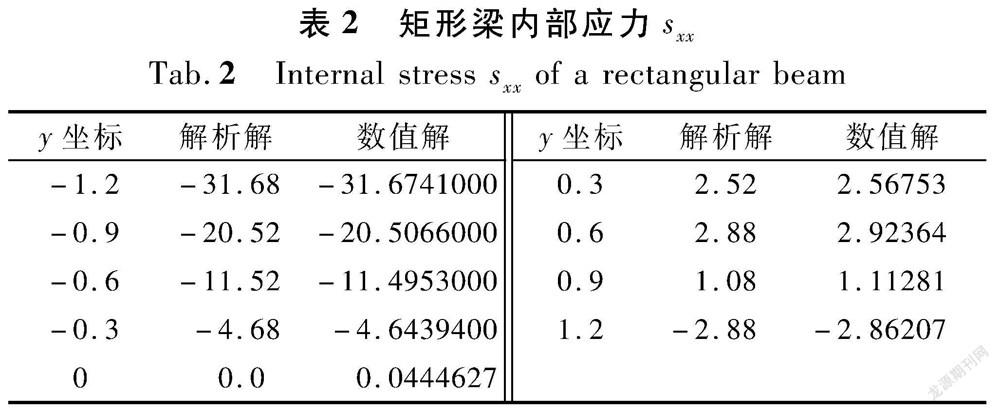
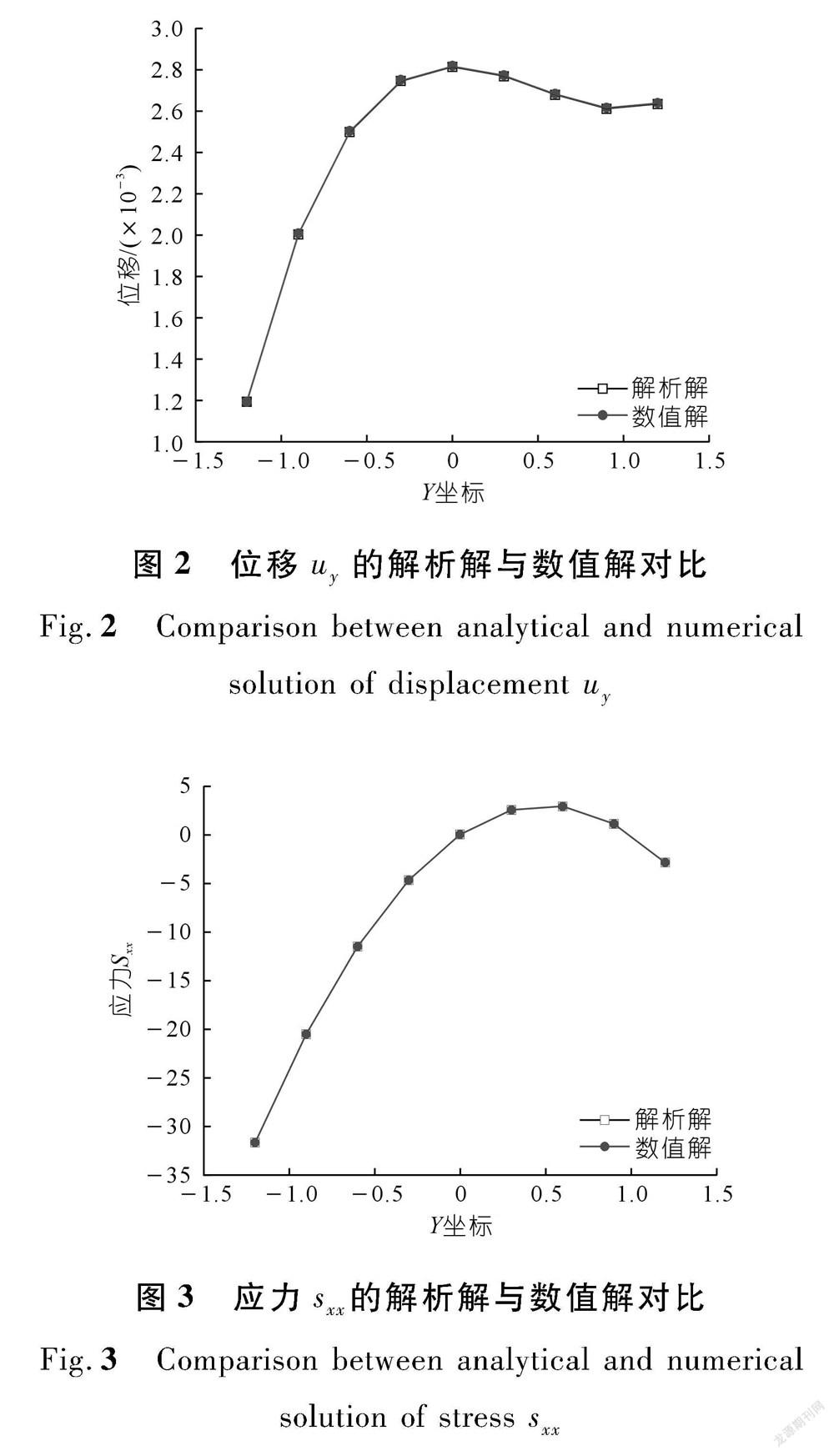
本算例中将梁的边界离散为仅80个单元，并将利用直线积分边界元法进行计算得到的结果与解析解进行对比。选取了直线 x =0上的9个内部点作为对比，具体结果分别列于表1和表2。结合图2和图3，可见数值解与解析解高度吻合，进而证明了直线积分边界元法的有效性和高精度。

进一步地，为了验证直线积分边界元法的精确性以及收敛性，现在将梁模型的边界分别划分为8，12，20，28，40，80，160，320个单元，并且利用以下公式计算样本点的相对误差

R=    N  i=1    u e i-u n i   2 /   N  i=1    u e i   2   （38）

式中： u e i和u n i分别代表解析解和数值结果，N 代表边界离散单元个数。

具体计算结果如表3所列。显然，随着边界离散单元个数的增加，相对误差逐渐减小，并且在单元数仅为8，相对误差就达到了0.96%，足以见本文方法的精度之高。

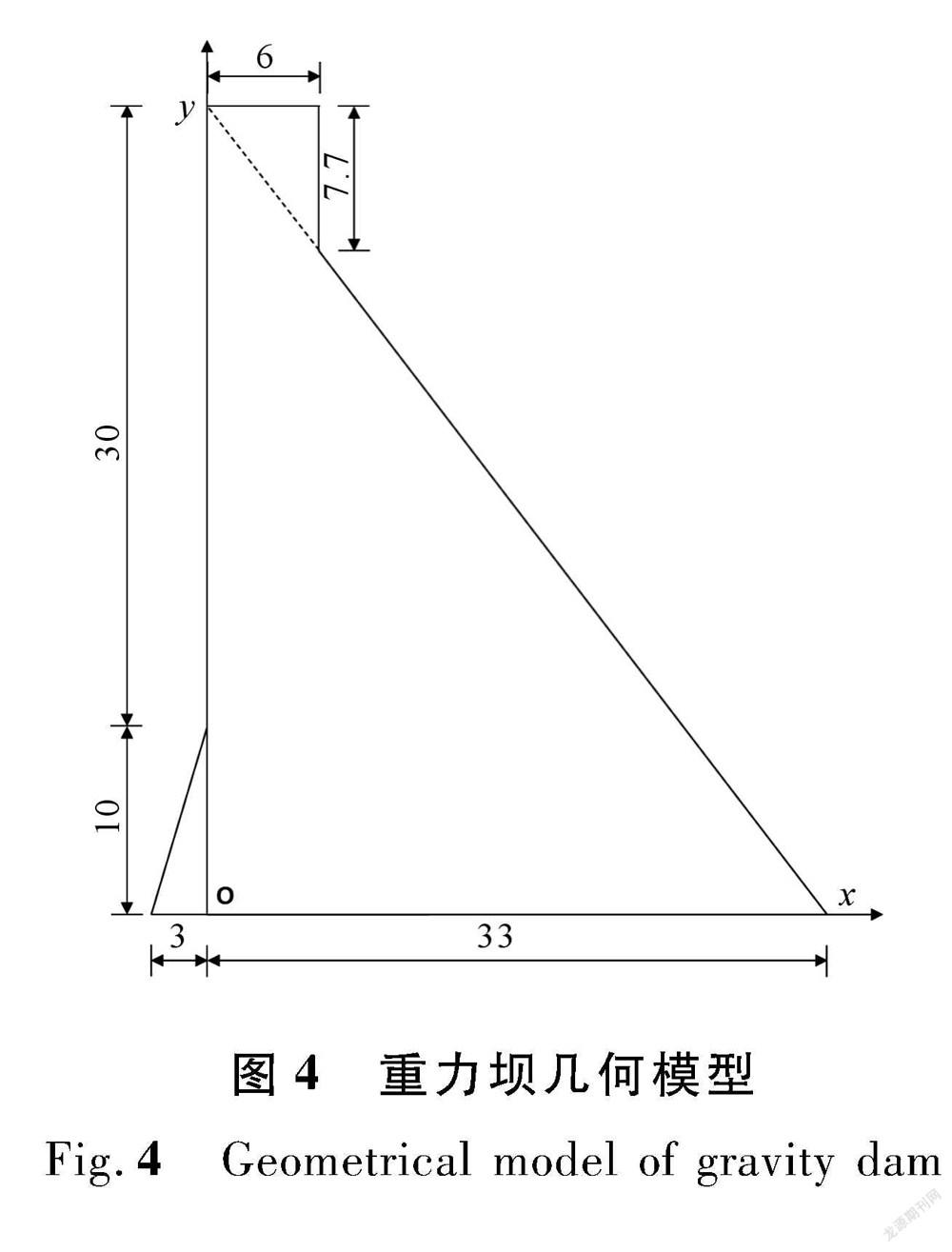
3.2 受温度荷载的大坝模型

重力坝模型具体几何尺寸如图4所示。泊松比为0.3，弹性模量为35 000 MPa，热膨胀系数为 0.000 015 K  -1 ，大坝底部为完全约束，其余边界自由。并且假设坝体承受65 ℃的高温冲击。

为了验证本文方法的正确性，在该数值模型的结果对比中，选取了在直线 x =3上的21个内部点，采用有限元模型与直线积分边界元法计算结果进行对比，如图5所示。计算所得的应力值 s  xx  与有限元计算方法高度相符，证明了本文方法的正确性。

4 结 论

边界元法的主要优势是可以将研究问题降低一维，并且已经成功地应用于静力学分析。本文的主要研究内容是利用边界元法进行热应力问题数值分析。但是由于考虑了温度对应力场的影响，在热应力的边界积分方程中出现了域积分项，为此本文提出采用一种新的直线积分边界元法。該方法将直线积分法和边界元法相结合，能够将域积分转化为包含一维积分的边界积分，进而延续了边界元法只需对边界进行离散的优势。为了验证本文方法的正确性，首先利用一个有解析解的梁结构进行了验证对比，验证了本文方法的高度精确性。此外，本文还将其运用到大坝结果的热应力分析当中去，通过与有限元法的对比，进一步验证了本文方法的可行性。

参考文献：

[1]  ISHIKAWA  M.Thermal stress analysis of a concrete dam[J].Computers&Structures，1991，40：347-352.

[2] NOORZAEI J，BAYAGOOB K H，THANOON W A，et al.Thermal and stress analysis of Kinta RCC dam[J].Engineering Structures，2006，28：1795-1802.

[3] 肖汉江，李祖民.考虑自生体积变形计算混凝土的温度应力[J].人民长江，1998，29（2）：4-6.

[4] 张锐，周伟，唐涛.构皮滩混凝土高拱坝全过程温度应力仿真分析[J].人民长江，2008，39（15）：74-77.

[5] WANG  Q，ZHOU W，CHENG Y，et al.A NURBS-enhanced improved interpolating boundary element-free method for 2D potential problems and accelerated by fast multipole method[J].Engineering Analysis with Boundary Elements，2019，98：126-136.

[6] ZHOU  W，LIU B，WANG Q，et al.Formulations of displacement discontinuity method for crack problems based on boundary element method[J].Engineering Analysis with Boundary Elements，2020，115：86-95.

[7] ZHOU W，LIU B，WANG Q，et al.NURBS-enhanced boundary element method based on independent geometry and field approximation for 2D potential problems[J].Engineering Analysis with Boundary Elements，2017，83：158-166.

[8] 陈亮亮，李建华，王建祥.直接边界元法在无限深透水地基渗流中的应用[J].人民长江，2010，41（1）：35-37.

[9] DAVEY K，ALONSO RASGADD M T.Integration over simplexes for accurate domain and boundary integral evaluation in boundary element methods[J].Computers & Structures，2004，82（2）：193-211.

[10]  CHEN C S，BREBBIA C A，POWER H.Dual reciprocity method using compactly supported radial basis functions[J].Communications in Numerical Methods in Engineering，2015，15：137-150.

[11] PARTRIDGE P W，BREBBIA C A.Computer implementation of the BEM dual reciprocity method for the solution of general field equations[J].International Journal for Numerical Methods in Biomedical Engineering，2010，6：83-92.

[12] ZHU S，SATRAVAHA P，LU X.Solving linear diffusion equations with the dual reciprocity method in Laplace space[J].Engineering Analysis with Boundary Elements，1994，13：1-10.

[13] NOWAK A J，BREBBIA C A.The multiple reciprocity method.A new approach for transforming BEM domain integrals to the boundary[J].Engineering Analysis with Boundary Elements，1989，6：164-167.

[14] WANG Q，ZHOU W，CHENG Y，et al.A line integration method for the treatment of 3D domain integrals and accelerated by the fast multipole method in the BEM[J].Computational Mechanics，2016，59：611-624.

[15] WANG Q，ZHOU W，CHENG Y，et al.Line integration method for treatment of domain integrals in 3D boundary element method for potential and elasticity problems[J].Engineering Analysis with Boundary Elements，2017，75：1-11.

[16] GAO X，ZHENG B，YANG K，et al.Radial integration BEM for dynamic coupled thermoelastic analysis under thermal shock loading[J].Computers & Structures，2015，158：140-147.

（編辑：郑 毅）

Thermal stress analysis based on line integration boundary element method

LIU Biao 1，GAO Yu 2，LI Tongsheng 2，WANG Qiao 1，ZHOU Wei 1

（ 1.School of Water Resources and Hydropower Engineering，Wuhan University，Wuhan 430072，China; 2.Datang Xuanwei Hydropower Development Co.，Ltd.，Qujing 655400，China ）

Abstract：

As a semi-analytical method，boundary element method （BEM） has the advantage of dimension reduction，which means this method only need to disperse the boundary for the research field.However，when it comes to solving the thermo-elastic problems，the domain integral will appear in the boundary integral equations.In order to ensure the advantage of BEM，the line integration method （LIM） is used to transform the domain integral into the boundary integral based on the divergence theorem.The boundary integral can be calculated by the boundary element with integral points.An integral line can be constructed for each integral point，and the domain integral can be calculated by the line integral on the integral line.In order to obtain higher accuracy，the integral line can be cut into sub-lines by using the background cell.This method feasibility and accuracy is proved by a thermal-elastic analysis of a rectangular beam and thermal stress analysis of a gravity dam.

Key words：

line integration boundary element method;dimension reduction;domain integrals;thermal stress