基于梯度自适应优化的入库流量数据平滑算法研究

陈建 李允军 王建平 吴善锋

摘要： 为了解决入库流量等时序数据跳变而影响对数据变化趋势规律判断的问题，结合水量平衡原理计算入库流量现实存在“跳变”的局限性，提出了梯度自适应迭代平滑算法，设计了数据序列光滑度评价计算方法，并阐述了其详细的计算原理和计算步骤。以三峡水库实际计算入库流量为例，将梯度自适应迭代平滑算法的平滑过程分别与3点、5点、7点线性平滑，5点、7点二次函数拟合平滑，5点、7点三次函数拟合平滑的结果进行對比。结果表明：该算法在入库流量平滑计算中具有较好的表现;三峡水库两段比较具有代表性的2月份和4月份小时计算入库流量数据序列经平滑计算后，数据序列的平均光滑度分别达到了0.958 4和0.980 3。该算法能够很好地适应原始数据光滑度较差的序列平滑计算，具有很好的实际应用推广价值。

关 键 词：入库流量; 数据平滑; 梯度自适应迭代平滑算法; 数据序列光滑度

中图法分类号：  P33

文献标志码：  A

DOI： 10.16232/j.cnki.1001-4179.2022.03.014

 0 引 言

入库流量的“大振幅”跳变会直接影响水库调度运行决策过程中对水库来水趋势的判断，也不符合实际情况，为了能够较为清晰地判断水库来水过程趋势，需要对随机性跳变的时间序列数据进行平滑校正处理。大多数水库的入库流量难以通过直接测量获取，目前普遍的方法是基于水量平衡法，根据水库坝上水位计算出库流量和水位库容曲线，反推入库流量。特别是对于大型水库而言，水库坝上水位的“振荡”误差导致入库流量值误差较大，以湖南省大东江、柘溪和凤滩3个水库为例，计算1 h入库流量，在水库坝上水位误差在0.01 m时，大东江水库的入库流量误差为174～488 m 3/s、柘溪水库的入库流量误差为12～750  m 3/s 、凤滩水库的入库流量误差为27～111 m 3/s。入库流量的误差呈现以下几个特点：① 入库流量误差跟坝上水位值相关，坝上水位值越大，同样的水位差产生的误差越大，表现在计算入库流量过程上，不同的季节入库流量的“锯齿”呈现不同的变幅现象;② 水库的库容越大或者同样水位差下的库容越大，入库流量出现的误差越大;③ 坝上水位受采样地点、采样点数和水库闸门开闸的水位波动等影响，难以采集准确代表水库水位的水位值;④ 水库水位测量仪目前大多能测量的最高精度为0.01 m。基于以上特点，难以从测量手段上解决入库流量的计算准确性问题。有的学者采用动库容计算  [1-3] 的方式进行计算，但效果并不显著，一方面投入建站成本比较高，目前大量水库不具备采用动库容计算的条件;另一方面跳变依然比较严重。水位变幅限制、多水位站平均等计算方法也能够在一定程度上降低跳变的程度，但是也有一定的局限性  [4] 。目前基本上是将基于理论的入库流量过程当作一个渐变过程线，采用数学平滑算法对计算的入库流量结果进行平滑处理  [5-7] ，主要的平滑算法有3点、5点、7点线性平滑，5点、7点二次函数拟合平滑，5点  [8] 、7点三次函数拟合平滑，最小二乘曲线  [9] ，样条插值平滑  [10] ，小波变换滤波  [11] 以及一些其他的滤波算法  [12] 。这些算法在处理数据平滑方面都有一定的作用，但是在各种数据情形下表现不一。基于此，本文通过设计一种全新的梯度自适应迭代平滑算法，以适应各种特性的入库流量过程的数据平滑，并以三峡水库实际计算入库流量为例，将该算法的平滑过程分别与3点、5点、7点线性平滑，5点、7点二次函数拟合平滑，5点、7点三次函数拟合平滑的结果进行对比。

1 梯度自适应迭代平滑算法原理

梯度自适应迭代平滑算法是一种将曲线描绘成某一种抽象的“形状架构”，通过迭代优化调整，最终使得曲线的所有段都满足一种抽象的“形状架构”特征。基于梯度的架构采用的是一种基于类似于“三角形”架构，找出或者确定一个中间拐点，随之确定其前后的顶点数值，如果它们之间的梯度形状满足设置确定的要求，就认为该数据的变化满足梯度要求，如果不满足其梯度形状参数的条件，则对其形状朝着满足梯度形状参数的要求方向进行微调整，不断地进行迭代优化调整，最终使整个曲线满足梯度形状条件，过程优化结束，调整后的曲线即是平滑过后的曲线，其计算优化步骤如下。

（1） 算法定义参数包括：曲线最小适应弧度（γ   min  ）、修正因子（λ）、衰减因子（δ）、最大循环次数（Lp   MAX  ）、滑动窗口大小（W   SIZE  ）、滑动窗口维度（W   DIM  ）。

（2） 输入需要进行平滑的时间序列（Time Series），数据长度为 n，整个记为T n（t 0，t 1，t 2，…，t n）。

（3） 确定滑动窗口的大小 W   SIZE ，窗口的大小值最好为奇数。

（4） 记录第1次进行时间序列 T n 平滑优化计算的时次初始化为 count =0。

（5） 每次扫描都从序列 T n的第0个值开始，初始化定义i=0。

（6）  从时间序列T n的第i个数进行计算，窗口范围内的数据序列可以记为T  i～i+W   SIZE   ，计算窗口内的数据序列T  i～i+W   SIZE   的平均值，记为AVGV  W   SIZE   。

（7）  将滑动窗口内的数据点T  i～i+W   SIZE   按照数值大小聚类归并为3个数据集，记为[A，B，C]。

（8）  计算滑动窗口范围内的3个数据集三角形特征值，定义三角形3个顶点值分别为 A（0， y   0 ），B（0.5， y   1 ）和C（1， y   2 ）， y   0 ， y   1 ， y   2 分别是滑动窗口内时间序列提炼出的3个顶点的歸一化后的序列值 ，图1、图2为三角形6种不同的表现形式： [A，B0，C0]、[A，B1，C1]、[A，B2，C2]、[A，B3，C3]、[A，B4，C4]、[A，B5，C5] 。

（9） 顶点A，B，C组成三角形△ABC，三角形的3条边的边长分别记为L  AB 、L  BC 和L  AC ，其中角B记为∠B，计算∠B的弧度，记为γ  ∠B ，弧度计算公式如下：

γ  ∠B = （L 2  BC +L 2  AB -L 2  AC ） 2L  AB L  BC   （1）

（10）  判断三角形△ABC为“∧”形还是“∨”形，判断依据：如果 y 0+y 2 2 >y 1，则三角形△ABC为“∨”形;如果 y 0+y 2 2 <y 1，则三角形△ABC为“∧”形;如果 y 0+y 2 2  = y 1，那么此3点在一条直线上。

（11）  如果△ABC为“∧”形，并且γ  ∠B 小于γ   min  ，则按照坦化“∧”形趋势的方向调整A，B，C 3个结点数据集的数值，增大A和C两个结点数据集的数值，减小B结点数据集的数值，具体减少的数值记为 Δ Value=λ× max （y 0，y 1，y 2），同时A和C两个结点的数据集的数值增加的数值记为 Δ Add= Δ Value/2。

（12）   如果△ABC为“∨”形，并且γ  ∠B 小于γ   min  ，则按照坦化“∨”形趋势的方向调整A，B，C 3个结点数据集的数值，减小A和C两个结点数据集的数值，增加B结点数据集的数值，具体增加的数值记为 Δ Value=λ× min （y 0，y 1，y 2），同时A和C两个结点的数据集的数值减小的数值记为 Δ Minus= Δ Value/2。

（13） 分别按照增加和减小的数值，对应调整 A，B，C  3个结点数据集的数值， 更新时间序列T n对应位置上的值，判断是否已经是该序列最后一个窗口，如果为“否”，则按照滑动窗口维度W   DIM  滑动到序列的下一个窗口T  i+W   DIM  ～i+W   DIM  +W   SIZE   ，i=i+W   DIM  ，重复步骤（5）。

（14）  如果为“是”，则 count=count+1;判断count 值是否大于 Lp   MAX  ，如果“是”，则退出循环，返回经过优化平滑的时间序列T n，如果为“否”，则重复步骤（4）。

整个算法的流程如图3所示。

2 序列平均光滑度计算

本文试图定义一种方法，可以评价一个数据序列经过数据平滑过后，平滑程度或者效果的评价指标，在实际的数据序列中没有真实的平滑结果存在，因此不能将平滑的结果与“真实”结果比较，只能与未进行平滑的原始数据序列进行比较，找到一种可以评价数据平滑程度的计算方法。目前有研究学者提出了数据平滑度、光滑度  [13] 等概念，与评价一种数据平滑方法的好坏程度并不是很吻合，本文提出一种计算数据序列光滑度的计算方法，用于评价数据序列被平滑过后与原数据相比其平滑程度。

定义一个数据序列为X（x 1，x 2，x 3，…，x n），评价一个数据序列的平滑度可以定义为计算离散数据点之间的斜率之差，具体计算步骤如下。

（1） 对数据序列进行归一化处理，找出X序列的最大值x   max  ，X序列归一化之后的序列为X′（x′ 1，x′ 2，x′ 3，…，x′ n）。

（2） 相邻数据点的平滑度可以定义为曲线的斜率之差的平方，理论上当相邻点关系在同一条曲线上时，数据点之间的斜率之差为0，这时数据是最平滑的，是一条直线。简单的计算平滑度指标并没什么应用意义，本文通过平滑度值的比较来衡量原始曲线被平滑的程度，具体计算方式如图4所示。

从图4可知，  x′ i 的数据平滑度计算公式为

Smoothness i=  1- （x′ i-x′  i-1 ） 2-（x′  i+1 -x′ i） 2    2 （2）

整个数据序列X′（x′ 1，x′ 2，x′ 3，…，x′ n）的平均平滑度计算公式为

Smoothness=  1 -     n-1   i=1    （x′ i-x′  i-1 ）  2- （x′  i+1 -x′ i）  2  n-2    2  （3）

计算条件为 n>2，Smoothness 值越大，代表平滑度越好，等于1则为直线。

3 入库流量平滑计算案例分析

3.1 入库流量计算方法

入库流量很难通过直接测量获取，目前常用的入库流量反推计算方法是基于水量平衡原理，利用期末期初坝上水位、时段出库流量和水位库容曲线进行反推计算时段入库流量  [14] ，计算公式如下：

Q  入库 Δ t = f（Z   Δ t末 ）-f（Z   Δ t初 ）  Δ t +Q  出库 Δ t  （4）

式中： Δ t表示时段步长，Q  入库 Δ t 表示时段入库流量，Z   Δ t初 表示时段初水库水位，Z   Δ t末 表示时段末水库水位， f（Z   Δ t初 ） 表示时段初库水位对应的库容，f（Z   Δ t末 ）表示时段末库水位对应的库容，Q  出库 Δ t 表示时段出库流量。

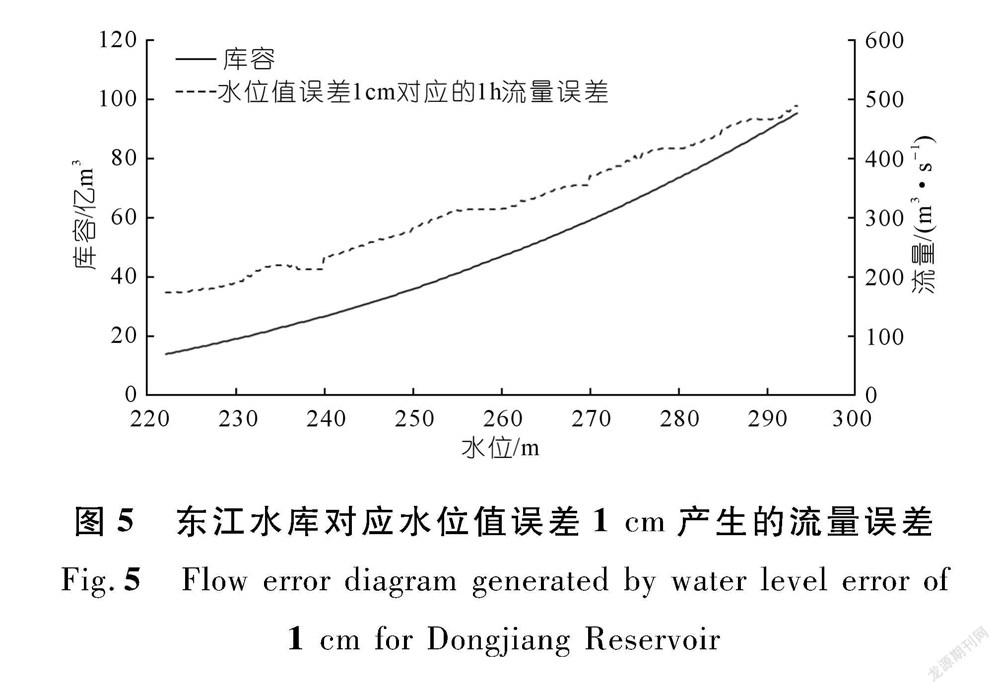
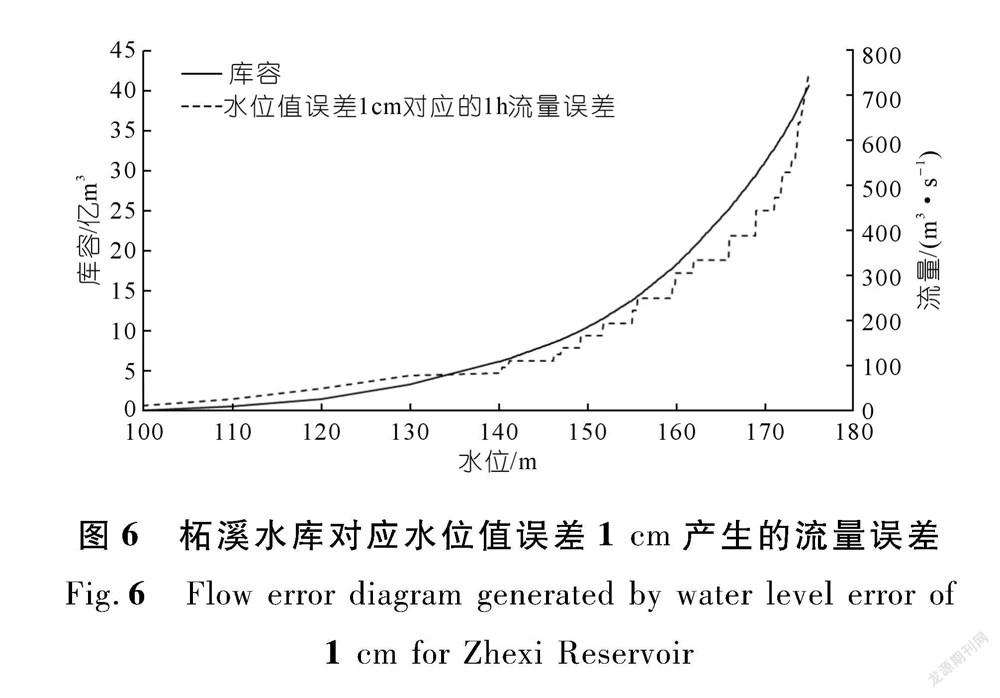
采用这种方法反推入库流量对水库水位的精度要求很高，而往往难以做到。本文以华中区域的东江、柘溪水库和三峡水库为例进行计算，东江水库是多年调节水库，柘溪水库和三峡水库都属于不完全年调节水库。下面以东江水库和柘溪水库为例进行测算，水库水位误差1 cm时对计算入库流量产生的影响如图5～6所示。

结合公式（2），从图5、图6可知：水库水位越高，1 cm误差造成的入库流量误差越大。东江水库的流量误差范围174.0～487.0 m 3/s，柘溪水库的流量误差范围12.5～750.0 m 3/s，说明水库不同时期不同运行水位下的反推入库流量的波动程度会有较大的区别，水库水位的精度对水库入库流量影响巨大。

水库受机组开关机、闸门启闭和船闸启闭等综合影响，较容易产生水位“假潮”现象  [15] ，在短时间内测量的水位会出现较大的波动，有时候波动会高达20 cm，这就造成了有时候会前后时段入库流量出现波动很大，甚至出现入库流量为负值的情况  [16] 。

3.2 不同平滑算法结果对比分析

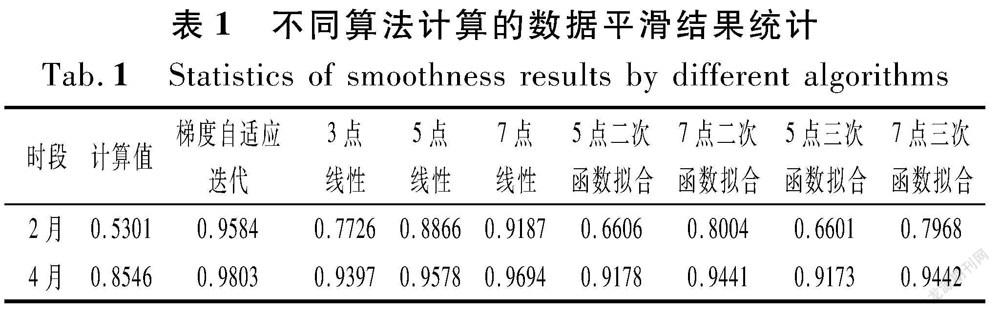
本文中将新设计的梯度自适应优化算法与目前常采用的3点、5点、7点线性平滑，5点、7点二次函数拟合平滑，5点、7点三次函数拟合平滑进行对比（见表1），分别取三峡水库的非汛期2月和4月动库容计算入库流量数据，采用上述几种平滑方法进行平滑计算，平滑结果如图7所示。

从表1中可以看出：不管是2月份数据，还是4月份数据梯度自适应迭代算法的平均光滑度是最高的。2月份的数据原始计算值的平滑度为0.530 1，经过平滑后达到了0.958 4;其次是7点线性平滑达到了 0.918 7 。4月份的原始数据的光滑度为0.854 6，从整体上看所有方法的平均光滑度都达到了0.9以上，其中数据梯度自适应迭代算法的平均光滑度为0.980 3，所有的方法都有平滑效果，只是平滑的程度不一样。

图7中是分别采用以上8种算法进行平滑过后的三峡水库2月份的小时计算入库流量，从上面的分析可以看出，在类似2月份这种枯水期或者平水期，实际上的来水过程是比较平稳的，但是由于受“水位波动”的影响，造成出现大量的“假峰”、“假谷”现象和“锯齿”现象。从图7中还可以看出，梯度自适应迭代平滑算法、5点线性平滑和7点线性平滑算法平滑效果比较明显，其中梯度自适应迭代平滑算法的平滑效果是最佳的，而且对于“锯齿”现象越明显，其效果越明显。从上面的算法结果比较情况来看，二次函数和三次函数拟合在平滑方面起的作用比较有限，相比而言，线性函数的作用 较大。

4 结 论

本文分别选取三峡水库波动非常剧烈的2月和波动比较平缓的4月为例，经过实际应用验证，得出以下主要结论：

（1） 梯度自适应迭代平滑算法具有良好的平滑自适应性，原始数据光滑度越差的数据相比其他方法，梯度自适应迭代平滑算法起到的平滑效果效果更加明显，其他的方法平滑效果相对不理想。

（2）  梯度自适应迭代平滑算法平滑效果较为稳定，在原始数据光滑度较好，局部光滑度较差的时候，梯度自适应迭代平滑算法具有稳定的平滑表现。

（3） 该算法相比其他的算法还有一个重要特点，它是满足数值序列整体平均值或者累计值不变的，采用该算法平滑处理后，入库流量只是实现了时段内的重新分配，满足水量平衡的要求。

（4） 经过算法对比和实际数据验证，该算法具有很好的推广应用价值。

参考文献：

[1]  张俊，闵要武，陈力，等.基于动库容曲线的水库调洪高水位查算方法研究[J].水文，2016，36（5）：63-68.

[2] 张俊，闵要武，陈新国.三峡水库动库容特性分析[J].人民长江，2011，42（6）：90-93.

[3] 闵要武，王俊，陈力.三峡水库入库流量计算及调洪演算方法探讨[J].人民长江，2011，42（6）：49-52.

[4] 王世策，胡晓勇.大型水库计算入库流量波动过大问题分析[J].安徽水利水电职业技术学院学报，2010，10（3）：19-21.

[5] 王俊莉.贵州乌江梯级水库入库流量计算分析及改进方法[J].水利水电快报，2015，36（4）：54-56，74.

[6] 唐春艷，彭继兵.基于变维滤波算法的Kalman最佳平滑器在滑坡监测数据处理中的应用[J].工程数学学报，2009，26（4）：586-592.

[7] 唐海华，陈森林，赵云发，等.三峡水库入库流量计算方法研究[J].中国农村水利水电，2008（4）：26-28.

[8] 武炜，陈标，吴剑锋，等.基于五点三次平滑算法的入库流量反推研究[J].水利水电技术，2013，44（12）：100-102.

[9] 張俊，廖胜利，程春田，等.基于最小二乘曲线的水电站入流平滑处理[J].水电能源科学，2011，29（4）：55-56，154.

[10]  杨海星，黎浩，曹净.基于样条函数的监测数据平滑算法与Matlab实现[J].长春工程学院学报（自然科学版），2018，19（3）：92-97，120.

[11] 田鑫.基于离散小波变换的海洋工程数据降噪研究[D].大连：大连理工大学，2015.

[12] 杨金标，舒凯，张后来，等.水库水量平衡计算中消除水位跳变影响的过滤算法[J].人民长江，2019，50（8）：98-102.

[13] 郑锋，魏勇.提高灰建模数据列光滑度的一种新方法[J].统计与决策，2007（18）：37-38.

[14] 刘章君，郭生练，钟逸轩，等.入库洪水计算方法及研究进展综述[J].中国农村水利水电，2016（11）：1-6，11.

[15] 刘超，彭艳华，彭艳明，等.水位“假潮”现象平滑处理方法研究[J].长江工程职业技术学院学报，2011，28（1）：27-28，34.

[16] 王永峰，孟继慧.丰满水库调度有关基础资料问题的历史沿革[J].水利水电技术，2016，47（6）：56-59，79.

（编辑：谢玲娴）

Research on smoothing algorithm of reservoir inflow data based on  gradient adaptive optimization

CHEN Jian，LI Yunjun，WANG Jianping，WU Shanfeng

（ Nanjing Nari Water Resources Hydropower Technology Company，Nanjing 211000，China ）

Abstract：

In order to solve the problem that the jump of time series data such as inflow affects the judgment of the data change trend，we proved the limitation of "jump" in inflow based on the principle of water balance，proposed a smooth gradient adaptive iteration algorithm （SGAIA），designed a calculation method for evaluating the smoothness of data series，and expounded its detailed calculation principle and calculation step.Taking the actual inflow calculation of the Three Gorges Reservoir as an example，we compared the smoothing results of SGAIA with other methods，including 3/5/7-point linear smoothing algorithm，5/7-point quadratic function fitting smoothing algorithm，and 5/7-point cubic function fitting smoothing algorithm.The results showed that SGAIA has better performance in the smoothing of inflow data.Then we execute smooth calculation on two more representative data series of hourly calculated inflow of the Three Gorges Reservoir in February and April，and the average smoothness of the data series after smoothing calculation reached 0.9584 and 0.9803，respectively.SGAIA can be well adapted to data series smoothing calculation in case of poor original data smoothness.

Key words：

reservoir inflow;data smoothing;gradient adaptive iterative smoothing algorithm;smoothness of the data series