智能反射面辅助的星地融合网络鲁棒安全波束成形算法*

肖圣杰 林敏† 赵柏 林志 程铭

1) (南京邮电大学 通信与信息工程学院,南京 210003)

2) (国防科技大学 电子对抗学院,合肥 230037)

针对智能反射面辅助的星地融合网络,提出了一种基于窃听者非完美信道状态信息的鲁棒安全波束成形方法.首先,考虑到卫星利用点波束技术服务地球站,而地面基站通过多播技术服务多个地面用户,并且在两个网络实现频谱共享的情况,建立以系统总发射功率最小化为目标,基站用户服务质量和地球站安全可达速率为约束条件的联合优化问题;其次,为了求解该非凸问题,利用三角不等式和Holder 不等式推导出窃听者非完美信道状态信息条件下的输出信干噪比上下界;接下来,进一步提出了基于半正定规划和惩罚函数相结合的鲁棒波束成形和功率控制联合优化方法,以实现星地融合网络的安全可靠传输.最后,计算机仿真结果验证了本文所提算法的有效性和优越性.

1 引言

随着第五代移动通信系统在全球范围进入商业运营阶段,地面有线和无线网络开始为高密度人口地区用户提供即时、高速数据传输服务,但因地理条件和商业模式的限制,偏远地区的网络依然无法满足用户全域覆盖和泛在接入需求.跟地面无线通信系统相比,卫星通信具有覆盖范围广,对基础设施依赖小,不受地理条件限制等优点,可实现通信网络全球无缝覆盖,被认为是未来通信系统中不可或缺的一部分[1-3].为了充分利用地面无线系统建设和维护成本低的优点,以及卫星通信系统广域覆盖的优势,同时克服各自固有的缺点,研究人员提出了星地融合网络(satellite terrestrial integrated network,STIN)框架,并受到了学术界和工业界的广泛关注[4-6].

STIN 中普遍采用全频率复用技术以缓解频谱资源短缺问题,但这会带来严重的网络间干扰,同时卫星通信的广播特性和无线信道的开放特性也会导致系统存在巨大的窃听风险[7].因此如何降低同频干扰,提高通信安全性,充分释放星地融合异构网络的系统优势,成为了当前的一个研究热点.传统的无线通信安全主要通过传输上层加密实现,但随着云计算、量子计算等新技术的出现,基于计算复杂度的密钥安全体制面临着巨大的挑战.近几年来,采用多天线的波束成形(beamforming,BF)技术,通过对信号波束辐射方向的调整,能够有效增强期望用户接收信号质量并抑制信号泄露给非期望用户,降低同频干扰并提高信息传输的安全性能,从而备受国内外学者的青睐[8-12].其中,文献[9]和[10]重点关注了卫星和地面网络共存带来的影响,分别提出了一种卫星BF 方案和一种联合BF优化方案,以抑制网络间干扰.针对STIN 中信号的安全传输问题,文献[11]研究了存在单个窃听者的星地认知网络场景,并提出一种以安全能源效率最大化为目标的联合BF 优化方案.文献[12]进一步研究了存在多个窃听者的星地认知网络安全传输问题,且在假设窃听者信道状态信息(channel state information,CSI)非完美的情况下,提出一种迭代BF 算法以最大化系统信息和速率.

另一方面,新兴的智能反射面(intelligent reflecting aurface,IRS)技术,被认为是无线通信系统中实现物理层安全通信的前景技术之一.IRS 是一种由大量低成本、可重构的近似无源电磁反射元件构成的阵列平面,通过预编程控制器,可对入射电磁波的相位和幅度进行智能调整来提升系统的性能,并且其结构简单且功耗低,可灵活应用于多种无线通信场景[13-15].基于上述原理,文献[16]在下行认知无线电系统中引入多个IRS,在保证对主用户干扰功率小于门限值的条件下,最大限度地提高了次用户的信息可达速率.文献[17]和[18]分别研究了存在单个窃听者和多个窃听者场景下IRS 辅助的地面通信系统传输方案设计,通过联合设计基站的发送BF和IRS 的无源BF,最大限度地提高了合法通信链路的保密率.虽然前期已有文献对IRS技术在物理层安全方面的应用进行了深入的研究[16-18],但它们仅适用于地面无线网络,将IRS 技术应用于星地融合异构网络的工作才刚刚开始,还有很多工作有待完成.文献[19]首次将IRS 应用于STIN 中,在以窃听者SINR 最小化为目标的前提下,研究了卫星通信的物理层安全问题.然而,该文献仅考虑单个窃听者CSI 完全已知情况下的简单场景,且假设卫星仅配备了单根天线,导致该文献的工作存在较大的局限性.

针对上述问题,本文在仅已知窃听者非完美CSI 的情况下,提出了一种IRS 辅助的STIN 鲁棒安全BF 方法.与文献[19]相比,本文研究了一个更具普适性的多天线卫星受多用户窃听场景.首先,考虑到在卫星利用点波束技术服务地球站,而地面基站通过多播技术服务多个地面用户的同时向窃听者发送绿色干扰以抑制窃听,并且在两个系统实现频谱共享的情况下,建立了以系统总发射功率最小化为目标,地面用户服务质量和地球站安全可达速率为约束条件的联合优化问题;其次,为了求解该非凸问题,利用三角不等式和Holder 不等式推导出窃听者非完美CSI 条件下的输出信干噪比上下界;接下来,进一步提出了基于半正定规划和惩罚函数相结合的鲁棒BF和功率控制联合优化方法,以实现STIN 的安全可靠传输.最后,仿真结果表明了本文所提算法的有效性和优越性.

符号说明:E[·],数学期望;|·|,绝对值;CN(·,·),复高斯分布;‖·‖,向量范数;IN,单位矩阵;CN×M,N×M维空间;⊙,Hadamard 积;min(·,·),最小值;(·)H,矩阵共轭转置;(·)T,矩阵转置;(·)*,共轭;vec(·),矩阵矢量化;Tr(·),矩阵的迹;rank(·),矩阵的秩;λmax(·),矩阵的最大特征值;〈X,Y〉Tr(XHY) ;diag(·),矢量对角矩阵化.

2 系统模型

如图1 所示,本文研究了STIN 下行物理层安全通信场景,其中,卫星网络由一颗地球静止轨道卫星,一个地球站和N个非协作窃听者组成;地面网络由一个地面基站,一架搭载IRS 的无人机和M个地面用户组成.假设卫星配置具有K个馈源的单反射面天线,基站配置具有D个阵元的均匀线阵,IRS 为具有L1×L2个反射单元的均匀阵列,地球站和窃听者配置高增益抛物面天线,地面用户配置单天线.在卫星网络和地面网络共享频谱资源的情况下,卫星利用点波束技术服务地球站,同时受到窃听;基站通过IRS 扩大通信范围,服务地面用户并向窃听者发送友好干扰,以辅助卫星网络实现信息安全传输.此外,基站通过光纤链路和核心控制网相连,核心控制网作为控制中心,收集和管理各种信息,如链路CSI,用户QoS 需求,安全传输指标等,并控制着整个网络的运行与信息传输.

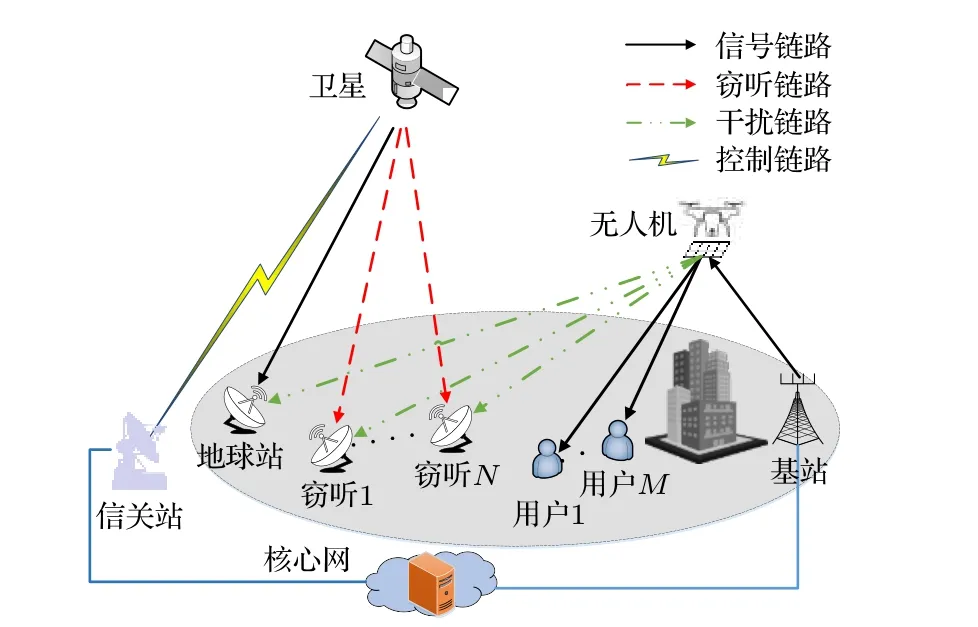
图1 系统模型Fig.1.The system model.

2.1 卫星通信信道模型

考虑路径损耗、雨衰减和波束增益影响,卫星与用户间下行信道可表示为[10]

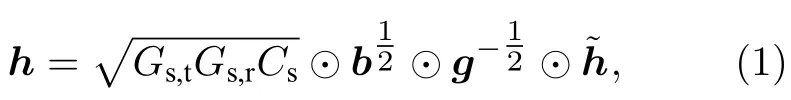
其中,Gs,t为卫星发射增益,Gs,r为卫星服务用户的抛物面天线增益.参考ITU 的建议[20],Gs,r表达式为

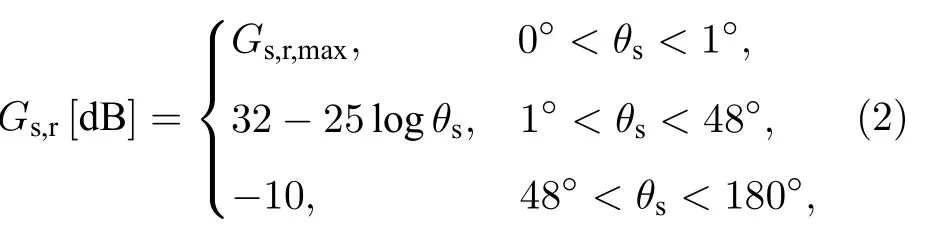
其中,Gs,r,max为抛物面天线轴向的最大增益,θs为用户相对于卫星的离轴角.在公式(1)中,Cs为卫星与用户间的自由空间损耗,可表示为

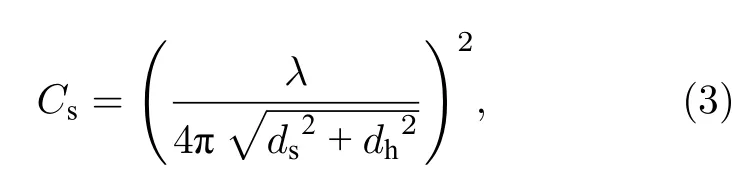
其中,λ为载波波长,dh为卫星高度,ds是用户到卫星覆盖区域中心距离.在公式(1)中,g∈CK×1表示雨衰系数矢量,其元素的dB形式服从对数正态随机分布1≤k≤K,μg和σg和卫星的通信频率、极化方式和用户的位置有关,K表示卫星阵列天线数,b∈CK×1表示点波束增益,其元素可以表示为

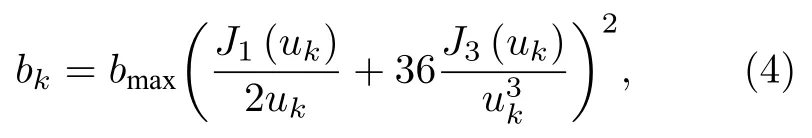
其中,bmax为卫星天线的最大增益,J1(·) 和J3(·)分别是1 阶和3 阶的第一类贝塞尔函数,uk2.07123 sinφk/sinφ3dB,φk表示用户相对于波束k的偏轴角,φ3dB为单侧半功率波束宽度.此外,在公式(1)中,由用户到达不同波束的相位差组成,其元素为其中,dk表示用户到第k个卫星馈源的距离.

2.2 IRS 信道模型

假设搭载有IRS 的无人机飞行高度高于通信环境中建筑物,基站信号通过IRS 反射给用户,使用空对地通信的方式,降低了阴影效应的影响,且一般存在较强的视距传输路径,故IRS 与用户的下行链路信道可表示为

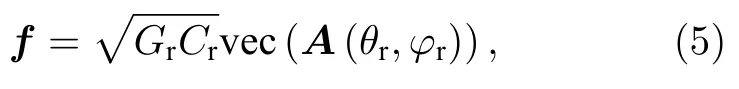
其中,Gr为用户的接收增益,Cr为IRS 与用户间的自由空间损耗,为IRS 信道矩阵,可表示为

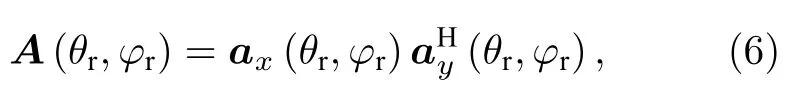
其中,θr和φr分别表示用户相对于IRS 的信号出发俯仰角和出发方位角,ax(θr,φr)和ay(θr,φr) 为IRS 的x轴和y轴导向矢量,分别表示为

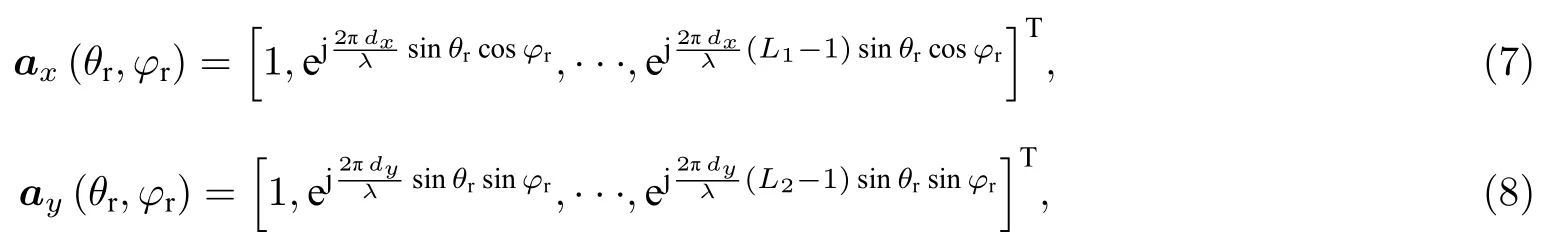
其中,dx和dy表示IRS 阵列x轴和y轴方向上的相邻反射单元物理间距,L1和L2分别表示IRS 阵列x轴和y轴方向上的反射单元数.

基站向空中的IRS 发送信号,考虑视距传输路径占主导地位,则基站到IRS 的信道可表示为

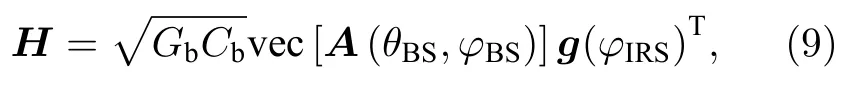
其中,Gb为基站发射增益,Cb为基站与IRS 间的路径损耗,A(θBS,φBS)为IRS 信道矩阵,θBS和φBS分别表示IRS 相对于基站信号的到达俯仰角和到达方位角,g(φIRS) 为基站信道矢量,可表示为

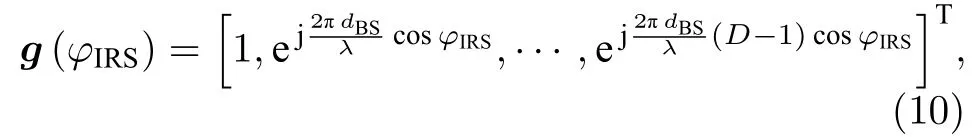
其中,φIRS为基站相对于IRS 的信号出发角,dBS为基站配置的均匀线阵相邻阵元间距,D表示基站阵列天线数.

2.3 用户信号模型

在实际情况中,卫星用户一般采用较高增益的天线以补偿长距离传输带来的大路径损耗,而地面移动终端采用低增益的全向天线,因此,不失一般性,本文不考虑卫星信号对地面终端的干扰[21].假设基站采用多播技术并通过IRS 向地面用户发送信号,以提高地面网络通信质量与频谱效率,则地面用户m接收信号为

其中,x(t)为基站发送给地面用户m∈{1,2,···,M}的有用信号,满足E[|x(t)|2]1 ;P为基站发射功率;为IRS到地面用户m的信道矢量;为IRS的对角相移矩阵,其中元素表示IRS 各单元对输入信号相位的旋转量;为基站到IRS 的信道矩阵;nb,m(t) 为地面用户m收到的零均值加性高斯白噪声.考虑到基站与IRS 使用点对点通信且其信道矩阵已知,为降低算法复杂度并尽可能提高IRS 反射信号质量,基站采用最大比传输方案获得归一化BF 权矢量wMRT∈CD×1.

卫星向地球站发送私密信号,同时考虑来自IRS的干扰信号,则地球站的接收信号为

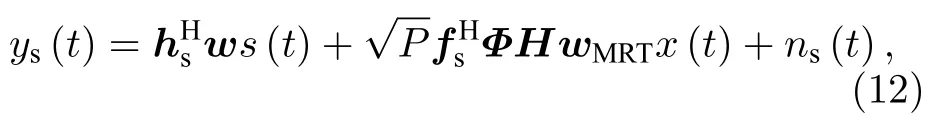
其中,s(t) 为卫星向地球站发送的私密信号,满足E[|s(t)|2]1;w∈CK×1为卫星BF 权矢量;hs∈CK×1为卫星和地球站之间的信道矢量;fs∈为IRS到地球站的信道矢量;ns(t) 为地球站收到的零均值加性高斯白噪声.

考虑有些情况下窃听者离地球站比较近,仅依靠卫星的BF 难以抑制窃听行为,故基站在服务地面用户的同时,向窃听者发送友好干扰,以协助卫星抑制窃听.故窃听者n的接收信号可表示为

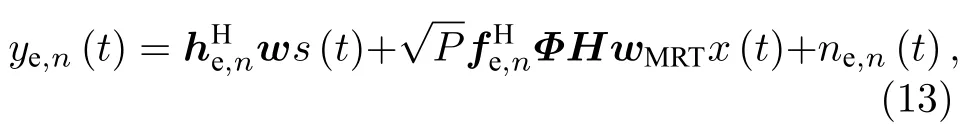
其中,he,n∈CK×1为卫星到窃听者n的信道矢量,为IRS到窃听者n的信道矢量,ne,n(t)为窃听者n收到的零均值加性高斯白噪声.根据公式(11),(12)和(13),地面用户m,地球站和窃听者n的输出信干噪比(signal-to-interference-plusnoise ratio,SINR)可分别表示为

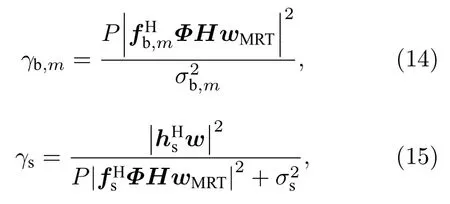
本节对所研究的STIN 系统模型和信道模型进行了介绍,如上所述,卫星通信存在被窃听风险,为提升STIN 的安全性能,本文在窃听者CSI 存在误差的条件下提出以最小化系统总发射功率为准则的鲁棒BF和功率控制联合优化方案.

3 安全传输方法设计方案

本文以STIN 总发射功率最小化为优化目标,通过联合优化卫星波束形成权矢量、基站发射功率及IRS 相移矩阵,实现STIN 中信息的安全传输.基于公式(14),(15),(16)且考虑窃听者信道存在的误差,受约束的系统总发射功率最小化问题可以表述为优化问题P1:

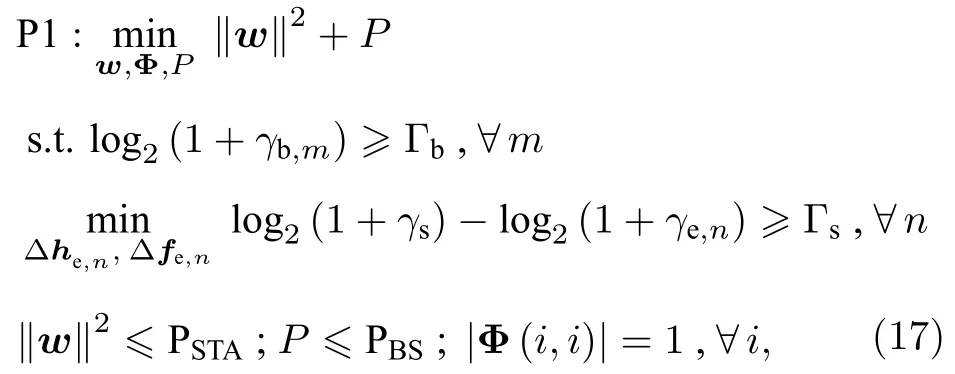
其中,Γb为地面用户可达速率门限;Γs为地球站安全可达速率门限;PSAT和 PBS分别为卫星和基站的最大发射功率;|Φ(i,i)|表示IRS 相移矩阵在(i,i)处的元素模值,i∈{1,2,···,L1L2}.优化问题P1为非凸二次规划问题,将公式(14),(15),(16)代入到P1,整理获得优化问题P2:

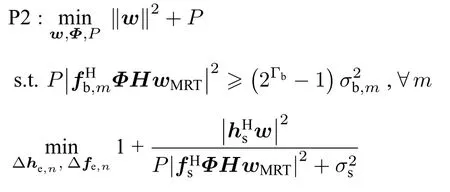
优化问题P3 中的非凸安全可达速率约束C2的不等式右侧可等价表示为[5]

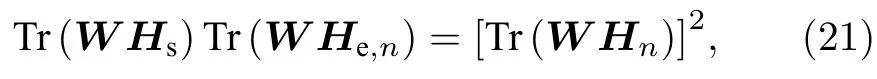
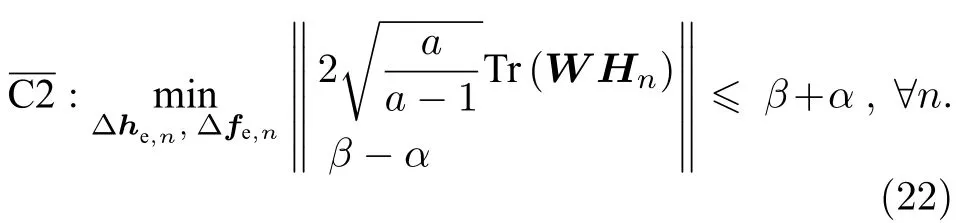
根据公式(24),(25)和(26)所确定的窃听者信道估计误差范数界,可获得

其中,βmax和βmin表示为

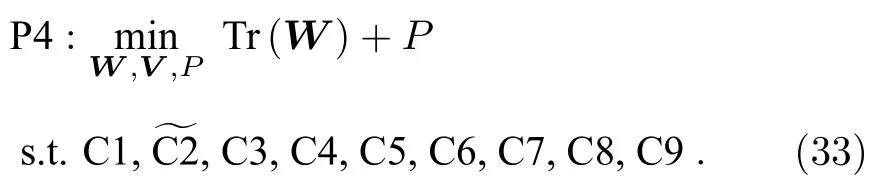
对于优化问题P4,可使用半正定松弛(semidefinite relaxation,SDR)的方法直接消除非凸秩1 约束C6和C8,使之成为一个凸优化问题,此时可利用标准软件工具包进行求解.然而一般情况下,该松弛问题的求解结果无法保证满足秩1 约束,即求解出可能是原优化问题的次优解.针对此问题,本文采用了一种利用惩罚函数的算法,对优化问题P4 进行改写获得优化问题P5:

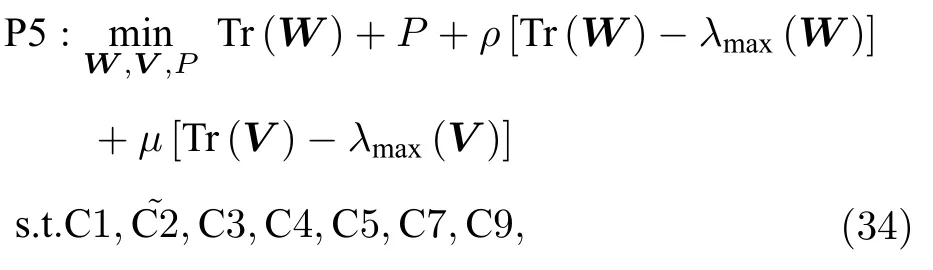
其中,ρ和μ为大于0 的惩罚因子.需要指出的是,对于任意半正定矩阵V而言,Tr(V)-λmax(V)≥0恒成立,故目标函数添加项均为正数.显然,当惩罚因子足够大时优化问题P5 的最优解可逼近优化问题P4 的最优解.对λmax(X)求次梯度∂λmax(X)由λmax(X) 在W处对X的一阶泰勒展开式可以得到

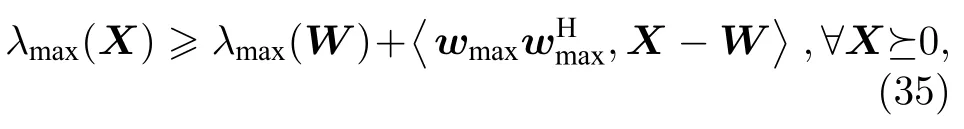
其中,wmax为W最大特征值对应特征向量.利用公式(35)对P5 的目标函数中的λmax(W) 和λmax(V)进行松弛,构建凸优化问题P6:

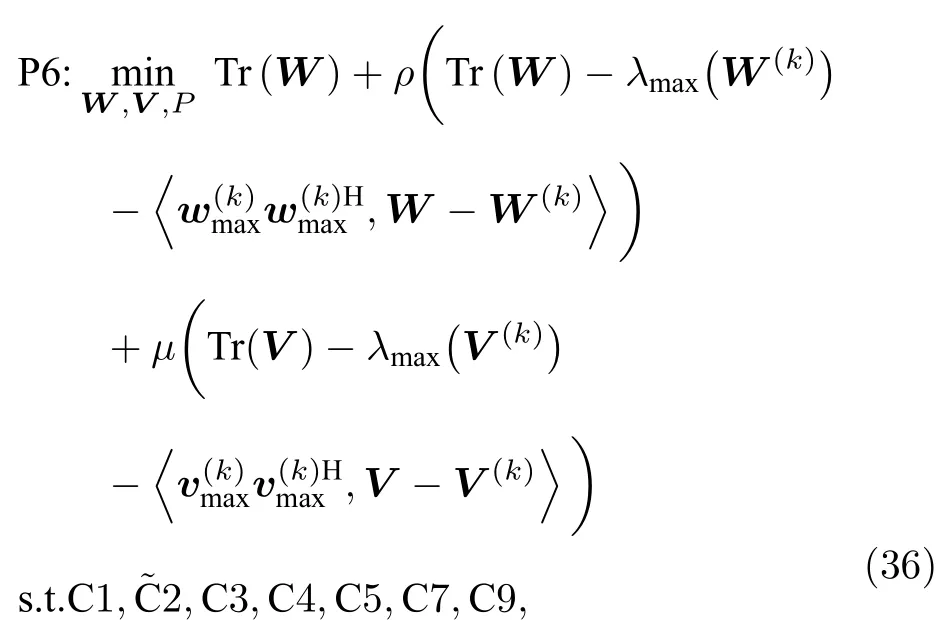
其中,W(k)和V(k)为P6 第k次迭代获得的最优解,具体算法流程如表1 所示.

表1 联合优化算法流程Table 1.Joint optimization algorithm.

4 计算机仿真与分析

本节通过仿真分析评估所提方案的性能.采用2 种基准方案与本文所提方案进行对比,区别分别在于:1)基站不使用IRS 辅助通信;2)基站使用IRS 辅助通信,但其相移矩阵中元素相位随机生成.本文采用地球静止轨道卫星,其高度约为35786 km,假设卫星配备的天线数为K=7,基站配备的天线数为D=7,地面用户和窃听者数为2 个,无人机高度为300 m,以无人机在地面的投影为原点建立直角坐标系,则地面用户的坐标为[20,10]和[50,100],窃听者的坐标为[100,—120]和[—100,—180],地球站的坐标为[—180,100],基站的坐标为[400,0](单位:m);以卫星在地面的投影为原点建立直角坐标系,则无人机的地面投影坐标为[—20,10](单位:km).为简化表达,本节假设窃听者信道误差的范数界为δs,nδnδ.

图2 描绘了δ0.1,ΓbΓs2 bit/s/Hz 时,采用6×6 规模IRS 的归一化3D 辐射方向图及其2D 平面图.从波束辐射图中可以看出,辐射波峰指向地面用户和窃听者并且在地球站位置产生零陷,这说明本文所提算法不仅增强了基站用户的接收信号强度,而且保证了卫星信号的安全可靠传输,此外还抑制了基站信号对地球站的干扰,从而验证了算法的有效性.

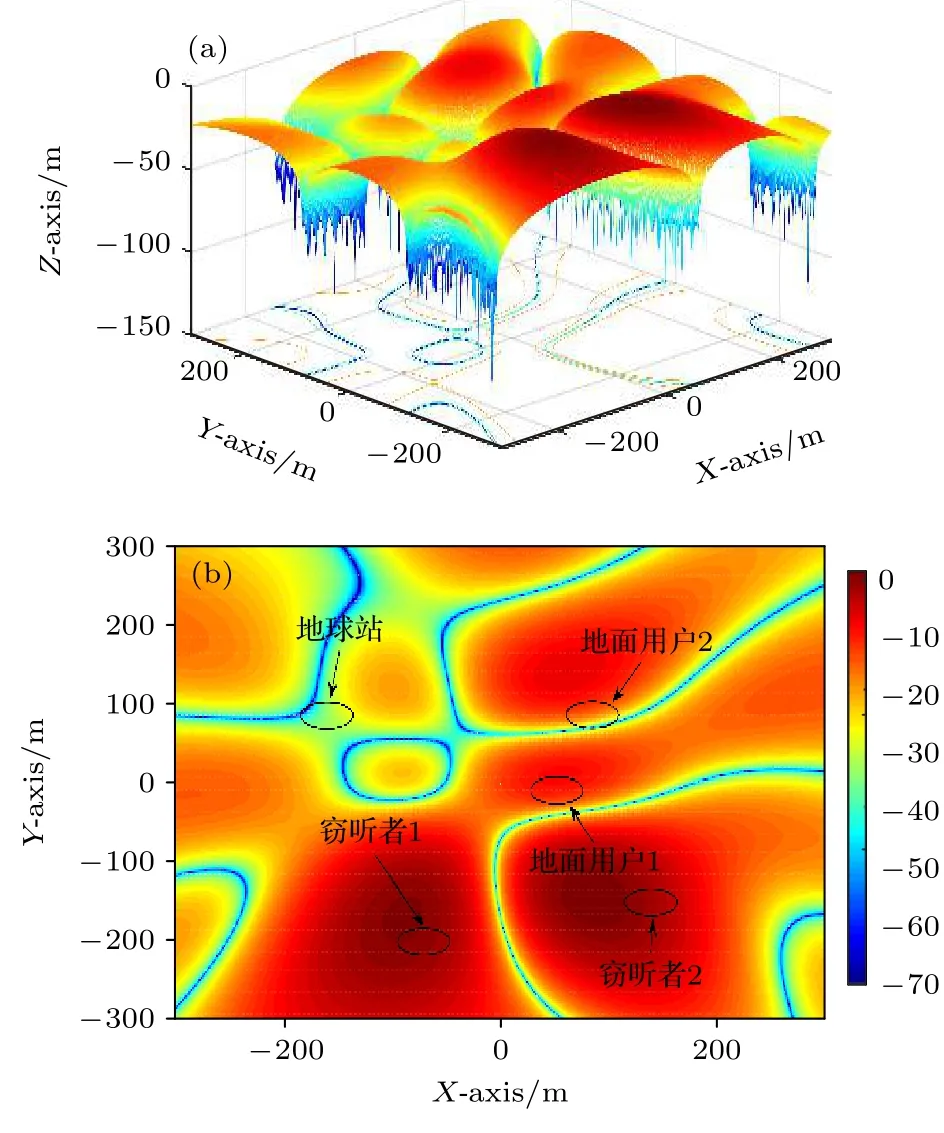
图2 IRS 归一化辐射方向图 (a) 三维图;(b) 二维图Fig.2.IRS normalized radiation pattern:(a) 3D figure;(b) 2D figure.

图3 描绘了采用6×6 规模IRS 时,STIN 总发射功率随安全可达速率Γs变化的性能曲线.从图3中可以看出,随着Γs的增长,STIN 总发射功率也随之提高.这主要是因为Γs的增长将使得地球站接收信号功率要求和友好干扰功率要求提高,从而导致基站和卫星发射功率的提高.此外,本文所提方案始终优于另外两种基准方案.这是因为无IRS辅助方案中基站直接利用BF 技术实现通信和发送友好干扰,缺少IRS 提供的分集增益,致使其总发射功率是三种方案中最高的.而IRS 随机相位方案中,IRS 相移矩阵是从随机生成的样本集中挑选出的,其波束辐射方向难以对准用户,这造成了基站发射功率的浪费,故其总发射功率高于本文所提方案.

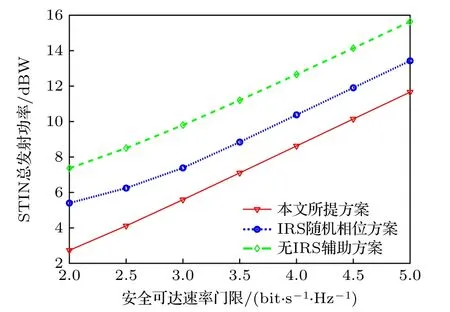
图3 总发射功率与安全可达速率门限的关系Fig.3.Impact of the achievable secrecy rate threshold on total transmitted power.

图4 描绘了本文所提方案中STIN 的总发射功率与Γs,δ的关系.从图4 中可以看出,随着Γs和δ的增长,融合网络总发射功率也随之提高.除上述所提Γs的增长带来的影响外,δ的增长意味着窃听者信道不确定性的提高,即信道的估计误差变大,在进行BF 设计时波束最大增益方向难以完美对准窃听者,导致基站对窃听者的干扰功率降低,此时为了满足系统所需的安全性能要求,基站要进一步提高自身的发射功率.

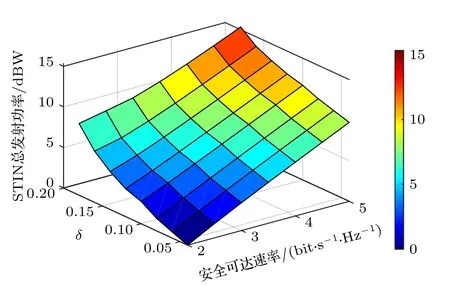
图4 信道估计误差和安全可达速率对系统总传输功率的影响Fig.4.Impact of the channel estimation error and the achievable secrecy rate threshold on total transmitted power.

图5 描绘了Γs3 bit/s/Hz 时,IRS 规模对STIN总发射功率的影响.从图5 中可以看出,在使用IRS辅助的方案中,STIN 总发射功率随着IRS 阵列规模的增大而逐步下降.这主要是因为IRS 为系统提供的自由度和分集增益是与反射元件数成正比的,IRS 规模的增大将使得更多的基站信号功率被反射给用户,从而降低了基站的发射功率.

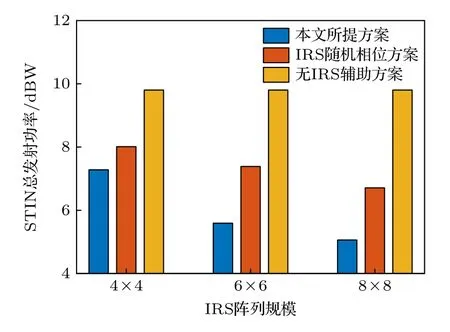
图5 总发射功率与IRS 规模的关系Fig.5.Effect of the IRS size on the total transmitted power.

5 结论

本文在窃听者CSI 非完美的条件下研究了IRS辅助的STIN 通信系统下行安全传输问题.具体而言,就是在在卫星网络无法有效抑制窃听的情况下,基站借助IRS 向窃听者发送绿色干扰,提高卫星通信安全性.在此基础上,建立以系统总发射功率最小化为目标,基站用户服务质量和地球站安全可达速率为约束条件的联合优化问题.为了求解该非凸问题,利用三角不等式和Holder 不等式推导出窃听者非完美CSI 条件下的输出SINR 上下界;接下来,进一步提出了基于半正定规划和惩罚函数相结合的鲁棒BF和功率控制联合优化方法,以实现STIN 的安全可靠传输.最后,计算机仿真结果验证了本文所提算法的有效性和优越性.