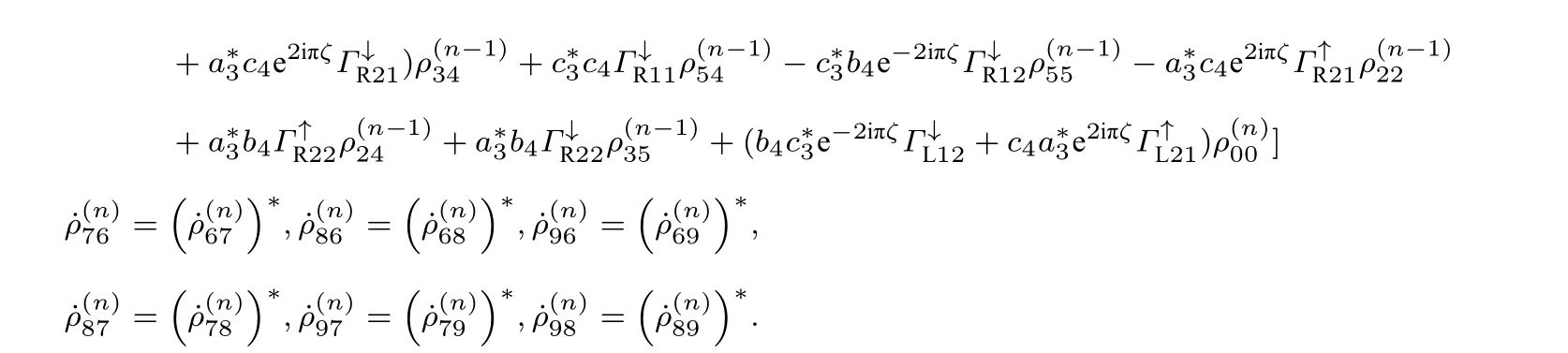自旋轨道耦合量子点系统中的量子相干*

王志梅 王虹 薛乃涛 成高艳

1) (太原师范学院物理系,晋中 030619)

2) (太原师范学院,计算物理与应用物理研究所,晋中 030619)

3) (华中科技大学,武汉国家光电实验中心,武汉 430074)

研究了自旋轨道耦合量子点中的量子相干效应.运用输运电子的全计数统计方法计算系统的平均电流、散粒噪声和偏斜,发现体系存在自旋轨道耦合作用时,散粒噪声值随自旋轨道耦合常数的增加而减小.更重要的是,电流、噪声和偏斜随磁通周期性波动,并且波动周期不受自旋轨道耦合强度大小、自旋极化率以及动力学耦合不对称的影响.

1 引言

量子点是一种通过适当的偏置金属栅极,将电子限制在二维电子气体小区域内的半导体器件.量子点输运[1,2]为观察自旋相关和强相关系统的基本物理现象奠定了基础,如近藤效应[3-5]、库仑效应和自旋阻塞效应[6-8]等.介观纳米结构的量子输运揭示了许多与量子干涉、离散能级和多体关联相关的特性.根据所研究的具体系统,已经发展了一些理论方法,如Landauer-Buttiker 理论和非平衡格林函数方法[9],这两种方法在探究声子非弹性散射和处理多电子库仑相互作用下的介观系统等方面的问题时并不具有广泛性.在某些特定情况下,解决这些问题的一种比较简单的办法是运用率方程方法.然而,这种方法要求偏置电压大、温度为零,这极大地限制了其适用性[10-13].因为量子输运在本质上其实是一个随机的过程,原则上,通过探究相应的分布函数可以充分理解其随机过程,而一阶和二阶累积矩完全足以描述分布函数为高斯分布的一些物理量[14].然而,电流或电导的分布一般来说不是高斯分布.这就需要所有的电流累积量(即全计数统计)包括在内[15-17],以便完全展现出所有阶电荷输运之间的相关性.特别是,由于单个电子隧穿技术高度敏感片上检测技术的发展,所有转移粒子数量的统计累积现在已经可以通过实验进行提取[18].正常态电子的全计数统计已经在理论[19,20]和实验[21-33]中得到了解决.介观系统中电流波动的研究使我们能够获得电子相关信息,而高阶矩能够更全面地描述输运特性.全计数统计可以给定系统所有传输特性的完整信息[34].目前,全计数统计方法已在很多体系中进行了探究,如正常超导体混合结构[35,36]、超导弱链接[37]、隧道结[38]、混沌腔[39]、纠缠电子[40]和自旋相关系统[41]、库仑阻塞系统等.另外,全计数统计的实验测量方案已被提出[42,43].

在两个隧穿的事件之间,量子点态会经历量子相干演化.与隧穿速率相比,快速的相干演化可以很容易地支配系统的整体动力学[44].介观系统是量子相干和退相干极好的探测平台,这是基础物理学和量子器件实现的最重要和最具挑战性的问题之一.Aharonov-Bohm 干涉仪[45,46]是探测相干的标准介观工具,它的振幅是一种很好的相干性量度.介观量子相干之所以重要,是因为它为处理量子自由度的技术开拓了广阔的前景[47].

介观物理学的发展为传输和处理信息的装置中使用电子自旋提供了理论支持.1990 年,Datta和Das 描述了如何运用电场进行调制电流,并展示了场相关的自旋轨道耦合在这一机制中所起的重要作用.Rashba 自旋轨道耦合作用激发了很多的预测、发现和创新概念.通过在空间中移动电子来操控自旋方向,运用自旋方向来控制电子轨迹,发现了一些新的拓扑材料类别.Rashba 自旋轨道耦合作用是由限制势的反演不对称性造成的.二维电子气中的Rashba 耦合强度可以通过改变栅极场实现高达50%的改变[48-52].这一发现再次激发了材料学家和物理学家进一步深入探究反相不对称结构材料的想法.自旋电子学已经是固态物理中的一个重要研究领域,而实验研究方面的进展为介观系统中自旋偏置诱导输运的探究开辟了新的可能性.例如,自旋偏压可以通过控制铁磁和非磁电极偏压接触处的自旋积累来实现[53-55].

自旋极化电流的产生和控制是半导体自旋电子学探究的一个关键课题[56],因此,大量的理论和实验方面的研究都投入在介观系统中,其中最主要的技术之一是自旋注入,它主要依靠光学技术和磁性材料或磁场的使用.然而,光学自旋注入技术很难与电子器件集成,通过铁磁体与非磁性半导体结自旋注入的效率通常很小[57,58],针对这些,最近的一些工作将与自旋相关的输运放置在一些环形或双通道结构.Aharonov-Bohm 环[59]、Stern-Gerlach环[60]、Aharonov-Casher 环[61]、Aharonov-Bohm 干涉仪[62]及双通道半导体器件[63],这些环形导体或双通道器件通常用于研究介观系统中的量子相干效应.Rashba 自旋轨道作用可以避免使用任何磁性材料或场.由于二维电子系统中电场的反演不对称性所产生的Rashba 效应,自旋向上的电子与自旋向下的电子在通过上臂和下臂时会获得不同的相位,从而产生有趣的与自旋相关的相干现象.

目前,关于自旋轨道耦合诱导的量子相干相关方面的研究尚少,本文将运用量子主方程方法重点研究自旋轨道耦合量子点系统中的量子相干效应.

2 理论模型与方法

2.1 理论模型

考虑自旋轨道耦合的量子点系统,其哈密顿量可写为

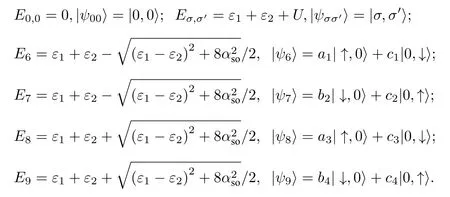
归一化系数

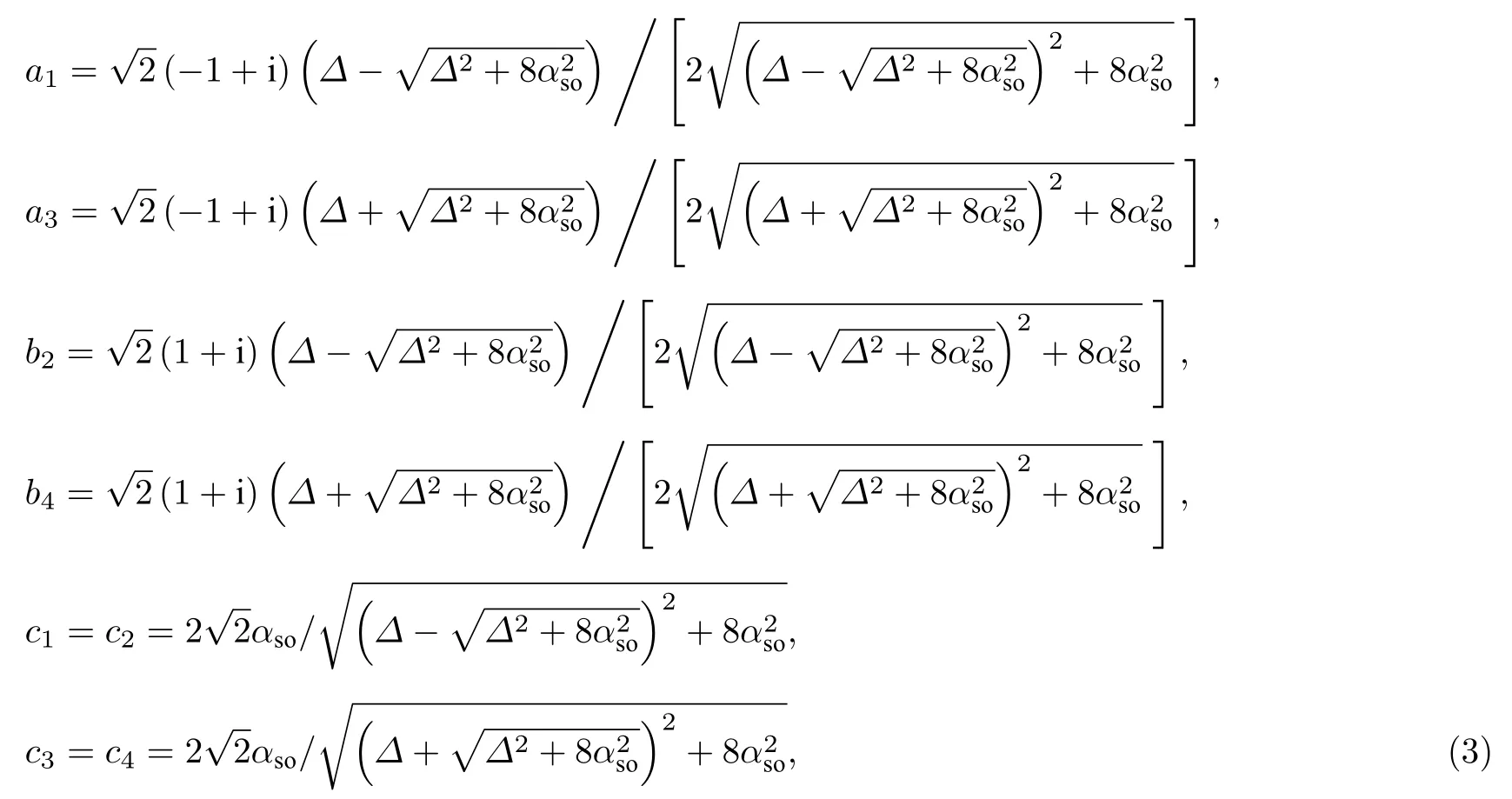
其中Δε1-ε2为能级差.以上述的9 个本征态为基矢,可以获得量子点系统主方程的矩阵元(见附录).

2.2 量子主方程方法

将电极与量子点之间的弱耦合哈密顿量HT作为微扰,系统的量子主方程为

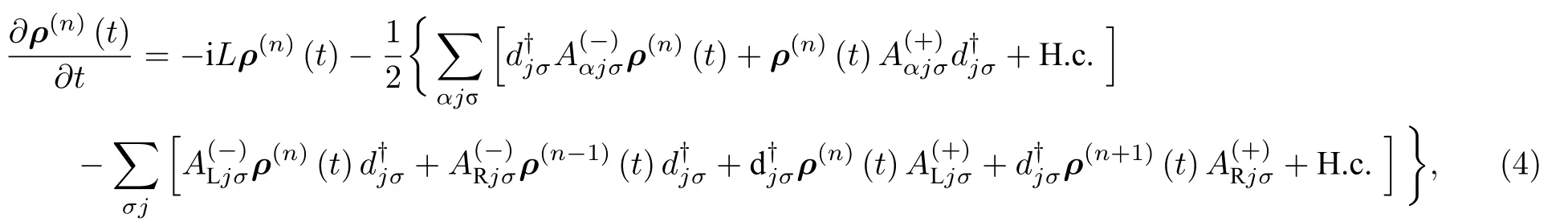
粒子数分辨的量子主方程(4)可表示为

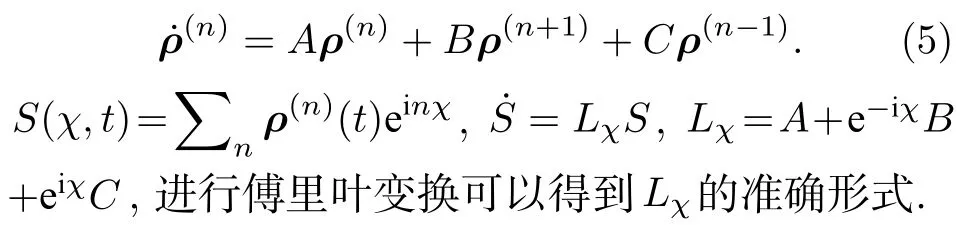
在低频限制下,F(χ)-λ(χ)t,λ(χ) 是Lχ的本征值,而且当χ→0,λ(χ)→0,这样,经过一系列的推导可获得

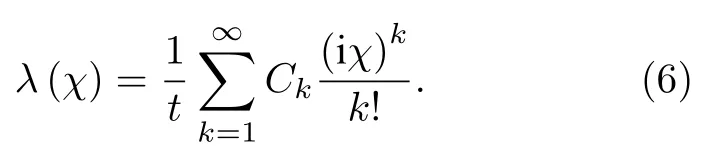
将方程(6)代入久期方程|Lχ-λ(χ)I|0,然后将 (iχ)k展开获得第k阶累积矩

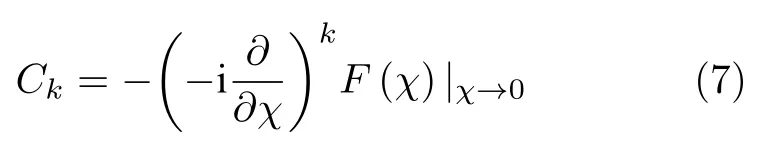
平均电流〈I〉eC1/t与第一阶累积矩有关,散粒噪声 2e2C2/t和第二阶累积矩有关,偏斜与第三阶累积矩C3有关,描述分布的不对称性[64].

通常情况下,散粒噪声可以用FaC2/C1来描述,Fa＞1对应的是超泊松散粒噪声,而Fa＜1 对应的则是次泊松散粒噪声.偏斜度用SkC3/C1表示.

本文以系统的9 个本征态为基矢,运用量子主方程的方法求解电流、散粒噪声和偏斜,考虑量子点体系的非对角元项,可获得一个 33×33 的矩阵,具体的矩阵元表达式见附录.

3 结果分析与讨论

本文运用全计数统计的方法探索自旋轨道耦合量子点系统中的量子相干效应.因为量子点密度矩阵元的表达式比较复杂,无法直接给出累积矩的表达式,本文将给出数值化的结果分析.全文提到的所有量的单位都是meV.

平均电流〈I〉,散粒噪声Fa以及偏斜Sk运用全计数统计的方法可以获得.磁通数ζ反映在非对角元上,两体相互作用与非对角元密切相关[65,66].从系统哈密顿量可知自旋轨道耦合项连接了两体作用,进而可以诱导量子相干.

从图1 可以看到,平均电流〈I〉(图1(a)),散粒噪声Fa(图1(b))和偏斜Sk(图1(c))随磁通ζ周期性波动,振荡周期为0.5.黑色实线、红色虚线和蓝色点线分别为不同自旋轨道作用(αSO0.3,0.6,0.9)下电流,噪声和偏斜的波动图.从图1(a)和图1(b)可以看到,αSO0.3时,电流波动图的峰值为〈I〉0.74,噪声波动图的峰值为Fa3.17;αSO0.6 时,电流波动图的峰值为〈I〉0.81,噪声峰值为Fa2.56;αSO0.9时,电流波动图的峰值为〈I〉0.87,噪声峰值为Fa2.08 .很明显,随着自旋轨道耦合常数的增加,电流在增大,而散粒噪声的值在减小.这是由自旋轨道耦合作用诱导的自旋反演引起的.自旋轨道耦合为电子的隧穿提供了一个新路径.隧穿进发射电极的电子隧穿出量子点到达收集电极将改变它的自旋极化,而且根据隧穿率公式ΓL↑(↓)ΓL(1±p)及ΓR↑(↓)ΓR(1±p) 可以看出,自旋向上的电子隧穿比自旋向下的电子隧穿快,由于这种隧穿的不平衡,散粒噪声值将减小[3].散粒噪声和偏斜的波谷值随自旋轨道耦合强度的增加有下降的趋势,这是由动力学自旋阻塞引起的.但是,可以发现自旋轨道耦合常数的大小并不影响振荡周期.另外,从图1(c)可以看到偏斜Sk的值是从负值变到正值.

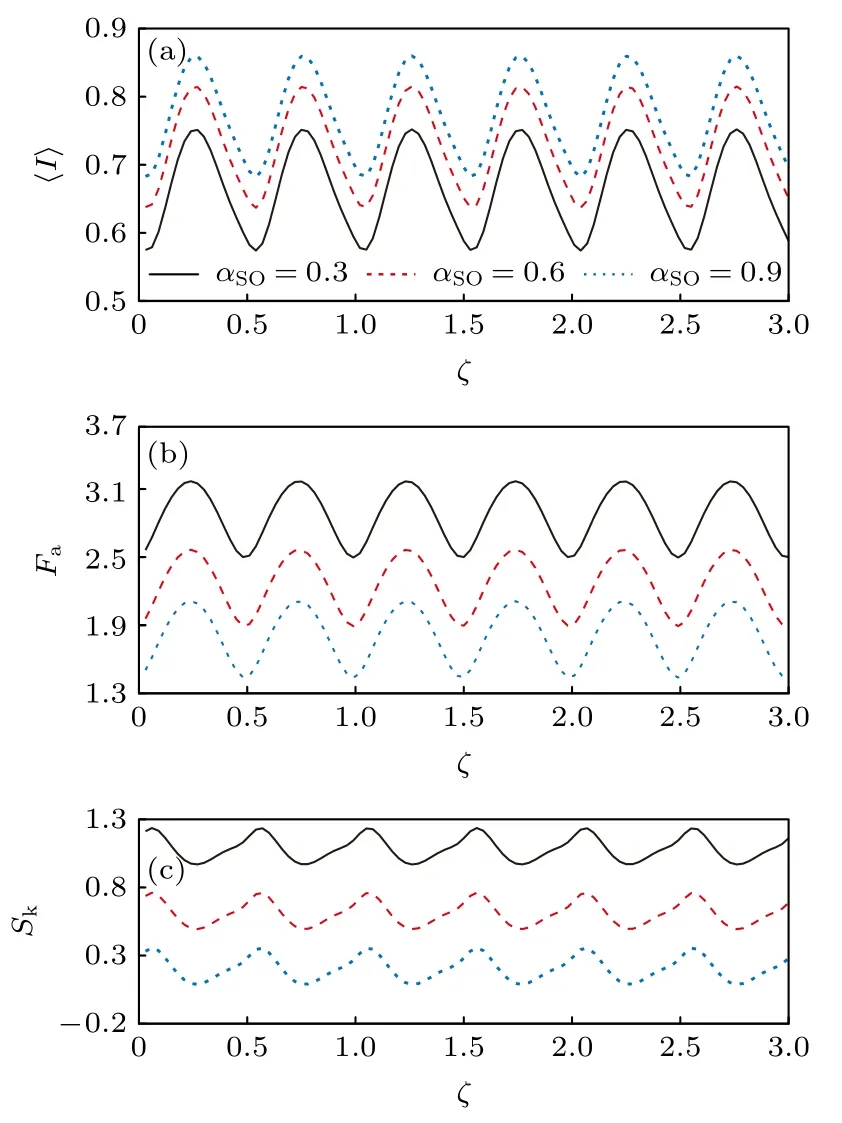
图1 自旋轨道耦合常数αSO不同时,(a)平均电流 〈I〉,(b)散粒噪声 Fa和(c)偏斜 Sk随磁通 ζ振荡图.ε1=1,ε2=3,ΓL=ΓR=0.01,p=0.1Fig.1.(a) Average current 〈I〉,(b) shot noise Fa and (c)skewness Sk fluctuation diagram in different spin-orbit coupling strength αSO .ε1=1,ε2=3,ΓL=ΓR=0.01,p=0.1.

图2 描述的是非对称动力耦合中的量子相干.黑色实线、红色虚线和蓝色点线分别为ΓRΓL,ΓR0.6ΓL和ΓL0.6ΓR下电流、噪声和偏斜随磁通ζ的波动图.可以看到,量子点与电极的耦合不对称不影响振荡周期,振荡周期依然为0.5.但是,波动图中一个周期内多了一个小波谷,当ΓR0.6ΓL,新增的噪声波谷值Fa3.32,当ΓL0.6ΓR,新增的噪声波谷值Fa3.43,这是因为ΓR/ΓL的增加可能导致Γ1L ＞Γ2L,Γ1R≫Γ2R,有效的快慢通道被发展产生了聚束效应.另外,从图2(c)可以看到偏斜Sk的值在处会出现一个小波峰.

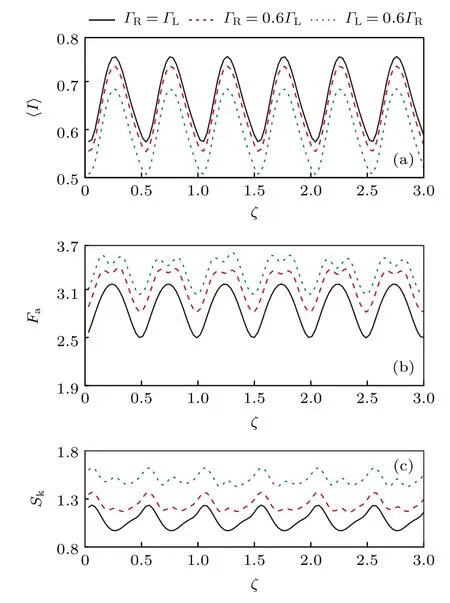
图2 非对称动力耦合下,(a)平均电流 〈I〉,(b)散粒噪声 Fa和(c)偏斜 Sk随磁通 ζ振荡图.ε1=1,ε2=3,αSO=0.3,p=0.1Fig.2.(a) Average current 〈I〉,(b) shot noise Fa and (c)skewness Sk fluctuation diagram for asymmetric dot-electrode coupling.ε1=1,ε2=3,αSO=0.3,p=0.1 .

图3 给出了不同自旋极化率下的量子相干,黑色实线、红色虚线和蓝色点线分别为p0.1,p0.5和p0.9情况下电流、噪声和偏斜随磁通ζ的波动图.振荡周期不随自旋极化率的变化而改变,周期仍然为0.5.但是,很明显,随着自旋极化率p的增大,散粒噪声Fa的值在明显增大,这从图3(b)可以看出,当极化率p0.1,噪声峰值Fa3.17;当极化率p0.5,噪声峰值Fa3.69 ;当极化率p0.9,噪声峰值Fa4.19 .极化率的增大使得自旋向上电子的隧穿率增加,而自旋向下电子的隧穿率减小,这可以根据

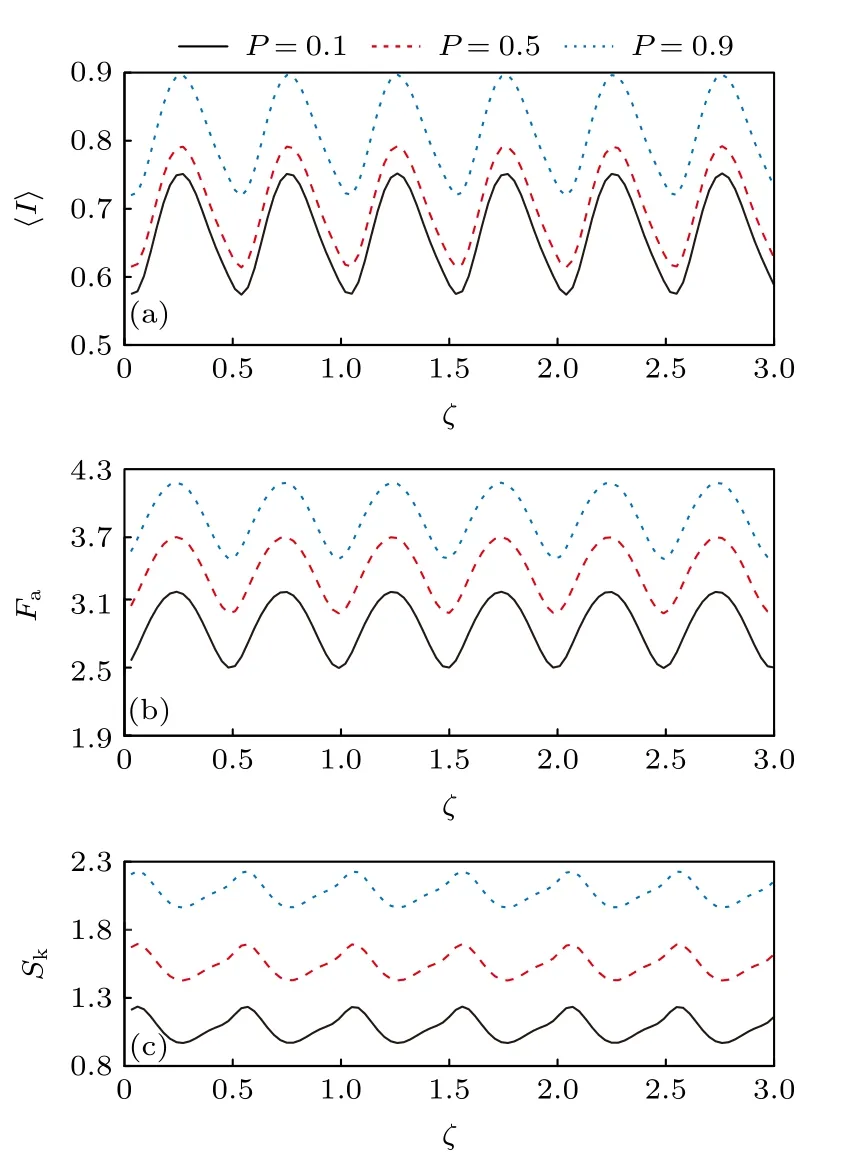
图3 自旋极化率 p 不同时,(a)平均电流 〈I〉,(b)散粒噪声 Fa和(c)偏斜 Sk随磁通 ζ振荡图.ε1=1,ε2=3,αSO=0.3,ΓL=ΓR=0.01Fig.3.(a) Average current 〈I〉,(b) shot noise Fa and (c)skewness Sk with magnetic flux oscillation with different spin polarization p .ε1=1,ε2=3,αSO=0.3,ΓL=ΓR=0.01.

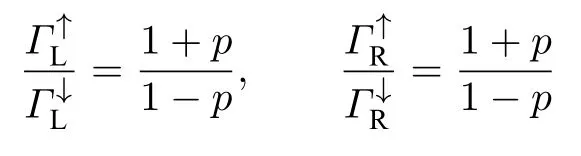
来解释(p ＞0),并且在文献[3]中可以直观地看到隧穿率与自旋极化率的这个关系,这诱导了自旋向上电子与自旋向下电子隧穿过程的竞争,导致自旋聚束效应和明显的超泊松噪声.

4 结论

本文采用量子主方程方法研究了量子点体系中自旋轨道耦合作用引起的量子相干效应.研究发现,当存在自旋轨道作用时,电流、散粒噪声和偏斜随磁通周期性波动.自旋轨道作用诱导量子相干产生,但是自旋轨道耦合的大小不影响振荡周期.此外,动力学耦合不对称和自旋极化率的变化均不影响振荡周期.动力学耦合不对称会使波动图多一个波谷,这与快慢输运通道的竞争有关.而自旋极化率的增加会使波动图的峰值增大,超泊松行为明显,这是因为自旋向上的电子与自旋向下的电子在隧穿过程中竞争而引起的自旋聚束效应.通过测量累积矩可以探索系统中的自旋轨道耦合强度,这将对与自旋有关的器件设计有很重要的科学意义.由于本文主要研究零频累积矩,接下来的工作将主要通过全计数统计方法计算有限频累积矩,这将对整个系统的输运特性有更全面和深入的认识及了解.

附录

系统主方程矩阵元如下.其中对角元项为

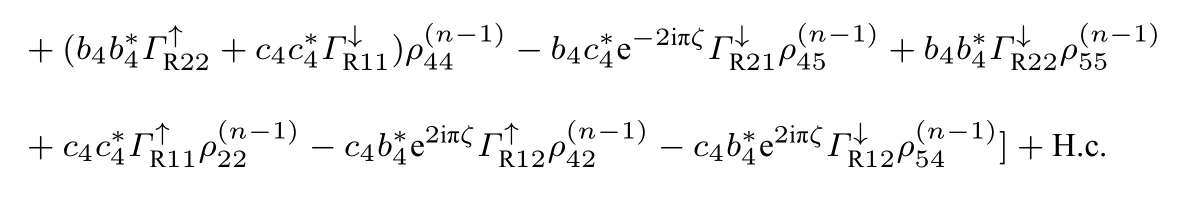
非对角元项为