铝颗粒粉尘对冲火焰数值模拟研究*

张家瑞 夏智勋 方传波 马立坤† 冯运超 Oliver Stein Andreas Kronenburg

1) (国防科技大学空天科学学院,长沙 410073)

2) (清河大楼丁—3,北京 100085)

3) (斯图加特大学,燃烧技术研究所,斯图加特 70569)

铝颗粒由于具有能量密度高、易储存、燃烧过程不产生温室气体等优势,有望成为未来化石燃料替代的解决方案.本文建立了铝颗粒粉尘火焰的燃烧模型,其中考虑了相间传热、相变、表面化学反应、气相详细化学反应及辐射传热等过程,并针对铝颗粒粉尘对冲火焰开展了数值模拟研究.首先,通过仿真McGill 大学的铝颗粒粉尘对冲火焰实验进行模型验证,并分析了实验中使用铝颗粒本身作为示踪粒子引起的气相速度测量误差,结果表明,数值模拟得到的离散相速度分布与实验结果基本一致,火焰传播速度的预测值也同实验数据吻合较好.当颗粒粒径小于10 μm 时,连续介质假设不再成立,相间传热模型必须考虑过度区机制,随着颗粒粒径的增加,火焰传播速度不断降低.随着对冲火焰拉伸率的增加,颗粒在火焰区的停留时间减少,并出现燃烧不完全的现象,粉尘火焰由双峰变为单峰结构.火焰传播速度随着拉伸率的增加而增大,通过线性外推可得到未拉伸的火焰传播速率约为29 cm/s.辐射引起的热损失会导致气相温度大幅降低,但辐射传热对颗粒的加热作用相对较小.

1 引言

金属颗粒因其较高的燃烧温度和能量密度、易储存等优点广泛应用于固体火箭发动机[1]、固体火箭冲压发动机[2,3]、脉冲爆震发动机[4]和粉末燃料冲压发动机[5]等动力系统.在民用领域,由于燃烧过程不产生二氧化碳等温室气体,并且凝相燃烧产物极易回收[6],金属颗粒有望成为一种高能量密度的储能载体,为全球气候问题提供一种解决方案[7].

针对固体颗粒粉尘燃烧过程,前期的研究主要集中于确定其火焰传播速度.从上世纪九十年代至今,国内外学者在不同实验构型上针对铝颗粒粉尘火焰开展了大量的实验研究,包括本生灯火焰[8-13]、对冲火焰[14]及球形自由扩散火焰[15]等.虽然上述文献中采用的颗粒粒径相近,但测得的火焰传播速度却相差较大(从10[12]到30 cm/s[14]).主要原因可能有两个:一是火焰传播速度测量方法不同,例如,在文献[9]中利用粒子图像测速法(particle image velocimetry,PIV)测量了铝颗粒粉尘本生灯火焰的速度场,并将粉尘火焰传播速度定义为垂直于火焰面方向上的最小速度,而在文献[13]中,铝颗粒粉尘本生灯火焰的传播速度被定义为锥形火焰面面积除以总的气体体积流量;二是实验装置中的系统误差,例如,火焰面的褶皱对球形自由扩散装置火焰的火焰传播速度的影响难以准确评估[15].相比之下,对冲火焰实验装置结构简单、系统误差较小、重复性较好[14],更为重要的是,对冲火焰中的火焰传播速度的定义没有争议,即为火焰面上游速度的最小值[16].因此,本文采用McGill 大学的铝颗粒粉尘对冲火焰[14]作为研究铝颗粒粉尘燃烧特性的仿真对象.

近年来,针对铝颗粒粉尘火焰燃烧特性的理论与数值模拟研究逐渐增多.Huang 等[17]采用单个颗粒燃烧时间的经验公式计算颗粒的消耗速率,建立了铝颗粒-空气一维稳态平面火焰传播模型,作者指出火焰传播速度遵循定律,dp为颗粒直径,对于微米颗粒,n=0.92.Bocanegra 等[18]建立了相似的一维火焰理论模型,但关键模型参数的选取是根据实验数据拟合得到.Han和Sung[19]综合考虑了颗粒相变、表面化学反应和辐射传热等过程,在欧拉-拉格朗日框架下研究了一个半开管道内铝颗粒-空气粉尘火焰传播过程,并开展了当量比、颗粒粒径等参数化研究.Zou 等[20]通过考虑不同克努森数下的传热模型,建立了空气中纳米级铝颗粒粉尘火焰燃烧模型,在文献[19]的基础上研究了类似的火焰传播过程,作者将火焰面移动的速度定义为火焰传播速度,而火焰面的位置是由一个点火温度经验关系式决定的[21].上述研究中[18-20]的模型验证均是通过与火焰传播速度的实验数据进行简单而直接的对比,并没有考虑仿真中的火焰拉伸率(strain rate,SR)是否与实验数据中相应的火焰拉伸率保持一致.研究表明,在当量比一定的条件下,火焰拉伸率对火焰传播速度的影响十分显著[16],该结论也在铝颗粒粉尘火焰中得到初步证实[22].此外,针对颗粒燃烧的欧拉-拉格朗日方法在面向固体火箭发动机内流场的仿真中应用较为广泛,Najjar 等[23]考虑了氧化铝帽的生长及氧化铝烟雾的演化过程,重点研究了颗粒尺寸分布对发动机燃烧过程的影响;刘平安等[24]将铝颗粒的表面反应模型应用于含铝复合推进剂发动机内流场的研究中,分析了铝的分布燃烧对固体火箭发动机内流场带来的影响;Li 等[25,26]在欧拉-拉格朗日框架下研究了固体火箭超燃冲压发动机内流场的燃烧过程,并指出颗粒燃烧充分与否是决定发动机燃烧效率的决定性因素.

综上,本文的目的是在欧拉-拉格朗日框架下建立铝颗粒粉尘火焰的燃烧模型,并研究对冲火焰结构中的铝颗粒粉尘火焰燃烧特性.首先,该模型被用于模拟一个实验室尺度的对冲火焰,并通过对比气相速度、离散相速度和火焰传播速度验证其准确性.随后,研究并讨论了相间传热、颗粒粒径、拉伸率和辐射对铝颗粒粉尘火焰的影响.

2 模型的基本方程

2.1 离散相模型

铝颗粒在点火燃烧过程中将经历熔化、表面化学反应及蒸发等复杂的物理化学过程,为了便于求解,假设铝颗粒为均匀球形,并可视为质点,其质量方程如下:

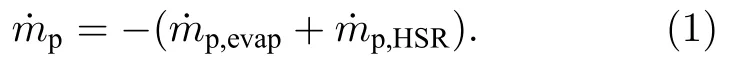
下标p表示离散相颗粒,(1)式右侧两项分别表示由蒸发及表面化学反应引起的颗粒质量变化.

动量方程为

其中Cd为阻力系数[27]:

能量方程为

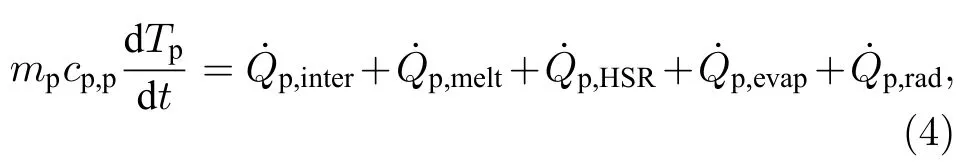
其中T表示温度;cp,p为颗粒比热容;分别表示相间传热、熔化、表面化学反应和蒸发源项,具体封闭形式在下文给出.

颗粒与气相的相间换热速率可以表示为

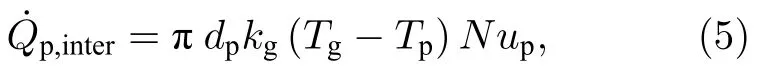
其中kg为导热系数;Nup为颗粒的Nusselt 数,可由Ranz-Marshall 模型[28]得到:

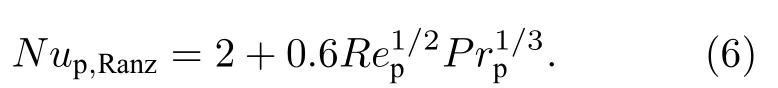
当颗粒尺寸在微米级别时,周围气体的连续介质假设可能不再成立[29],因此引入Kavanau 模型[30]对过渡机制(transition regime)的Nusselt 数进行修正:

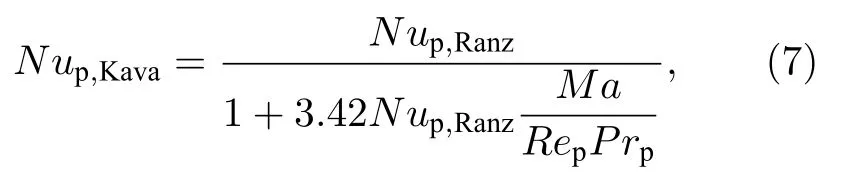
其中Ma为马赫数;Prp为颗粒的Prandtl 数.

当颗粒温度达到铝或氧化铝的熔点,并且相应固态物质的质量分数大于零,则(4)式左侧等于零,此时颗粒的熔化速率可表示为

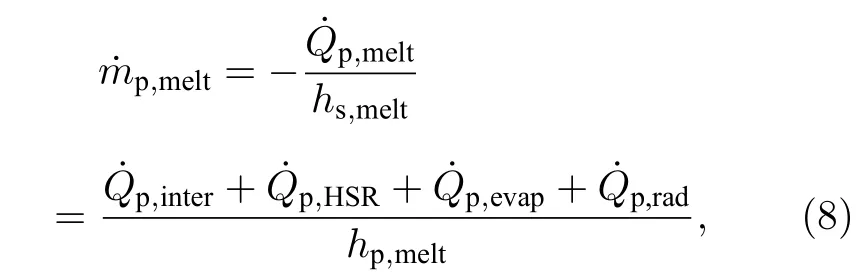
其中hs,melt为熔化潜热[31].固态铝熔化为液态之后,将会与环境中的空气发生表面化学反应,采用一个单步总包反应表示该过程:

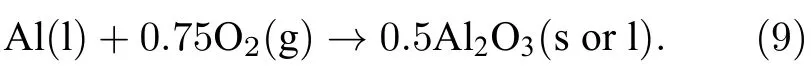
并假设产物氧化铝(Al2O3)全部沉积在颗粒表面,铝的反应速率表示为[32]

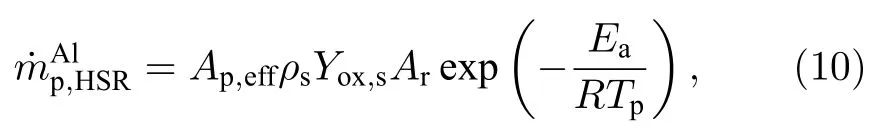
其中Ap,eff表示颗粒中液态铝的等效表面积[19];ρs表示颗粒表面的气体密度;Yox,s表示颗粒表面的氧气质量分数.指前因子Ar1.5×104m/s,反应活化能Ea83.72 kJ/mol .颗粒能量方程,即(4)式,中的源项可计算为

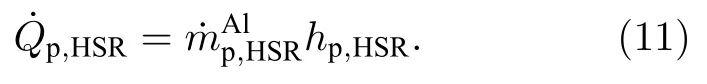
hp,HSR为(9)式所示的表面化学反应的反应热.液态铝的蒸发过程可采用Spalding 模型描述:

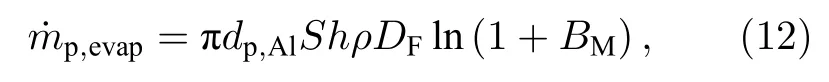
其中dp,Al为液态铝的等效直径[19];Sh为颗粒的Sherwood 数,假设Lewis 数为1,颗粒的Sherwood数与Nusselt 数相等;DF为气态铝的扩散系数[33];BM为传递系数:

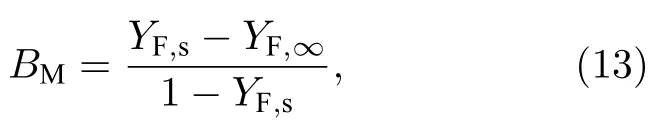
其中YF,s和YF,∞表示颗粒表面与气相环境中的气态铝的质量分数,颗粒表面铝蒸气的质量分数为

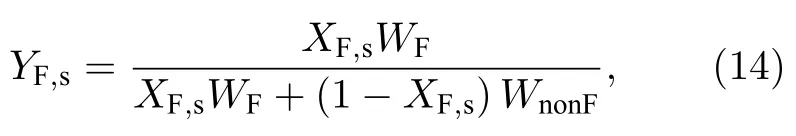
其中X表示摩尔分数;W表示相对分子/原子质量,下标F 与nonF 分别表示燃料蒸气与非燃料蒸气混合物.假设颗粒表面的铝蒸气和液滴处于气液平衡,则表面蒸气的摩尔分数可计算为

其中PF,sat为铝蒸气的饱和蒸汽压;Pa为环境压力.颗粒能量方程,即(4)式中的源项可计算为

其中hp,evap为蒸发潜热.

2.2 连续相模型

本文研究的是层流条件下铝颗粒粉尘火焰燃烧过程,连续相的控制方程可以表示为

其中ρ为密度;uj表示j方向上的速度分量,μ为动力性黏性;h为气相的焓;Yk表示第k种组分的质量分数;分别表示气相与离散相产生的质量、动量和能量交换.表示化学反应产生的源项.

本文采用了文献[17]提供的铝-空气详细化学反应机理,如表1 所列,包括8 种组分和10 步反应,由于Al2O3难以气相形式稳定存在,本文采用一个活化能为零的不可逆反应,如表1 中反应11所示,描述气相氧化铝凝结为凝相氧化铝[Al2O3(l)]的过程[33].由于凝相氧化铝是以纳米级的烟雾形式存在[6],本文沿用文献[17,33]中的处理方法,将凝相氧化铝视为连续相的一部分.

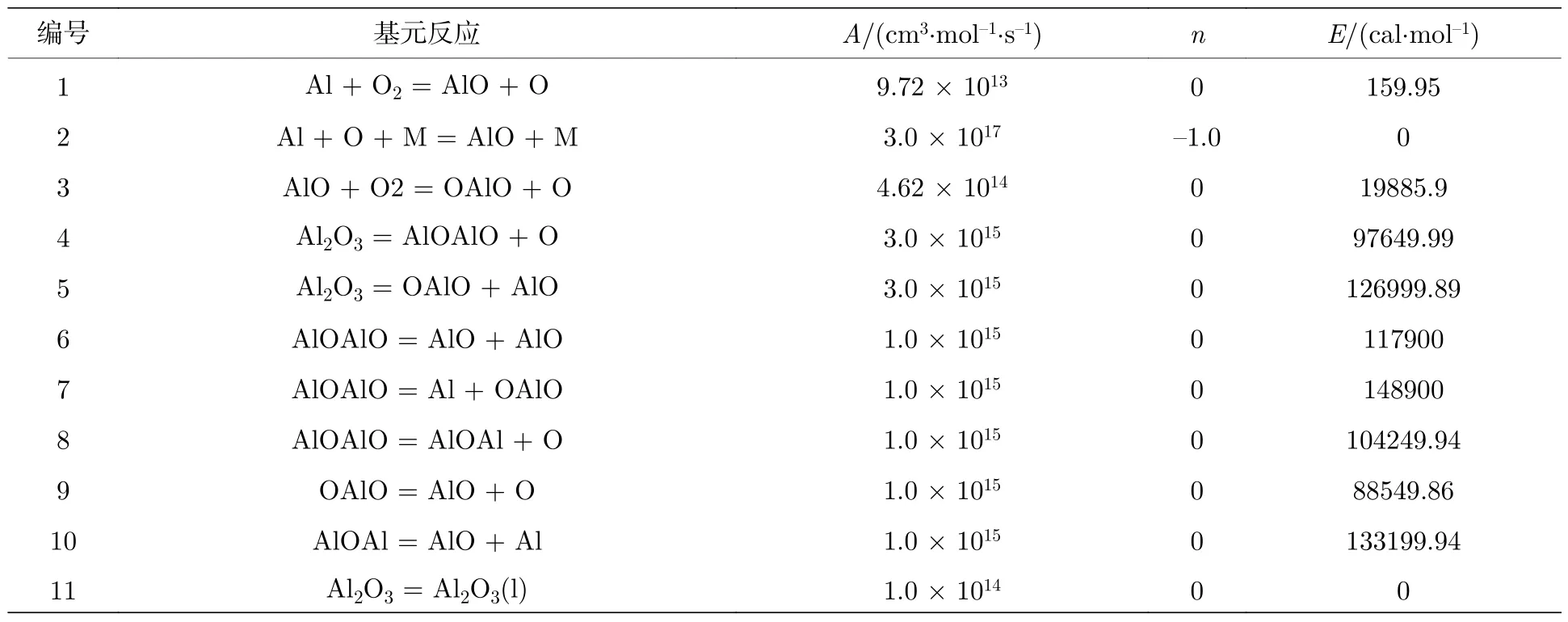
表1 铝-空气详细化学反应机理Table 1.Al/O2 gas-phase mechanism.

铝颗粒粉尘火焰燃烧过程中会伴随强烈的辐射换热,颗粒能量方程[(4)式]和气相能量方程[(19)式]中的辐射源项可计算为

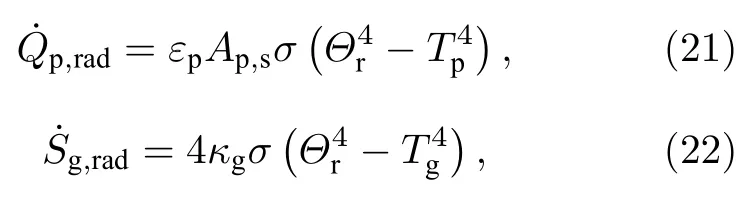
其中εp0.12为颗粒的发射率[34];Ap,s为颗粒的投影面积;σ为Stefan-Boltzmann 常数;κg为气相的吸收系数,由于凝相氧化铝的发射率远高于其他气体,气相的吸收系数可近似为

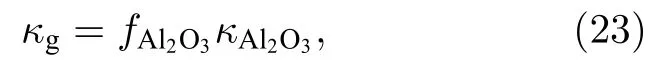
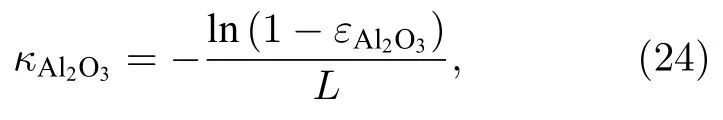
其中Vd为计算域的体积;Ad为计算域的表面积.(21)式与(22)式中的Θr为连续相的辐射温度:

其中G为入射辐射,采用离散坐标法求解辐射传输方程[35]得到入射辐射G从而完成辐射传热模型的封闭.

3 算例设置与数值方法

本文的仿真对象为文献[14]所测量的一个层流铝颗粒粉尘对冲火焰,以下简称为目标火焰,为了节约计算资源,将计算域简化为如图1 所示的二维结构,其中铝颗粒-空气混合物从底部燃料端以均匀的速度向上注入计算域,纯空气由顶部氧化剂端以相同的速度向下注入计算域,若无特殊说明,底部与顶部入口速度的大小均为1.8 m/s,与目标火焰保持一致.计算域的长度和宽度等于文献中的喷嘴间距(20 mm)和喷嘴直径(15 mm).燃料端的铝颗粒及空气和氧化剂端的空气初始温度均为300 K,左右两侧为出口边界条件.

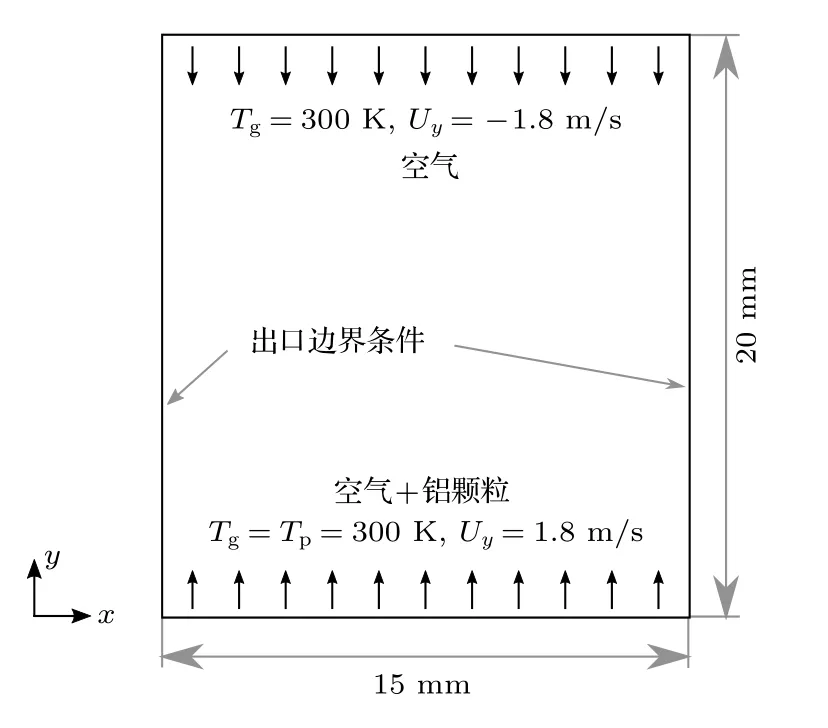
图1 铝颗粒粉尘对冲火焰的计算域和边界条件Fig.1.Computational domain and boundary conditions for the counterflow flame with aluminum particles.

为了得到稳定的铝颗粒粉尘对冲火焰,首先对图1 所示的冷态铝颗粒粉尘进行0.02 s 的仿真,随后在计算域中部设置一块3000 K 的高温区域用于点火,再经过0.02 s 的计算即可得到稳定的铝颗粒粉尘对冲火焰.后续计算结果中的气相参数,如温度、组分浓度及速度等均为火焰稳定后0.04 s 内的平均值.

为了研究二维算例的合理性及计算结果对网格分辨率和时间步长的敏感性,设置了6 个算例,如表2 所列.图2 展示了6 个算中气相温度及氧气浓度在对冲火焰轴线上的分布,其中仿真采用了与文献[14]中相同的铝颗粒粒径分布和相同的铝颗粒浓度(400 g/m3).通过对比Case 1和Case 2 的结果,发现二维算例得到的火焰温度和组分分布与三维算例较为接近,但三维算例所需的计算时间约为9200 核时,是二维算例的37 倍.综合考虑计算精度与计算成本,本文的数值仿真工作均在二维网格上展开.通过比较Case 2,Case 3和Case 4 的结果可以发现,当网格分辨率增大到125 μm 时,计算结果对网格分辨率的敏感性极低.此外,通过比较Case 2,Case 5和Case 6 的结果可以看出,仿真对于时间步长的依赖性极弱.因此,本文将图1所示的二维计算域离散为120×160 个网格,网格分辨率为125 μm,时间步长固定为1×10—6s.

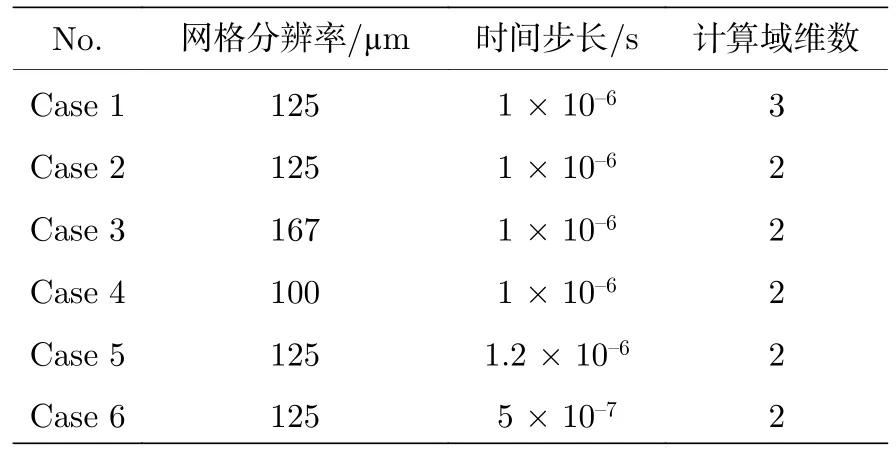
表2 网格分辨率及时间步长敏感性分析算例Table 2.Case setups for mesh resolution and time step sensitivity investigations.

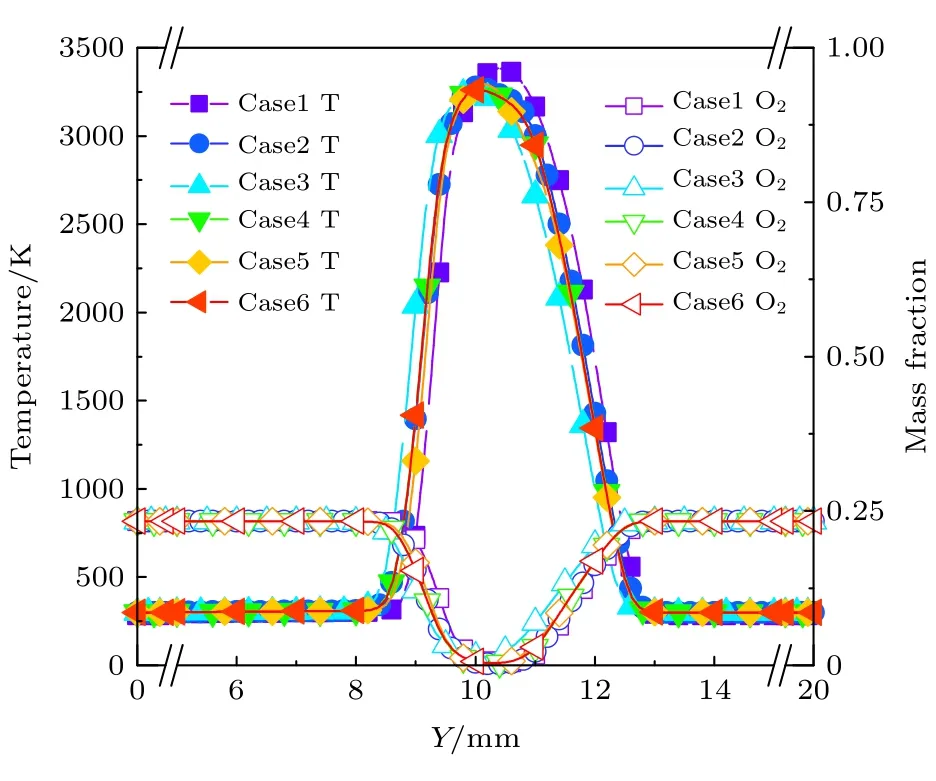
图2 不同网格分辨率/时间步长下的铝颗粒粉尘对冲火焰轴向参数分布Fig.2.Average axial profiles across the aluminum counterflow flame under different mesh resolutions and time steps.

本文采用的求解器是在开源计算流体力学库OpenFOAM 基础上开发的,速度和压力的耦合适用PIMPLE 算法求解.对于气相控制方程,时间项使用二阶隐式格式,动量方程中的对流项采用线性迎风格式,标量方程中的对流项和所有扩散项采用中心差分格式.

4 结果与讨论

在3.1 小节的模型验证中,采用了与目标火焰中相同的铝颗粒粒径分布和相同的铝颗粒浓度(400 g/m3).为了更好地控制变量并研究颗粒粒径对火焰的影响,在3.2 小节及之后的数值仿真中采用的铝颗粒为单一均匀粒径,并且,为了突出不同工况下火焰结构的区别,底部入口处的铝颗粒浓度均为500 g/m3,对应的当量比约为1.5.

4.1 模型验证

4.1.1 速度场文献[14]采用PIV 方法测量了目标火焰的速度场,其中流场中的铝颗粒被当作示踪粒子,图3对比了本文计算的离散相与气相速度场与相应实验数据,图中下标Sim.表示本文的计算值,Exp.表示文献中的测量值,从图中可以看出本模型预测的离散相速度与实验数据非常吻合,但是气相速度场存在一定误差,具体原因将在下文分析.

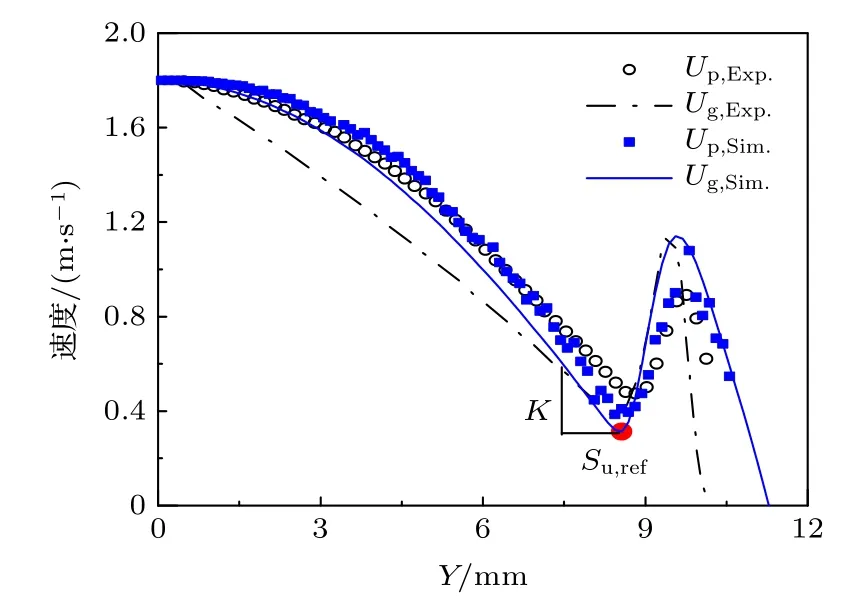
图3 目标火焰中离散相与气相速度场的计算值与实验测量值的对比Fig.3.Comparison of the velocity profiles of both particles and gas phase of the target aluminum opposed jet flame calculated in the present study and experimental data.

由于目标火焰中的铝颗粒的粒径分布范围较广(1—15 μm),索特平均粒径为5.6 μm,随流性较差,文献[14]采用下式计算气相速度:

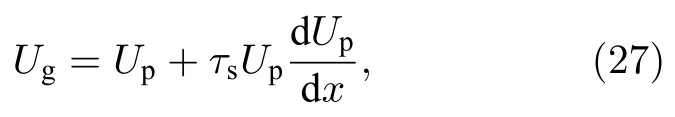
其中Ug为估算的气相速度值;Up为PIV 方法直接测量得到的离散相速度值;τs为颗粒的Stokes 时间.为了确定目标铝颗粒的τs,文献[14]先后利用目标铝颗粒与随流性极好的氧化铝粒子作为示踪粒子(近似认为氧化铝粒子速度等于气相速度),测量了同一个冷态对冲射流(无燃烧)的速度场.将所测得的速度分布带入(27)式,从而得到目标铝颗粒的等效τs约为1 ms.为了研究τs对气相速度场计算的影响,模拟了两个冷态对冲射流,每个工况中的颗粒粒径都是均匀的,分别等于5.6 μm 与15 μm,速度分布预测结果如图4 所示,其中下标Sim.表示本文的计算值,Ug,Est表示由离散相速度根据(27)式及相应τs估算的气相速度.从图4 中可以看出,(27)式可以根据离散相速度较好地计算出气相速度,特别是对于小粒径颗粒[图4(a)],但是其关键在于选择恰当的τs.过小的τs会导致气相速度被高估,反之则会低估.此外,通过对比图4(a)与图4(b)可以发现,不同粒径的颗粒对应不同的最优τs值,并且最优的τs值相差较大.因此,利用(27)式根据粒径分布较分散的颗粒计算出的气相速度可能存在较大误差,所以直接对比图3 中离散相的速度分布进行模型验证更为可靠.

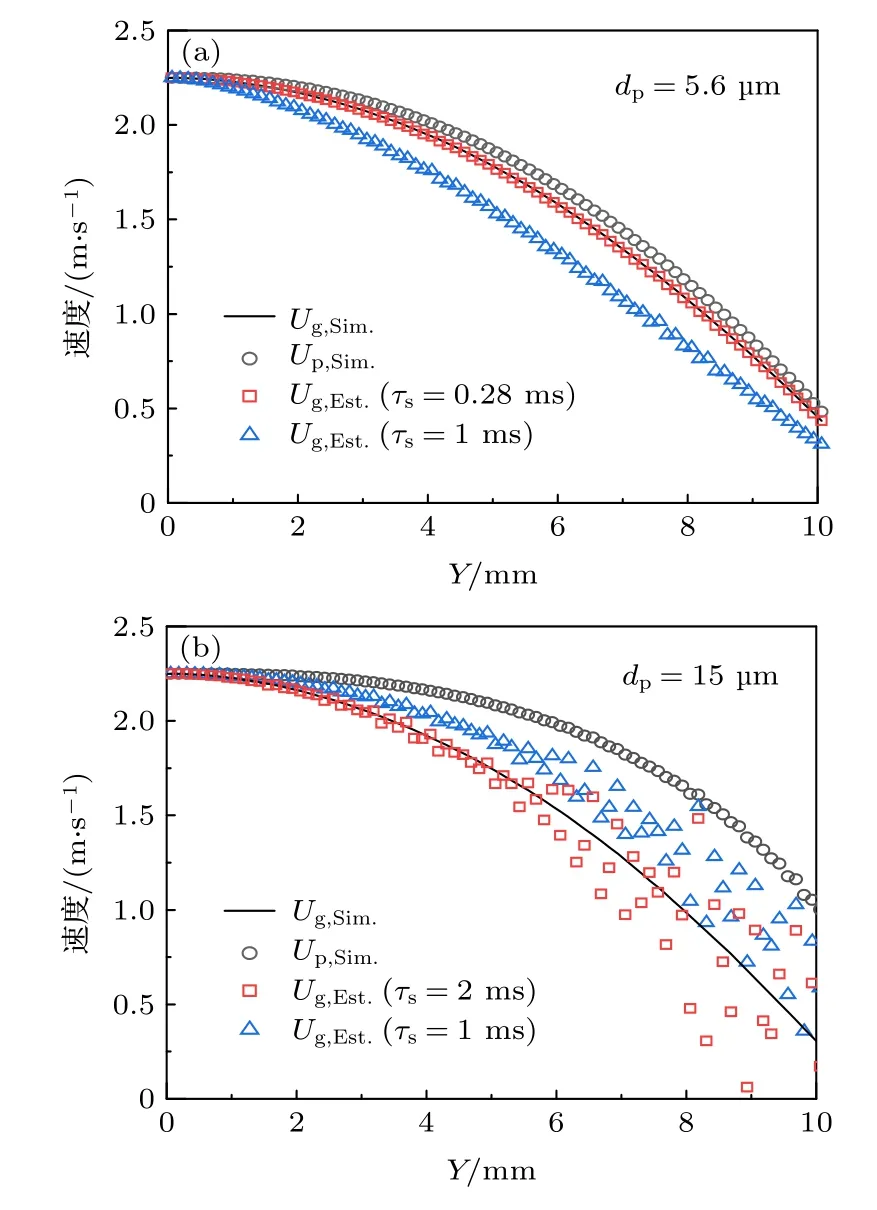
图4 冷态对冲射流的气相与离散相速度分布 (a) dp=5.6 μm;(b) dp=15 μmFig.4.Velocity profiles of gas phase and particles in non-reacting counterflow:(a) dp=5.6 μm;(b) dp=15 μm.

4.1.2 火焰传播速度

根据文献[14],铝颗粒粉尘对冲火焰的火焰传播速度定义为火焰上游气相速度的最小值,提取了气相速度沿对冲火焰轴线的分布,并根据该定义得到火焰传播速度,如图3 中Su,ref所示.此外,文献[14]引入了局部拉伸率K(如图3 所示)以确保不同铝颗粒浓度下的对冲火焰的拉伸率保持不变,本小结的数值仿真也满足该约束.图5 对比了本研究计算的火焰传播速度与文献中的实验数据,总体而言,预测的火焰速度与实验结果基本一致,并且与粉尘浓度无显著相关性,验证了本文模型的准确性.这种无显著相关性的主要原因是,离散项颗粒所占体积可以忽略,因此增加颗粒浓度虽然导致气固混合物的比热比的增大,但不会显著影响颗粒当地的氧气浓度,所以颗粒的表面化学反应速率保持在一定水平;此外,由于颗粒浓度的增加,单位体积内的颗粒表面积增加,一定程度上增大了颗粒群的整体反应及蒸发速率,弥补了由于当量比的增加导致的火焰温度降低的负面效果.

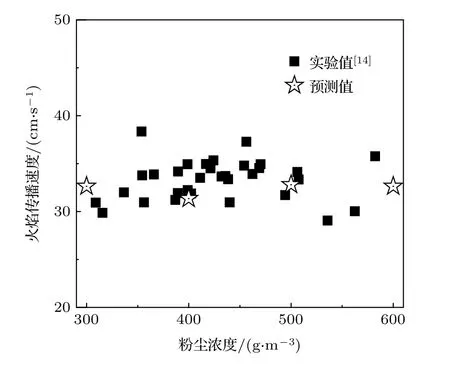
图5 不同粉尘浓度下火焰传播速度的预测值与实验值[14]的对比Fig.5.Comparison of the flame speed calculated in the present study and the experiments in Ref.[14].

4.2 火焰结构分析

图6 所示为铝颗粒粉尘对冲火焰的平均气相温度(左)与AlO 分布(右)云图,其中铝颗粒的颜色分别表示其温度(左)与液态铝含量(右).反应区(AlO 所在区域)稳定在两个喷嘴之间,火焰的最高温度接近3400 K.在相间传热和表面化学反应的作用下,颗粒进入反应区后温度迅速升高,如图6(左)所示.熔化后,颗粒内部的所有固态铝都熔化为液态并开始蒸发,见图6(右).从右侧绿色圆圈中可以看出,经过高温反应区后,颗粒中液态铝的质量分数再次下降到接近于零,表明大部分液态铝已经被蒸发为气态,或者被表面化学反应所消耗.

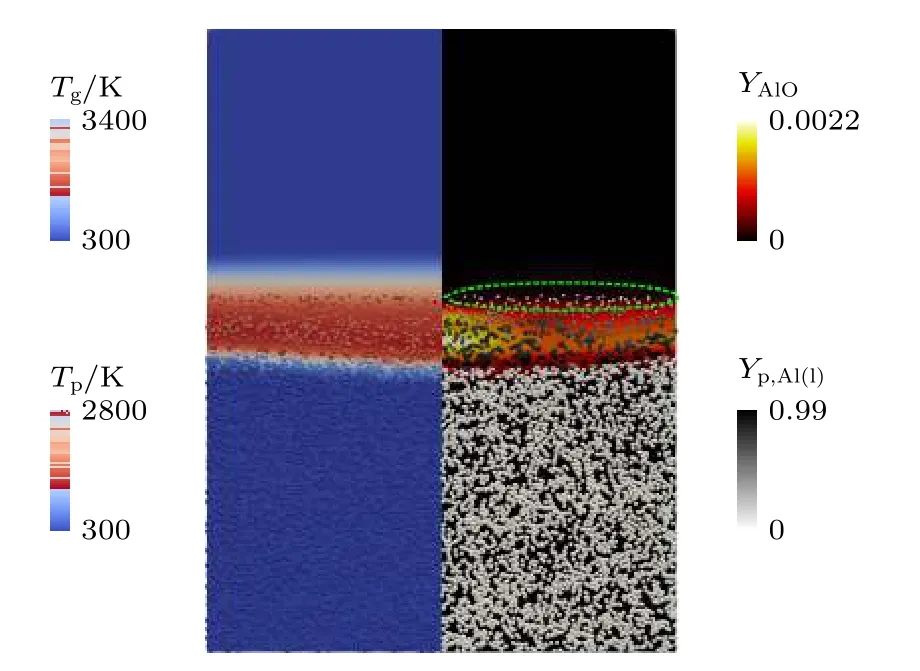
图6 对冲火焰的时均气相温度(左)和AlO 分布(右)和铝颗粒粉尘分布.颗粒浓度:500 g/m3,颗粒直径:5.6 μmFig.6.Time-averaged gas temperature (left) and AlO mass fraction fields (right) and instantaneous particle clouds.Dust concentration:500 g/m3,particle diameter:5.6 μm.

图7 所示为图6 中的对冲火焰主要参数沿轴向的分部.图7 中蓝色虚线表示速度为零的滞止面,火焰区定义为氧气的消耗超过1%的区域.在0＜Y＜ 8.5 mm 的区域内,气相温度与氧气含量保持不变,表明该区域内没有发生显著的物理或者化学过程;在8.5 mm＜Y＜ 12.8 mm 的区域内,铝-空气反应的中间产物AlO 在下侧(左侧)边界生成,表明铝-空气气相化学反应的开始,并且此处气相温度显著升高.由于该工况下的颗粒浓度为500 g/m3,对应的化学当量比约为1.5,所以由底部(左侧)注入空气中的氧气被完全消耗,剩余的气态铝及亚氧化物需要氧化剂端(右侧)注入的空气进一步氧化.在滞止面(Y=11.5 mm)附近,气态铝和AlO 的质量分数减小至零,说明在滞止面上侧(右侧)几乎没有气相反应发生,因此,气体温度在滞止面附近快速降低.最终燃烧产物凝相Al2O3(l)同AlO 一起在火焰区上游生成,并且在扩散作用下分布在一个更宽的范围内.

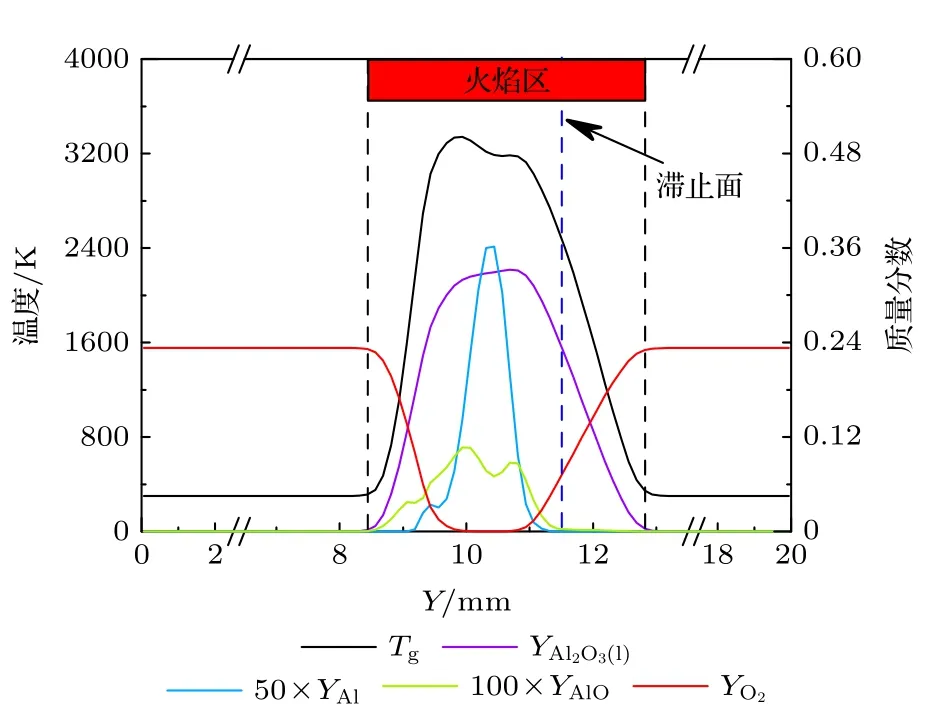
图7 铝颗粒粉尘对冲火焰轴向参数分布Fig.7.Average axial profiles across the aluminum counterflow flame.

4.3 相间传热的影响

图8 对比了不同相间换热模型对铝颗粒粉尘对冲火焰的影响,其中下标Ranz表示基于连续介质假设的Ranz-Marshall 模型,下标Kava表示考虑过度机制修正的Kavanau 模型.从图8 可以发现,不同的相间换热模型会导致完全不同的两种火焰结构.在Ranz-Marshall 模型作用下,铝颗粒粉尘对冲火焰呈现双峰结构,并且在双峰之间生成了大量的气态铝,说明铝颗粒的蒸发及之后的气相化学反应在燃烧过程中占主导地位.相反,Kavanau模型会产生一个准单峰的火焰结构,同时火焰区内气态铝的含量可以忽略,说明表面化学反应在颗粒燃烧过程中占主导地位.上述现象可从以下两个方面来解释:首先,Ranz-Marshall 模型未考虑过度机制对相间换热的影响,即高估相间传热速率,导致更快地被点燃,进而使火焰面向上游移动;其次,在Lewis 数为一的假设下,Ranz-Marshall 模型也会高估蒸发模型[(12)式]中的Sherwood 数,导致铝颗粒的蒸发速率偏大,所以对冲火焰中部产生了大量的气态铝,富余的气态铝与从氧化剂侧喷嘴注入的氧气发生气相反应,形成图中右侧的次火焰面.

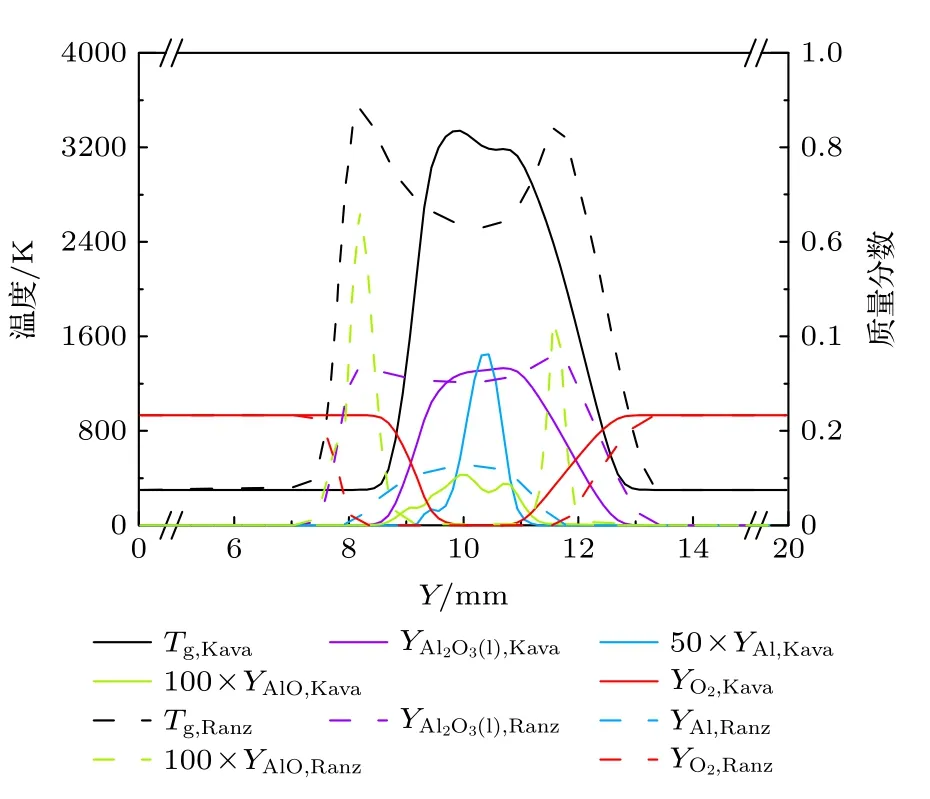
图8 不同相间传热模型对铝颗粒粉尘对冲火焰轴向参数分布的影响Fig.8.Average axial profiles across the aluminum counterflow flame using different interphase heat transfer models.

相间传热模型还会影响火焰的速度场,进而影响火焰传播速度.对于本小节的仿真工况(颗粒浓度500 g/m3,颗粒直径5.6 μm),Ranz-Marshall模型预测的火焰传播速度为49.56 cm/s,比Kavanau模型的预测值要高56%,同时也远远大于文献中的测量值(见图5).这表明传统的 Ranz-Marshall 模型高估了相间传热速率,从而导致预测的火焰传播速度偏大.

4.4 颗粒粒径的影响

颗粒粒径是影响铝颗粒燃烧的关键参数之一,因为它决定了颗粒的点火温度和燃烧时间[17].本小节研究了在铝颗粒浓度保持500 g/m3不变的情况下,颗粒粒径变化对火焰结构和火焰传播速率的影响.

图9 所示为颗粒粒径等于15 μm 的铝颗粒粉尘对冲火焰的平均气相温度(左)与AlO 分布(右)云图,其中铝颗粒的颜色分别表示其温度(左)与液态铝含量(右).与图6 相比,粉尘火焰中的颗粒变得较为稀疏,同时火焰宽度也减小.此外,如图9(右)所示,多数颗粒在被吹离计算域时仍含有大量的液态铝,说明颗粒没有完全燃烧.这是由于随着颗粒粒径的增大,比表面积减小,燃烧时间增加,导致颗粒在火焰区中的停留时间内不能完全燃烧.与较小直径的情况相比,颗粒的不完全燃烧导致滞止面附近的气体温度降低,使得液态铝的蒸发减少,从而进一步削弱了火焰中的气相化学反应.

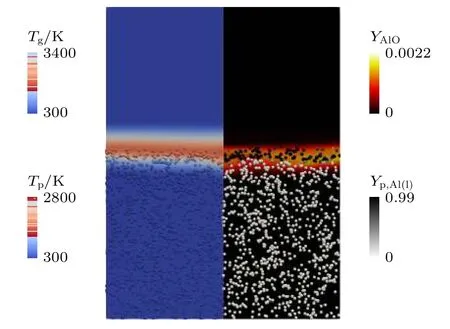
图9 对冲火焰的时均气相温度(左)和AlO 分布(右)和铝颗粒粉尘分布.颗粒浓度:500 g/m3,颗粒直径:15 μmFig.9.Time-averaged gas temperature (left) and AlO mass fraction fields (right) and instantaneous particle clouds.Dust concentration:500 g/m3,particle diameter:15 μm.

图10 所示为不同粒径的铝颗粒粉尘对冲火焰的火焰传播速度.其中Ranz表示基于连续介质假设的Ranz-Marshall 模型,Kava表示考虑过度机制修正的Kavanau 模型.从图10 可以发现,随着粒径的增加,火焰传播速度不断降低,表明整个粉尘火焰的整体反应速率降低.此外,对于颗粒直径大于10 μm 的对冲火焰,传热模型的影响可以忽略,说明此时连续介质假设是成立的.

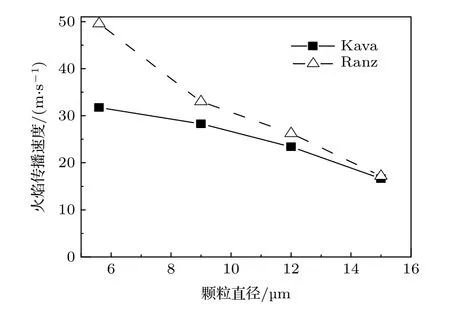
图10 铝颗粒粉尘火焰的火焰传播速度随粒径的变化Fig.10.Variations of flame speed of aluminum suspensions with particle size.

4.5 拉伸率的影响

在气相对冲火焰中,拉伸率直接决定了燃料和氧化剂的混合速率,是控制扩散火焰结构的关键参数.但是对于金属颗粒火焰,气态铝仅在颗粒熔化后通过蒸发释放,因此拉伸率对火焰结构的影响有待进一步研究.本小节在颗粒浓度保持500 g/m3不变的情况下,模拟了7 个不同入射速度的铝颗粒粉尘对冲火焰,相应的平均拉伸率为60—500 s—1.图11 所示为不同平均拉伸率下铝颗粒粉尘对冲火焰的云图.首先,随着拉伸率的增加,对冲火焰结构的高温区域不断变窄,并且火焰的反应区(AlO所在区域)由双峰变为单峰结构,从图12 中可以更直观地看出该变化.其原因主要有二:一是拉伸率较低时,颗粒在火焰区的停留时间较长,颗粒中的液态铝可以充分地蒸发并形成一个次级扩散火焰,如图11(a)所示,随着拉伸率的增加,颗粒在火焰区停留的时间减小,导致部分颗粒燃烧不完全,次级扩散火焰消失,如图11(c)及图12 所示;二是拉伸率的增大会抑制气相化学反应,降低火焰温度,从而进一步降低铝颗粒的蒸发及表面化学反应速率.可以预见的是,继续增加对冲火焰的拉伸率,铝颗粒粉尘火焰将会熄灭.

图11 不同平均拉伸率(SR)下对冲火焰的时均气相温度(左)和AlO 分布(右)和铝颗粒粉尘分布.颗粒浓度:500 g/m3,颗粒直径:5.6 μmFig.11.Time-averaged gas temperature and AlO mass fraction fields and instantaneous particle clouds of the counterflow flame under different average strain rates (SR).Dust concentration:500 g/m3,particle diameter:15 μm.

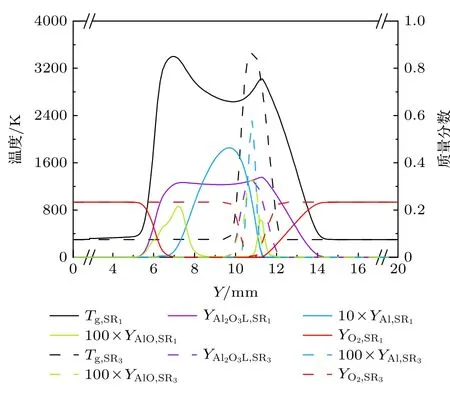
图12 不同相拉伸率对铝颗粒粉尘对冲火焰轴向参数分布的影响Fig.12.Average axial profiles across the aluminum counterflow flame with a dust concentration of 500 g/m3 under different strain rates (SR).SR1 and SR3 stand for the strain rates of 60 and 500 s-1,respectively.

图13 所示为铝颗粒粉尘火焰的火焰传播速度随拉伸率的变化规律.粉尘火焰传播速度随着拉伸率的增加而增大,呈现与气体燃料[16]和液体燃料[37]相同的变化趋势.通过简单的线性外推,可以得到未拉伸的火焰传播速度()约为29.10 cm/s,参见图13 中红色虚线.利用多项式拟合可得到一个略有差别的,但这不是本文研究的重点.需要指出的是,多数针对金属颗粒粉尘火焰的实验研究只报道了具有一定拉伸率的火焰传播速度[9,14,15],但是又缺乏对火焰拉伸率的定量描述,从图13 中可以看出,在其他条件不变的情况下,拉伸率的变化会对颗粒粉尘火焰传播速度造成一定影响,给对比分析不同文献中的粉尘火焰传播速度的数据带来一定障碍.

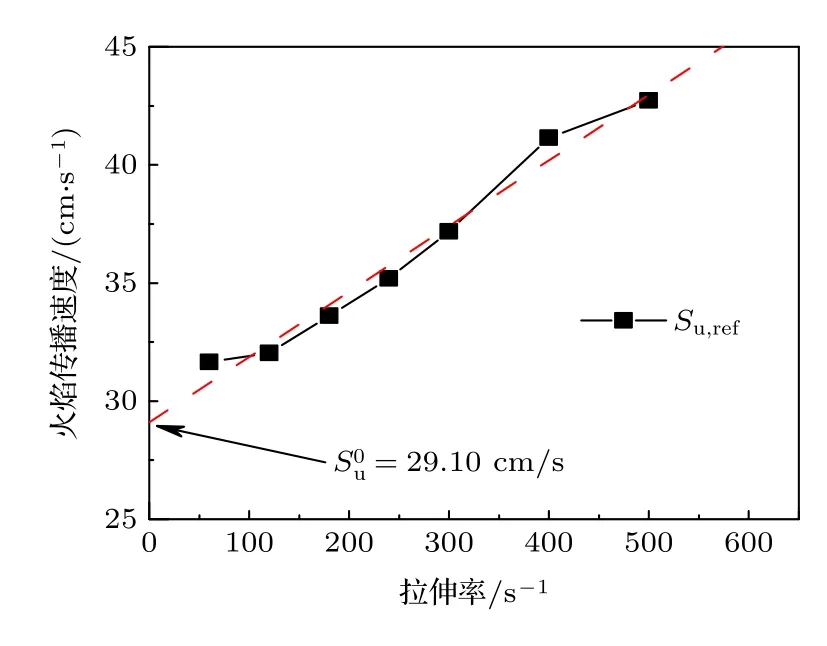
图13 铝颗粒粉尘火焰的火焰传播速度随拉伸率的变化.颗粒浓度:500 g/m3,颗粒直径:5.6 μmFig.13.Variation of flame speed of aluminum suspensions with strain rates.Dust concentration:500 g/m3,particle diameter:15 μm.

4.6 辐射的影响

图14 对比了有/无辐射传热对铝颗粒粉尘对冲火焰结构的影响,其中下标R/NR表示有/无辐射换热.从图14 可以发现,在没有辐射换热的情况下,火焰的整体温度明显升高,峰值温度增加了约680 K,说明对于铝颗粒粉尘火焰由辐射引起的热损失不可忽略.此外,由于辐射热损失引起的温度降低也会显著影响气相组分的分布,考虑辐射时,气态铝及燃烧中间产物AlO 的质量分数会显著降低,其原因将在下文进行分析.

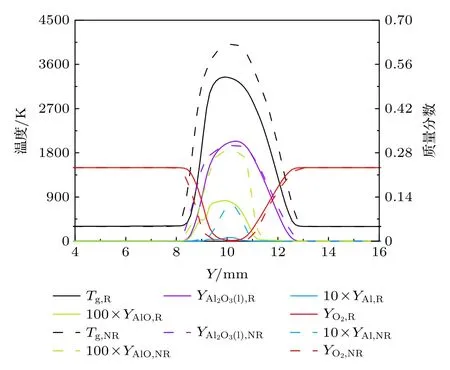
图14 辐射传热对铝颗粒粉尘对冲火焰轴向参数分布的影响.颗粒浓度:500 g/m3,颗粒直径:5.6 μmFig.14.Average axial profiles across the aluminum counterflow flame with and without radiation.Dust concentration:500 g/m3,particle diameter:5.6 μm.

图15 对比了有/无辐射传热对铝颗粒粉尘对冲火焰中离散相温度和气相温度的影响,其中下标R/NR表示有/无辐射换热.当关闭辐射时,颗粒在抵达火焰之前无法通过辐射换热被加热,因此温度保持300 K 不变,如图15 中的放大图所示.但是由于火焰整体温度升高,高温区扩大,使得颗粒在更靠近上游的位置被点燃.考虑辐射换热时,颗粒在抵达火焰区(Y=8 mm)之前温度大约上升了15 K,表明辐射换热对颗粒的加热作用比较微弱.此外,由于忽略辐射引起的热损失,火焰区内的气相温度显著升高,在相间传热作用下,离散相的温度也有一定程度增加,并更接近铝的沸点(2723 K),如图15 中绿色圆圈所示.因为在接近沸点时,气态铝的饱和蒸汽压随温度近似呈指数增加,所以虽然颗粒温度升高不明显,但会导致颗粒表面铝蒸气质量分数大幅增加.根据液滴蒸发模型(12)式及(13)式,颗粒的蒸发速率将加快并导致气相铝质量分数的增加,从而促进铝-空气的气相反应,体现在燃烧中间产物AlO 质量分数的增加,如图14 所示.

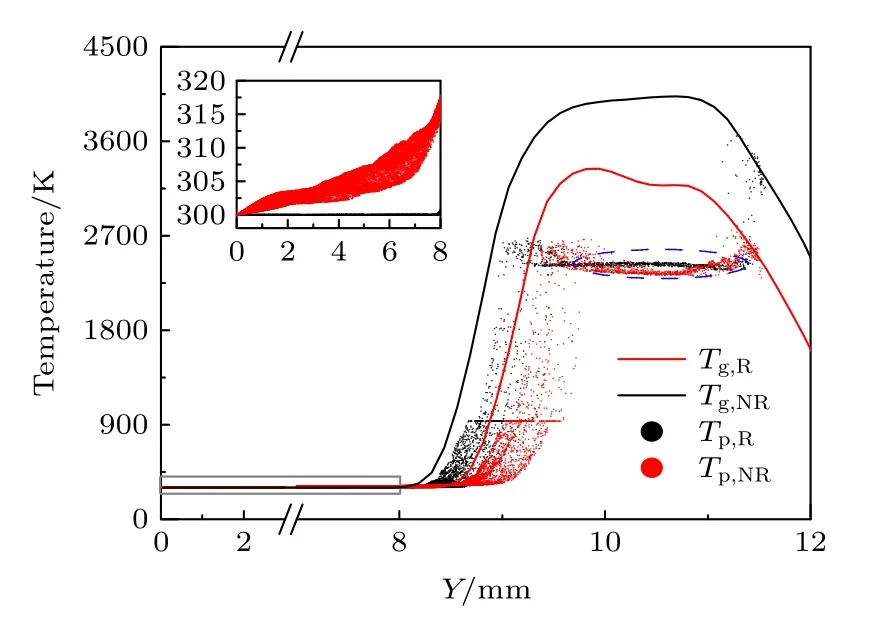
图15 有/无辐射情况下铝颗粒粉尘中的气离散相温度分布Fig.15.Scatter plot of particle temperatures with and without radiation.

5 结论

本文针对铝颗粒粉尘燃烧过程建立了考虑相间换热、相变、表面化学反应、气相反应及辐射等过程的数学模型,通过数值模拟研究了相间传热模型、颗粒粒径、拉伸率及辐射等因素对火焰结构和火焰传播速度的变化规律.首先,本文仿真了McGill 大学的铝颗粒粉尘对冲火焰,讨论了文献中利用Stokes 时间(τs)基于颗粒速度估算气相速度方法可能存在的误差,结果表明,准确的τs值是该方法的关键,而对存在一定粒径离散程度的颗粒使用单一τs值会给气相速度场的计算结果带来一定偏差,因此,本文采用直接对比离散相速度分布的方法进行模型验证,结果表明,预测的离散相速度场与实验测量值较为吻合.此外,本文预测的铝颗粒粉尘火焰的火焰传播速度与文献中的测量值也基本一致.随着颗粒粒径的增加,火焰传播速度不断降低,当颗粒粒径增大到15 μm 时,所研究工况下火焰中的铝颗粒无法完全燃烧.当颗粒粒径小于10 μm 时,连续介质假设不再成立,相间传热模型必须考虑过度区机制.火焰的拉伸率主要通过影响颗粒在火焰区停留时间而影响对冲火焰结构,随着拉伸率由60 s—1增大到500 s—1,颗粒在火焰区的停留时间减少,并出现燃烧不完全的现象,粉尘火焰由双峰变为单峰结构.火焰传播速度随着拉伸率的增加而增大,通过线性外推可得到未拉伸的火焰传播速率约为29 cm/s.辐射引起的热损失会导致气相温度大幅降低,但辐射传热对颗粒的加热作用相对较小.

本模型较为全面地反映出相间换热、表面化学反应、蒸发及热辐射对铝颗粒群燃烧的作用规律,但其中对氧化铝凝结过程的处理方法有待改进,下一步可基于凝结形核的相关理论开展铝颗粒群燃烧过程中的氧化铝凝结过程研究.