基于蒙特卡罗原理的混合颗粒三相体系声衰减计算模型研究*

2022-04-15赵宁宁肖新宇凡凤仙苏明旭

物理学报 2022年7期

赵宁宁肖新宇凡凤仙苏明旭

(上海理工大学能源与动力工程学院,上海 200093)

从单个固体和液滴颗粒的声吸收和散射特性计算入手,基于概率统计的蒙特卡罗方法(MCM),将声波以离散化的声子加以处理,通过追踪其运动历程并进行事件统计,建立一种气体介质中球形混合颗粒的声衰减预测模型.对空气中铝粉颗粒和亚微米级水滴的声衰减分别计算和验证后,将模型推广至含有混合颗粒的三相体系,对铝粉和液滴构成的单、多分散混合颗粒体系进行数值研究.结果表明:两类颗粒的声吸收特性差异明显,其散射声压均随颗粒无因次尺寸kR 的增加呈现从后向散射占主要地位逐渐过渡到前向增强的趋势.气液固混合颗粒三相体系中,颗粒类型对于声衰减影响明显、且随浓度的增加不同颗粒的衰减贡献不再遵循随混合比的线性递变关系;对于多分散体系而言,声衰减谱受平均粒径影响较大,对于粒径分布宽度参数则不敏感.模型可进一步结合数学反演形成混合颗粒体系测量的理论基础.

1 引言

气液固共存的颗粒三相体系广泛存在于石油化工、煤炭液化、生物化工、环境工程等领域,如天然气在输送过程中管道内气(天然气)液(液态水)固(水合物颗粒)[1]、电力行业脱硫塔内气(空气)液(雾)固(烟尘)[2]、化工行业气液固三相反应器内[3,4]、环境问题中气(空气)液(雾)固(霾)[5]等三相体系.气液固三相颗粒体系中颗粒粒径、相含率(各相占比)和浓度的准确监测对生产和研究均具有重要意义.图像法[3]、层析成像法[4]、光散射法[5]等测量方法已得到学者关注,而超声衰减法具备穿透性好、适应性强、非接触式测量等优点,其中三相体系的超声传播规律、声衰减预测及物理模型的建立尤为重要,需要开展专门研究.

超声在颗粒体系中传播时,会引起声学基本物理参数的变化,如声压、声速、声衰减和声阻抗等.针对两相流颗粒体系中声衰减特性的研究,Epstein 与Carhart[6]和Allegra 与Hawley[7]建立ECAH(Epstein-Carhart-Allegra-Hawley)模型,同时考虑液体介质的黏性、颗粒的弹性效应、热传导等作用,根据质量、动量和能量守恒定律,通过求解球坐标下的波动方程得到散射系数,奠定了超声波衰减理论模型的基础.之后,McClements[8-10]提出了“长波长”条件下声衰减与声速计算理论模型(McC模型),引入黏性厚度和热厚度两个参数,简化声衰减模型,研究了超声吸收衰减效应和长波长区的声衰减特性,并进行了实验验证.近年来,Parker 等[11]与Liu[12]研究了纳米颗粒悬浊液的声衰减,对颗粒体系进行测量和表征.董黎丽等[13]建立了乳浊液的声衰减反演模型,研究了多分散脂肪乳浊液的粒径分布测量问题.Wang 等[14,15]建立了耦合相修正模型,计算了空气介质中固体颗粒的声衰减.杜娜与苏明旭[16]建立了水中气泡的声散射模型,研究了有黏条件下气泡的声学特性.侯森等[17]建立了声衰减反演气泡分布模型.陈时等[18]建立了含混合气泡液体中的声传播模型.郭盼盼等[19]、李运思等[20]和Huang 等[21]建立了蒙特卡罗原理的声衰减计算模型,应用于液固两相、液液两相单分散和多分散体系的声衰减谱预测.

对两相体系中颗粒的声衰减特性研究已经趋于成熟,但是对于气体介质中液、固混合颗粒构成的三相体系,其声传播规律和声衰减计算仍属难题.此外,实际的混合颗粒系粒径分布并非均一,而是呈现多分散分布,ECAH 模型等均不能直接应用.因此,作者通过引入蒙特卡罗方法,利用其数理统计的特点,研究一种适用于三相、混合多分散颗粒体系的超声波衰减模型.

2 模型

蒙特卡罗方法是一种以概率统计理论为基础的数值方法,可将其引入到颗粒两相及多相流的模拟计算[19-23].类比于光散射计算中的“光子”概念,其核心思想是将入射声波按照“声子”概念抽象并离散化处理,即将换能器发出的连续超声波离散成大量时序上相互独立的声子.

如图1 所示,气液固三相体系中混合了两类球形颗粒,蓝色为液滴颗粒,红色为铝粉颗粒,介质为空气.结构参数L为发射器(T)和接收器(R)之间距离,d为接收器的直径,H为上下边界距离,ln为第n次(n=1,2,3···)随机散射后声子运动自由程.发射器发射声波能量表示成大量非连续的声子并对其进行追踪.声子行为包括透射、吸收、越界或者复散射后被接收器接收.通过统计接收器获取声子数,即可模拟在一定的颗粒粒径、体积浓度和超声频率条件混合颗粒系中声波行为并计算声衰减系数.

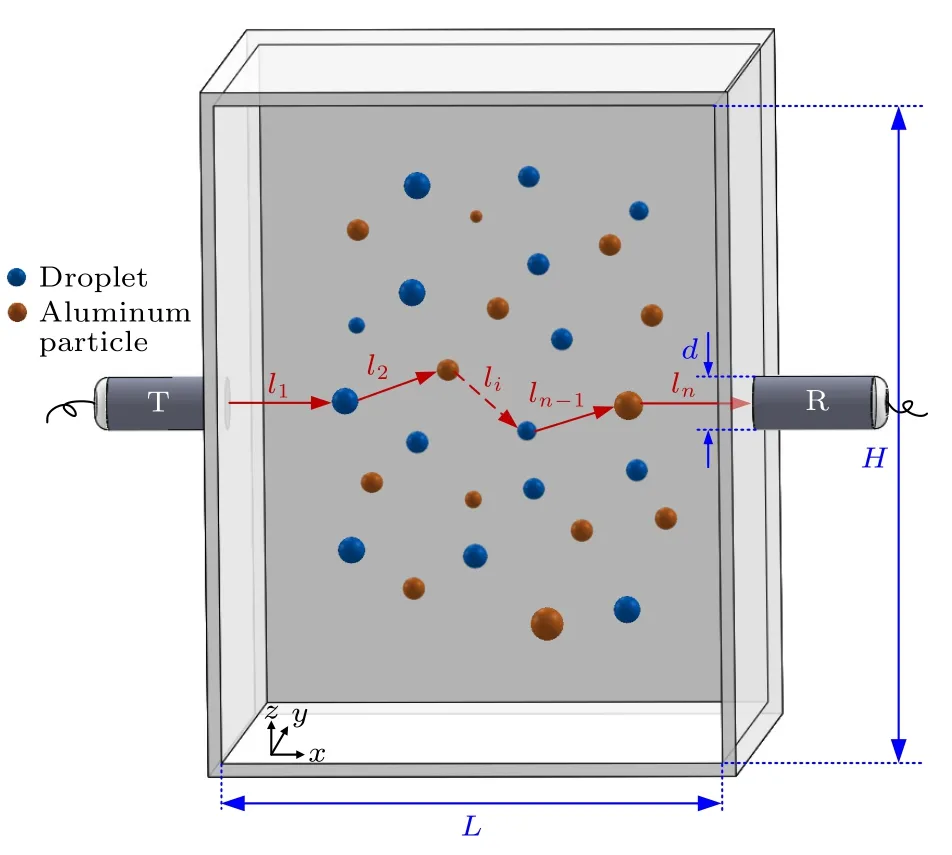
图1 声子在混合颗粒体系中传播过程Fig.1.Schematic of a phonon propagation through a mixed particle system.

鉴于本文涉及混合颗粒的气液固三相体系,当声子和颗粒发生碰撞时,须判断颗粒类型,即铝粉或液滴:

式中,ε1是在[0,1]区间内服从均匀分布的随机数;混合比φ为液滴在整个混合颗粒体系中所占的数目比,例如φ取0 时颗粒全为铝粉,1 时则全为液滴.

下一步,判断声子碰撞颗粒后可能发生事件,定义声散射系数和消声系数比值P:

其中消声系数QTQa+Qs.Qa和Qs分别为声吸收系数和声散射系数,由Hay和Mercer[24]方法算得.接下来,根据设定条件判断声子的下一事件:

式中,ε2是[0,1]区间服从均匀分布的随机数;n为散射次数;x为声子沿着x方向运动的路程;z为声子沿着z方向运动的路程.通常进入气液固三相体系声子可能被颗粒吸收、被接收器直接接收(透射)、越界逃逸或复散射.前三种情况下,声子历程终止,而对于复散射,则需进一步追踪声子.

在空气中传播的声子遇到颗粒发生声散射,需确定声子散射方向及声子两次散射之间的自由程.采用(4)式计算归一化散射声压f(θ):

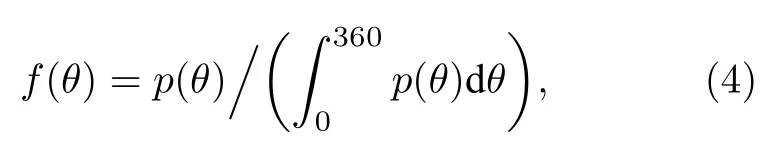
式中,θ为散射角,取值范围为0到360°.p(θ)是颗粒表面散射声压分布函数(颗粒为球形时与方位角无关),对于弹性固体颗粒,可由Faran 理论计算[25],对于液滴颗粒,采用液体球的散射声压计算方法[26].(5)式和(6)式分别给出其核心计算式:

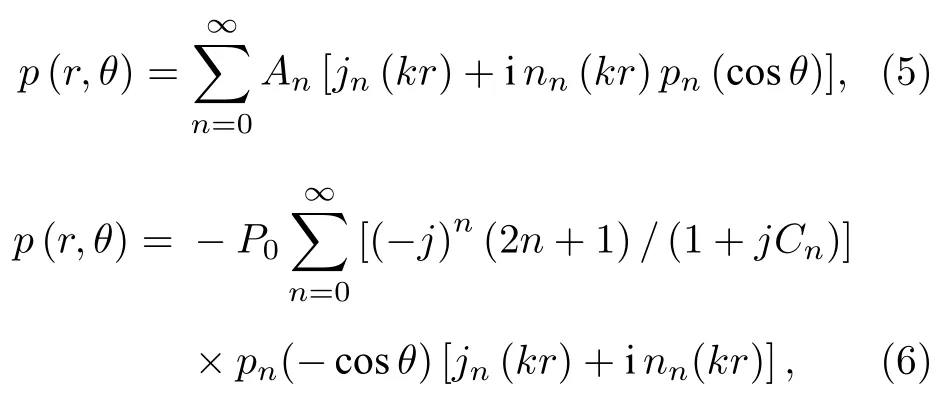
式中,jn和nn分别是第一类球Bessel 函数和第二类球Bessel 函数,k为入射声波波数;r为接收点距离,取颗粒半径的100 倍;Pn(cosθ)是勒让德多项式,散射系数An由Faran理论算出.

为确定声子出射方向,将散射角θ从0到360°划分为360 份,引入另一随机数ε3与归一化散射声压分布f(θ)比较,如果:

则声子散射后的出射角就为θM,M取值范围为1—360.之后确定随机散射声子的自由程l:

ε4是在[0,1]区间服从均匀分布的另一随机数.

重复(2)式—(8)式的声子运动过程,在确定经过n+1次散射后声子仍在颗粒体系中后,可得其散射坐标:

式中,xn和zn是声子第n次散射后的位置.至此,所有声子都要经历上述过程,根据(3)式条件判断并统计其最终去向,模型中声子运动全过程可由如下流程图所示,可得声衰减系数计算公式为

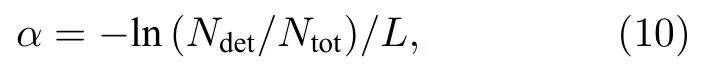
式中,Ndet是探测接收器接收声子数目;Ntot是声子样本容量.蒙特卡罗模型的算法流程图如图2 所示.

图2 蒙特卡罗模型的算法流程图Fig.2.Flow chart of Monte Carlo model.

3 计算过程和结果验证

3.1 单颗粒声散射

计算对象铝粉和液(水)滴颗粒的物性参数见表1,为比较不同类型颗粒的声散射和声吸收特性,定义系数Ps为液滴与铝粉颗粒声散射系数Qs之比,Pa为液滴与铝粉颗粒声吸收系数Qa之比.在超声频率为20 kHz、体积浓度为0.01%、颗粒半径为0.1—1 μm 时,计算其随颗粒半径变化情况.由图3可知,两类颗粒的声散射特性较接近,而吸收特性差异明显并随颗粒半径变化,同粒径下,铝粉颗粒声吸收更强,对应声衰减也会更大.

图3 液滴和铝粉的声散射及吸收系数比Fig.3.Ratio of scattering and absorption coefficients of droplet and aluminum particle.

表1 数值计算中介质和颗粒物性参数(25 ℃)Table 1.Parameters in the numerical simulation (25 ℃).

由于低频条件下空气中固体和液滴颗粒散射特性差异不大,图4 仅给出液滴的归一化散射声压((6)式计算).定义平面声波传播方向即图中0°—90°和270°—360°为前向,反之即为后向.当无因次参量kR=0.5和kR=1 时,颗粒后向散射比较均匀且占主要地位;此后随着无因次参量的增大,散射旁瓣增多,前向散射效应逐渐增强、向前集中,且前向主瓣散射角变小.如前所述,单颗粒的吸收和散射结果将直接耦合到模型中用于确定声子的吸收概率和出射方向.

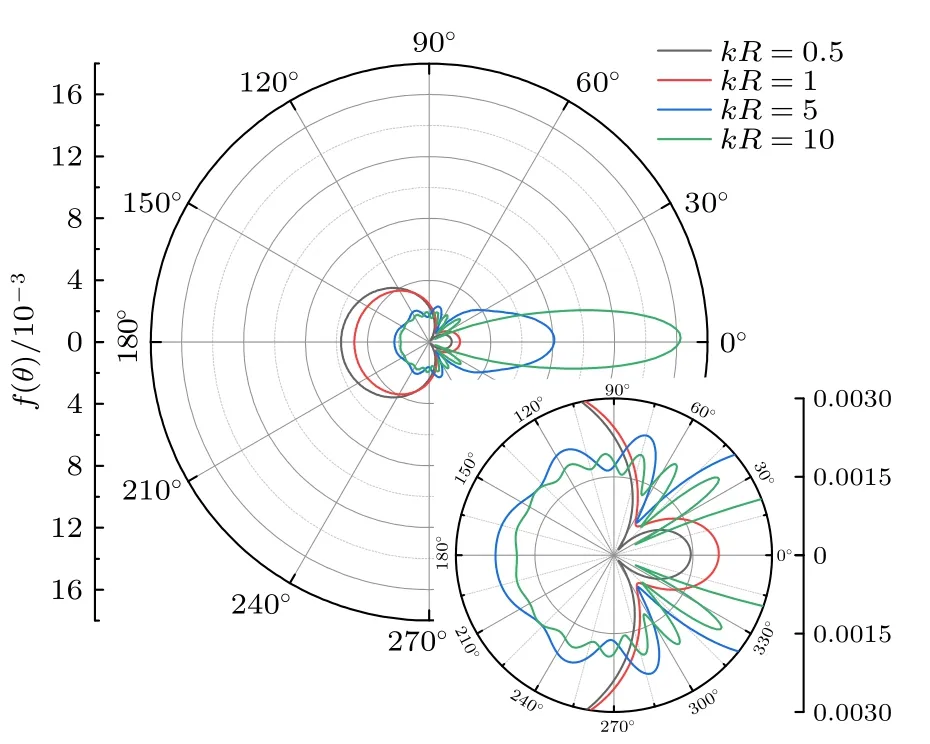
图4 液滴颗粒散射声压Fig.4.Scattering pressure of droplet.

3.2 声子统计

采用蒙特卡罗方法计算声衰减系数时,其计算精度受限于声子的样本容量,样本容量越高,精度越高,图5(a)展示了液滴颗粒体系在声波频率为50 kHz,颗粒半径为0.1 μm,体积浓度为0.01%时,分别采用1×104,1×105和1×106样本容量,计算100次统计衰减系数平均值和相对偏差.可知采用声子1×106样本容量,数据相对偏差在—0.59%至0.57%,此时样本容量足够大,模拟结果受随机因素影响的波动较小.

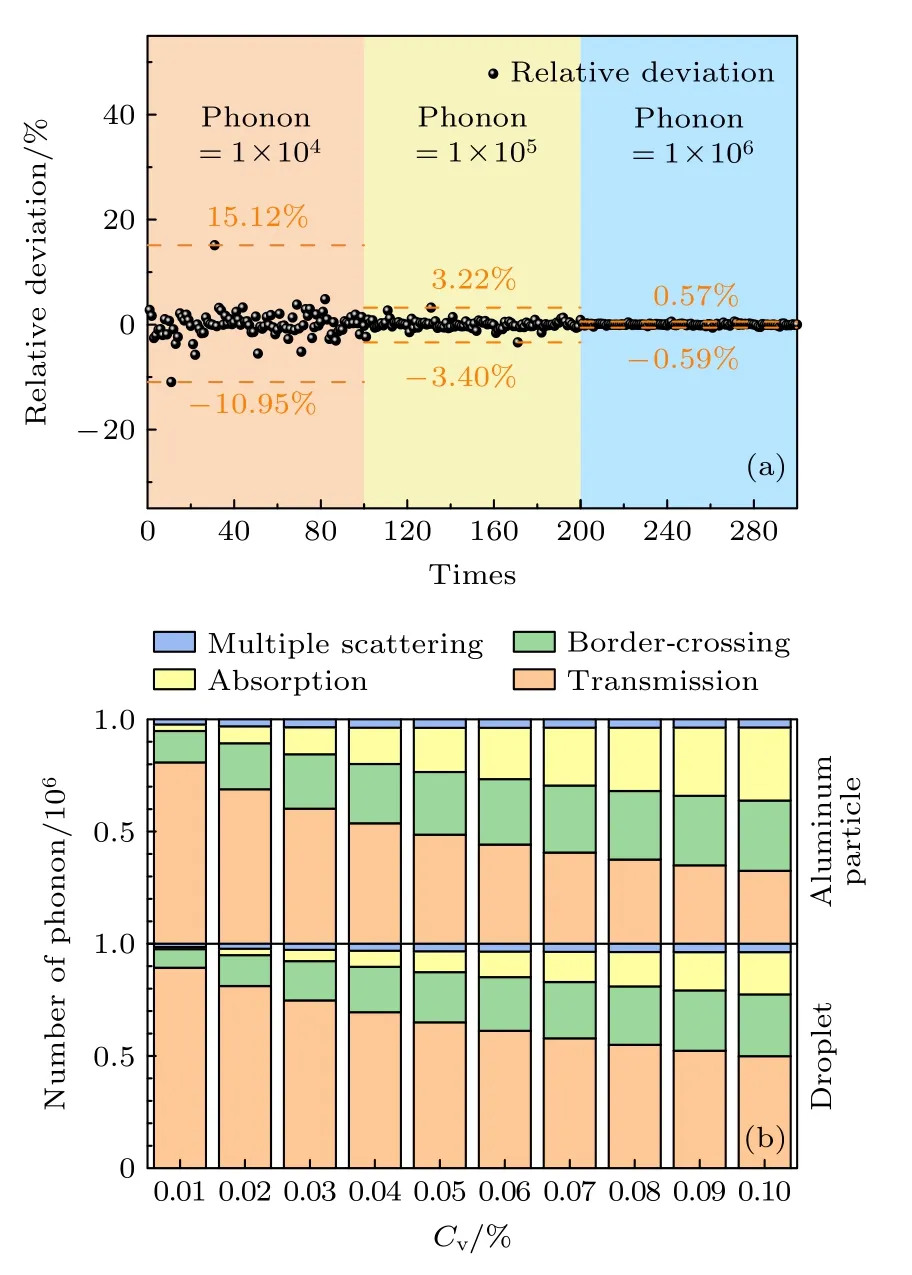
图5 不同条件声子统计结果 (a) 不同声子数目时相对偏差;(b) 不同体积浓度时声子去向Fig.5.Statistic of phonons under different conditions:(a)Relative deviations at different number of phonons;(b)phonon events at different particle volume concentrations.

为研究气体介质中声波传播物理过程和声子最终去向,对于铝粉、液滴颗粒体系,设定声波频率为20 kHz,颗粒半径为0.1 μm,体积浓度为0.01%—0.1%,声子样本容量为1×106.分别统计了声子发生复散射、吸收、越界以及透射去向的数量.

统计结果如图5(b)所示,声子主要历经吸收和直接透射过程.随体积浓度增加,声子在运动过程中与颗粒碰撞概率加大,碰撞后的散射声子易偏离接收范围,表现为透射声子数减少,而越界的声子数递增.同时,经历复散射过程的声子数逐渐增加,但其数目总量不大(小于 4×104),小于越界逃逸和被吸收声子数,因此并不占主导地位.对于两种类型颗粒,被吸收声子数差异明显,这由不同类型颗粒自身吸收差异决定(如3.1 节),从而对声衰减影响亦不同.

3.3 模型验证

为验证本文发展蒙特卡罗模型和声衰减计算程序准确性,首先对单一类型颗粒两相体系,计算了不同粒径下声衰减系数数值,将结果和经典ECAH模型以及McC 模型预测结果进行对比(对比模型结果均通过文献公式编程运算而得).图6(a)给出液滴、铝粉颗粒在体积浓度Cv=0.01%,超声频率f=50 kHz 时采用蒙特卡罗方法、ECAH 模型、McC 模型三种结果对比.由图6(a)可知,三种模型的计算结果较为吻合.在体积浓度和频率一定条件下,受颗粒的黏性耗散和热耗散影响,声衰减系数随着颗粒半径增大呈现先增后减变化趋势,该声衰减极大值位于0.2—0.4 μm 之间.计算条件为颗粒半径0.1 μm、体积浓度0.01%、频率50 kHz 时,各物性参数分别单独增加10%条件下,声衰减系数对颗粒物性参数的敏感性如下图6(b).由于颗粒相和连续相之间的高密度差,颗粒的黏性耗散和热耗散效应对声衰减结果的影响最大,其相关物性参数主要为颗粒密度(铝粉19.12%、液滴19.54%)、比热容(铝粉4.35%、液滴17.30%)、导热系数(铝粉1.39%)、声吸收系数(液滴0.42%).

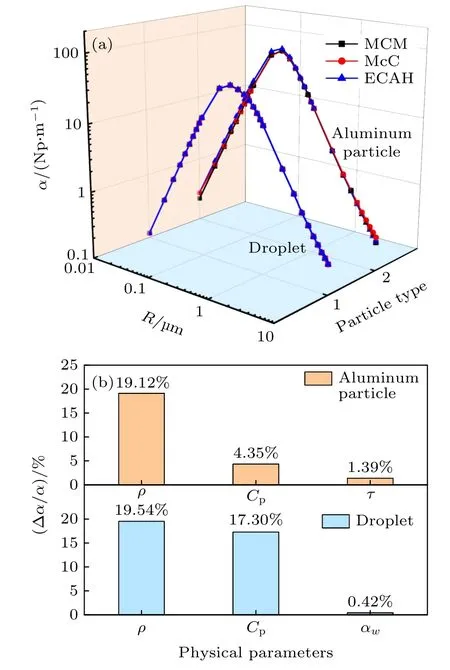
图6 模型验证及物性敏感性 (a) 声衰减系数随颗粒半径变化;(b) 声衰减系数随颗粒物性参数变化Fig.6.Model validation and the sensitivity of physical parameters:(a) Ultrasonic attenuation coefficient varies with the particle radius;(b) ultrasonic attenuation coefficient varies with the particle parameters.

将蒙特卡罗方法计算结果分别与铝粉颗粒和液滴颗粒的实验结果对比.可以看出,无论图7(a)所示铝粉颗粒在半径R=2.8 μm,质量浓度Cm=0.032 kg/kg 条件下声衰减系数[14],还是图7(b)所示液滴颗粒在超声频率f=40,200 kHz,体积浓度Cv=0.0043%,0.0114%条件下声衰减系数[27],同等条件下作者采用蒙特卡罗方法的数值计算结果与实验数据整体吻合.

图7 实验结果对比 (a) 铝粉颗粒;(b) 液滴颗粒 (R1和R2 分别为文献中超声和图像法测得液滴半径)Fig.7.Comparison with experimental results:(a) Aluminum particle;(b) droplet (R1 and R2 are droplet radius measured by ultrasonic and image method in the reference respectively).

4 混合颗粒系结果

4.1 单分散系

对单一类型固体颗粒、液滴颗粒的计算和验证表明蒙特卡罗模型从建模思路到编程可靠,但在实际测量对象中,常包含多种类型颗粒,因此进一步将其拓展至铝粉-液滴混合颗粒三相体系.

对于单分散混合颗粒三相体系,图8 所示为频率f=40 kHz,颗粒半径R=0.1 μm,不同体积浓度条件下声衰减系数随颗粒数目混合比的变化曲线.由图8 可知,随着混合比φ增大即液滴所占比例增大(φ为1 时全为液滴),混合颗粒体系的声衰减系数逐渐减小,说明液滴颗粒对声衰减的贡献较铝粉颗粒小.在体积浓度较低时(如Cv=0.01%),声衰减系数随混合比近似呈现线性变化,而随着体积浓度的进一步增加,尤其到0.05%,出现非线性变化趋势,由于体积浓度增加,声子碰撞概率增加,铝粉颗粒的声吸收作用进一步强化.值得注意的是,根据图示声衰减谱,在已知体积浓度和颗粒粒度前提下,可利用反演问题求解颗粒体系的混合颗粒数目比,从而获知不同类型颗粒混合时的占比信息.

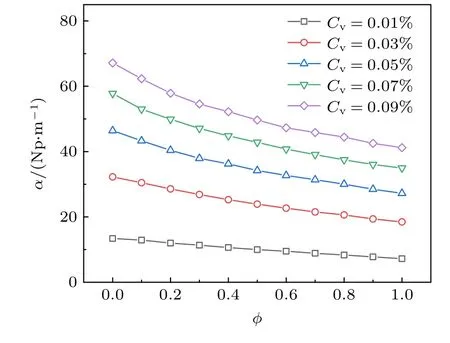
图8 单分散三相混合体系声衰减Fig.8.Ultrasonic attenuation coefficient in monodisperse mixed system.

4.2 多分散系

实际的颗粒系中粒径往往并非均一(即非理想的单分散系),对于呈多分散分布混合颗粒三相体系,假设颗粒粒径分布服从正态分布函数,即:

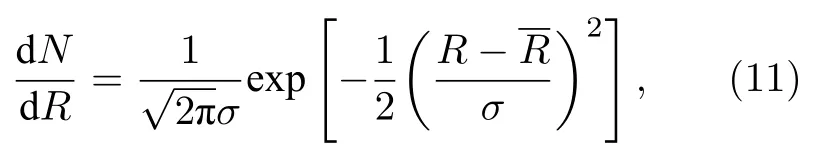
其中N为颗粒数目;R为特征尺寸参数(函数期望值);σ为分布宽度参数(函数标准差).

设定混合颗粒系的粒径分布为双峰模态,两类颗粒占比均为0.5,铝粉颗粒特征尺寸参数R1为0.10 μm,分布宽度参数σ1为0.015 μm;液滴颗粒特征尺寸参数R2为0.15 μm,分布宽度参数σ2分别为0.010,0.015和0.020 μm,另外设定一组R1为0.10 μm,R2为0.15 μm,σ1=σ2=0 的无分布宽度混合颗粒组对比,颗粒混合后的粒径分布如图9 所示.

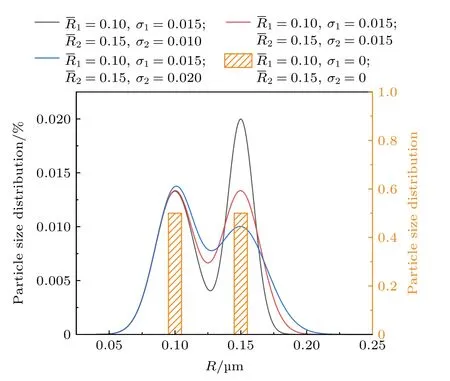
图9 混合颗粒体系粒径分布Fig.9.Particle size distribution of mixed particle system.

图10(a)为体积浓度Cv=0.02%,四种不同粒径分布组合下声衰减谱曲线,可知在频率低于40 kHz 时,液滴粒径分布参数的变化对声衰减谱影响较小,只有在足够频率带宽(如至100 kHz)的谱,能较好地同步分析平均粒径和分布信息.图10(b)为频率f=40 kHz,声衰减系数随体积浓度增加曲线呈现非线性变化趋势,结合图5(b)中复散射声子讨论,说明颗粒体系中发生复散射的概率增大,进而引起衰减系数的增长趋势变化.此外,与分布宽度为零的单分散混合颗粒的结果对比,正态分布的多分散体系由于颗粒尺寸落在衰减峰值区外,导致分布宽度参数越大,声衰减数值越小.同样,当两种颗粒分布有重叠或不同比例时,超声衰减谱同样具备差异性,可以有效区分不同混合比时的声衰减结果.

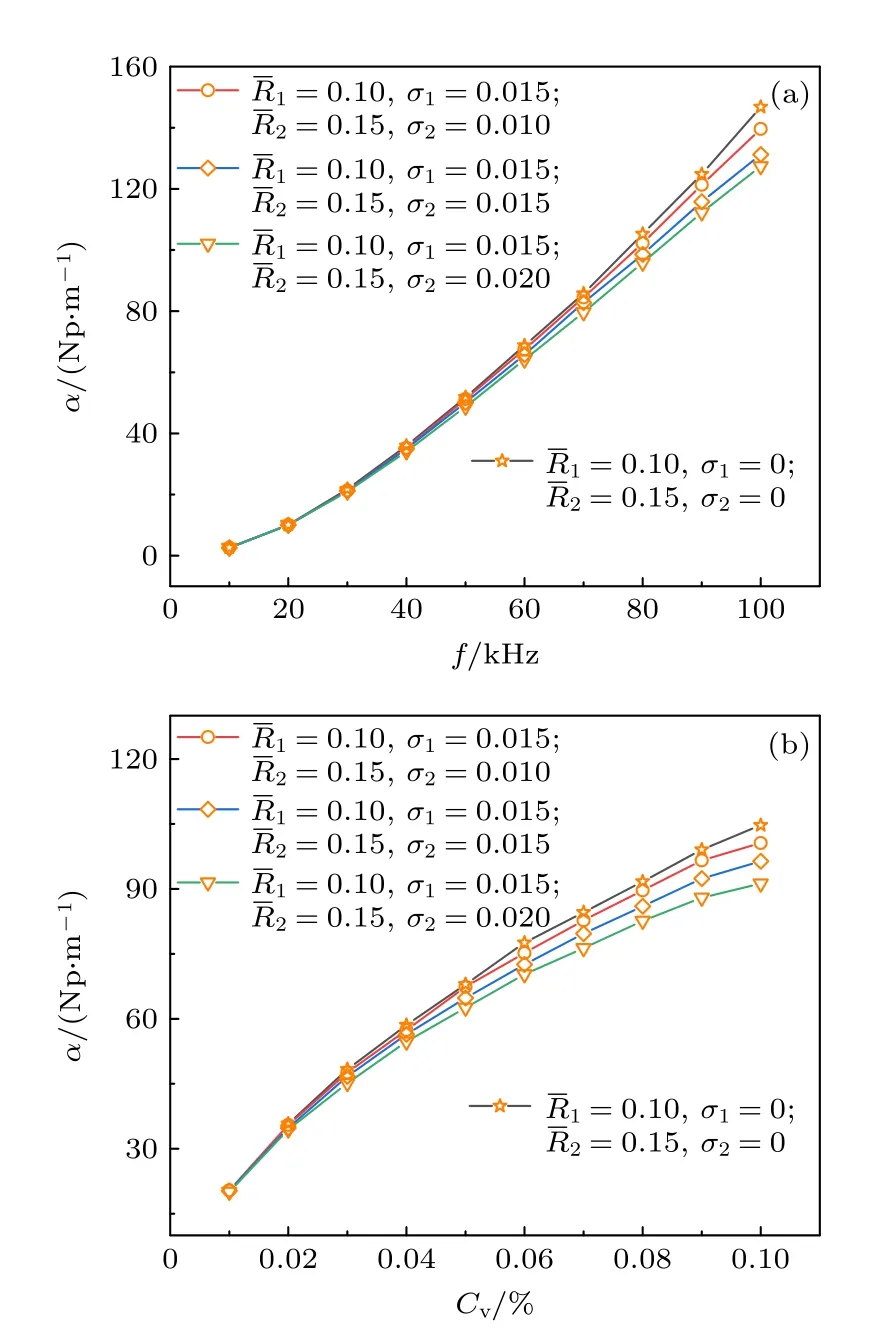
图10 多分散三相混合体系声衰减 (a) 随频率变化;(b) 随浓度变化Fig.10.Ultrasonic attenuation coefficient in polydisperse mixed system:(a) Curves with frequency;(b) curves with volume concentration.