平动小目标光子探测回波特性及测距误差研究*

侯阿慧 胡以华† 方佳节 赵楠翔‡ 徐世龙

1) (国防科技大学,脉冲功率激光技术国家重点实验室,合肥 230037)

2) (国防科技大学,安徽省电子制约技术重点实验室,合肥 230037)

针对远距离运动目标的光子测距问题,建立了运动目标的光子探测回波概率分布模型,给出了适用于任意目标的光子探测蒙特卡洛模型.通过实验对比,验证了蒙特卡洛仿真模型的正确性.进一步分析了一个探测周期内的平动小矩形目标激光回波和光子回波概率分布变化规律,讨论了光子测距误差与目标平动速度间的关系.结果表明:光斑直径为 2.5 m、目标尺度为 1m时,距离漂移在速度为 25 m/s取到极大值 6.72 cm,是扩展目标距离漂移的 1/2 倍;随着平动速度的增加,以出光斑为界,距离漂移先增大后保持稳定不变.本文提出的方法可进一步扩展到其他形状、材质、姿态、运动目标的光子探测,研究结果为运动目标的光子测距的校正和性能的提升提供了理论依据.

1 引言

激光雷达能精准探测目标的距离、形状和运动轨迹[1,2].当前大多数激光测距雷达工作在传统线性模式,为保证足够的信噪比,接收的回波光子数至少需要几百个[3,4].光子计数激光雷达采用单光子探测器,具有灵敏度高、时间分辨率高、时间抖动小和测距精度高的特点,被广泛应用在激光测距[5,6]和目标探测[7]领域.光子测距通过利用单光子探测器和时间相关光子计数器,测量每个光子事件的飞行时间以实现测距的目的[8,9].由于单光子探测器时间的存在,光子探测出现首光子偏置效应[10],使得光子回波概率分布产生较大畸变,导致光子测距出现了距离漂移.Oh 等[9]对光子测距误差进行了理论和实验对比,首次提出了光子测距距离漂移,并给出了校正方法;黄科等[11]和Chen 等[12]深入分析了回波光子数和发射激光脉宽与光子测距误差的关系,分别提出了基于理论公式的校正补偿方法和采用多探测器进行校正补偿的方法.上述研究侧重于分析光子探测系统参数对光子测距误差影响,未考虑光子测距误差与目标特征间的关系.

寇添等[13,14]分析了简单空中目标态势对激光回波脉冲的影响,提出了一种新的测距精度的描述方式;徐孝彬等[15]推导了平面目标的激光回波解析表达式,分析了目标参数对激光测距误差的影响;谢庚承等[16]简化了飞行目标模型,研究了静止飞行目标姿态的变化与脉冲激光测距回波特性和测距误差的关系;Xu 等[17]对简单三维目标的脉冲激光回波分布进行了数值仿真和实验验证.上述研究偏向于激光雷达传统探测模式下的静止目标特性与测距误差的关系研究.侯阿慧等[18]建立了扩展目标的光子探测回波概率模型,讨论了不同扩展目标不同倾角的光子测距误差.然而,目前的文献缺乏对运动目标的光子测距相关研究.刘芳华等[19]设计了一种适用于运动小目标高速测距的光子计数激光雷达,可获得径向运动目标的距离和速度,但其测距误差在 0.11 m 左右,光子测距误差较大.由文献[20]可知,光子测距的过程是:通过累计探测得到目标回波光子事件到达时间的统计直方图,计算求得目标的光子回波概率分布,结合质心算法,最终获得目标的距离.当目标静止时,探测过程中的激光回波波形基本相同,光子事件服从的概率分布相同,累计得到直方图分布仅受限于探测次数;目标运动时,探测过程中,目标回波波形具有较大差异,不同时刻的光子事件服从的概率分布都在发生变化.因此,研究运动目标的光子测距误差具有重要意义.

本文建立了运动目标的光子探测回波概率分布模型,实现了光子探测回波概率分布的蒙特卡洛仿真,通过实验对比验证了蒙特卡洛仿真的正确性;针对平动小目标,仿真对比了一个探测周期内的激光回波和光子回波概率分布的变化特征,讨论了光子测距误差与平动速度的变化规律.

2 运动目标光子探测回波概率分布模型

2.1 运动目标光子回波概率分布理论模型

运动目标光子探测的坐标示意图如图1 所示.激光的光斑在xoy平面,激光在z轴的负半轴,与坐标原点的距离为r0,发射激光具有周期性,可直接讨论单个脉冲.

图1 运动目标光子测距坐标系示意图 (a) xyz 坐标系;(b) xoy 面Fig.1.Coordinate system of photon ranging for moving targets:(a) xyz coordinate system;(b) xoy plane.

发射激光服从三维高斯分布,沿着z轴传输,可表示为

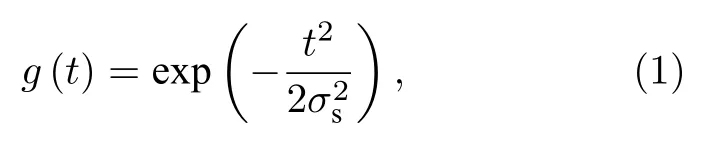
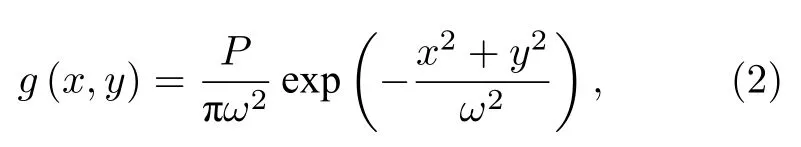
式中,σsFWHM/,FWHM 为发射激光的半高全宽;P为发射激光峰值功率;ω为面元处激光光斑半径,ω=(z+r0)φ0,φ0为发射激光半发散角.

目标始终处于运动状态,其位置坐标始终在变化.一般情况下,光子计数激光雷达的发射激光脉宽至多为 ns 级别.因此,在单个脉冲内目标可认为是静止状态.运动目标的坐标表示为

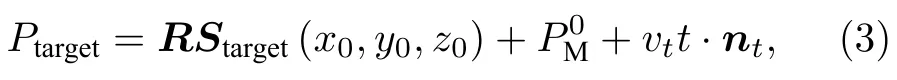
式中,Ptarget为运动中的目标位置,Ptarget(x,y,z) ;为目标中心初始位置;Starget为目标各点相对目标中心位置的点集合,不同点集合表征不同目标形状;R为姿态变换矩阵[18],可利用姿态变换矩阵获得目标姿态变换后的点集合;vt为目标的运动速度;nt为目标运动的单位方向向量;t为时间.

分别计算每个脉冲的激光回波,第k个脉冲的激光回波计算[17]:

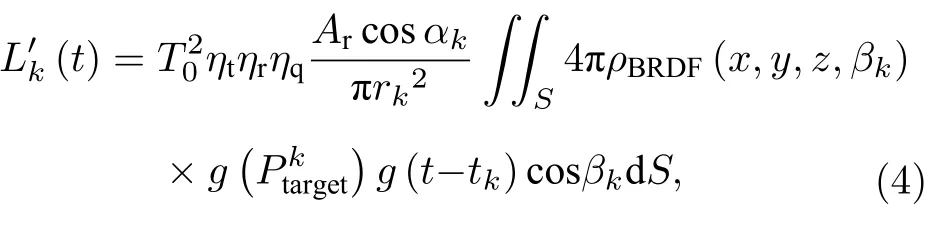
式中,T0为大气单程通过率;ηt和ηr分别为发射和接收系统的系统效率;ηq为单光子探测器的探测效率;Ar为探测系统的接收面积;ρBRDF(x,y,z,βk) 为目标的双向反射率分布(bidirectional reflectance distribution function,BRDF),反映目标的材质信息;tk为面元的时间延迟,,c为光速;βk为面元法线与激光传输方向的夹角.

第i时间间隔内的平均信号回波光子数Nk(i)为单光子能量;基于泊松响应分布模型[21],第k个激光脉冲在第i时间间隔的探测概率为

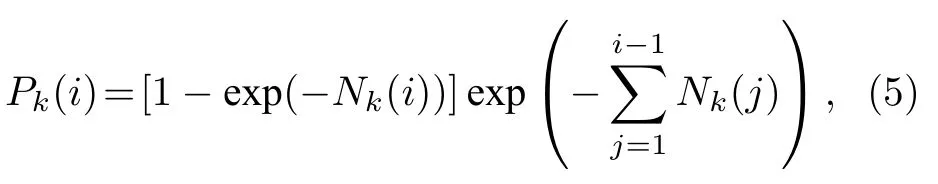
式中,Nk(i)为第i时间间隔内的平均回波光子数,Nk(i)Nks(i)+Nn,Nn为单个时间间隔的平均噪声光子数.

光子探测常采用累计探测的方式.即在探测时间段内进行累计探测,通过时间相关光子技术(timecorrelated single-photon counting,TCSPC)的处理,得到光子事件到达时间的统计分布:

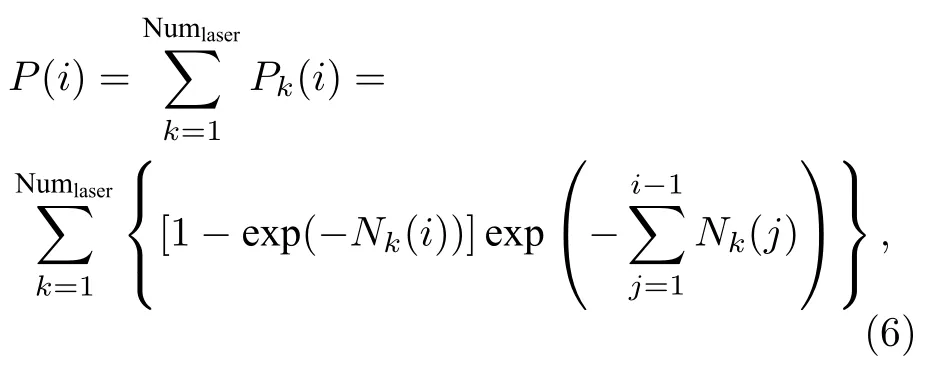
式中,Numlaser为激光发射次数,NumlaserLRF·Δt;LRF(laser repetition frequency)为发射激光重复频率.

至此,获得了运动目标的光子测距的光子波形,与发射激光重复频率、目标运动速度密切相关.

本文将P(i)表示为P(i|LRF,vt) .

2.2 光子探测蒙特卡洛模型

光子探测蒙特卡洛模型,基于发射激光与目标特征的作用,考虑发射激光重复频率、单光子探测器的死时间和系统单次探测时间周期等时间因素,模拟光子随机到达探测器被系统探测的整个物理过程,最终获得光子回波概率分布.流程图如图2所示.其中,目标调制表现为任一时刻目标形状、材质、姿态、运动等导致目标点集合和BRDF 参数的变化,进而改变回波光子时空分布的过程.

为验证光子探测蒙特卡洛模型的正确性,对目标为静止的扩展平面目标进行光子回波分布仿真.发射激光重复频率为 5kHz,死时间为 1μs,单次探测周期为 1 s,蒙特卡洛仿真结果和与文献[18]中图2 的结果对比如图3 所示.

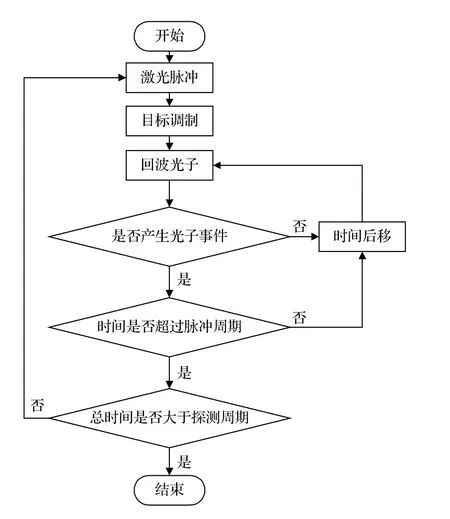
图2 光子探测蒙特卡洛模型流程图Fig.2.Flow diagram of photon detection Monte Carlo model.

如图3 所示,蒙特卡洛仿真结果与理论计算和实验结果基本吻合,表明了光子探测回波概率分布蒙特卡洛模型的正确性,为接下来的平动目标的光子测距误差分析奠定基础.

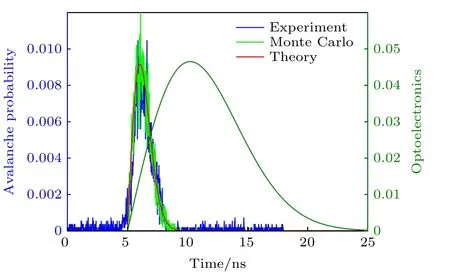
图3 蒙特卡洛模型仿真结果对比Fig.3.Comparison of Monte Carlo model simulation results.

3 平动小目标的光子测距误差分析

设置目标为矩形平板,尺寸为 1m×0.5 m ;发射激光半高全宽为 1ns,单脉冲能量为 1μJ,全发散角为 0.25 mrad,激光重复频率为 5kHz,探测距离为 10 km,扩展目标为朗伯体,反射率为 0.9 .光子探测的单次累计探测时间为 0.1 s,时间栅格宽度为 128 ps .为便于描述,将光子回波概率分布简称为光子波形.

3.1 平动小目标的回波特性分析

光子测距中,目标的平动会带来激光回波强度的变化.在探测过程中,激光回波常常通过多脉冲平均获得;光子波形则为光子事件到达时间的统计直方图.

目标处激光光斑直径为 2.5 m,目标的长度为1 m,当目标的平动速度为 35 m/s 时,单个探测累积时间内目标恰好穿过光斑,不同时刻的被照射目标面积Atarget和激光回波单脉冲光子数Nlaser的分布如图4 所示,横坐标Dm为探测距离内目标平动的距离.

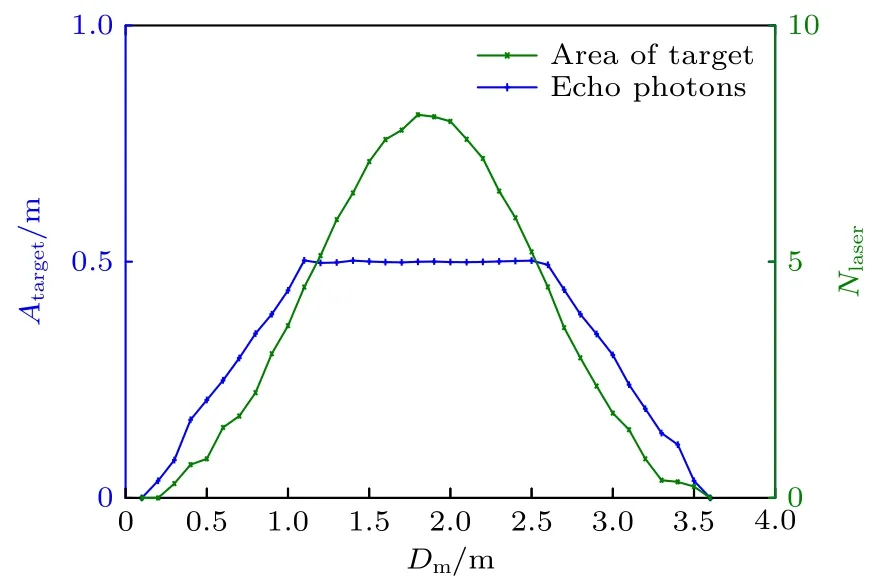
图4 目标面积和回波光子数与目标平动距离的关系Fig.4.The relationship between the area of target,the number of echo photons and the target translation distance.

由图4 可知,随着运动时间变化,被照射目标面积先增大后减小,在整个目标面积最大值保持一段时间稳定;发射激光与目标作用后,回波单脉冲光子数的变化呈高斯型,最高处可达9 个光子.由文献[11]可知,回波强度不同,光子波形具有较大差异,距离漂移随之变化,又由于光子事件的随机性,探测时间内形成的光子波形具有较大不确定性.为直观理解,利用光子探测蒙特卡洛模型,仿真得到一个随机的光子波形,如图5 所示.

如图5 所示,绿色虚线为探测时间内的平均激光脉冲回波,脉冲光子数为 3.811,蓝色虚线是基于平均激光脉冲回波计算得到的光子回波概率分布,简称为平均光子波形;红色实线为平动目标的理论光子波形,黑色实线为蒙特卡洛仿真的随机光子波形,其中总发射激光脉冲数500,探测得到的总光子事件数为 407 .不难发现,探测到的光子事件数仅占总发射激光脉冲数的81.4%,这是由于探测周期的部分时间内,目标不在激光光斑内或回波光子强度极少,没有触发单光子探测器,进而没有产生光子事件.由图5 可得,相较于平均光子波形,平动目标的光子波形具有更大的距离前移,会使得光子测距产生更大的距离漂移.分析原因,距离漂移随回波光子数的变化为凸函数,距离漂移的累计值要大于平均回波光子对应的距离漂移.

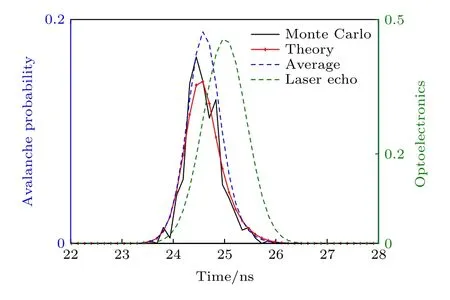
图5 v=35 m/s 时目标的光子探测概率分布结果Fig.5.Results of the photon detection probability distribution of the target at v=35 m/s.

3.2 平动小目标的测距误差分析

为定量描述平动目标运动速度与光子测距误差的关系,结合质心算法[11,12],可得光子探测的时间均值和发射激光的时间均值:

式中,Tp为探测距离门的时间宽度.

光子探测的光子回波概率分布相较于激光脉冲回波质心前移对应的距离定义为光子测距的距离漂移Rwe:

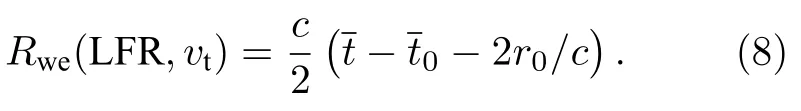
本文仅讨论了距离漂移与目标平动速度间的关系.

首先对不同目标平动速度的光子波形进行了理论数值计算和蒙特卡洛仿真,结果如图6 所示.进一步比较分析,对扩展目标的光子波形也进行了计算,见图6 中的蓝色虚线.在本节讨论中,扩展目标特指在运动过程中被照射部分始终等于激光光斑的平面目标,该平面与激光传输方向垂直.

如图6 所示,目标平动速度小于 25 m/s 时,随着速度的增加,探测概率逐渐增大,光子波形变窄,峰值前移;目标的平动速度大于 35 m/s 时,随着平动速度的增加,探测概率逐渐降低,光子波形峰值强度明显降低,光子波形宽度无明显变化.与平动小目标的光子测距相比,扩展目标不受目标平动的影响,扩展目标的回波光子数为 38.76,约为平动小目标的平均回波的 10倍;光子事件数为 500,探测概率达到100%;扩展目标的光子波形质心位置前移 0.915 ns,距离漂移达到 13.73 cm ;扩展目标的激光回波很强,探测概率更高,产生的距离漂移也较大.可得:光子探测模式下,平动目标的探测概率明显降低;相较于扩展目标,平动目标的光子探测对发射激光脉冲能量要求更高.

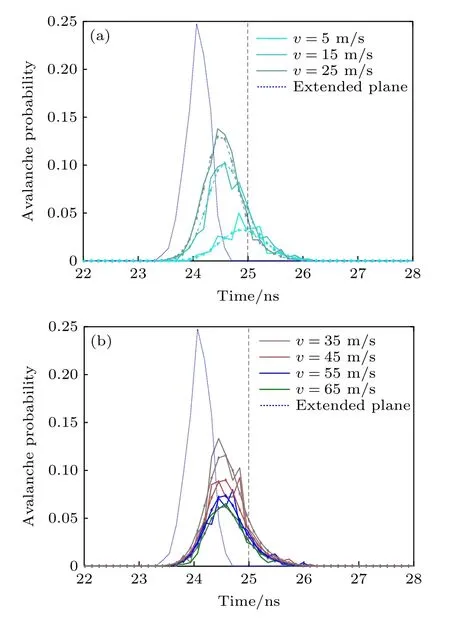
图6 不同平动速度的光子回波概率分布 (a) v=5—25 m/s;(b) v=35—65 m/sFig.6.Probability distribution of photon echo with different translational speed:(a) v=5 —25 m/s;(b) v=35—65 m/s.

为准确判断光子波形与目标平动速度的关系,光子探测平均回波光子数和光子事件数与目标平动速度的关系如图7 所示.

观察图7 可发现,速度为 25 m/s 时,回波光子数存在极大值.分析原因,目标平动速度为25 m/s时,目标在激光探测时间内运动了 2.5 m,恰好穿过光斑从光斑外运动到光斑边缘,确保在探测时间内的平均总回波强度最大;随着平动速度的进一步增加,在 2.5 m 后的回波强度会逐渐降低,使得整个探测时间的平均回波光子数降低,探测概率随着回波光子数的降低而减少,导致光子事件数逐渐变小.在探测时间内,平动目标未穿过激光光斑时,探测到的光子事件数随着速度的增加而增大,探测概率增大;穿过激光光斑后,探测概率降低,探测到的光子事件数逐渐降低.综上,平均回波光子数与光子事件数与目标在激光光斑内的留滞时间呈正相关.

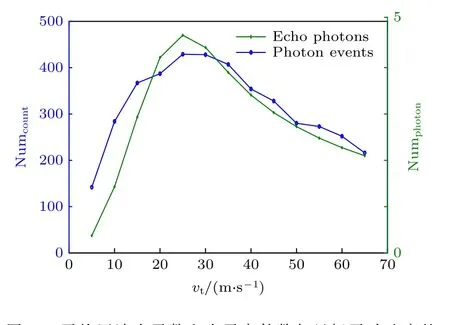
图7 平均回波光子数和光子事件数与目标平动速度的关系Fig.7.The relationship between the average number of echo photons,the number of photon events and the speed of target.

为进一步分析目标平动速度对光子测距性能的影响,其距离漂移与目标平动速度的关系如图8所示.

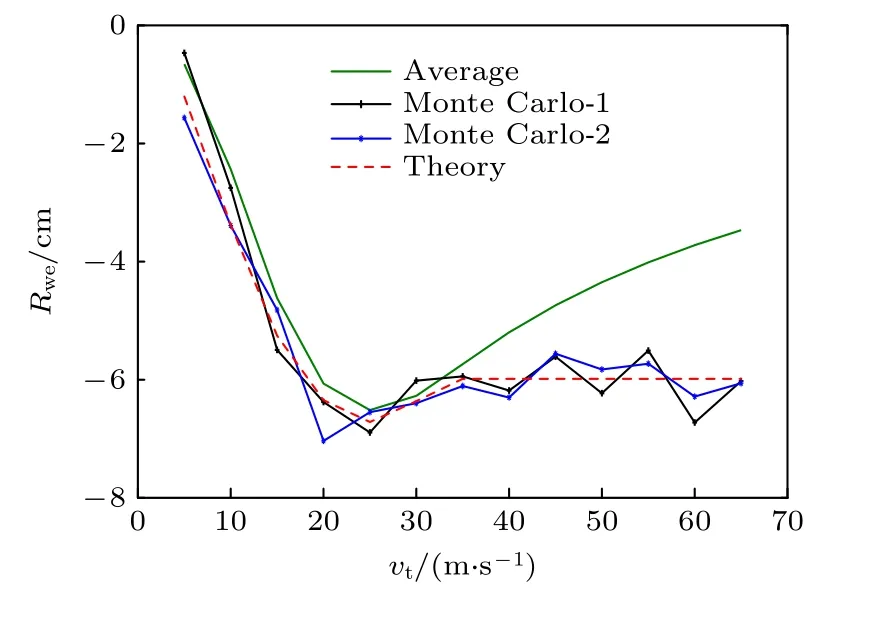
图8 距离漂移与目标平动速度的关系Fig.8.The relationship between the range walk error and target translational speed.

由图8 可知,蒙特卡洛仿真得到的两次随机结果都分布在理论计算的结果附近,仿真结果和理论计算都较为准确.速度为 25 m/s 时,距离漂移最大,值为 6.72 cm;当速度大于 35 m/s 后,距离理论得到的距离漂移稳定不变,值为 5.99 cm ;扩展目标的距离漂移为 13.73 cm,约为平动目标最大距离漂移的2倍.通过比较不难得到,平动小目标的回波光子数为扩展目标的 1/10倍,距离漂移却为其1/2 倍.从图8 可以发现,相较于图中的绿色实线,平动目标的距离漂移普遍较大,两者相差最大为 2.52 cm ;尤其当速度大于 35 m/s 后,平均激光回波对应的平均光子波形距离漂移一直降低,而仿真结果几乎保持不变,分析原因,这是由于激光回波和光子波形的产生机理不同导致的:1)光子波形为光子事件到达时间的累计统计直方图,速度较大时,无回波信号的发射脉冲不会影响其分布;2)平均激光回波是对所有发射激光回波的平均,速度较大时,统计次数一定,总回波信号强度降低,平均回波强度降低,此时计算得到的距离漂移与实际光子测距产生的距离漂移差距较大.综上,随着平动速度的增加,以出光斑为界,距离漂移先增大后保持稳定;平动目标的最大距离漂移约为扩展目标的1/2 倍.

4 结论

本文建立了运动目标的光子探测回波概率分布模型,结合发射激光重复频率、单光子探测器的死时间和系统单次探测时间周期等时间因素,给出了光子探测回波概率分布蒙特卡洛仿真模型.该模型亦可推广至其他形状、材质、姿态和运动目标形式的目标.通过与文献中的实验结果对比,验证了蒙特卡洛模型的正确性.仿真分析了平动小目标的激光回波和光子回波概率分布的变化特征,并与扩展目标结果进行了对比;在此基础上,讨论了光子测距误差与目标平动速度的变化规律.结果表明:相较于扩展目标,平动小目标的光子探测概率明显降低,最大平均回波光子数为扩展目标的 1/10 倍,对发射激光脉冲能量的要求增高;目标尺度为1 m时,距离漂移在速度为 25 m/s时取到极大值 6.72 cm,为扩展目标的 1/2 倍;随着平动速度的增加,以出光斑为界,距离漂移先增大后保持稳定.本文的结论为后续的运动目标光子测距实验和误差分析提供了新的思路和理论分析基础,为运动目标的测距误差校正和测距性能提升提供了有力的信息支撑.进一步地,为光子计数激光雷达对运动目标的探测和信息的准确获取奠定了基础.