Sawtooth-like oscillations and steady states caused by the m/n = 2/1 double tearing mode

Wei ZHANG (张威), Zhiwei MA (马志为), Haowei ZHANG (张豪伟)and Xin WANG (王鑫)

Institute for Fusion Theory and Simulation, Department of Physics, Zhejiang University, Hangzhou 310027, People’s Republic of China

Abstract The sawtooth-like oscillations resulting from the m /n =2 /1double tearing mode (DTM) are numerically investigated through the three-dimensional, toroidal, nonlinear resistive-MHD code(CLT).We find that the nonlinear evolution of the m /n =2 /1DTM can lead to sawtooth-like oscillations, which are similar to those driven by the kink mode.The perpendicular thermal conductivity and the external heating rate can significantly alter the behaviors of the DTM driven sawtooth-like oscillations.With a high perpendicular thermal conductivity, the system quickly evolves into a steady state with m /n =2 /1magnetic islands and helical folw.However,with a low perpendicular thermal conductivity, the system tends to exhibit sawtooth-like oscillations.With a suffciiently high or low heating rate, the system exhibits sawtooth-like oscillations, while with an intermediate heating rate, the system quickly evolves into a steady state.At the steady state, there exist the non-axisymmetric magnetic feild and strong radial folw, and both are with helicity of m /n =2 /1.Like the steady state with m /n =1 /1radial folw,which is beneficial for preventing the helium ash accumulation in the core,the steady state with m /n =2 /1radial folw might also be a good candidate for the advanced steady state operations in future fusion reactors.We also fnid that the behaviors of the sawtooth-like oscillations are almost independent of tokamak geometry,which implies that the steady state with saturated m /n =2 /1islands might exist in different tokamaks.

Keywords: DTM, reversed magnetic shear, pressure crash, sawteeth, sawtooth, double tearing mode, steady state, advanced scenario

1.Introduction

Scenarios with internal transport barriers (ITBs) associated with reversed magnetic shear are designed as the advanced steady state operations in fusion reactors [1, 2].The reversed magnetic shear can suppress trapped electron modes [3] and ballooning modes and significantly improves energy confinement [3–6].However, severe magnetohydrodynamic (MHD)instabilities,often observed with the reversed magnetic shear in tokamaks, can significantly degrade the energy confinement.These MHD instabilities sometimes lead to periodical oscillations of the plasma pressure in the core region[7–11],which is similar to sawtooth oscillations(or sawteeth).Therefore,these periodic oscillations are named off-axis sawteeth and on-axis sawteeth [7], or continuous MHD activity [9].An off-axis sawtooth means that the pressure crash only takes place in the annular region, and the on-axis pressure keeps almost unchanged.While, during an on-axis sawtooth, the plasma pressure in the whole core region experiences fast and significant reduction.The mechanisms of the two kinds of pressure crashes are very similar, and both of them are related to the nonlinear evolution of them≥2 double tearing mode[12, 13].If the magnetic flux around the axis is not reconnected, it causes the off-axis sawtooth crash; and vice versa.

In the present work, our studies focus on the on-axis sawteeth.To avoid confusion with the m/n = 1 kink-driven sawtooth[14–18],we name on-axis sawteeth as sawtooth-like behaviors or sawtooth-like oscillations in the present paper.Although the linear and nonlinear evolutions [19–26], the nonlinearly explosive growth of DTM [27–36], and DTM suppression [37–44] have been intensively investigated, the periodic oscillations associated with DTMs(i.e.sawtooth-like oscillations) are rarely numerically investigated.

In the present work,we focus on the characteristics of the sawtooth-like oscillations, including the periods and the amplitudes of the oscillations, the typical pressure profiles,and flow patterns during the oscillations.We find that the behaviors of the sawtooth-like oscillations can be altered with different perpendicular thermal conductivities or heating rates.With a proper heating rate or high perpendicular thermal conductivity, the system quickly reaches a steady state with the non-axisymmetric magnetic field and strong radial flow, similar to the steady state driven by the kink instability[15].However, the dominant mode is DTM in the reversed magnetic shear configuration,while it is them/n=1 /1kink mode in a monotonous q configuration.The quasi-stationary state associated withm/n=2 /1DTM is also sawtooth-free and can avoid severe pressure crashes,which is similar to them/n=1 /1steady state.Meanwhile,the radial flow can help prevent helium ash accumulation in the core region and such a steady state might be necessary for advanced operations for future fusion reactors.

2.Numerical model

The resistive-MHD equations utilized in CLT [45, 46] are:

whereρ,v, p,B,J andE are the plasma density, the fluid velocity, the plasma pressure, the magnetic field, the current density, and the electric feild, respectively.Γ =5 /3is the ratio of specifci heat.In CLT, we use the electric feild as an intermediate variable for the purpose of keeping∇· B =0.The variables used in CLT are normalized as follows: x/a→x,t/tA→t,ρ/ρ00→ρ,p/(B020/μ0)→p,v/vA→v,J/(B00/μ0a)→J,B/B00→B,andE/(vAB00)→E,respectively.Whereais the minor radius,B00is the initial magnetic field at the magnetic axis,ρ00is the initial plasma density,is the Alfvén speed,andtA=a/vAis the Alfvén time.η,D,κ⊥,κ‖,H0anduare the resistivity,the diffusion coefficient, the perpendicular and parallel thermal conductivity, the heating rate, and the viscosity, respectively,which are normalized as follows:η/(μ0a2/tA)→η,D/ (a2/tA)→D,κ⊥/ (a2/tA)→κ⊥,κ∣∣/ (a2/tA)→κ∣∣,H0/ (a2/tA)→H0,andν/ (a2/tA)→ν.

Since the present work investigates the sawtooth-like oscillations, external heating sources are needed for continuing oscillations.For simplicity, we assume that all external heating sources are included in the last term in equation(2).Such an external source always heats the plasma towards a peak distribution of the plasma,and the heating rate is proportional toH.0Meanwhile, in Ohm’s law(equation (5)), we add a source term (-ηJ0), which acts as a current driving source so that the magnetic flux surfaces and the current profile can restore after each crash.

3.Simulation results

3.1.The sawtooth-like oscillations

In the present work,we utilize similar parameters from EAST,i.e.the minor radius0.45 m, the major radius 1.85 m, the elongation 1.9,the triangularity0.5,the toroidal field ～2.0 T,and the plasma current ～0.7 MA.Similar to that shown in[47],we choose a q profile with two q=2 resonant surfaces.The equilibrium pressure and safety factor profiles used in the present paper are shown in figure 1.The distance between the two q=2 resonant surfaces areΔr=0.35a.The equilibrium fields are derived from the NOVA code [48].The grids used in the simulations are256 ×32 ×256(R,φ,Z).The convergence studies have also been carried out with different time steps and spatial resolutions.

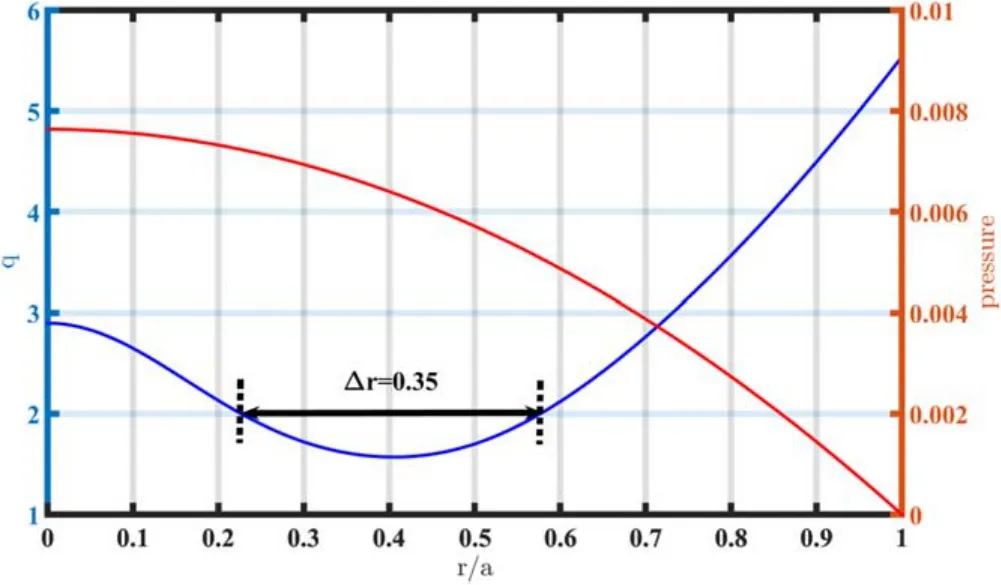
Figure 1.Initial safety factor and pressure profiles used in the simulations.

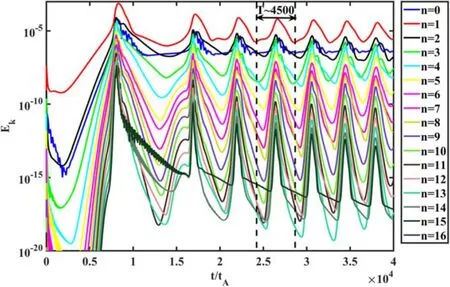
Figure 2.Evolution of the kinetic energy for different toroidal modes.It is evident that all modes experience periodic oscillations,and their periods are the same,T～4500t A.

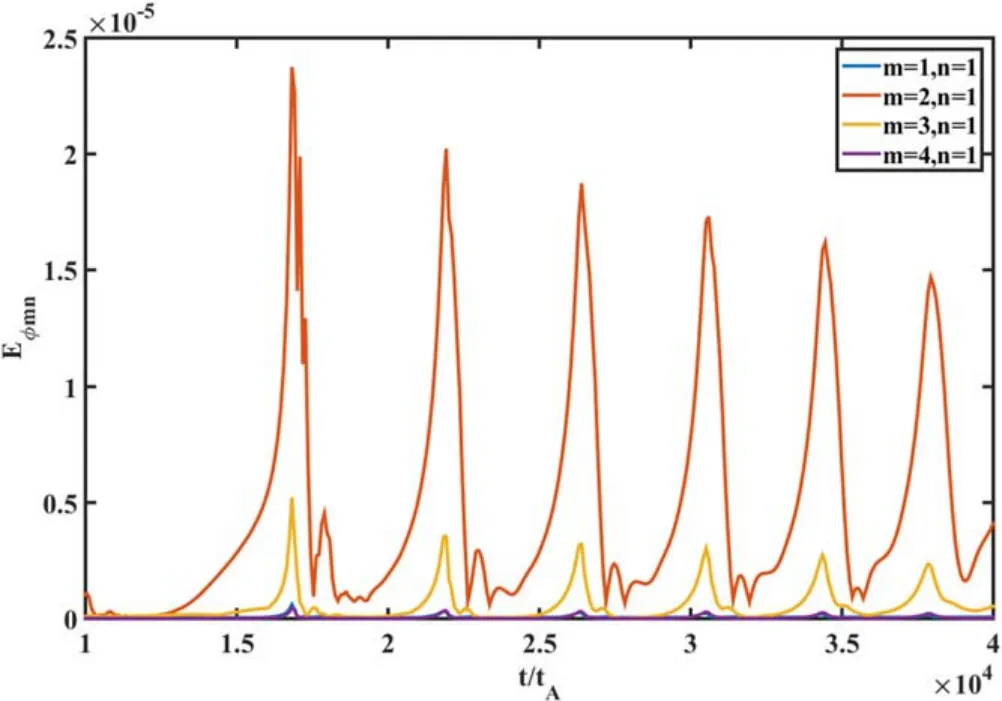
Figure 3.Evolution of the toroidal electric field Eφ mn.Since the modes with different mode numbers are located at different radii,we choose the maximum Eφ mnat each time step to indicate the amplitudes of the modes.The m /n =2 /1mode is the dominant one throughout the simulation.

The normalized diffusion parameters used in this subsection are chosen to beη= 3 ×10-6,D= 1 ×10-4,κ⊥= 3 ×10-6,κ∣∣= 5 ×10-2,H0= 3 ×10-6,andν= 3 ×10-5.The typical plasma parameters in EAST reversed magnetic shear discharge (e.g.EAST #71326 [47])aren0= 3 ×1019m-3,B0=2.0 T,and the Alfvén time istA～ 2 ×10-7s.The diffusion parameters in MKS areη=1.9 ×10-5Ωm,D=500 m2s-1,κ⊥=15 m2s-1,H0=15 m2s-1,andν=150 m2s-1,which is about two orders of magnitude larger than the realistic parameters.Since real tokamak parameters far exceed the present capability of the CLT code, we choose much larger resistivity and diffusion parameters for reducing the period of the sawtooth-like oscillations.Therefore, we are able to numerically investigate such sawtooth-like behaviors with limited computer resources.

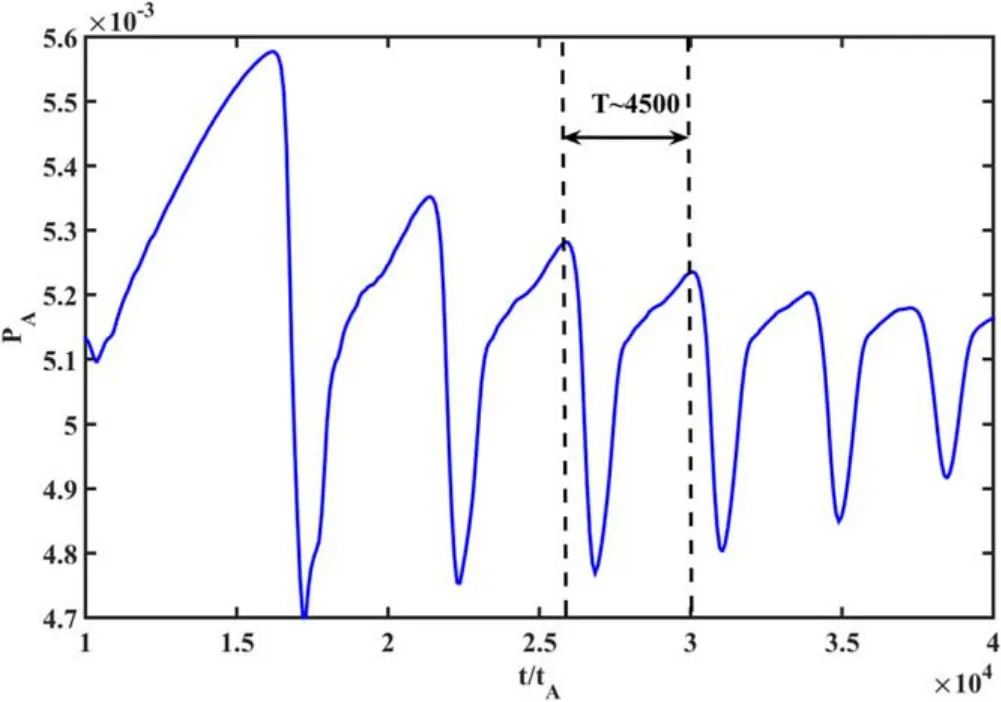
Figure 4.Evolution of the on-axis plasma pressure.It is evident that the on-axis plasma pressure also experiences periodical oscillations with the period T～4500t A.

The evolutions of the kinetic energy for different toroidal modes are shown in figure 2.It indicates that the kinetic energies for all toroidal modes experience periodic oscillations.The oscillation period of the kinetic energy is about 4500tA.We further decompose the n = 1 component with different poloidal mode numbers m.The evolution ofEφmnis shown in figure 3.The dominant mode is them/n=2 /1 mode, which confirms that them/n=2 /1mode drives the oscillations.Besides the kinetic energy, other characteristics such as the on-axis plasma pressure also exhibits periodical oscillations with the same periodT～4500tA,as shown in figure 4.The sawtooth period in the simulations is much shorter than that observed in the experiments(～100ms).The sawtooth period is mainly determined by the heating and the flux pump rates.However, such a long-time simulation far exceeds the capability of the CLT code.As a result, simulations are carried out with unrealistic parameters to partly explain experimental observations.As we can see, although the system has no q = 1 resonant surface, it still could experience periodical oscillations.The behavior is similar to sawteeth driven by them/n=1 /1resistive-kink mode, but the dominant mode is them/n=2 /1DTM.

The Poincare plots of magnetic field lines during one sawtooth cycle are shown in fgiure 5, which confirms that them/n=2 /1DTM drives the sawtooth-like oscillations.Att=25054tA(fgiure 5(a)), largem/n=2 /1magnetic islands at the two q=2 resonant surfaces form,which is the precursor of the pressure crash.Note that the plasma in the inner islands is hot while it is cold in the outer islands.Just before the pressure crash (figures 5(b) and (c)), the inner islands are gradually expelled outward due to the inward expansion of the outer islands.Therefore, the hot plasma core finally squeezes out from the core region (figure 5(d)), which is one of the basic features of the on-axis pressure crash.After the severe pressure crashes, the external heating and magnetic pump in equations (2) and (5) become dominant, the system gradually recovers(figure 5(d)),and a new cycle begins(figures 5(e)and(f)).The flux surface cannot be wholly reconstructed to its equilibrium during the recovery phase, and nonnegligible 2/1 islands exist even at the beginning of one cycle.

We have plotted the contour plots of the plasma pressure with the flow pattern at the same moments in figure 5.During the DTM precursor (figure 6(a)), the plasma pressure profile becomes flattened inside the islands, and the plasma flows generated by the reconnection process are weak.Just before the pressure crash (figures 6(b) and (c)), an elongated hot plasma region forms due to the inward expansion of the outer islands, as shown in figures 5(b) and (c).Meanwhile, strong radial flow is generated along this hot plasma region.The radial flow quickly transfers the hot plasma from the core to the outer region,leading to the on-axis pressure crash.Due to external heating, the plasma pressure at the axis starts to recover after the radial flow dissipates.

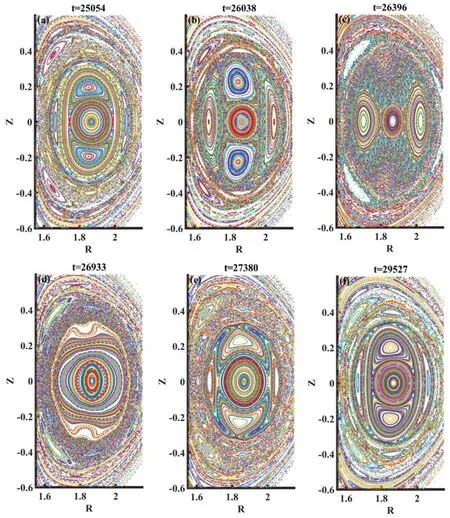
Figure 5.Poincaré plots of the magnetic field lines during one sawtooth cycle.

3.2.The sawtooth-like oscillations and the steady state

As shown in our previous studies, the plasma parameters(such as the viscosity) can significantly influence the kinkdriven sawtooth’s behaviors [15].The system can even achieve a steady state with a saturated m /n =1 /1magnetic island with a low viscosity.At a steady state, the sawtoothfree system can avoid severe pressure crashes.As a result, it might be necessary for tokamak operations [49].Although a steady state with a m /n =1 /1magnetic island has been widely investigated, the steady state driven by the DTM has rarely been discussed in the literature.

In this subsection, we keep the heating rate the same as the perpendicular diffusion rate(i.e.κ⊥=H0),and scan from κ⊥=H0= 1 ×10-6toκ⊥=H0= 3 ×10-5.As shown in figure 7, the behaviors of the sawtooth-like oscillations are significantly different—the amplitude of the pressure crash increases with increasingκ⊥=H0.Forκ⊥=H0= 1 ×10-6,the amplitude of the pressure crash is only about3%, while forκ⊥=H0=3×10-5,it is more than 20%.With alow heating rate, the system is weakly heated before the next crash.As a result,the amplitude of the pressure crash is small.

Interestingly, the on-axis pressure quickly reaches a steady state withκ⊥=H0= 3 ×10-5as shown in figure 7,which can also be seen from the evolution of kinetic energy(figure 8).The system quickly reaches a steady state after several cycles, and all the modes have kept unchanged since then.As one can see,these behaviors are similar to the steady state with the m /n =1 /1magnetic island.However, as shown in figures 9 and 10, the system at the steady state has saturated m /n =2 /1magnetic islands and plasma flow,which is different from the steady state with the m /n =1 /1 magnetic island.

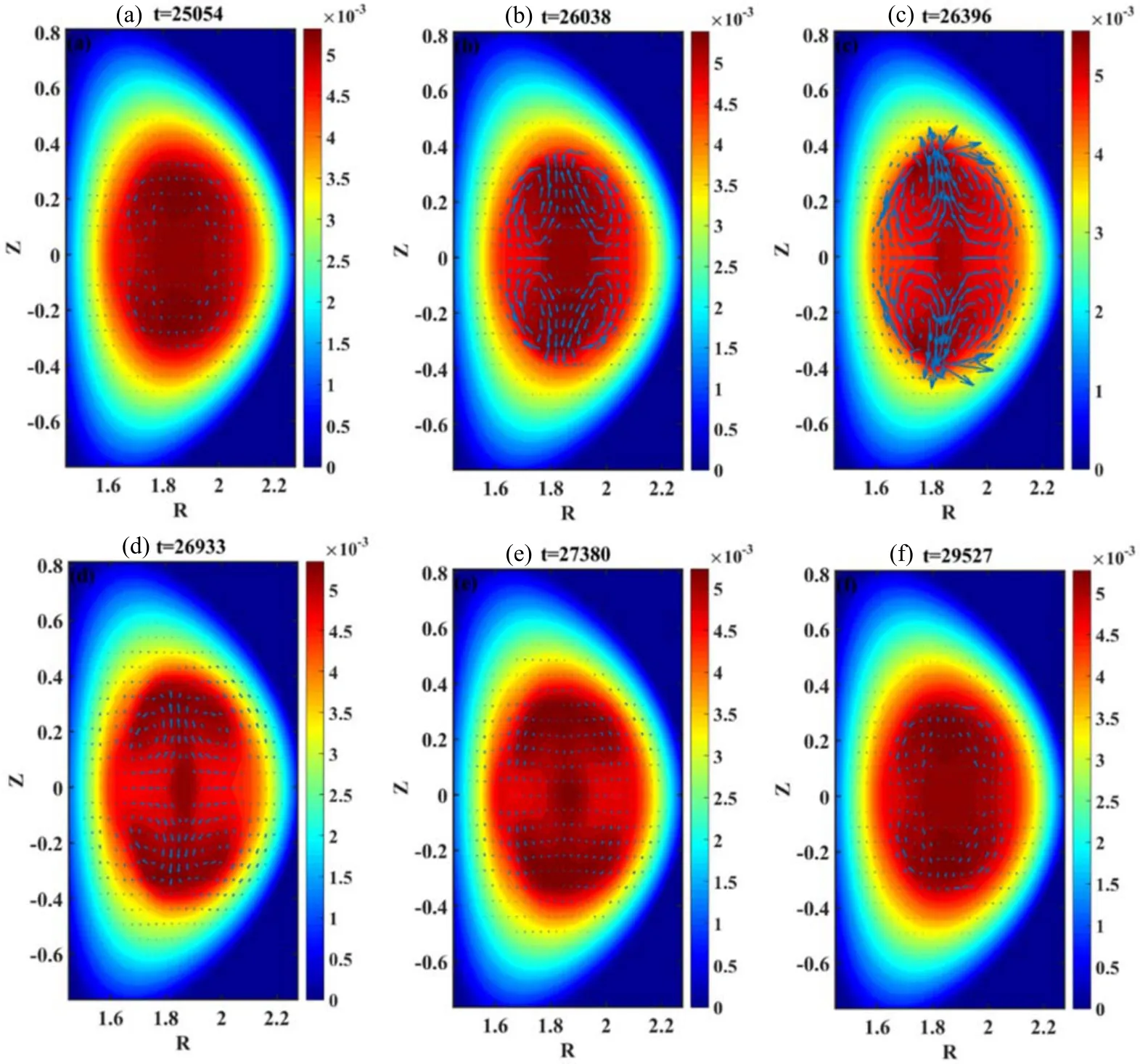
Figure 6.Contour plots of the plasma pressure with the flow patterns at the same moments in figure 5.The vector length in each figure has been normalized by the maximum value in figure 6(c).

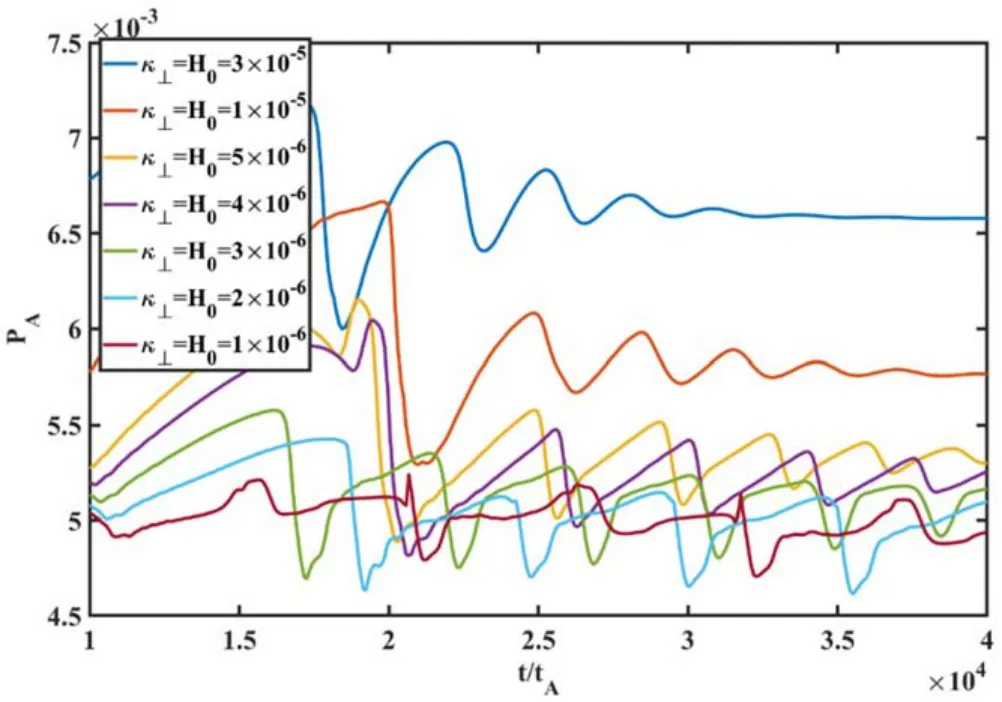
Figure 7.Evolutions of the on-axis plasma pressure with differentκ⊥ =H0 .

As discussed by many previous studies [50], the sawtooth-free steady state can avoid the pressure crash and prevent impurity accumulations in the core region since the radial flow carries both plasma and impurity from the core to the outer region.It implies that the steady state with the m /n =2 /1DTM might also be a proper candidate for the high confinement operation.

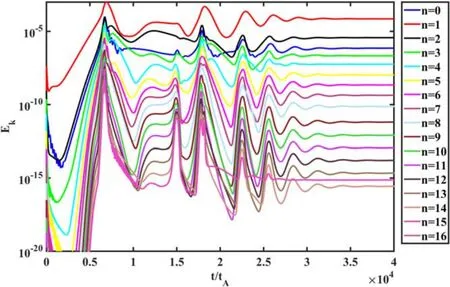
Figure 8.Kinetic energy evolution of the different toroidal mode numbers with== 3 ×The system reaches a steady state aftert～

3.3.The influence of the perpendicular thermal conductivity and the heating rate on the sawtooth-like oscillations

As shown in section 3.2, the behaviors of the sawtooth-like oscillations are sensitive to the perpendicular thermal conductivity and the heating rate.However, it is still unclear which parameter is the dominant one because we assumeκ⊥=H0for simplification.In this subsection, we will investigate the influence of the two parameters separately.

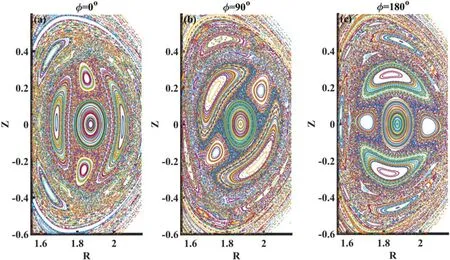
Figure 9.Poincaré plots of magnetic field lines at the steady state atφ =0 o,φ =90 o,andφ =180oin the EAST geometry.

Figure 10.Flow patterns and pressure profiles at the steady state atφ =0 o,φ =90 o,andφ =180oin the EAST geometry.

To study the influence of the perpendicular thermal conductivity,wescanfromκ⊥= 1 ×10-6toκ⊥= 3 ×10-5,and keepH0= 3 ×10-6.As shown in figure 11, the perpendicular thermal conductivity could largely alter the behaviors of the sawtooth-like oscillations.For example, the total kinetic energy quickly saturates, and the system reaches a steady state withκ⊥= 3 ×10-5,while,withκ⊥= 1 ×10-6,the system exhibits good periodicity.The evolutions of the on-axis plasma pressurefor the fixed heating rate (H0= 3 ×10-6) with different perpendicular thermal conductivities are shown in figure 12, clearly indicating that the system is more easily evolving into the steady state with a high perpendicular thermal conductivity.

Figure11.Evolutions of the total kinetic energyfor the fixed heating rate (=3 ×) with different perpendicular thermal conductivities.

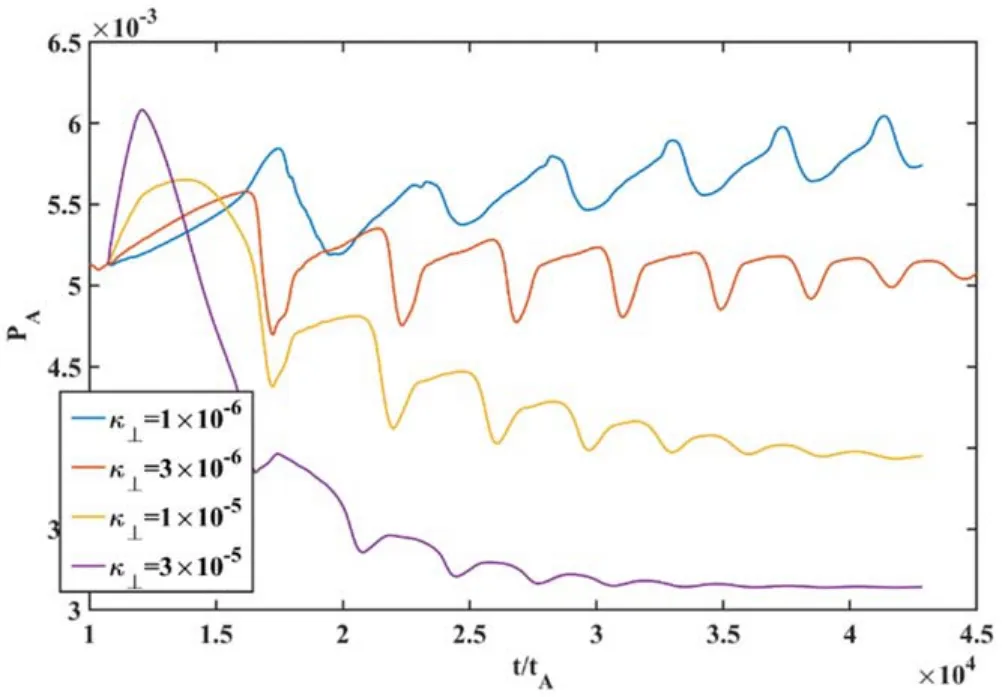
Figure 12.Evolutions of the on-axis plasma pressure for the fixed heating rate with different perpendicular thermal conductivities.

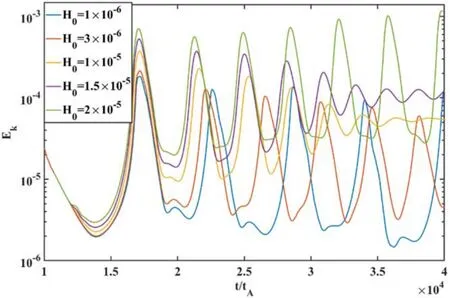
Figure 13.Evolutions of the total kinetic energy for the fixedperpendicular thermal conductivity with different heating rates.

Similarly,to investigate the influence of the heating rate,we scan fromH0= 1 ×10-6toH0= 2 ×10-5with the fixed conductivityκ⊥= 3 ×10-6.The evolutions of the total kinetic energy for the fixed perpendicular thermal conductivitywith different heating rates are shown in figure 13.We find that the system can evolve to a steady state with a moderate heating rate.However, the system exhibits a sawtooth-like oscillation with a relatively high or low heating rate.Such tendency can also be seen from the evolutions of the on-axis plasma pressure, as shown in figure 14.

3.4.The sawtooth-like oscillations in the ITER geometry

In this subsection,we utilize similar parameters from ITER to investigate the sawtooth-like behaviors in ITER.The major radius R0=6.20 m,the minor radiusa =2.0 m,the elongation E=1.7, the triangularityσ =0.3.Since we only focus on the internal instabilities, the simulation boundary is chosen to be the last closed surface in the present work.The initial q and pressure profiles versus the minor radius are the same with figure 1, and other normalized parameters are also kept the same as in section 3.2.With the ITER geometry,the on-axis plasma pressure evolutions with differentκ⊥=H0are qualitatively the same as section 3.1.As shown in figure 15,the system exhibits sawtooth-like oscillations with κ⊥=H0= 3 ×10-6,while,it quickly reaches a steady state withκ⊥=H0= 3 ×10-5.Similarly, strong radial flow and large m /n =2 /1magnetic islands exist at the steady state(figures 16 and 17).

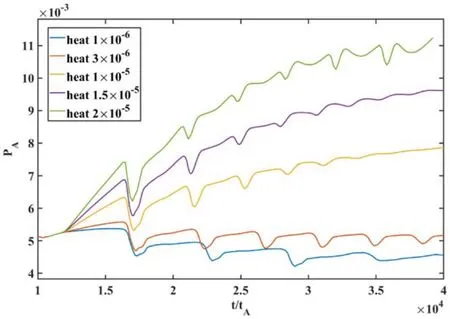
Figure 14.Evolutions of the on-axis plasma pressure for the fixed perpendicular thermal conductivity with different heating rates.

Figure 15.Evolutions of the on-axis plasma pressure with the differentin ITER geometry simulations.

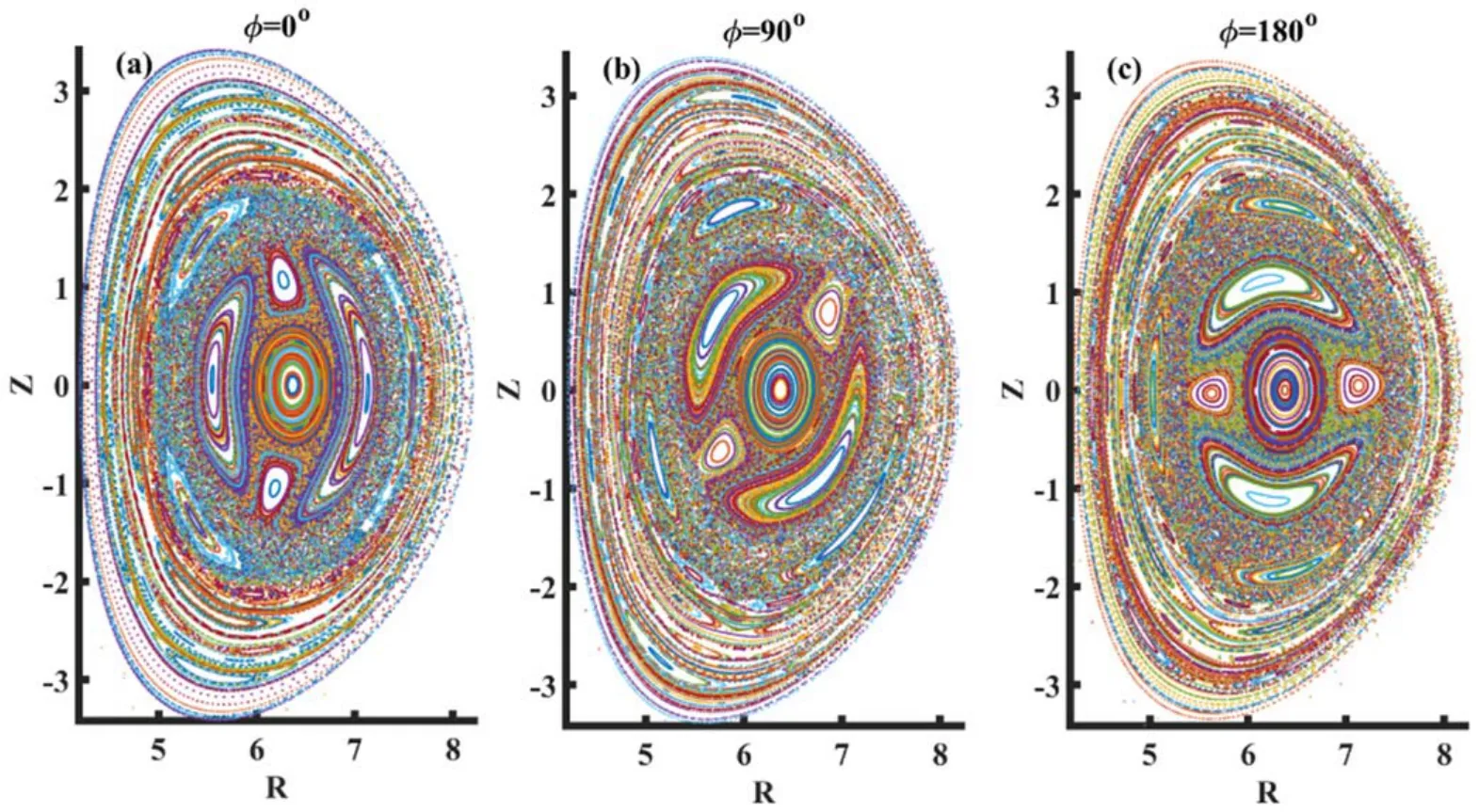
Figure 16.Poincaré plots of magnetic field lines at the steady state atφ =0 o,φ =90 o,andφ =180oin ITER geometry.

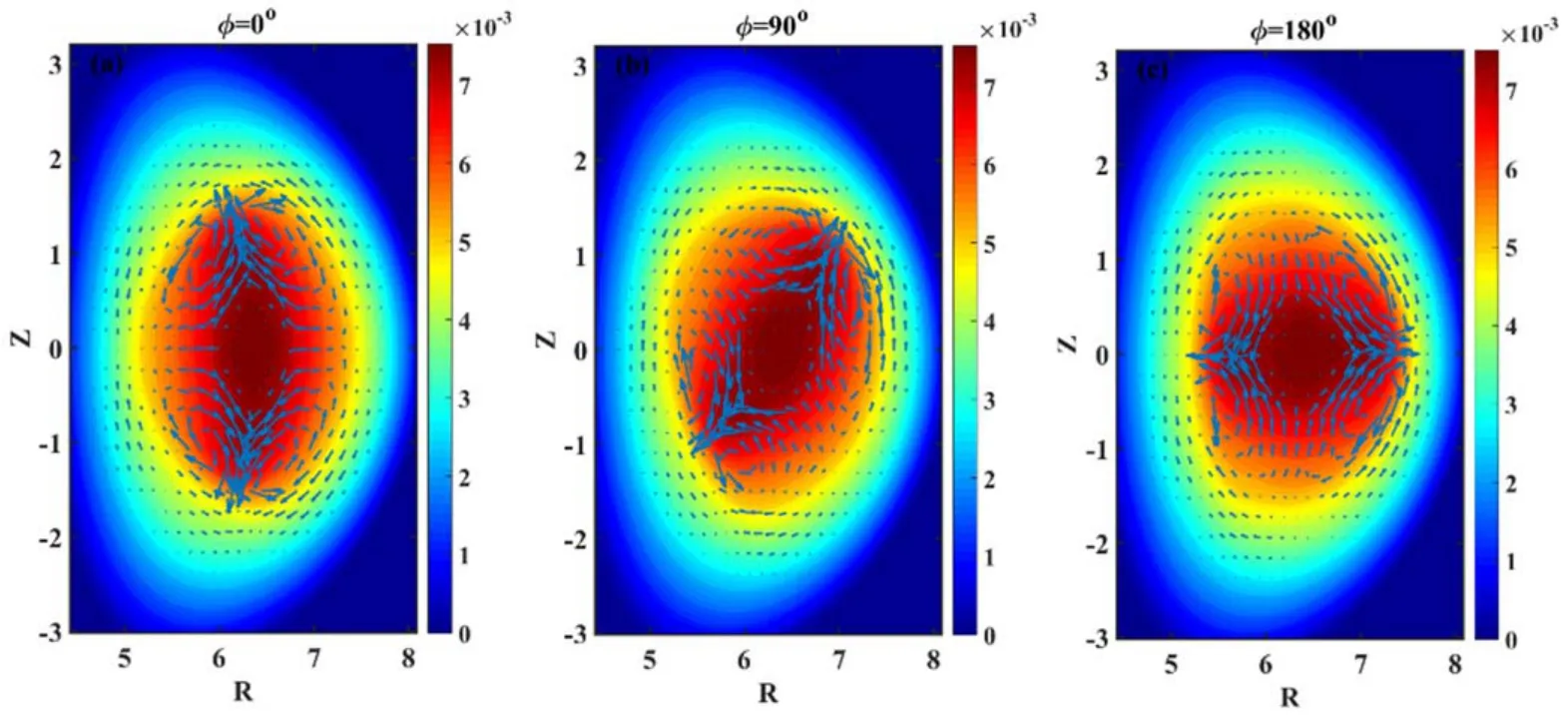
Figure 17.Flow patterns and pressure profiles at the steady state atφ =0 o,φ =90 o,andφ =180oin ITER geometry.

We have also carried out simulations to investigate the sawtooth-like oscillations with different tokamak geometries(the ASDEX-U and TFTR).Since the results are qualitatively the same,we do not present these similar results in the present work.These studies indicate that different tokamak geometries only weakly affect the behaviors of the sawtooth-like oscillations.

4.Discussions and conclusions

The sawtooth-like oscillations driven by the m /n =2 /1 DTM are numerically investigated through the three-dimensional,toroidal,nonlinear resistive-MHD code(CLT).Similar to the kink-driven sawtooth oscillations, both the kinetic energy and the plasma pressure oscillate with the same period.Them/n=2 /1DTM is dominant throughout the oscillation periods.

We have systematically investigated the influence of the heating rateH0and the perpendicular thermal conductivity on the behaviors of the sawtooth-like oscillations.We find that,with a higher perpendicular thermal conductivity, the system is more easily evolved into a steady state; however, with a low perpendicular thermal conductivity, the system tends to exhibit sawtooth-like oscillations.We also find that the behaviors of the sawtooth-like oscillations can be altered by imposing different heating rates.With a relatively high or low heating rate, the system exhibits sawtooth-like oscillations,and the system quickly evolves into a steady state with an intermediate heating rate.

The system has a non-axisymmetric magnetic field and a strong radial flow at the steady state, which is similar to the steady state observed in the kink-driven sawtooth oscillations[15].The helicity of the saturated magnetic islands and the plasma flow ism/n=2 /1for the DTM dominant steady state, while it ism/n=1 /1for the resistive kink driving steady state.As we know,the radial flow can help to expel the helium ash and thus prevent helium ash from accumulating in the hot core.Even more, there is no severe pressure crashes naturally for the sawtooth-free steady state.Similar to the steady state with them/n=1 /1magnetic island, the steady state with DTM is also beneficial to preventing helium ash accumulation in the core and avoiding severe crashes.It implies that such a scenario might be a good candidate for future fusion reactors.We have also carried out systematical simulations to investigate the sawtooth-like oscillations with different tokamak geometries.We find that the behaviors of the sawtooth-like oscillations and the steady state are qualitatively the same in different tokamak geometries.Therefore,we believe that the steady state with DTM might widely exist in present tokamaks.

The diffusion parameters and heating sources used in the present work are not real tokamak parameters.Using real tokamak parameters far exceeds the capability of the CLT code.With much larger resistivity and diffusion parameters,we can shorten the periods of the sawtooth-like oscillations so that we can numerically investigate such sawtooth-like behaviors.Although such studies leave some uncertainty,they still can give insight into the mechanism for the sawtooth-like oscillations.We are now working with the EAST team to validate our simulation results presented in this paper.Detailed comparisons and discussions with EAST’s data will be presented in the near future.

Acknowledgments

This work is supported by National MCF Energy R&D Program of China (Nos.2019YFE03090500 and 2019YFE03030004),National Natural Science Foundation of China(Nos.12005185,11775188 and 11835010), Fundamental Research Fund for Chinese Central Universities(No.2021FZZX003-03-02).

ORCID iDs