Comparison of double layer in argon helicon plasma and magnetized DC discharge plasma

Yueqing WANG (王玥晴), Ruilin CUI (崔瑞林), Ruoyu HAN (韩若愚),Feng HE (何锋), Tianliang ZHANG (张天亮), Jinsong MIAO (缪劲松) and Jiting OUYANG (欧阳吉庭)

School of Physics, Beijing Institute of Technology, Beijing 100081, People’s Republic of China

Abstract We present in this paper the comparison of an electric double layer(DL)in argon helicon plasma and magnetized direct current(DC)discharge plasma.DL in high-density argon helicon plasma of 13.56 MHz RF discharge was investigated experimentally by a floating electrostatic probe and local optical emission spectroscopy (LOES).The DL characteristics at different operating parameters, including RF power (300–1500 W), tube diameter (8–60 mm), and external magnetic field(0–300 G),were measured.For comparison,DL in magnetized plasma channel of a DC discharge under different conditions was also measured experimentally.The results show that in both cases,DL appears in a divergent magnetic field where the magnetic field gradient is the largest and when the plasma density is sufficiently high.DL strength (or potential drop of DL)increases with the magnetic field in two different structures.It is suggested that the electric DL should be a common phenomenon in dense plasma under a gradient external magnetic field.DL in magnetized plasmas can be controlled properly by magnetic field structure and discharge mode (hence the plasma density).

Keywords: helicon plasma, magnetized plasma, double layer, diverging magnetic field,electrostatic probe, OES

1.Introduction

An electric double layer (DL) consists of a positive and negative Debye sheath, connecting two quasi-neutral regions of the plasma which sustain a large potential jump, i.e., an electric field.Because of its thinness, DL is observed as a jump in the profile of electric potential and plasma density[1].DL can accelerate ions in the plasma plume, and the ion beam will further generate thrust, resulting in the DL acceleration effect of the plasmas [2–4].In 1929, Langmuir firstly proposed the concept of DL [5], and later Hairapetian et al found a DL without current[6].In 2003,Charles and Boswell first reported the formation of a current-free DL(CFDL)near the interphase of a helicon source and a larger diffusion chamber,and related the presence of a supersonic ion beam to the jump in electric potential across the CFDL [7–9].This research attracted great attention since it was suggested that the CFDL in an expanding plasma could be the basis of an enhanced type of space plasma thruster,hereinafter referred to as the Helicon Double Layer Thruster(HDLT)[10].This new type of thruster has advantages of electrodeless ablation,long life, high ionization efficiency, and large specific impulse[11–13].Although the efficiency of helicon thrusters was controversial recently [14, 15], the DL phenomenon is an interesting issue to deal with, at least in a physical manner such as the characteristics and formation mechanism.

Up to now, there have been two main considerations of DL formation in helicon plasma.Sun, Chen, Rao et al[16–18] suggested that DL is generated at the magnetic field gradient.Sun et al used non-perturbing laser-induced fluorescence to measure ion current.They confirmed that DL is in the region of maximum magnetic field gradient [16].Chen proposed that the DL is caused by the instability of sheath.The divergent magnetic field lines cause ions to accelerate and produce DL transitions.He also believed that the process would stop when the energy runs out [17].Rao et al used a two-dimensional (2D) simulation to prove that magnetized electrons diverge along the magnetic field lines,while unmagnetized ions flow directly downstream,forming a radial electric field structure [18].In contrast, Byhring and Ghosh et al [19, 20] thought that DL was formed only when the maximum magnetic field gradient coincides with the geometrical expansion.Byhring et al simultaneously measured the ion energy in the source and downstream areas of the antenna, showing that the potential drop of the plasma beam requires the presence of a magnetic field.Also, the potential drop is at the maximum magnetic field gradient and related to geometric expansion [19].Ghosh et al produced multiple DLs by creating a tangential magnetic field.They believed that both geometric expansion and magnetic field divergence must be available[20].Nevertheless,the effect of magnetic field gradient on DL in argon helicon plasma and other discharge structures has still not been clearly clarified in experiment.

In our previous work [21],it was demonstrated that DLs can be formed near the magnetic field gradient in wavecoupled (W-) mode in argon helicon plasma, and the magnetic field is one of the most important factors for DL.In this study,we try to confirm the decisive role of the gradient of the external magnetic field on the formation and structure of DL in discharge plasma.The effect of tube diameter on the strength of the DL was also verified.We will show that this kind of DL might also appear in some other discharge systems including DC discharge of plate-to-plate configuration.In this way,helpful comments will be provided for designing and controlling the HDLT.

2.Experimental platform and methods

2.1.Experimental setup

The experiment setup of helicon discharge is shown in figure 1(a);this has been used in our previous works[21–24].Briefly, the setup consists of a vacuum chamber and vacuum pump group, an RF power source and matching network, a couple of magnetic field coils, a helical antenna and water cooling.

The vacuum chamber is composed of a source chamber and diffusion chamber.For the helicon experiment,the source chamber is made up of quartz (figure 1), and is 450 mm in length and Φ=60 mm in diameter.The top of the quartz tube is sealed by a polytetrafluoroethylene (PTFE) end plate, and an inlet hole is provided for argon injection.The flow rate of argon is adjusted with a mass flowmeter (abbreviation MFC,Seven Star CS200).A 13.56 MHz RF power source is connected to a right helical antenna(155 mm in length,made of a hollow copper tube) through a self-optimizing matching network.

For comparison, a DC discharge experiment was also conducted, as shown in figure 1(b).The source chamber is replaced by a quartz tube 550 mm in length and Φ =80 mm in diameter.The electrode configuration is plate-to-plate,which replace the helical discharge system.The diameters of the cathode and anode plates (made of copper) are 60 and 50 mm, respectively.A DC power supply (HSPY-1500-002)is connected to the cathode to provide a DC voltage up to 600 V.The distance between the two electrodes is L=130 mm.A 5 mm wide gap is reserved in the middle of the anode plate.Through the gap, an electrostatic probe is placed under the cathode plate and grounded.

The diffusion chamber is made of stainless steel,500 mm in length and 330 mm in diameter.The vacuum pump system consists of mechanical and molecular pumps,which are fixed at the bottom of the diffusion chamber.The background pressure in this experiment is approximately 10-4Pa.The end of the quartz tube is noted as Z=0 (both in RF and DC discharge systems), and the positive direction is from the upstream source chamber to the downstream diffusion chamber.The magnetic field, helical antenna, RF power source, matching network, and vacuum pump set are equipped with a water-cooled heat-dissipation system which effectively reduces experimental errors caused by excessive temperature.

External magnetic field is produced and controlled by copper coils powered by two sets of DC power supplies.Figure 2(a) shows the 2D contour of the uniform magnetic field distribution.Figure 2(b) shows the uniform magnetic field and its first derivative.The maximum gradient of the magnetic field is at Z=0.Figure 2(c)is the 2D contour of the cusped magnetic field distribution.Figure 2(d) shows the cusped magnetic field and its first derivative, and the maximum gradient is at Z=-290 mm.

Figure 1.Experimental setup of (a) helicon plasma and (b) DC discharge plasma.

Figure 2.Distribution of external magnetic field at B0=150 G.(a)2D contour and(b)axial distribution of the uniform magnetic field for RF discharge.(c) 2D contour and (d) axial distribution of cusped magnetic field for DC discharge.

Figure 3.Schematics of LOES probe.

Figure 4.Schematic of floating electrostatic probe.

Figure 5.Axial profile of (a) plasma potential Vp, and (b) light intensity of 750.2 nm along the central axis.The discharge conditions are Φ =60 mm, B0=150 G, p=0.3 Pa, and P=1500 W.

Figure 6.Axial profile of (a) electron density Ne and (b) electron temperature Te along the central axis.The conditions are the same as in figure 5.

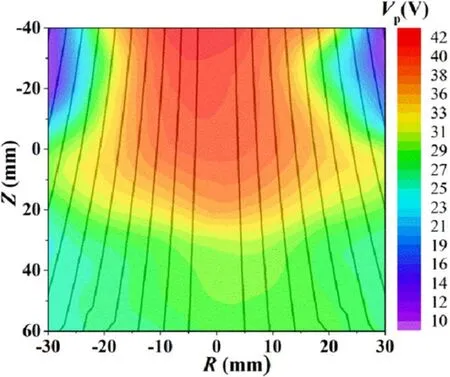
Figure 7.2D contours of plasma potential Vp and distribution of corresponding magnetic field lines.The conditions are the same as in figure 5.

2.2.Experimental method

The diagnostic methods used in this paper include a local optical emission spectroscopy (LOES) and a floating electrostatic probe.The electric probe and the optical fiber are fixed on a 2D movable platform,so that 2D profiles of plasma parameters can be obtained.The LOES probe is designed for spatial-resolved diagnosis of helicon plasma, as shown in figure 3.The probe body is made of alumina ceramic to withstand high temperature.The outer diameter is 5 mm and the length is 45 mm.There is a hole(or light well)in the tip to acquire the emission lights of local plasma (3 mm long), and there is an upper endplate above the light well to obstruct the light coming from the axial direction.Then the entered plasma,and hence the integrated line by LOES in the hole,is localized and spatially resolved when moving the probe.The spatial resolution is 3 mm.

In this work, we use the dual characteristic line ratio method [22] to obtain the electron temperature in helicon plasmas.For argon, 750.2 and 811.5 nm lines are selected in the experiment [22, 24]:

whereIArI811.5andIArI750.2are the emission intensities of the two different emission lines, [Ar] and [Arm] are the particle densities of the ground and metastable state,respectively,andare the rate coefficients for direct impact excitation of excited statesandfrom the ground state, and for impact excitation from the metastable state of the excited state, respecti vely.The density of argon metastables relates to that of electrons and neutral ground state atoms [25].While the density of neutral ground state particles satisfies the ideal gas state equation,the abovementioned rate coefficients can all be regarded as functions of electron temperature Te.At working pressure of 0.3 Pa, the evolution of the theoretical ratioIArI811.5/IArI750.2is a function of Te, referring to our previous work [22].Assuming the electron temperature Teis considered as a constant, then the electron density is proportional to the intensity of the emission spectrum.The intensity of the emission spectrum can directly indicate the electron density,

The value of k was determined via the comparison of calibration between the measured emission intensity from OES and the electron density from LP, and set as k=1.94×1014in this paper according to [22, 24].

The floating electrostatic probe [21], as shown in figure 4, is connected to an electrostatic voltmeter through a radio frequency filter circuit to obtain the floating potential Vf.The RF circuit can filter out AC signals of 13.56 and 27.12 MHz.

Compared with the traditional Langmuir probe, the floating electrostatic probe causes less disturbance to the plasma,and hence the measurement should be more accurate.However, since the mass of ions is much larger than that of electrons, and the speed of thermal motion is much smaller than that of electrons,the number of electrons gathered on the surface of the probe is much greater than the number of ions in unit time.An electron sheath will form on the surface of the probe caused by a negative charge.This electron sheath causes the value of the floating potential Vfto be negative relative to the plasma potential Vp.Therefore, the following corrections are required:

where kBis the Boltzmann constant, M is the ion mass, m is the electron mass,and e is the element charge.The corrected value can more intuitively and accurately characterize the characteristics of the plasma double layer.All the values of plasma potential presented in this article are corrected.

3.Results and discussion

3.1.DL in Ar helicon plasma

3.1.1.General characteristics.In Ar helicon plasma,DL can be observed in a quartz tube of 60 mm diameter under proper conditions,as shown by the axial distributions of Vpand light intensity in figure 5.

Generally, DL appears in W-mode and the RF power should be greater than 1000 W to ensure the W-mode.In the range from Z=0 to 30 mm,the potential drop is about 10 V,as shown in figure 5(a).Correspondingly, the emission intensity of the 750.2 nm line in figure 5(b) shows a similar axial distribution.

The measured plasma potential is an averaged value obtained through multiple measurements.The error bar is about ±5.0 V in the experiment.Although there were some errors of potential between each measurement (maximum of 5 V in this work), the charge trend of potential along the channel is just the same for all times.The averaged value can therefore represent well the plasma potential, which indicates really a DL in helicon plasma.

The distributions of electron temperature and electron density are given in figure 6.

In figure 6(a), the changing trend of electron density is consistent with the intensity of the 750.2 nm line.This is also consistent with the prediction in section 2.2 that the spectral line intensity is proportional to the electron density (or equation(2)).Considering the experimental error,the electric temperature is considered to be basically unchanged(figure 6(b)).This is basically consistent with the previous report [21].

The potential drop is not uniform on the whole radial section,as shown in figure 7 of 2D distribution in the(R,Z)plane for B0=150 G, p=0.3 Pa, and P=1500 W.The potential difference between two equipotential lines is 2 V.

It is seen that the plasma potential has maximum drop along the central axis (R=0), but becomes smaller away from the central line, or even reduces to zero near the tube boundary.The axial potential changes rapidly towards downstream, from Vp=39 V at Z=0 to 29 V at Z=30 mm.This potential drop (～10 V) across a short distance (～30 mm) along the central line shows the typical characteristics of traditional DL structures.Towards the tube wall, there is also a potential drop, forming a radial electric field, but the field strength is generally weaker than the axial DL.The equipotential lines are obviously curved outwards,showing a‘U-shaped’distribution[26]similar to the previous report [21].

3.1.2.Effect of external magnetic field.We noticed that the DL begins to appear when the magnetic field changes significantly, or the DL locates just at the gradient of magnetic field.To confirm the decisive role of the magnetic field on DL, we investigated the DL at different magnetic fields by changing the structure and the magnitude.

Figure 8(a) shows the axial potential distribution for p=0.3 Pa and P=1500 W at different magnetic fields,while figure 8(b)shows the series of coils moved 20 mm downwards plus the original potential without moving for comparison.

Figure 8.Axial potential distribution under magnetic fields of (a)different strengths and (b) different positions at B0=150 G.The conditions are Φ =60 mm, p=0.3 Pa, and P=1500 W.

Figure 9.Axial profiles of plasma potential Vp at different RF powers.The first derivative of the magnetic field is also plotted.The working conditions are Φ =60 mm, B0=150 G, and p=0.3 Pa.

Generally, a stronger magnetic field results in a larger potential drop, e.g., ΔVp～10 V at B0=150 G increases to ΔVp～12 V at B0=200 G and ΔVp～15 V at B0=300 G(see figure 9(a)).It is worth noting that no DL exists when the magnetic field strength B0=0,while the DL location follows the magnetic field structure, i.e., the DL moves down by 20 mm (i.e., the red line in figure 8(b)) compared with the original one(the black line in figure 8(b)).It can be concluded the DL always appears at the position where the magnetic field gradient is the largest.If the position of the magnetic field gradient changes, the DL will change accordingly.This means the divergent magnetic field contributes to the formation of DL structure in this case, although there were some other reasons to induce DL structure,e.g.,in expanding plasmas [27].

3.1.3.Influence of RF power.The potential drop and DL strength depend on the RF power, as shown in figure 9.

It is seen that at low RF powers, i.e., 300 (in E or CCP mode), 600, and 900 W (in H or ICP mode), the plasma potential basically changes smoothly.Above 1200 W (in W-mode), the potential drop increases significantly, from ΔVp～5 V at 1200 W to ～10 V at 1500 W.In our experimental conditions, DL is only observed in W-mode.It seems that there is a very small potential drop along the channel in E or H mode,but it is too small to act as DL.This might be because the axial electric field would be more easily fluctuated by the RF source.A small voltage drop was very hard to distinguish in experiments.We thought that a strong magnetic field(say,on the order of 0.1–1 T)might be helpful for observation of DL, but this needs to be verified in the future.

3.1.4.Influence of tube size.Figure 10 shows the plasma potential at different tube diameters.The working conditions were chosen to ensure the discharge is in W-mode, and the downstream plasma density of each tube diameter is nearly the same so that the comparison is reasonable.

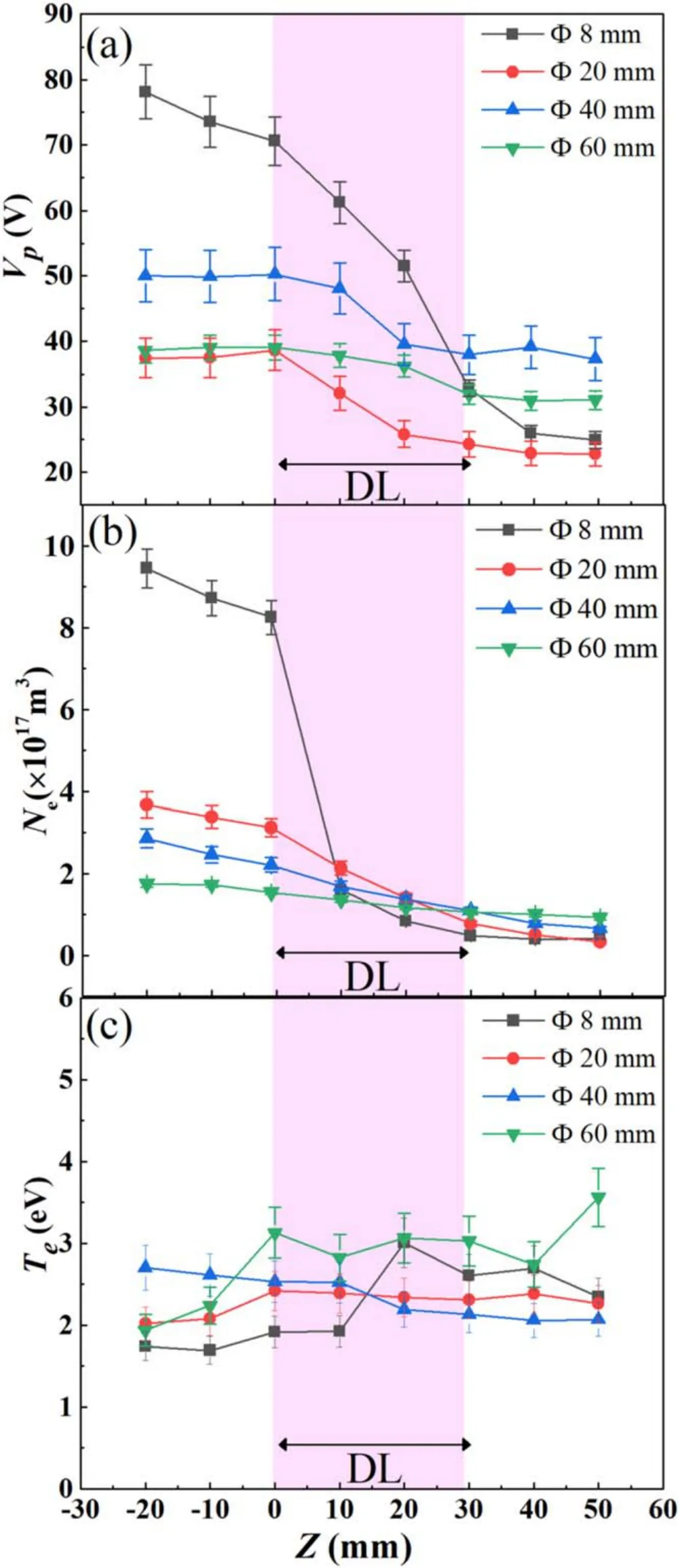
Figure 10.Axial profiles of (a) plasma potential Vp, (b) electron density Ne, and (c) electron temperature Te in tube of 8 to 60 mm at B0=150 G and p=0.3 Pa.The RF power is P=1500 W.

Figure 11.Change of (a) DL strength H and (b) density difference ΔNe between the upstream and downstream with tube diameter.

The potential distributions of different tube diameters are shown in figure 10(a), indicating that the plasma potential drop is correlated negatively with the tube diameter.The potential drop still occurs around the maximum magnetic field gradient.The changing trend of potential with axial distance is similar, but has a different slope.The DL strength is significantly greater in a smaller tube.The potential drop is ΔVp～45 V in an 8 mm tube, much larger than that in a 60 mm tube (ΔVp～10 V).During the discharge, the inner surface of tube will be charged due to the diffusion of electrons and ions, especially in a small tube.These wall charges would probably affect the space potential and hence the DL observation.But under the condition of nearly uniform plasma density in the diffusion region, the wall charge, if there are, should also uniform, and they will have no significant influence on the potential distribution.We,therefore, considered that the charge of plasma potential is mainly due to the space charges.

Correspondingly,the drop of plasma density Neafter DL is also larger in the smaller tube, as seen in figure 10(b).The Nein DL region decreases from 8.7×1017m-3to 8.4×1016m-3in 8 mm tube,while from 1.7×1017m-3to 9.3×1017m-3in 60 mm tube.The changing trend of electron density is similar to that of the plasma potential.However, the change of the Tein the measured DL region is not significant.This is also similar to the previous work[21].

In order to describe the DL more accurately, we introduced another parameter of DL strength H, defined asH=eΔVP/kBTelike that in[2].The relationship between the DL strength and the tube diameter is calculated and shown in figure 11.

It is found that when the downstream plasma density is the same,the DL strength is correlated with the tube size.For instance, at P=1500 W and Ne,down≈1016m-3, the calculated DL strength is H=4.6, 5.6, 7.0, and 20 in tube of 60,40,20,and 8 mm,respectively.The DL strength H and the electron density differenceΔNein the 60 mm tube are obviously lower than those in the other smaller tubes.

3.2.DL in magnetized DC discharge plasma

To further verify the effect of magnetic field gradient on DL,we measured the potential distribution in a magnetized plasma of DC discharge.We designed and placed a magnetic field coil to form a cusped field.When the output voltage of the DC source was 600 V and the working pressure was 50 Pa, DLs were found in the DC discharge plasma.

Figure 12 shows the axial distribution of the plasma floating potential and the first derivative of the magnetic field under different magnetic fields (0–400 G).

Figure 12.Distribution of plasma potential under different magnetic fields (0–400 G).The first derivative of magnetic field dBZ/dZ is also plotted.

Figure 13.Relationship between power densityσP and tube diameter.

As seen in figure 12, the plasma potential of the discharge region drops around the maximum gradient of the magnetic field (at Z=-290 mm).This is just similar to that in helicon plasmas.The DL position is not exactly at but around the maximum gradient of magnetic field in all cases.The averaged plasma density in the DC discharge channel is 1016–1017m-3.In this configuration,the local plasma density in front of DL (around Z=-310 mm) increases with the magnetic field, from 5×1016m-3at B=0 G to 1.5×1017m-3at B=400 G in this experiment.The potential drop occurs within a distance of 30 mm or less when the magnetic field changes significantly,showing the characteristics of DL.The potential drop increases with the field strength,from 4 V at 80 G to 10 V at 400 G.When there is no external magnetic field (or B0=0), the plasma potential is nearly constant and there is no potential drop or DL.

4.Discussions

We have confirmed that the DL surely appears in Ar helicon discharge and DC discharge plasmas in the gradient magnetic field.The results are summarized as follows.

(1) DL locates in the divergence area of magnetic field,and the DL position follows the magnetic field gradient.That is,when the position of the magnetic field gradient changes, DL changes its position accordingly.

(2) The DL strength increases with the magnetic field intensity increasing.

(3) Generally, the DL strength is positively correlated with the plasma density.A higher RF power or a smaller tube results in a larger DL strength in helicon discharge plasmas in W-mode.

From the above results,we suggested that DL should be a kind of charge separation in a gradient magnetic field due to the different behavior of magnetized electrons and nonmagnetized ions.The external magnetic field plays a decisive role in the production and controlling of DL.We then calculated the cyclotron radii of electron and ion to discuss the existence of DL.

When a charged particle moves in a magnetic field,it will be subject to the Lorentz force and make a cyclotron motion.In a helicon plasma, the cyclotron radius is

where me,iis the electron or ion mass, qe,iis electron or ion charge,and ve,iis the average cyclotron velocity of electron or ion expressed as

When B0=150 G and Te=2.5 eV, the calculated electron cyclotron radius is rce=0.37 mm,which is much smaller compared to the tube diameter of 8–60 mm; hence, electrons are confined and move around the magnetic field lines with a small radius.On the other hand,the mass of argon ions is much larger (approximately 6.63×10-26kg) than that of the electrons (approximately 9.11×10-31kg).The ion temperature Tiis close to the gas temperature Tg＜1000 K, or Ti≈Tg≈0.1 eV.Then the ion cyclotron radius can be calculated as rci=20.2 mm, which is on the same order as the tube diameter.The larger ratio of ion cyclotron radius to electron cyclotron radiusmeans that when the plasma diffuses from the upstream of higher density to the downstream of lower density, the ions are not magnetized in the “U-shaped” double-layer structure [26], but the electrons are highly magnetized.Therefore, when the magnetized electrons leave the source region, they will quickly follow the magnetic field lines but the unmagnetized ions will not move along the magnetic field lines.This different behavior between non-magnetized ions and highly magnetized electrons in the divergent magnetic field causes the separation of space charges, thereby generating a density gradient.The density gradient can give rise to a potential gradient that retards motion of the lighter plasma electrons but accelerates the more massive ions downstream [16].This is actually the feature of DL, showing an apparent potential drop in a short distance along the axis.

Under this mechanism, electric DL should not be a special phenomenon of helicon plasmas but a common one as long as there are a sufficient plasma density and a divergent magnetic field.Actually, acceleration of plasmas in some other thrusters like cusped field accelerator and/or magnetic nozzle is also achieved by this kind of DL in a gradient magnetic field.For example, the DC plate-to-plate discharge mentioned in this paper can also produce a similar DL structure.Furthermore, the magnetic nozzle constitutes the acceleration phase of the thruster.The divergent magnetic field lines guide the plasma flow to form an axial electric field,resulting in a potential drop similar to DL[28].Further,a cusped magnetic field is designed at the tube end,and under the influence of the magnetic field,a density gradient appears around the maximum magnetic field gradient to form a DL structure[20].These examples further support the importance of a gradient magnetic field to DL.

Considering tubes of 8 to 60 mm, when the discharge power is the same, it will lead to different power densitiesσP(σP=P/Stube,see fgiure 13) so that the upstream electron density is inconsistent(see figure 10(b))in different tubes.The electron density increases with the power density.When the downstream electron density is not much different,the density difference before and after the DL will decrease with the tube diameter(see figure 10(b)).That is,DL strength increases with the increase of power density in the tube.The power density(or plasma density)is an important factor that accounts for the difference of plasma potential in different tubes.

From this viewpoint, the DL is strongly relative to the plasma density,and hence it can be controlled by the tube size and the external magnetic field in helicon plasmas.This might provide a possible measure for designing HDLT.

5.Conclusions

In this work, we investigated the effects of operating parameters on the generation and characteristics of electric double layer in magnetized plasmas of argon helicon discharge and DC discharge by using floating electrostatic probe and LOES.Conclusive remarks are summarized as follows.

(1) In both helicon and DC discharge plasmas,double layers appear in the magnetized plasma channel around the diverging area of magnetic field where the magnetic field gradient is the largest.The strength of the double layers increases with the magnetic field intensity.Double layers have similar characteristics in different systems.

(2) The formation of the double layer is due to the different behavior of magnetized electrons and non-magnetized ions in the gradient magnetic field,which causes charge separation to form the potential drop.A gradient magnetic field is indispensable for the formation of double layers.There is a density gradient along the magnetic field line which forms a local accelerating electric field.A higher power density in a smaller tube is beneficial for the greater density gradient and hence the stronger double layer.

(3) The position and strength of the double layer can be controlled through the distribution of external magnetic field together with the input power density and appropriate discharge mode(hence the plasma density).This is helpful for HDLT design.

Acknowledgments

This work is supported by National Natural Science Foundation of China (No.11975047).

ORCID iDs