Non-universal Fermi polaron in quasi two-dimensional quantum gases

Yue-Ran Shi(石悦然) Jin-Ge Chen(陈金鸽) Kui-Yi Gao(高奎意) and Wei Zhang(张威)

1Department of Physics,Renmin University of China,Beijing 100872,China

2Beijing Academy of Quantum Information Sciences,Beijing 100193,China

3Beijing Key Laboratory of Opto-electronic Functional Materials and Micro-nano Devices,Renmin University of China,Beijing 100872,China

Keywords: Fermi gas,polaron problem,two-channel model

1. Introduction

The advent of two-dimensional Fermi gas has greatly renewed interest in the so-called polaron problem, which can be considered as the limiting case of a spin-imbalanced Fermi gas. It is of great importance to understand the fate of impurities as the interaction varies by tuning the Feshbach resonances. A natural expectation is that the system would undergo a transition and change its statistics as the impurity binds with background fermions.[33,34]Indeed, if the interaction is sufficiently weak, the impurity is dressed by the density fluctuation of the Fermi sea to form a polaron state.[35–37]With increasing attractive interaction, the impurity binds a background particle and forms a molecule.[38–41]Some previous studies suggest a transition between polaron and molecule states both theoretically[42–47]and experimentally,[48]while the critical interaction strength is obtained differently in different scenarios. Considering the transition takes place in the strongly interacting regime, the significant population of exited transversal modes of the harmonic potential[49–51]may lead to non-universal situation of this phase transition, and can provide the key to understand the discrepancy of the transition points between theoretical prediction and experimental outcome in this quasi-2D systems.

In this work, we investigate the quasi-2D polaron by using a variational approach and an effective two-channel model,in which the highly excited transversal levels are taken into account by introducing a phenomenological degree of freedom of dressed molecule.[49–51]We consider two different kinds of background fermions,6Li and40K,which have been well investigated in experiments.[30,48,52–54]Therefore three different mass ratiosη=m↓/m↑=1,6.64 and 1/6.64 are investigated.The main purpose of this work is to reveal the significant effects induced by the excited transversal levels of a quasi-2D geometry, such that the value of ¯hωz/EFcan strongly affect the position of the polaron–molecule transition. We numerically calculate the transition points for different mass ratios,and compare our results with previous experiments. We show the results of polaron energy, the wave function for the polaron state,and the effective mass are sensitively dependent on particle density and mass ratio. Furthermore, we discuss the excited repulsive polaron state in this system and find similar non-universal behavior.

2. Formalism

We consider an atomic Fermi gas trapped in aDdimensional harmonic potential with an isotropic trapping frequency ofωzin the transversal directions. Although in the following discussion we will focus on the quasi-2D case withD= 2 only, in this section we present a general formalism which is valid for both cases ofD=1 and 2. Besides,while it is possible to use a single-channel approach with a pseudopotential for a wide Feshbach resonance, for more general purposes,we adopt the conventional two-channel field theory which is valid for both wide and narrow Feshbach resonances.The Hamiltonian thus can be written as[50,55]

whereεkrepresents the two-dimensional dispersion.

This system has two possible ground states. For weak interaction,the ground state is expected to be a polaron with an approximate wave function[35]

Note that the Fermi sea here only containsN −1 spin-up fermions, thus the threshold energy would be different from the polaron state. Minimizing〈M(Q)|H −E|M(Q)〉, we obtain the molecule energy equation

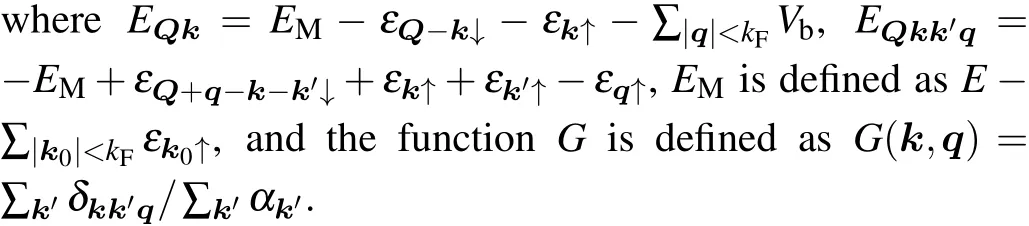
3. Results

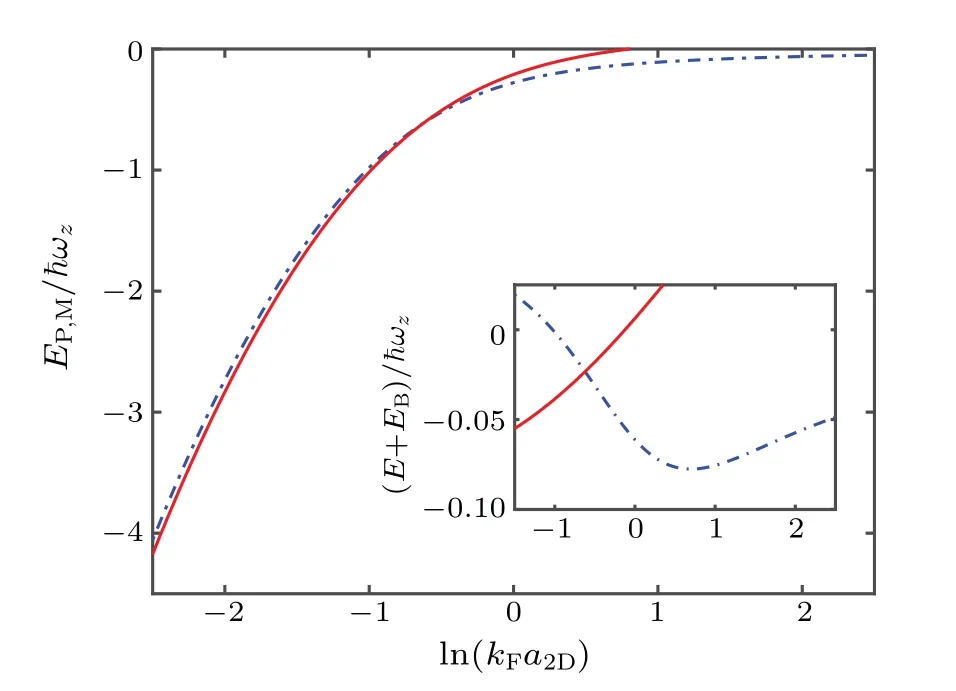
Fig.1. Energies of the attractive polaron(blue dotted-dashed line)and the molecule(red solid line)states with mass ratios η=1. Here we use the parameters for40K atoms and fix¯hωz/EF=7.85,which are adapted from the experiment configuration of Ref.[48]. The inset shows the result of E+EB,and the transition point resides at ln(kFa2D)=−0.6224.

Fig.2. The positions of transition point vary with ¯hωz/EF. The black square and red triangle lines represent the equal mass case, where the atoms are 6Li and 40K,respectively. From bottom to top the mass ratio is increasing.

The non-universal behavior is of potential importance when comparing theoretical results and experimental measurements. In many cold atom experiments such as Ref.[48],the quantum gases are trapped in a harmonic potential and the particle density varies from high to low by moving from the trap center to the edge. The response of the trapped gas under a global measurement is thus an average of all particles. Theoretical treatment can be performed within the local density approximation(LDA),under which the non-uniform system is considered as composed by segments with a local density fixed by the chemical potential with an on-site potential offset. The results shown in Fig.2 suggest that the density dependence has to be taken into account when quantitative analysis is sought.

Another non-trivial finding of Fig.2 is that the curves do not seem to saturate and remains non-universal for ¯hωz/EFas large as 40. This ratio corresponds to a very strong confinement and the quasi-2D condition should be satisfied quite well at the first glance. However, one must notice that in this system there is another energy scale characterizing the interaction energy,which can be chosen as the binding energy of the twobody bound state formed by the impurity and one background fermion. If the binding energy is comparable or even exceeds¯hωz, the excited levels of the transversal trapping potential would be significantly populated and the system remains nonuniversal. To better reveal this property, we further show the fraction of the bare impurity, the dressed molecule, and the two-dimensional fermions in the polaron wave function ansatz in Fig.3. The three components are defined as

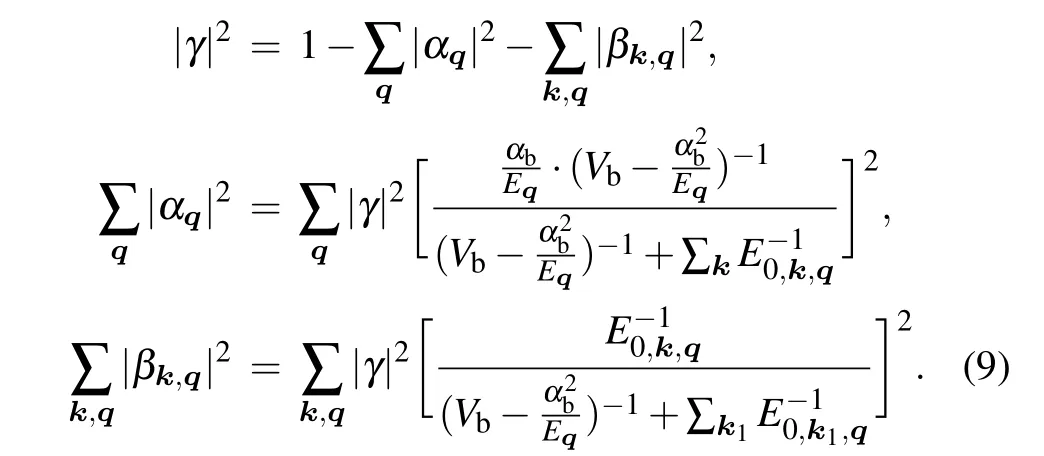
In the weakly interacting limit, the dominant part of polaron wave function is the bare impurity component|γ|2. In the intermediate and strong interaction regime, the dressed molecule fraction ∑|q||αq|2and fermionic contribution ∑|k|,|q||βq|2are both significant. Remind that the dressed molecule is a phenomenological description of the excited levels of the transversal trap, and thus this observation suggests that the system is not strictly 2D yet for the range of interaction considered.

Fig. 3. The fraction of the three components in polaron wave function for(a)η =1 and(b)η =6.64. Here the three lines for|γ|2 (black solid line),∑q|αq|2 (red dashed line) and ∑k,q|βq|2 (blue dotted-dashed line) represent the bare impurity,molecule and particle–hole excitation,respectively.

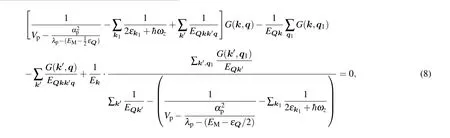
Next, we extend the discussion to finite center-of-mass momentum. The solution of Eqs.(7)and(8)at small but finite momentum|Q|≪k↑Fcan be expanded as

for both polaron and molecule states withm∗the effective mass. In Fig. 4, we show the effective mass for polaron and the inverse effective mass for molecule state. In the weakly interacting limit,the effective mass of the polaron state is the bare impurity massm∗≈m↓. With increasing interaction,the polaron state with zero center-of-mass momentum is always a metastable state with a positive effective mass. On the contrary,the molecule effective mass is negative for weak enough interaction, and the molecule solution withQ= 0 becomes unstable. In the strongly interacting regime,the effective mass for both the polaron and molecule states approach the same limiting valuem∗≈m↑+m↓.

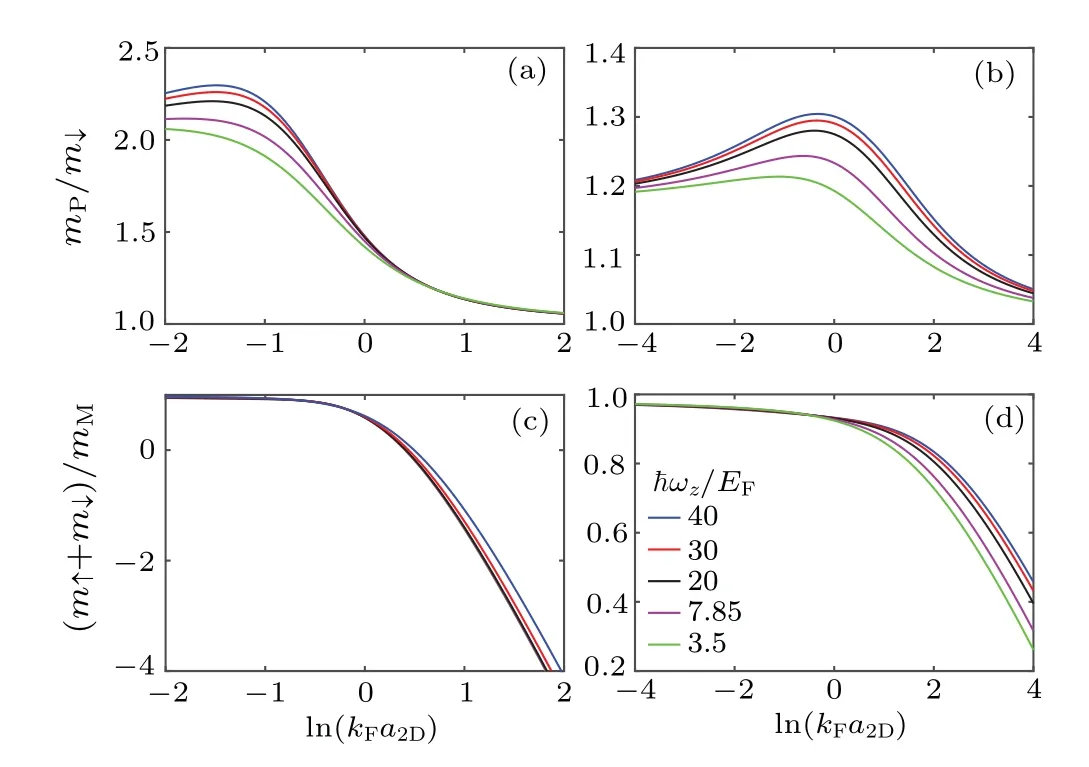
Fig.4. Effective mass of polaron state for(a)η =1,(b)η =6.64 and inverse effective mass of molecule state for (c) η =1, (d) η =6.64.The five lines from top to bottom represent ¯hωz/EF =40,30,20,7.85 and 3.5,respectively.

Finally,we investigate the properties of the repulsive polaron branch with a positive energy, which was recently realized in experiments in both three dimensions[57]and two dimensions.[58,59]We firstly write down the self-energy of a polaron state

In Fig. 5(a), we plot the spectral function as a function of energy and interaction strength ln(kFa2D) forQ=0 andη=1. There exist two branches where the spectral function is strongly peaked and labeled by bright yellow color. The lower branch corresponds to the attractive polaron state,which intersects with the molecule state(red dotted line)at the polaron–molecule transition. The thick upper branch labels the repulsive polaron,which is a fairly well defined excited state in the strongly interacting regime with a positive energy. As moving towards the weakly interacting regime, the repulsive polaron branch merges into the molecule–hole continuum. At small momenta,the energy of the two branches of polaron can also be calculated from

which is also displayed as blue dotted-dashed line in Fig.5(a).We also observe a non-universal density dependence of the repulsive polaron energy,as demonstrated in Figs.5(b)and 5(c)for mass ratioη=1 and 6.64,respectively.

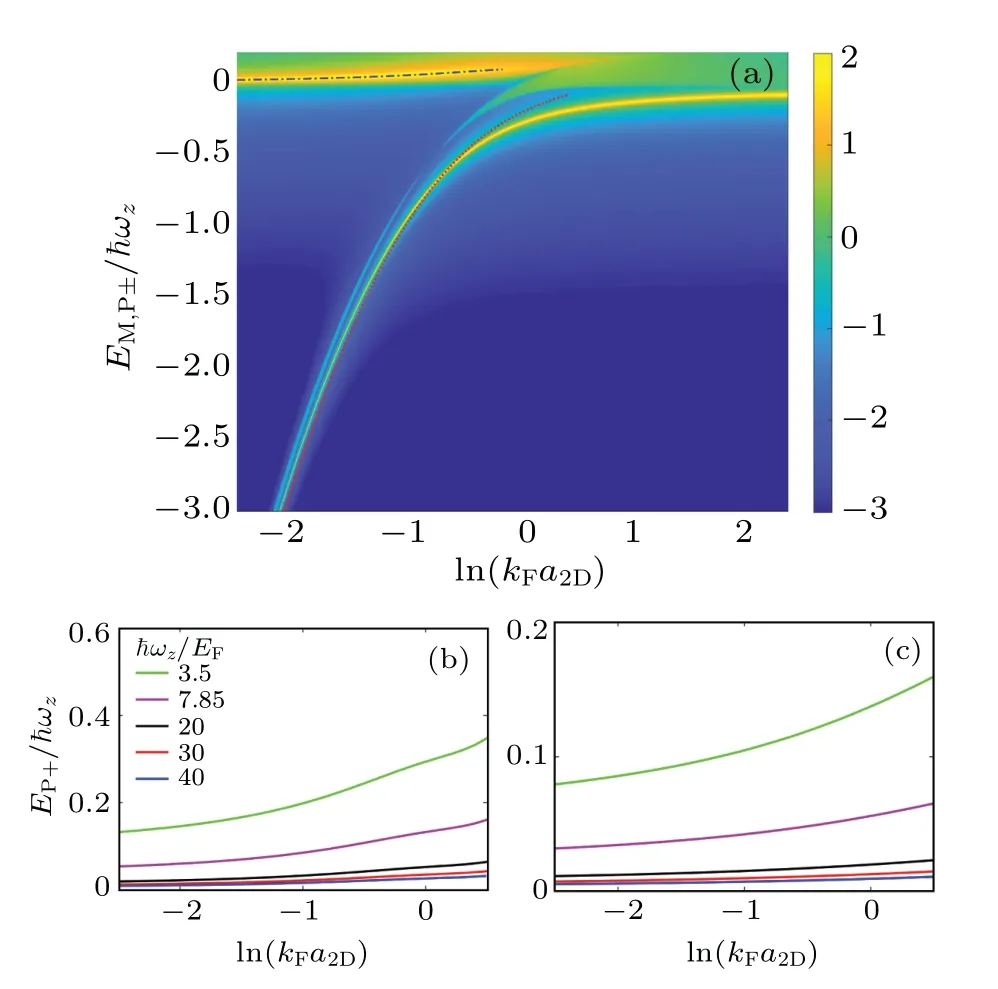
Fig.5. (a)Contour plot of the spectral function Log10A(Q=0,EP)of the polaron state for a gas of 40K with ¯hωz/EF =7.85. The red dotted line is the molecule energy obtained from Eq. (8). On the BCS side,the repulsive polaron branch(blue dotted-dashed line)merges into the molecule–hole continuum which is denoted by the broad light area. (b),(c)Repulsive polaron energy EP+ with(b)η=1 and(c)η=6.64. The five lines from bottom to top represent ¯hωz/EF =40,30,20,7.85 and 3.5,respectively. The color code is similar to Fig.4.

4. Conclusion

We study the impurity problem in a background of fermionic particles trapped in a quasi-two-dimensional confinement. Using an effective two-channel model which incorporates the effect of excited states along the strongly confined direction,we investigate various properties of the polaron and molecule states,including the eigenenergy,wave function,effective mass, and the spectral function. Since the transversal trapping potential for a quasi-two-dimensional configuration is finite,the system acquires another energy scale of ¯hωz,and hence breaks the universality which is present in a strictly two-dimensional Fermi gas with contact interaction. Specifically,we find that the polaron–molecule transition point shows a strong density dependence on ¯hωz/EFfor all mass ratios.This observation is of particular interest when analyzing experimental results of cold atomic gases trapped in harmonic potentials,where the density is non-uniform.

Acknowledgements

We thank support from the National Key R&D Program of China (Grant No. 2018YFA0306501), the National Natural Science Foundation of China (Grant Nos. 11522436,11774425, and 12074428), and the Beijing Natural Science Foundation(Grant No.Z180013).