Pulsed high-current discharge in water:adiabatic model of expanding plasma channel and acoustic wave
2022-04-15KOZYREVZHERLITSYNandSEMENIUK
A KOZYREV, A ZHERLITSYN and N SEMENIUK
Institute of High-Current Electronics, Russian Academy of Sciences, Tomsk 634055, Russia
Abstract This paper presents the results of a theoretical and experimental study of the use of a pulsed discharge in water to obtain a strong acoustic wave in a liquid medium.A discharge with a current amplitude of 10 kA,a duration of 400 ns,and an amplitude pulsed power of 280 MW in water at atmospheric pressure created an expanding acoustic wave with an amplitude of more than 100 MPa.To describe the formation of the discharge channel,an isothermal plasma model has been developed,which made it possible to calculate both the expansion dynamics of a highcurrent channel and the strong acoustic wave generated by it.Our calculations show that the number density of plasma in the channel reaches 1020 cm–3, while the degree of water vapor ionization is about 10%, and the channel wall extends with a velocity of 500 m s-1.The calculations for the acoustic wave are in good agreement with measurements.
Keywords: plasma applications, electrical discharge in water, dense plasma channel
1.Introduction
Pulsed high-current discharges in liquids and their associated shock waves have a high potential for practical application.Investigations of shock waves in water are carried out to achieve mineral liberation [1, 2], refinement of hydrothermal quartz [3], destruction of concrete and reinforced concrete structures[4,5],recycling of fibrous composite materials[6],electronic scrap [7, 8], and photovoltaic panels [9, 10].
One of the main limitations of the extensive use of technologies based on shock waves is the low efficiency of transformation of the electrical energy in the capacitive storage of the supply generator into the mechanical energy of an acoustic wave, which in many cases does not exceed a few percent [11].The acoustic efficiency can be significantly improved by using the electrical explosion of metal wires to initiate a discharge in water.For example, the energy in a wave reaches ~15%of the stored energy[12,13]in the case of using a single wire and up to 24%when using a planar wire assembly [14].A variant of covering electrically exploded wires with energetic materials has been considered [15].However, these methods are not technologically advanced.
Numerous experimental studies are aimed at increasing the intensity of shock waves and revealing their dependence on the electrical parameters of the generator and the discharge, such as the energy in the supplying capacitor bank at the time of breakdown [16], the energy transferred to the discharge channel [17], the length of the discharge channel[18, 19], or the distance from the channel [20, 21].Usually,on the basis of experimental data, a number of empirical dependencies are formulated that are subsequently the subject of theoretical research.For example, the identification of a number of functional dependencies was obtained in numerical calculations based on a 0-dimensional hydrodynamic model.This model used the empirical dependence of the channel resistance Rch(t) on its fixed length l and the energy input from the discharge circuit E(t) was used [22, 23]:
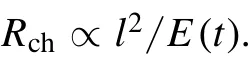
In this work, which does not use any empirical dependencies,a mathematical model of the development of a plasma channel in a liquid medium is formulated in relation to the technical parameters of the experiment.The model is based on the hypothesis of an isothermal state of the plasma in the channel of a pulsed high-current discharge.A calculation of the dynamics of an acoustic wave is made on the basis of a theoretical description of the plasma channel.The divergence and reflection of the wave in the experimental design of the discharge chamber is taken into account.The model of the dynamics of the expanding channel makes it possible to calculate the intensity of the acoustic wave under specific experimental conditions.
2.Expanding channel model
The simplest circuit for generating a high-current discharge can be represented by a series RLC circuit.Discharging of capacitance C previously charged to voltage U0through active resistance R, the inductance of the circuit L, and the plasma channel can be described by the traditional differential equation for the voltage across the capacitor UC:

The variable resistance of the plasma channel Rch(t)is subject to theoretical modeling.The current in the series circuit (current through the channel) is easily defnied asI(t)= -C(dUCdt).The channel voltage can be found by using the ohmic resistance,U(t)=Rch(t)I(t).The electric power introduced into the channel is equal toW(t)=Rch(t)I2(t).
2.1.Plasma channel resistance
In our model, the channel has the shape of a cylinder with a uniform distribution of all parameters along the radius.The assumption that the channel is homogeneous is an approximation of our model.This approximation allows us to use ordinary differential equations instead of partial differential equations.This approximation greatly simplifies the mathematical description of the phenomenon.
The resistance of a plasma channel depends on resistivity ηeand cross-sectional area S.Both of these quantities change over time: the resistivity ηe, due to increasing the number density of electrons ne(t)and gas molecules n(t),in the channel,and the area due to increasing the radius,S(t)=πr2(t).
Moreover, we assume a three-component gaseous medium inside the channel(free electrons, a single type of singly charged ions, and neutral atomic particles) and an isothermal plasma with a fixed temperature T (11 600 K).The plasma pressure was determined by the ideal gas law,P=nkT(where k is the Boltzmann constant).We assume that such an approximate description for a dense gaseous medium inside a thin conducting channel is quite acceptable.The description sufficiently simple to construct a working model of a very complex phenomenon while at the same time allowing control of the main parameters of plasma processes.
The resistance of a plasma channel of length l and crosssectional area S for a wide range of concentration of free electrons can be determined by the expression [24],
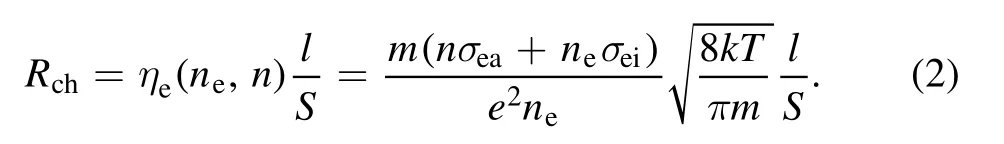
Here m and e are the electron mass and elementary charge,σeaand σeiare the transport cross sections for collisions of electrons with neutral atomic particles and with positive ions,respectively, andηe(ne,n)is the plasma resistivity.
Equation (2) describes the resistance of both weakly ionized and strongly ionized plasmas, for which the dependence on the concentration of free electrons is nonlinear.For simplicity, we assumed the cross sections of elementary processes to be known and constant (σea=10-15cm2and σei=10-13cm2), but the dependence of the transport cross section of Coulomb collisions σeion the average electron energy is not difficult to take into account retroactively.
2.2.Dynamics of the electronic component
The 0-dimensional kinetic equation was used to describe the dynamics of the electron number density.According to the equation,the rate of electron generation is proportional to the power density W(t) introduced into the gas, and the rate of loss is determined by the free diffusion of electrons onto the walls of the cylindrical channel [24]:
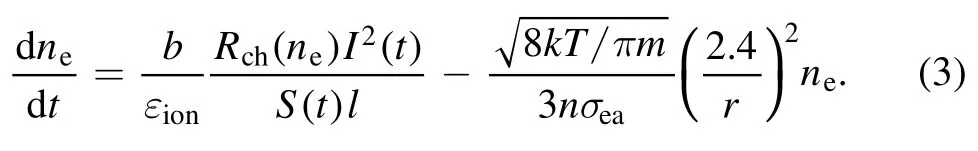
Here εionis the ionization energy of an atom or molecule of a gaseous medium.The dimensionless coefficient b characterizes the relative share of the energy deposited in the gaseous medium, which goes into ionization processes.For example,b=0.04 for a discharge in molecular nitrogen[25].In fact, both of these parameters can be combined by determining the ‘energy cost of ionization’,εionb.This energy cost reflects the average electrical energy required to generate one free electron in the plasma.In the theoretical model, the‘ionization cost’ (along with the plasma temperature T) is an adjustable parameter and is found by comparing the calculation with experimental data.
2.3.Dynamics of the entry of matter into the channel
The pressure of the neutral gas in the channel, described by the ideal gas lawP=nkT,increases due to the evaporation of the condensed phase of the substance from the channel walls.According to the well-known model [26], the evaporation of water molecules occurs as a result of intense surface heating by thermal radiation of the channel wall,which is in the condensed phase.The growth of the gas number density n is described by the balance equation for neutral gas particles in the channel:

Here σSBis the Stefan–Boltzmann constant and Devis the average evaporation energy of one water molecule (we use Dev=0.42 eV in our calculations).Temperature T is a key parameter that determines the rate of expansion of the channel and the flow of matter into the gas phase.The strong dependence of the right-hand side of equation (4) on temperature makes it possible to reliably estimate it by comparing the theoretical prediction with experimental data.The characteristic energy input into the channel was at the level of 100 J, the channel diameter was at the level of 1 mm and the length was 20 mm.This volume of liquid water contains about 5×1020H2O molecules.Then the energy input per molecule will be approximately 1.2 eV.Therefore, we believe that it will not be possible to heat the substance to higher temperatures, and lower temperatures are also unlikely, since within the framework of the model, the electron conductivity of the channel cannot be very low.
2.4.Channel expansion dynamics
The linear energy balance equation for the expanding channel(in which the substance has the adiabatic exponent γ) due to the power released in it W(t) has the form,
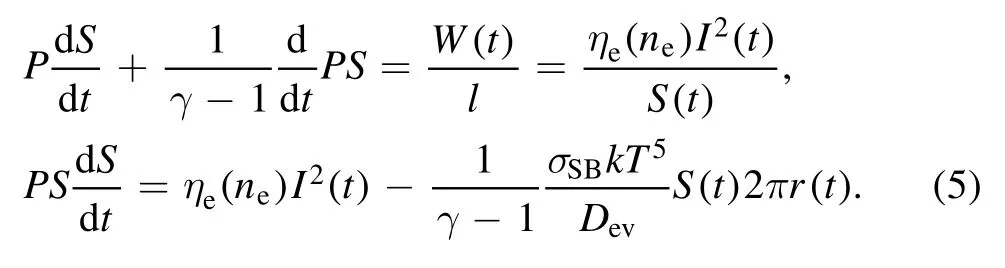
The top equation (5) describes the expansion of the hot channel.The input power W(t) is spent on the work of expanding the channel (the first term on the left side) and an increase in its internal energy (the second term on the left side).Even rough estimates show that the power of energy losses due to radiation and thermal conductivity in the hot channel can be neglected (they are more than 4 orders of magnitude lower than the power input W).The bottom equation(5)is obtained after substituting equation(4)into the first equation.
We now have four ordinary differential equations (1),(3)–(5) for the four functions I(t), ne(t), n(t) and S(t),respectively.To obtain unambiguous solutions to this system,the initial conditions for these quantities were used.Moreover, the initial current in the channel I0was related to other initial parameters by the equation
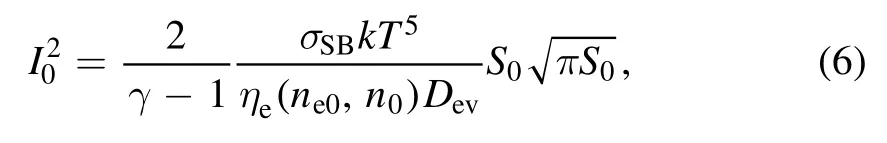
which ensured the physical agreement of the initial conditions.
3.Experimental setup
The model has been tested in relation to experiments carried out on a generator with a sub-microsecond discharge time.The schematic of the experiment is shown in figure 1.The discharge chamber uses a configuration with a sharply inhomogeneous electric field.The discharge occurs between a flat potential electrode and a grounded electrode made in the form of a thin-walled cylinder 25 mm in diameter.
The volume of the crushing chamber was filled with water with a specific electrical resistance of ~105Ω·cm.The equivalent parameters of the RLC discharge circuit of the generator were as follows: C=8 nF, L=2120 nH, and R=1.5 Ω.A charging voltage of U0=210 kV results in 176 J of energy in capacitive storage.
In the experiments,the voltage U1at the generator output was recorded using a capacitive voltage divider,the discharge current I using a Rogowski coil, and the derivative of the discharge current dI/dt using a B-dot sensor.The location of the sensors is shown in the figure 1.
These parameters allow us to calculate the power and energy released in the discharge channel.Using the known generator capacitance C=8 nF and the current waveform when the gap in the chamber was short-circuited, the equivalent resistance of the generator circuit R=1.5 Ω and its total inductance L=2120 nH were determined.The inductance L2between the voltage sensor and the high-voltage electrode of the chamber was also determined, which is used to calculate the voltage, U, on the discharge channel:U=U1-L2(dI/dt).
In addition, a hydraulic pressure pulse was measured using a PS-02 sensor (Globaltest, Russia) with a diameter of 8 mm.The location of the sensor is shown in the figure 1.
Examples of typical waveforms are shown in figure 2.Energy of ~70 J with a peak power of ~300 MW is injected into the channel.A pressure pulse with amplitude of~15 MPa and FWHM duration of ~6 μs is recorded at the location of the sensor.
4.Calculation of the parameters of the expanding channel and model calibration
The channel dynamics were described by a system of four equations (1), (3)–(5), with the initial parameters: r(0)=0.1 mm, l=20 mm, ne(0)=1010cm-3, P(0)=105Pa, T=11 600 K (this temperature is equivalent to an energy of kT=1 eV),and γ=1.26.The initial current in the channel is I(0)=3.5 A (according to expression (6)).The parameters of the discharge circuit were taken the same as in the experiment:C=8 nF, L=2120 nH, R=1.5 Ω, and U0=210 kV.
The duration and energy of the calculated power pulse can be fit to the experimental profile by substituting the‘ionization cost’of 360 eV into equation(3),which is a quite reasonable parameter.
After such a calibration of the theoretical model, it is possible to identically calculate all the main parameters of the plasma channel.Figure 3(a) shows the calculated and experimental profiles of the inserted discharge power.Figure 3(b)shows the time dependences of the channel radius and the number density of free electrons in the plasma.

Figure 1.Scheme of the experiment with a discharge in water: 1—high-voltage electrode, 2—grounded electrode, 3—discharge channel, 4—pressure sensor.
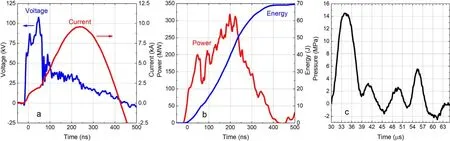
Figure 2.Waveforms of the discharge voltage and current(a),their conversion into power and input energy(b),and the profile of the pressure pulse of the acoustic sensor (c).

Figure 3.Calculated profiles of power (a), electron number density in the channel (b, dashed lines), and channel radius (b, solid lines) for 400 ns (red lines) and microsecond (blue lines) generator discharge times.

Figure 4.Instantaneous pressure distributions in the acoustic wave at different times after the start of the discharge (the scale on the right shows the compression-rarefaction pressure in MPa).
To determine the effect of the generator discharge time,the channel parameters were calculated at a close level of energy stored in the capacitor, but at microsecond discharge duration.The circuit parameters in the calculation of the‘long pulse’ were C=30 nF, U0=100 kV, L=3300 nH, and R=0.93 Ω, and the other parameters were the same as for the ‘short pulse’.The calculated power pulse is shown in figure 3(a)by the dashed line,and the corresponding channel parameters are shown in figure 3(b).
According to our calculations, the electron number density in the channel stops increasing by the end of the power pulse.Despite the twofold change in the amplitude power of the energy input in the short and long pulse modes and the corresponding almost twofold difference in plasma concentrations,the channel radius increases at approximately the same rate.
Several comments should be added about the state of the plasma in the discharge channel.By the end of the power pulse, the channel radius reaches 0.6 mm, and the channel length is 20 mm.The density of the deposited energy is thenQ~70 J 2.26 ×10-8m3≈ 3 ×109J m-3.Energy deposited on one gas particle is described byε1≈Dev+kT/(γ- 1)≈4.5 eV.The number density of molecules in the medium can then be estimated asn≈Q/1ε≈4 ×1021cm-3,which is an order of magnitude higher than the calculated number density of charged particles at the same moment.Even taking into account the roughness of this estimate, we can confidently assume that the plasma in the channel is highly ionized and that equation (2) is quite suitable for this range of number density of molecules and electrons.The plasma in the channel has conductivity close to the Spitzer conductivity, which weakly depends on the electron number density, but quite strongly depends on temperature.This opens up the possibility of additional correction to the calculations,expanding the means of calibrating the model by comparing it with experimental dependences (in this study, we did not use temperature variation).
5.Acoustic wave simulation and comparison with experiment
After calculating the dynamics of the channel radius and power input,these functions were used for the axisymmetric calculation of acoustic waves in the discharge chamber shown in figure 1.In this case, the liquid (pure water,density ρ=103kg m-3, speed of sound cs=1500 m s-1)was assumed to be free of viscosity and thermal conductivity.The equation for an acoustic pressure wave in a homogeneous elastic medium excited by a hot expanding discharge channel on the symmetry axis can be written as follows
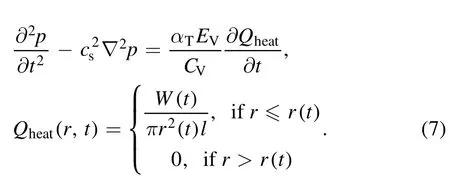
Here, αTis the coefficient of thermal expansion (2.8×10-4K-1),EVis the elastic modulus(2.3×109Pa),CVis the heat capacity per unit volume (4.2×106J·K-1·m-3).For liquid water under normal conditions, the dimensionless coeffciient in equation (7)αTEV/CV=0.15.The 2D evolution of the acoustic wave was calculated using COMSOL Multiphysics 5.2 [27].This program can efficiently solve partial differential equations applied to real geometries of experimental installations.The instantaneous locations of the compression-rarefaction fronts are shown in figure 4.The duration of the energy input into the discharge channel was 400 ns.The circle in the pictures shows the location of the pressure sensor in the experimental chamber, and its diameter is 8 mm.
It can be seen that a thin compression-rarefaction front(compression is shown in red,rarefaction in blue)with a sonic velocity cs≈1500 m s-1expands radially from the discharge channel to the outer wall, simultaneously reflecting from the edges of the electrodes.The acoustic pulse width at halfmaximum corresponds approximately to the duration of the energy input into the channel.Figure 5(a)shows the pressure at various points of the discharge chamber located along the dashed line shown in figure 4.The distance of the observation point from the axis of symmetry is indicated.As can be seen from the calculation, the pressure amplitude reaches Pmax≈160 MPa near the axis of the system, gradually decreasing to several hundred atmospheres at the periphery of the discharge chamber due to the divergence of the front.
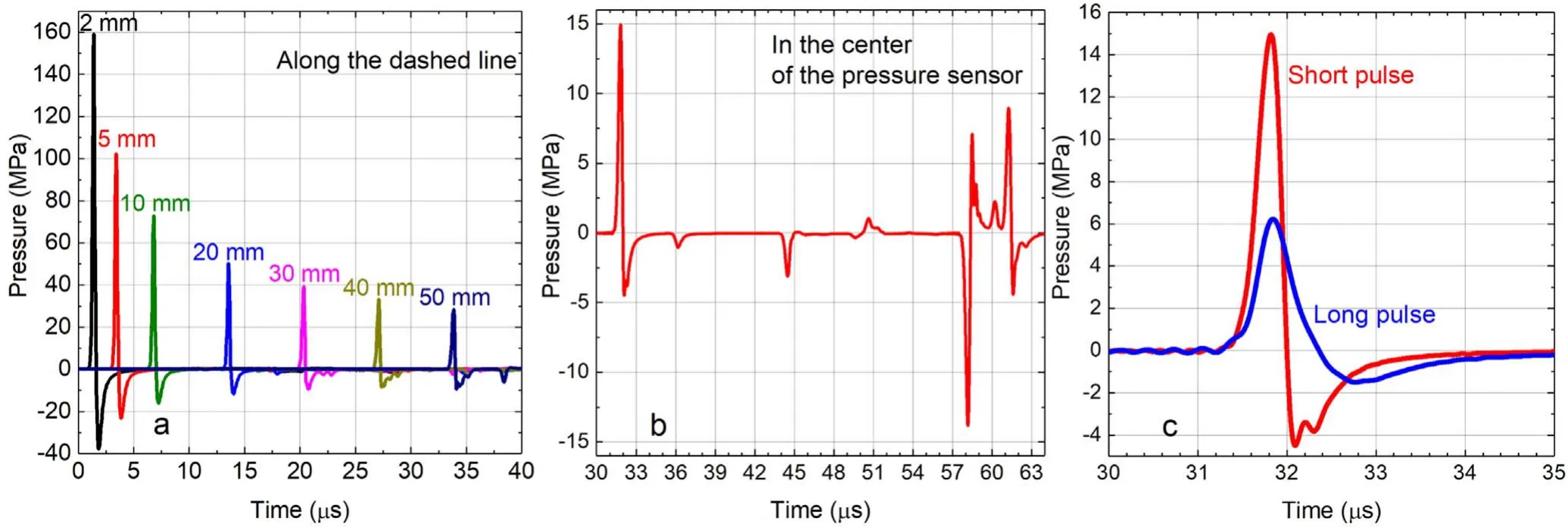
Figure 5.Local time profiles of pressure at different points along the dashed line in figure 4(a),at the point where the center of the pressure sensor is located (b), and a comparison of pressure in discharge modes with duration of 400 ns and 1 μs (c).
It is easy to estimate the total energy of the acoustic wave from the figure 5(a).Thus, at a distance r=5 mm from the axis,the wave front shape is close to cylindrical,the pressure amplitude here is Pmax≈100 MPa, and the peak duration at half maximum Δt≈0.3 μs.Then the peak intensity of the acoustic wave isJmax=Pm2ax2ρcs≈3.3 ×109W m-2,and the integral wave energy can be estimated asEtot=JmaxΔt·2πrl≈0.62 J.
Figure 5(b)shows the time dependence of the pressure at the center point of the dashed circle.At the location of the sensor,the center of which has a vertical coordinate of 32 mm and a radial coordinate of 47 mm, the maximum pressure is 16 MPa.As can be seen, the duration of the calculated acoustic pulse does not exceed 0.5 μs.However, in the experiment, the sensor shows the same amplitude, but the pulse duration is an order of magnitude longer,~5 μs.This is quite understandable, since in the experiment the sensor recorded the long process of the sound wave passing through the aperture D=8 mm,which is on the order of Δt~D/cs.
Figure 4 shows an acoustic wave calculation.These facilitate the interpretation of the local pressure profile in figure 5(b).Large negative pressures in the calculations were obtained because we did not take into account the possibility of liquid rupture and the formation of bubbles.
Figure 5(c)shows a comparative calculation of the acoustic signal at the center point of the sensor position for short and long pulses of the discharge current.With an increase in the duration of the discharge power pulse by a factor of 2.5,there is a proportional decrease in the amplitude of the acoustic wave and an increase in its duration.As a result,the long pulse mode should reduce the total acoustic energy of the wave about three times,and the volume force density in a liquid medium by more than six times compared to the short pulse mode.
6.Conclusions
A model of plasma generation in a high-current channel of an electric discharge in water, adapted for engineering calculations,is presented.It has comparative simplicity for describing experimental observations,although it assumes a strong degree of approximation in comparison with the real situation.In particular, we assumed the presence only of three types of particles(free electrons,positive ions,and neutral molecules of the same type), as well as the spatial homogeneity of the plasma channel along its cross-section and length.Despite these, as well as a number of other reasonable simplifications,the developed channel model in a pulsed discharge in water describes well both electrical and acoustic data obtained in the experiment.
For agreement of the model and experimental waveforms of the electric power in the channel,only one fitting parameter was used, this is ‘energy cost of ionization’.The best agreement was obtained under the condition that energy of 360 eV must be deposited into the plasma to create one electron-ion pair.We did not use the temperature variation in the channel to calibrate the data, assuming it to be 11 600 K, so as not to increase the degree of uncertainty in the initial parameters.This degree of freedom in the theoretical model could be added in subsequent studies.
An experiment in which an electric energy of 70 J is introduced into the channel from an electric pulse generator for 400 ns is described.As a result, it was shown that plasma in a highcurrent channel of a pulsed discharge in water is a strongly ionized state of a gaseous medium (degree of ionization ~10%) with a number density of neutral particles of ~4×1021cm-3.The expansion of the outer front of the hot plasma occurs at a subsonic velocity of about 500 m s-1, generating a strong diverging acoustic wave in liquid water with initial pressure amplitude in the pulse above 160 MPa and a base duration of 0.6 μs.The total energy of the acoustic wave is estimated at 0.62 J.
Acknowledgments
The work was carried out within the framework of the state assignment of the Ministry of Science and Higher Education of the Russian Federation on the topic (No.FWRM-2021-0001) and the grant of the Russian Foundation for Basic Research (RFBR), project No.18-29-24079 mk.
杂志排行
Plasma Science and Technology的其它文章
- Design and preliminary test of a 105/140 GHz dual-frequency MW-level gyrotron
- Competitive effect between roughness and mask pattern on charging phenomena during plasma etching
- Reliability improvement of gas discharge tube by suppressing the formation of shortcircuit pathways
- A novel flexible plasma array for large-area uniform treatment of an irregular surface
- Comparison of double layer in argon helicon plasma and magnetized DC discharge plasma
- Physical design of a new set of high poloidal mode number coils in the EAST tokamak
