有效问题：数学课堂学生深度学习的“支点”

汪祝佑

摘要：课堂有效问题的提出，既是一门科学，也是一门艺术，涉及教学内容、教学对象、教师对教学理念的理解以及对教学实践的感悟等因素，是教师综合素养的集中体现。本文从规划有度的导学问题、提炼精准的核心问题和设置合理的拓展问题三个方面做了思考，给学生提供一个有效的学习“支点”，促进学生对数学的理解，帮助学生深度学习，培养学生的数学核心素养。

关键词：有效问题深度学习小学数学

课堂提问是教学过程中师生围绕问题而展开的言语、思想、情感和知识上的交流活动，会直接影响学生学习的成效。有质量的课堂问题，能诱发学生的学习动机，及时引起学生的回应和思考，使学生积极投入到学习活动中，从而提高课堂教学效果。而有效问题的提出，涉及教学内容、教学对象以及教师对数学知识的理解、对教学理念的理解和对教学实践的感悟等因素，是教师综合素养的集中体现。课堂上，如何提出有效问题，促进学生对数学的理解，帮助学生深度学习，笔者做了如下三点尝试。

一、规划适度的导学问题，引导学生主动学习

问题导学指以导学单或研学单为载体，以问题为线索，学生在问题解决的过程中找到研究方向，达到学习目标，从而培养学生自主学习的能力。导学问题是问题导学的主要呈现形式，因此，导学问题要发挥导学功能。建构主义认为学习是学生知识、能力体系在一定环境中自内而外的“生长”，所以找准学生的“最近发展区”尤为重要。导学问题要尊重学生已有的知识经验和认知能力，关注不同层次学生的需求，体现以学生的学为主体。研学单就好比一幅思维导图，能揭示知识的背景和形成的过程，提高学生解决问题的能力;要有探究性和系统性，有利于唤醒学生的学习动机，便于学生探究学习;要有生长性和结构化，能从问题中发现更多更好的问题，培育学生良好的数学素养。

如“认识公顷”一课，设置这样的研学单。

（1）公顷是一个面积单位，你知道1公顷有多大吗？1公顷是多少平方米呢？把你的研究过程记录下来。

（2）请你算出1公顷分别相当于多少个手拉手方形队伍、教室地面、体育馆、校园、你的卧室。（可使用计算器）

（3）通过预习，你还有什么提醒大家的？你还有什么不明白的地方？

参考资料：我们的校园近似长方形，長约140米，宽约70米;福鼎体育馆占地面积约为500 m2;教室、卧室等地方的面积，自己想办法测量;同学们侧平举两手之间的距离约为1.4米。

学生根据研学单课前自主学习，课堂上“组内展学、研学”，然后“师生共学”，侧重解决学生不会的、有争议的、容易混淆的问题。导学问题的规划和实施就好比带领学生去登一座山，要让他们知道登顶的惬意，还要让他们欣赏一路的风景，更重要的是从中积累活动经验：怎样登山？遇到困难怎么办？要注意什么……教学的最终目标是让学生学会学习。学生思维从低阶逐步走向高阶，学生成长从不成熟逐步走向成熟，这些正是我们课堂所需要的。

二、提炼精准的核心问题，引导学生建构知识

核心问题是指针对具体教学内容提炼出的中心问题或主要问题，相对于其他而言最能扣紧教学目标、最有利于学生思考、最能体现知识本质及最具有高阶思维价值的问题。合适的核心问题，聚焦于具体教学内容的重点和难点，有着“画龙点睛”的作用，牵一发而动全身，推动着课堂教学的进程。在教学过程中，教师要对教学内容进行深度解读，基于学生设计精准的核心问题，吸引学生参与问题的思考，帮助学生理解知识，闻一知十，形成知识体系。在课堂上，核心问题通常以“大问题”的形式出现，具有针对性、思考性和开放性，既能直切学生的学习起点和知识的“内核”，关注不同层面学生的思考和学生的差异发展;又能为学生自主思考、积极探索留下空间。

如教学“认识平行四边形”，上课时，学生举例生活中的平行四边形例子并抽象出图形后，利用学具创造平行四边形或在方格纸上画平行四边形。教师可提炼出这样的问题引发学生思考：（1）在创造或画平行四边形的过程中，你觉得平行四边形有哪些特点？（2）小组成员分别说说是怎样发现平行四边形的特点的。有一定张力的核心问题能激活学生广阔的思维空间，通过动手操作、合作交流、尝试说理，学生知其然并知其所以然，平行四边形的认识过程逐步明朗和不断深化。学生掌握平行四边形的特征后，教师趁热打铁引导学生反思认识平行四边形的过程：动手操作——猜想验证——得出结论。核心问题的提炼与加工，直指本课知识的本质，对于学生来说，不仅是理解知识和掌握技能，更是指向思想方法的感悟和活动经验的积累。在后续认识其他平面图形和立体图形时，由于学生已经有了认识图形的经验，相信学生可以得心应手地解决问题。这样，学生在思考互动、合作探究中由“点”到“线”，由“线”到“面”打通知识的内在联系，学生的思维得到自然生长。核心问题就像是一只由内而外打破的鸡蛋，是有生命力的，能催发学生问题意识，带动学生数学思考，指向学生思维深处，从某种意义上说，提出一个核心问题比一千个答案来得更有价值。

三、设置合理的拓展问题，促进学生深度学习

数学课堂教学是为了进一步拓展学生的知识和提高学生解决问题的能力。课堂上，一个合理的延伸性、拓展性问题的提出，不仅能调动学生学习的积极性，还能激发优生的求知欲望，为待优生提供跳一跳也能摘得到“果实”的机会，从而引发学生深层次的思考，灵活地运用知识，多角度思考数学问题，逐步帮助学生形成发散、创新、有深度的思维方式，真正实现深度学习的有效发生。

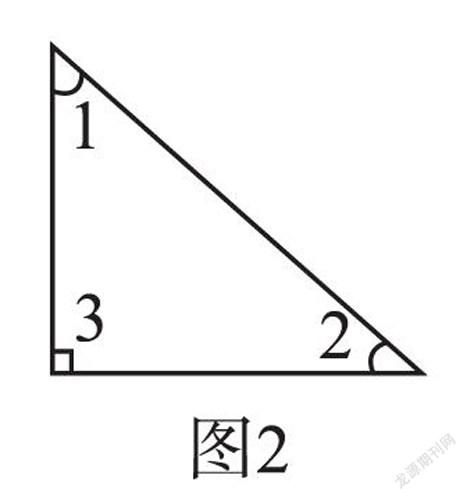
如教学“圆柱的体积”一课时，学生推导出圆柱的体积公式后，教师引导：把圆柱转化成近似的长方体（如图1），我们知道它们之间体积不变，那么什么变了？从而引导学生发现：圆柱转化成长方体后，表面积变大了，而且长方体左右两个面的面积就是半圆柱中的一个长方形（或正方形）面的面积。又如教学“三角形的内角和”一课时，学生动手操作、合作交流并推理验证得出结论——三角形的内角和是180°后，出示图2，思考：一个直角三角形，如果剪去∠2，这时图形的内角和是多少度？一石激起千层浪，学生纷纷表达自己的看法，有的同学还是坚持自己的观点，认为是180°，如图3的两种情况;有的同学说不是180°，剪去情况如图4。出示图4后，教师追问：剪去∠2后，这时变成了什么图形？内角和是多少度？如果是五边形或六边形呢……启发学生猜想，留下悬念，有着“课虽尽而意无穷”的效果。这样，合理、灵活的拓展，要么是对教材空白的填补，要么是对知识内容的延伸，真正做到不是教教材，而是用教材教。

问题是教师课堂教学不可回避的话题，站在学习者的视角设计问题，才能真正回答“学生需要学什么”“学生要怎样才能学会”“学生学会后有哪些成长”等问题，也只有回答了这些基本问题才能称得上是有效提问。因此，课堂教学的有效问题要力求将学习目标、学习内容、学习动机、适时互动和自然生长“无缝”衔接，给学生一个有效的学习“支点”，帮助学生深度学习。

责任编辑：赵潇晗