基于勒让德多项式逼近的钻孔岩性分布特征预测模型

2022-04-14王权铭杨宇江路增祥

金属矿山 2022年3期

王权铭杨宇江，2 路增祥，2 马驰曹朋

(1.辽宁科技大学矿业工程学院，辽宁鞍山 114051;2.辽宁省金属矿产资源绿色开采工程研究中心，辽宁鞍山 114051;3.北京科技大学土木与资源工程学院，北京 100083)

穿孔作业是露天矿山开采中高耗能、高耗时的生产工序[1-6]，缩短穿孔作业时间是提高矿山生产效率、降低生产成本的有效措施之一。矿岩的物理力学特性及其分布特征对于确定穿孔位置、间排距等炮孔设计参数，选择钻机钻头，调整钻速和钻压等影响重大[7-9]，且直接影响着钻机的穿孔速度，进而影响了矿山的开采效率[10-12]。准确预测采场岩性及其分布特征能够为矿山穿孔爆破设计工作提供基础资料，也能帮助钻机操作人员预判穿孔位置矿岩的可钻性，更好地操控钻机作业[13-15]，以缩减穿孔时间，提高矿山开采效率。

为研究精确可靠的岩性预测方法，刘向君等[16]提出了以神经网络技术为基础的岩石强度预测方法;王棣等[17]采用神经网络BP算法建立了能够估计二维地震剖面的地层岩性预测方法;曹正林等[18]认为钻井参数与岩性有直接或间接的关系，据此可在钻进过程中随时了解地下岩层情况。张建林等[19]根据波阻抗与岩性之间具有一定的概率相关关系，综合应用多学科信息，建立了预测岩性圈闭随机模拟方法。刘向君等[20]针对在室内常温常压下进行岩石微可钻性试验存在的可钻性数据离散、随机、有限、成本高等问题，采用物理模型方法推导出利用了声波测井资料预测岩石可钻性的计算模型，并结合S油田实际资料开展了钻速预测方法研究。此外，支持向量机[21]、灰色理论[22]也被应用于岩性预测工作中。上述研究大多采用机器学习方法对岩性进行预测，虽然该类方法可以从变动的样本数据中进行动态学习，但所需钻孔数据量较大，有时需要人为建立某种模型对其进行指数倍的筛选，使得该类方法应用存在一定的局限性。

上述研究在促进岩性预测发展方面具有重要价值，但大多是围绕石油勘探钻井问题展开，针对金属矿山露天采场岩性预测的研究涉及较少。本研究以最佳函数逼近法为基础，采用勒让德多项式建立金属矿山露天采场的岩性预测模型，利用有限的钻孔岩性分布特征信息，预测待穿孔位置的矿岩分布特征，为矿山穿爆设计和穿孔施工提供依据。

1 基本原理

1.1 函数逼近法

函数逼近法是一种应用较广泛的函数拟合方法[23]。使用该方法建立预测模型时既不需要大量的数据进行推导，也不需要根据特定模型进行处理，具有简单、灵活等特点。

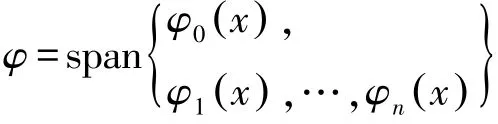
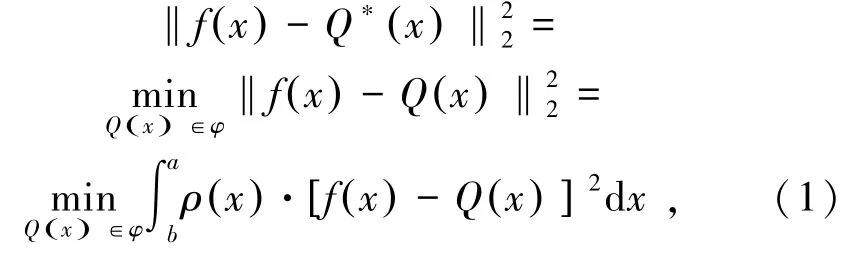
式中，C[a，b]表示在[a，b]上连续的全体函数组成的集合;span{·}为向量张成的线性空间;Q*(x)为f(x)在子集φ∈C[a，b]中的最佳平方逼近多项式;ρ(x)为权函数。

式(1)等价于求多元函数I(a0，a1，…，am)的最小值，其最小值为

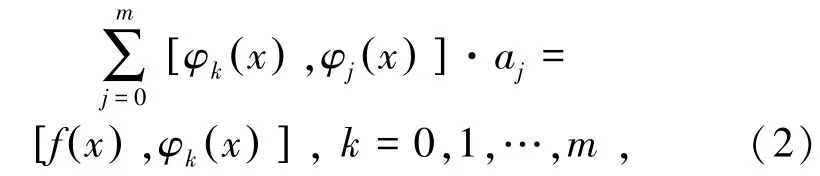
式中，aj为回归系数;I(a0，a1，…，am)为关于a0，a1，…，am的二次函数;m表示m元函数。

式(2)是关于aj(j=0，1，…，m)的线性方程组。设φ0(x)，φ1(x)，…，φm(x)是权函数ρ(x)的正交函数族，得到

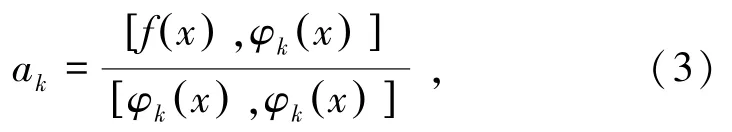
式中，ak代表第k个线性方程组的回归系数;[f(x)，φk(x)]表示首项系数为1的最大公约式。

1.2 勒让德多项式

勒让德多项式是权函数ρ(x)≡1在区间[-1，1]上由{1，x，…，xn}正交化得到的多项式[24]:

式中，n为阶数。

作为一种正交多项式，勒让德多项式具有系数之间相互独立的特点，其正交对数矩阵具有较小的偶然性且只会影响其中的某一项，使用勒让德多项式预测可以极大地减少误差。因此该方法被广泛用于预测模型构建、误差分析、参数选择等方面[25]。

2 岩性分布特征预测模型

露天矿穿孔作业过程中，会遇到具有不同力学特征的矿岩体。根据矿岩特性的不同，适时调整钻机的钻速及钻压，有利于提高穿孔速度。根据先期地质钻孔所揭露的地层特征信息，建立待穿孔位置的矿岩层岩性预测模型，对于预判矿岩分布特征具有重要的工程意义。

将已知的钻孔地层特征作为样本信息，以最佳函数逼近法为基础，采用勒让德多项式建立穿孔位置的岩性预测模型，流程如图1所示。

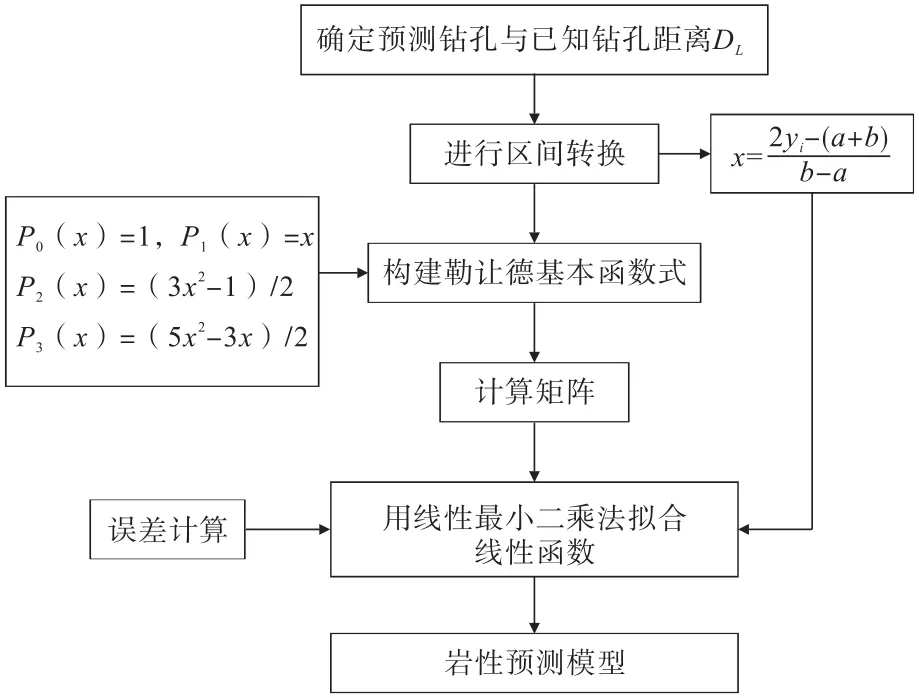
图1 基于勒让德多项式的岩性预测建模流程Fig.1 Thology prediction modeling process based on Legendre polynomial

对已知钻孔穿过的各岩层依次记为yi，则区间变换表达式为

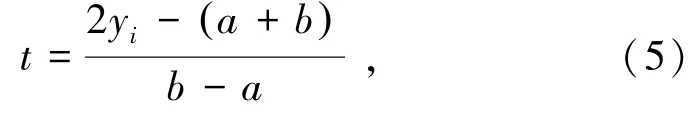
式中，t为勒让德变量;yi为钻孔的层段编号，i=1，2，…，n;a为岩层最顶端标高;b为某岩层的底面标高。

此时，t取值处于[-1，1]区间，相应的概率密度为f(yi)，其均值M0和原点矩MK可进行如下计算:

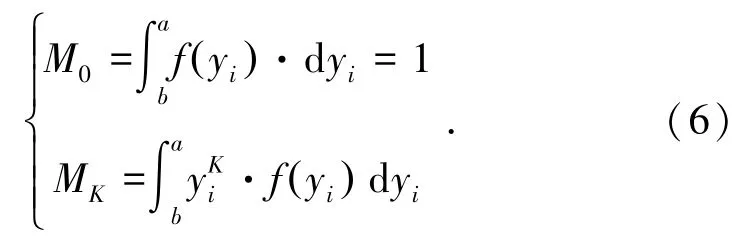
根据辛钦大数定律[24]，原点矩和K阶原点矩相等，即

式中，AK表示K阶原点矩。

由于勒让德多项式具有正交性和奇偶性，由其递推公式可得到:

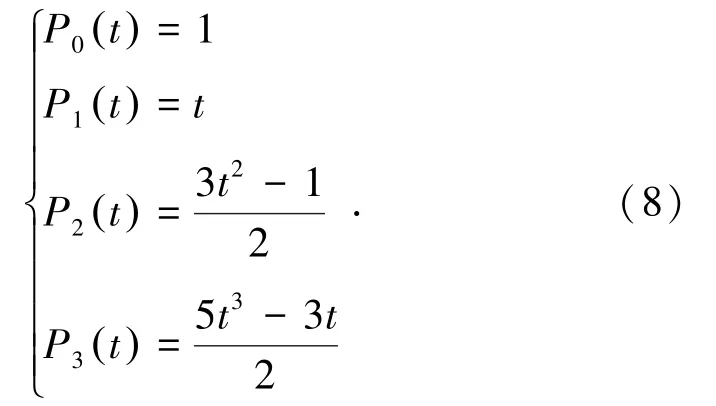
以勒让德多项式进行几何参数化建模，用λ表示第i个钻孔基于勒让德多项式的误差值进行建模。对勒让德多项式以λ为基函数进行展开，得到:

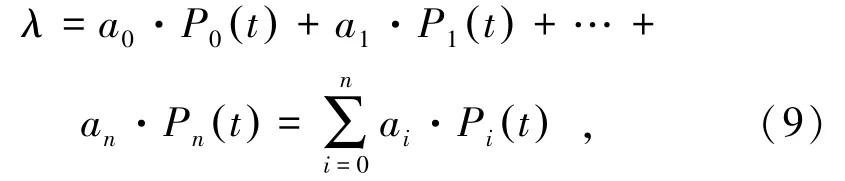
式中，a0、a1、…、an为回归系数。

用最小二乘法展开式(9)得到:

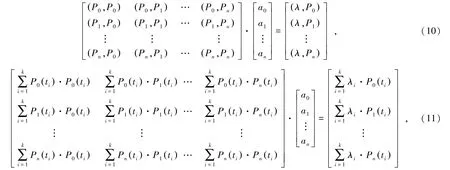
式中，k为钻孔穿越岩层的总层位数;i表示第i个钻孔;λi为第i个钻孔基于勒让德多项式的误差值;ti表示第i个钻孔勒让德变量值;Pn(ti)表示n阶勒让德多项式值。

由式(4)与式(9)可得到如下预测模型:

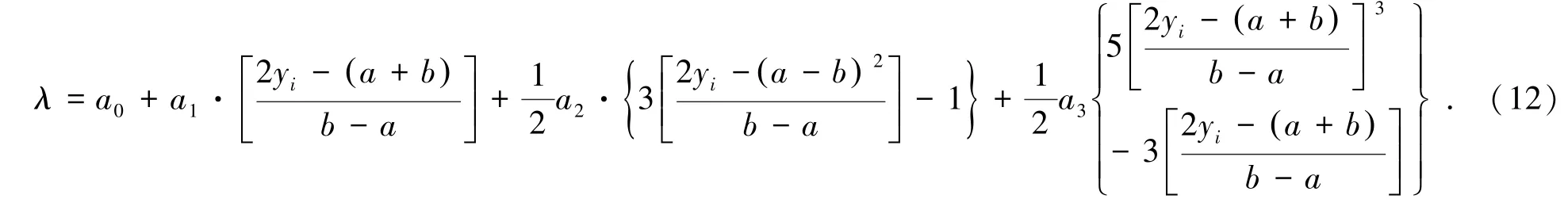
简化式(12)，可得到:

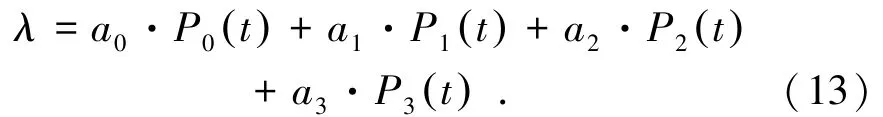
则预测误差值δ可进行如下计算:

式中，DL为预测钻孔与某一个已知钻孔间的直线距离。

3 预测模型可靠性验证

3.1 基础钻孔资料

根据某铅锌矿床的ZK2201和ZK4201钻孔数据，验证预测模型的可靠性。两钻孔所揭露的岩层分布特征见表 1。ZK2201、ZK4201钻孔和预测钻孔ZK3201的位置关系如图2所示。

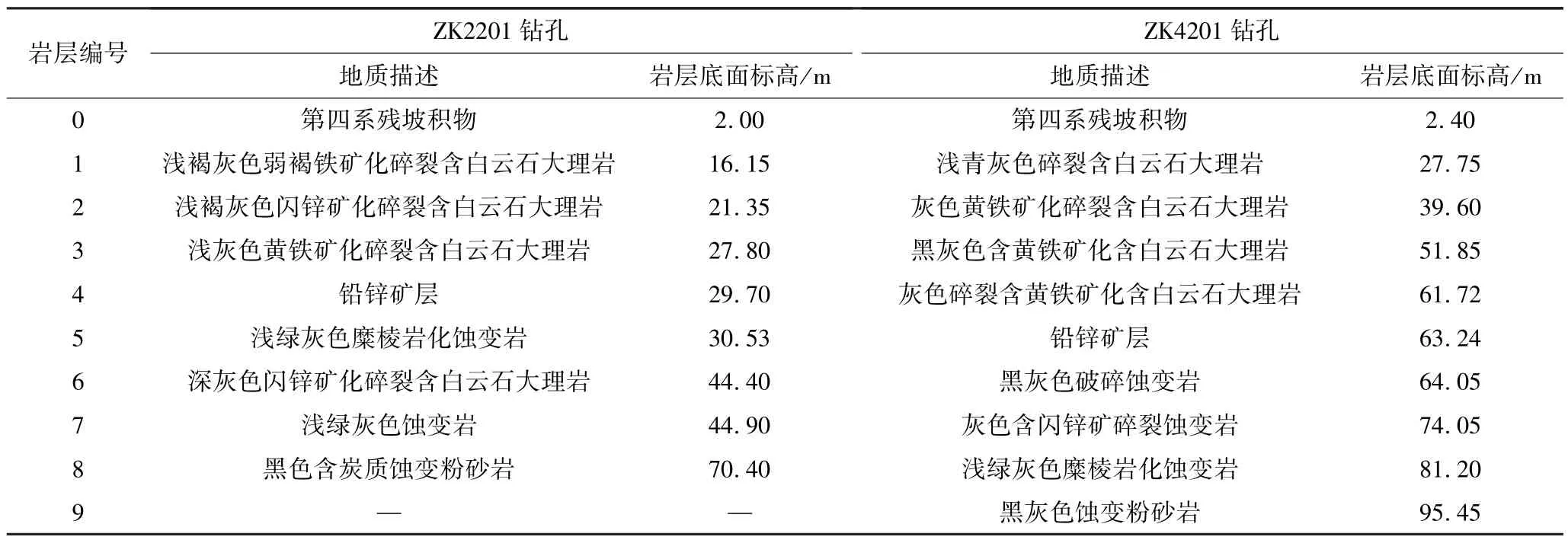
表1 ZK 2201、ZK 4201钻孔位置的岩层信息Table 1 Rock stratum information of ZK 2201 and ZK 4201 drilling hole

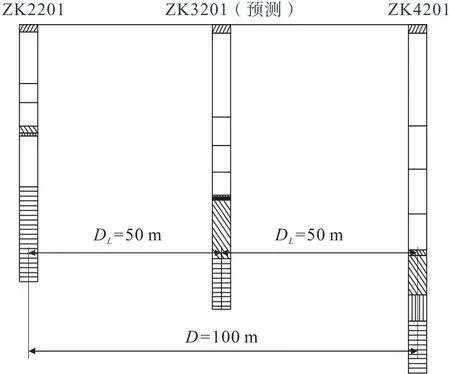
图2 预测钻孔与基础钻孔岩性及厚度对比Fig.2 Comparison of lithology and thickness between predicted borehole and base boreholes

3.2 待穿孔位置岩层特征信息预测

以待穿孔钻孔位于ZK2201和ZK4201钻孔正中间为例(该处实际存在ZK3201钻孔，为验证预测结果的可靠性，假定其岩层信息未知)，根据表1给出的已知钻孔岩层特征信息，采用建立的模型预测待钻钻孔的岩层信息。

根据表1中各岩层的厚度，采用式(11)、式(12)、式(14)计算，可得到待穿孔处对应的岩层厚度误差及对应的勒让德多项式函数值见表2。

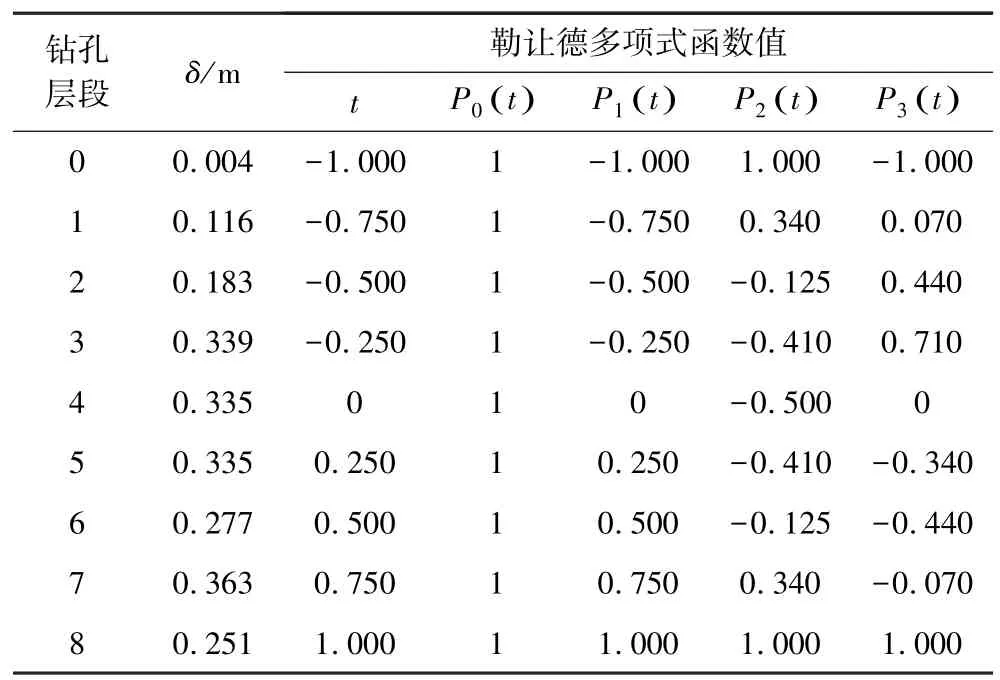
表2 待穿孔处对应误差及勒让德多项式函数值Table 2 Corresponding errors and Legendre polynomials function values at the hole to be drilled

对表2，根据式(11)取k=9，n=3(勒让德阶数)，建立矩阵关系式:

对式(15)求解，得到对应的回归系数为a0=0.259 7，a1=0.118 4，a2=-0.131 4，a3=0.028 4。

根据计算式(13)得到的回归系数，由预测模型建立待穿孔处的勒让德基函数的误差拟合多项式模型:

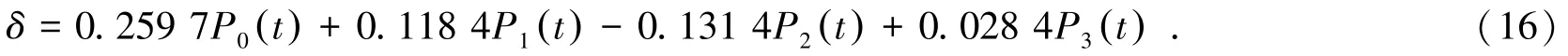
根据式(8)和表2，由式(16)可得到:

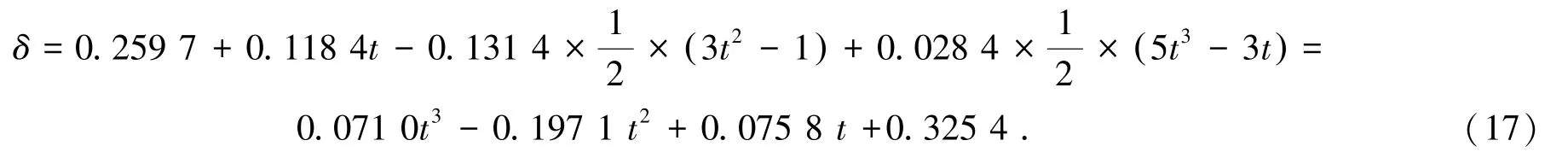
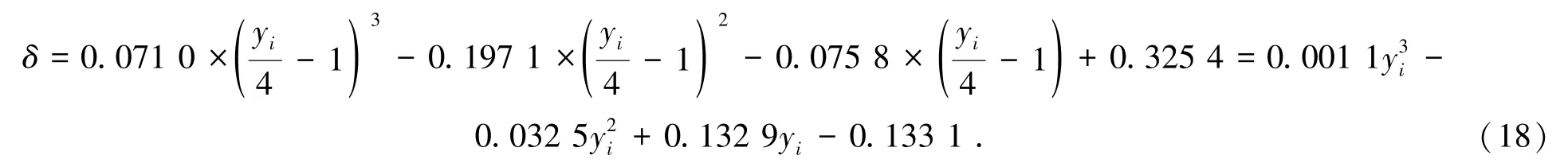
根据表1，取层段最小值为待预测层段数量，为9 个层段，即i=0，1，2，…，8。对式(18)赋予不同的值，每隔1层段将2次钻孔数据进行一次比较，可计算出待穿孔位置处不同岩层的厚度。结合ZK2201钻孔和ZK4201钻孔岩性柱状图，根据表1及待穿孔处岩性预测结果，得到预测钻孔与基础钻孔的岩性及其厚度对比如图2所示。

3.3 预测结果

将待穿孔位置的岩性特征预测结果与该位置的实际钻孔(ZK3201)岩性特征信息进行了对比，结果见表3。

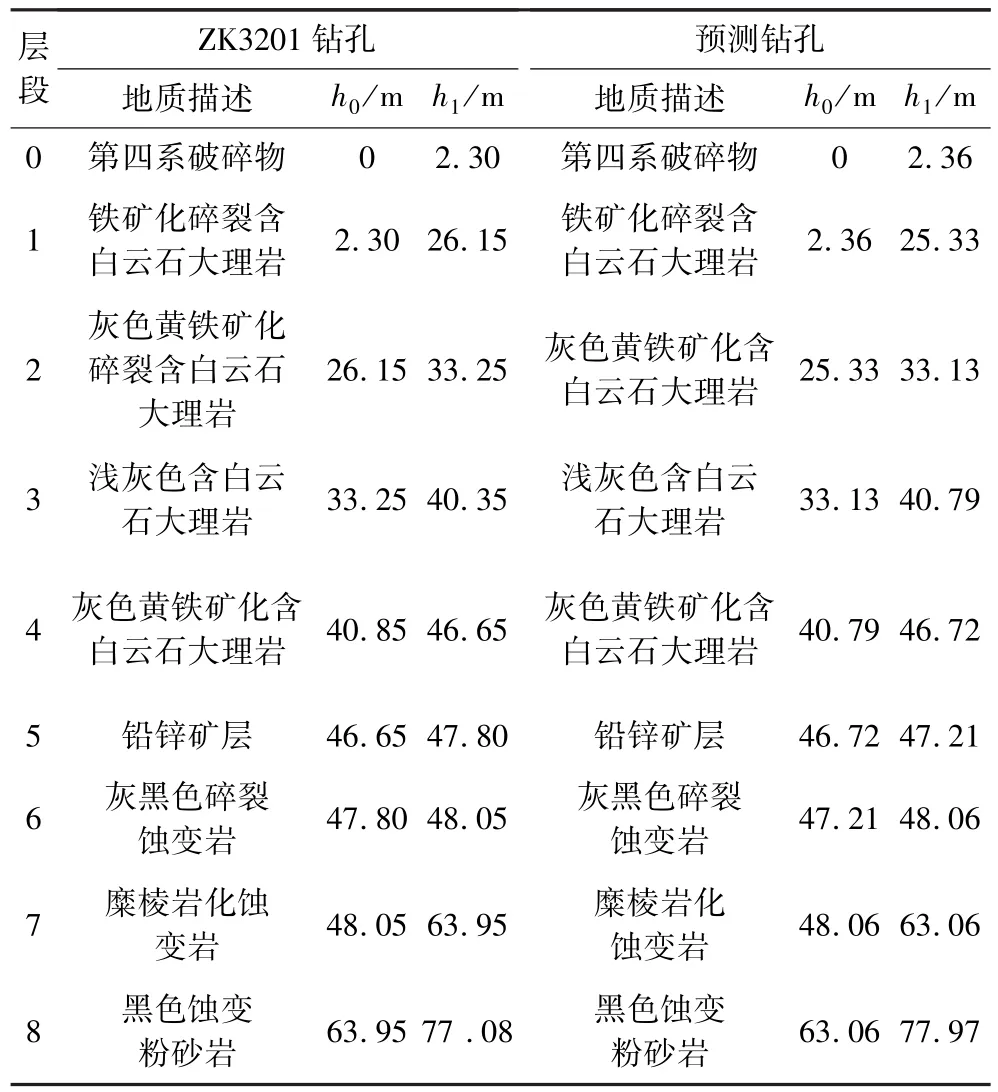
表3 待穿孔位置岩性特征预测结果与实际ZK 3201钻孔信息对比Table 3 Comparison of lithological feature prediction results of the position to be drilled with information of actual ZK 3201 drilling hole

由表3可知:预测的岩性厚度与标高分布与该处的实际钻孔信息基本相同，预测结果与实际信息误差相对较小，如图3所示。

预测误差大小与基础钻孔的数量、间距以及预测钻孔与某一个已知钻孔间的直线距离大小相关。由图3可知:在本研究给定条件下，由于自然界岩体在空间展布上的不均匀性和复杂性，基础钻孔数量仅有2个且相距较远，采用勒让德多项式建立的钻孔岩性预测模型对待预测位置处的钻孔岩性进行预测，最大误差为3.12%，总体误差相对较小。在矿山实际穿孔作业中，当炮孔距离较小(一般为2.5～4.5 m)，且可利用的钻孔信息较多时，本研究方法的预测误差会进一步减小。采用本研究方法进行钻孔岩性分布预测，在一定程度上可以满足矿山穿孔作业需要。