高阶段嗣后分层胶结充填体强度及结构优化研究

熊朝辉 谭玉叶 楚立申 宋卫东

(1.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083;2.北京科技大学土木与资源工程学院，北京 100083;3.武钢资源集团大冶铁矿有限公司，湖北 黄石 435006)

高阶段空场嗣后充填采矿法具有开采效率高、可有效管控地压、矿石回收率高、损失贫化水平低等特点，在地下金属矿山得到了广泛应用[1-3]。一步骤高阶段嗣后充填体受荷破坏主要在底部及顶部位置[4]，中间部位受力较小，在失稳破坏后，中间部分充填体保持稳定状态。考虑到胶结充填成本占到采矿成本25%～30%[5-6]，通过优化充填体中间层强度及结构，降低充填成本，对于提高矿山经济效益具有重要意义。

针对阶段空场嗣后充填法中单侧揭露充填体强度要求的问题，国内外学者主要采用经验类比法、数值模拟分析法、力学模型法等进行研究。加拿大MITCHELL等[7]考虑胶结充填体与侧壁围岩黏结作用，提出了一种基于极限平衡法的解析计算模型;LI等[8-9]在经典解析方法的基础上，考虑充填成拱作用及围岩与充填体之间的摩擦作用，进一步修正发展了Mitchell法;张常光等[10]在此基础上考虑采充时序，得到了更加合理的强度值。然而，以上解析模型均未考虑非胶结充填体的侧压作用，对此，王瑞鹏等[11]、刘光生等[12]在此基础上考虑采充时序，研究了非胶结充填体侧压作用对胶结充填体稳定性的影响，修正了胶结充填体强度需求解析模型与方法。于永纯等[13]根据矿山实际岩石力学参数，通过数值模拟得到了一步骤胶结充填体的极限强度;刘光生等[14]利用数值模拟并结合搜索算法，得到了单侧揭露时胶结充填体的强度范围。以上研究表明，借助数值模拟手段可有效确定充填体强度设计范围。针对充填体结构及尺寸优化，邹南荣等[15]采用工程经验法和多种理论分析方法设计了高阶段充填体的强度，通过数值模拟进行验证，明确了矿房采场的充填分层高度;汪杰[16]考虑充填体分层结构，提出了分层充填体的强度计算模型，并结合数值模拟对充填体进行了结构与强度优化。上述研究主要集中于完整充填体的强度需求设计，并在此基础上进行结构优化，考虑充填体结构对强度的影响并进行强度及结构优化的研究涉及较少。

基于此，本研究基于力学计算模型对分层充填体所需强度进行分析，并通过室内力学试验研究充填体分层结构对强度的影响规律，最后采用数值模拟分析手段对高阶段嗣后分层胶结充填体的强度及结构进行优化，以确定合理的充填体分层结构及灰砂比参数。

1 高阶段嗣后分层胶结充填体强度需求分析

1.1 嗣后胶结充填体分层结构分析

采用阶段空场嗣后充填法开采的采场，将形成单个体积高达数万立方米的高阶段采空区。一次性完成整个空区的充填将会造成底部充填挡墙承受压力过大，存在一定的安全隐患;且大多数矿山由于充填站无法实现连续制浆导致难以一次性完成大体积空区充填。因此，现场通常采用分层充填方式(图1)进行，首先采用高灰砂比对承受压力较大的空区底部进行充填，将底层充填体养护到一定强度后，再进行中间层充填，最后采用高灰砂比对空区顶部进行充填，以承受来自顶板的压力，形成如图1所示的分层充填体结构。

1.2 充填体强度需求分析计算模型

图1 分层充填体结构示意Fig.1 Schematic of cut and fill body structure

针对单侧揭露充填体强度要求的问题，与经验类比及相似物理试验手段相比，通过力学模型能够更加简便有效地得到可靠、合理的结论。本研究充填体为分层结构，主要考虑分层结构面、滑动面及侧压作用对充填体强度的影响，为了快速评估一步骤采场充填体的稳定性，采用了基于采充时序的修正模型CM1[14]、考虑充填顺序与后壁黏结力的计算模型CM2[10]及考虑分层结构的计算模型CM3[16]3种计算模型(图2至图4)计算充填体所需强度。图2、图3、图4中h1、h2分别为顶底层、中间层高度，c1为顶、底层黏聚力，c2为中间层黏聚力，pb为非胶结充填体对胶结充填体的侧压力，S1为滑动面。

(1)基于采充时序的修正模型CM1。模型CM1考虑了非胶结充填体的侧压作用，适用于单侧揭露充填体强度计算。如图2所示，极限平衡状态下(安全系数F=1)，c1、c2计算公式为

图2 模型CM 1示意Fig.2 Schematic of CM 1model

式中，L为充填体揭露长度，m;B为矿体宽度，m;H为充填体揭露高度，m;φ为充填体内摩擦角，(°);α为潜在滑面与水平面的夹角，(°);x、y、z为计算系数，kN;r12为c1与c2的比值;H*为楔形体等效高度，m。

(2)考虑充填顺序与后壁黏结力的计算模型CM2。模型CM2兼顾了充填体的分层结构及滑动面位置对强度的影响(图3)，极限平衡状态下(安全系数F=1)，c1、c2计算公式为

图3 模型CM 2示意Fig.3 Schematic of CM 2 model

式中，Q为充填体滑动面处向下的竖向力，kN。

(3)考虑分层结构的计算模型CM3。模型CM3考虑分层结构的影响，对模型CM2进行了进一步修正。如图4所示，得出极限平衡状态下(安全系数F=1)，c1、c2计算公式为

图4 模型CM 3示意Fig.4 Schematic of CM 3model

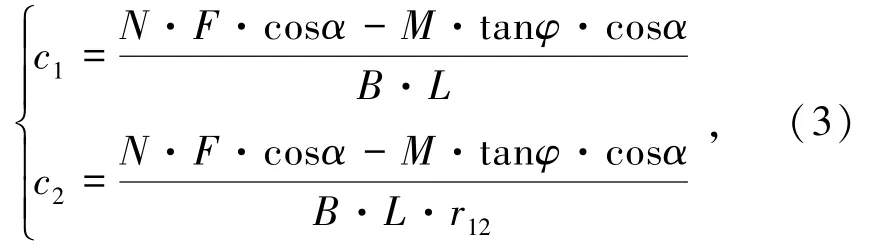
式中，M为垂直滑动面向下的合力，kN;N为沿滑动面向下的合力，kN。

1.3 分层胶结充填体强度需求分析

大冶铁矿矿岩岩性、结构复杂，-180～-270 m阶段采用分段凿岩阶段空场嗣后充填法开采，阶段高度H=90 m、矿房矿柱宽度B=15 m、长度L=25 m，采场底部需要留设高15 m的底柱，充填体实际高度75 m。参考文献[17]中的工程算例与充填体采矿实践，结合大冶铁矿充填体的相关力学研究结论，本研究计算参数[18]取值见表1。

表1 大冶铁矿分层胶结充填体强度需求计算参数Table 1 Strength requirement calculation parameters of the layered cemented backfill in Daye Iron Mine

表征胶结充填体强度需求的黏聚力c与其单轴抗压强度σ之间通常存在一定的比例关系(M=c/σ)。MITCHELL 等[7]、ARIOGLU[19]、ASKEW 等[20]根据试验得到M取值范围为0.1～0.2。参照前人研究，本研究M=0.2，在极限平衡状态(F=1)下，得到大冶铁矿分层胶结充填体强度需求计算结果见表2。

表2 大冶铁矿分层胶结充填体强度需求分析结果Table 2 Strength requirement analysis results of the layered cemented back fill in Daye Iron Mine

由表2可知:模型CM1认为滑动面S1处于底部位置，导致S1向下的合力较大，造成强度值σ1、σ2较大;矿山设计中需考虑S1的实际位置，避免得到的强度值过大，导致充填成本增加。模型CM3未考虑非胶结充填体产生的侧压作用，所得到的强度值σ1、σ2较小;实际生产过程中忽视侧向压力对于胶结充填体的影响，可能导致充填体发生失稳破坏，造成安全生产事故。模型CM2既考虑了侧压作用又考了滑动面S1的实际位置，得到的充填体强度理论值较为符合实际，考虑到顶层需要支撑顶板、底层充填体最先破坏，因此后文进行分析时，选用c1=350 kPa作为顶、底层充填体黏聚力的计算参数。

2 充填体分层结构对强度影响规律

2.1 试验方案

采用大冶铁矿全尾砂作为充填骨料，华重胶骨粉作为胶结剂。选取 1 ∶4、1∶6、1∶8、1∶10 的 4 组灰砂比，浓度65%，分别对4种灰砂比进行 1、2、3、4次充填制作标准充填体试件(图5)，分层高度随充填次数均分，养护28 d后(图6)采用电子压力试验机测试其单轴抗压强度。

图5 分次充填料浆Fig.5 Separate filling slurry

图6 养护完成的分层充填体试件Fig.6 Specimen of layered filling body after curing

2.2 试验数据分析

试验充填体单轴抗压强度取值见表3。根据表3绘制强度曲线，并对充填次数与分层充填体单轴抗压强度进行回归分析，得到不同灰砂比条件下的回归方程如图7所示，计算得到不同充填次数的充填体折减系数见表3。

表3 分层胶结充填体单轴抗压强度Table 3 Uniaxial compressive strength of layered cemented back fill

图7 单轴抗压强度拟合曲线Fig.7 Fitting curves of uniaxial compressive strength

综合分析表3、图7可知:

(1)不同灰砂比下，充填次数对分层充填体单轴抗压强度的影响规律基本一致，单轴抗压强度和充填次数之间呈二次方程关系，且相关性系数均大于0.996，拟合度较高。

(2)随着填充次数增多，强度值降低越大，充填体抗压强度弱化效应越明显，表明在一定范围内充填次数增加对充填体强度影响较大。

3 充填体强度与结构优化数值模拟研究

3.1 模型和参数

以大冶铁矿阶段空场嗣后充填开采为工程背景，构建的充填采场三维模型及结构如图8(a)和图8(b)所示，采用FLAC3D数值模拟软件结合搜索算法进行计算分析。矿岩均假设成各向同性且服从摩尔-库伦本构关系的结构体，物理力学参数取值见表4。一步骤采场分层胶结充填体和二步骤采场非胶结充填体均假设成服从摩尔-库伦破坏准则的弹塑性结构体，参数取值见表1。

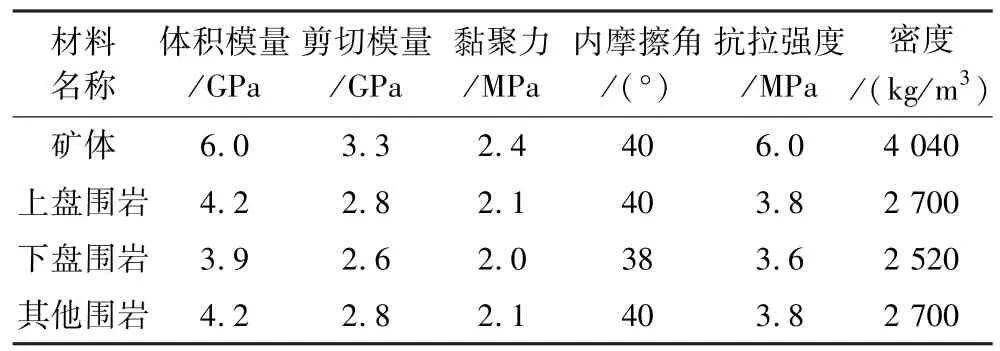
表4 数值计算模型材料参数Table 4 Material parameters of numerical calculation model

胶结充填体强度主要与其黏聚力有关[16]，在其他参数保持不变时，通过改变黏聚力c2值，计算分析极限平衡状态下(F=1)时中间层充填体的极限强度需求值σ2。根据2.3节分析结论，设置顶、底层充填体的黏聚力c1=350 kPa。寻优计算过程为:从初始值中间层充填体黏聚力c2=210 kPa开始，每次增加10 kPa进行寻优计算，直到二步骤回采结束后分层胶结充填体未发生贯穿式破坏时终止计算，此时得到的黏聚力c2即为中间层充填体所需黏聚力的极限值。数值模型布设两个监测截面，如图8(c)所示，通过两个监测截面上的塑性区发展与分布，判断一步骤矿房分层胶结充填体的稳定情况。

图8 三维模型及监测面Fig.8 3D model and monitoring surface

3.2 数值模拟结果分析

通过数值模拟分析得到两组具有代表性的模拟计算结果如图9所示。分析图9可知:

图9 采场充填体塑性图Fig.9 Plasticity diagrams of stope filling body

(1)中间层充填体黏聚力c2=270 kPa时，首次揭露时，仅在分层面(图9(a))上存在轻微的拉伸破坏，未发生沿滑动面贯穿式的剪切破坏，充填体整体处于稳定状态;再次揭露时，充填体沿滑动面发生贯穿式的剪切破坏(图9(b))，充填体失稳。整个开挖过程中，分层面上一直存在轻微的拉伸破坏，虽然首次揭露时未对充填体整体稳定性造成影响，但是再次揭露时，分层结构的存在加剧了剪切破坏程度，说明分层结构对于充填体的稳定性存在一定的影响。

(2)中间层充填体黏聚力c2=290 kPa时，再次揭露时，充填体沿滑动面发生剪切拉伸破坏，但是破坏未贯穿(图9(c))，且分层结构面上的拉伸破坏减少了，此时充填体处于稳定状态;说明随着中间层充填体强度的增加，分层结构面对充填体的影响相应降低。

(3)当中间层充填体黏聚力c2=290 kPa，取M=0.2时，中间层充填体强度c2=1.45 MPa。通过对数值解和理论解(F=1)对比分析可知，中间层所需强度数值解为1.45 MPa，小于理论解1.46 MPa，可取相对保守值1.46 MPa作为中间层胶结充填体所需强度。

3.3 分层胶结充填体结构优化

大冶铁矿-180～-270m阶段矿房回采结束后，采用如图10(a)所示的分层结构及灰砂比1∶4对空区进行充填，胶结剂消耗量大，充填成本居高不下。应在确保安全回采的同时，优化充填体分层结构及灰砂比参数，尽可能减少胶结剂的使用量，降低充填成本。

已有研究成果表明，现场胶结充填体强度通常为实验室测试结果的70%左右[16]。因此，根据前文对分层胶结充填体强度需求分析结果，对应室内试件中间层充填体所需强度为2.08 MPa，顶/底层充填体强度为2.50 MPa。由表3可知:灰砂比1∶6时，强度2.83 MPa能满足顶/底层充填体需求，灰砂比1∶8时，强度2.19 MPa可满足中间层充填体需求。因此从经济及强度需求角度考虑，可将图10(a)各分层的充填体灰砂比优化为图10(b)所示。由图9(b)和图9(c)可知:塑性区破坏主要发生在底部0～30 m处及顶部5m左右的区域，其他区域只存在轻微的塑性破坏。因此，可在图10(b)的基础上进一步优化，充填体最顶层5 m区域采用高灰砂比1∶6，往下区域可适当降低充填体强度，使用与中间层充填体相同的灰砂比 1∶8，如图 10(c)所示。

图10 充填体结构优化示意Fig.10 Schematic of filling body structure optimization

为验证优化后的充填体结构及强度的合理性，采用数值模拟方法对图10(c)进行分析，得到优化后的充填体塑性区分布如图11所示。可见，与图9(c)比，优化后的剪切破坏区域增大，但仍未发生贯穿破坏，高阶段嗣后分层胶结充填体能保持整体稳定，优化后的结构和强度可满足要求。

图11 矿房充填体结构优化及塑性区分布Fig.11 Structure optimization and plastic zone distribution of filling body in ore chamber

3.4 经济分析

根据矿山相关资料可知，在保证采场安全的前提下，对大冶铁矿高阶段嗣后分层胶结充填体强度及结构进行优化之后，可大幅减少胶结剂用量。如表5所示，以-270 m阶段2#矿房(25 m×15 m×75 m)为例，胶结剂减少量为2 206 t，减少率为40.2%，相应地充填成本降低了40.2%。

表5 技术经济指标对比分析Table 5 Comparision analysis of technical and economic indexes

4 结 论

(1)基于3种力学理论计算模型，分析了分层结构、滑动面位置及侧压作用对高阶段分层胶结充填体强度需求的影响。结果表明:滑动面位置不合理容易使充填体强度值偏大而导致充填成本增加，忽视侧压作用会使得充填体强度值偏小导致安全隐患，考虑了3种因素的计算模型(CM3模型)所得充填体强度理论值较为符合实际。

(2)通过室内力学试验研究了充填体分层结构对强度的影响规律，得到分层胶结充填体的单轴抗压强度和充填次数之间为二次方程关系，且在一定范围内，填充次数增多，强度值降低越大，充填体抗压强度弱化效应越明显。

(3)使用理论计算、FLAC3D数值模拟方法对大冶铁矿高阶段嗣后分层胶结充填体强度需求进行了计算分析。通过理论值及解析值的对比分析，得到顶、底充填体及中间层充填体的最小需求强度分别为2.50 MPa、2.08 MPa，并在此基础上进行了高阶段嗣后分层胶结充填体的强度及分层结构优化。在保证生产及采场安全的前提下，通过优化可大幅减少该矿充填体的胶结剂用量。