基于TensorFlow的手写体数字识别

高春庚， 孙建国

(济源职业技术学院 信息工程系， 河南 济源 459000)

0 引言

目前， 手写数字的识别是人工智能领域研究的热点， 其识别的方法有许多种， 如KNN(K近邻)、 支持向量机和神经网络等. 在模式识别和人工智能领域， 神经网络的应用非常广泛. 将神经网络应用于手写数字识别， 有识别速度快、 分类能力强、 容错性能和学习能力强等优点[1]. 本文将神经网络应用于手写体数字识别中， 结合了TensorFlow技术搭建神经网络模型， 并利用该网络模型进行手写数字的识别.

1 TensorFlow平台

Google的TensorFlow是一种用于解决机器学习问题的有效的方法. 其是一个开源的软件包， 该包的架构灵活， 可以运行在多种平台上[2]. 使用TensorFlow时， 主要采用计算图的形式. 计算图也叫数据流图， 其是一种有向图， 数学计算用节点和线来描述. 节点在数据流图中代表数学操作， 也可以表示数据输入的起点和输出的终点. 图中的线则表示节点间相互联系的多维数据数组， 即张量. 其描述了计算之间的依赖关系. 当输入端准备好张量数据后， 各种计算设备即可利用节点实现异步、 并行计算[3]. TensorFlow提供了搭建神经网络的接口， 利用这些接口可以方便地构建各种模型的神经网络， 从而可以简化编程过程[1].

利用TensorFlow平台通常需要以下步骤：(1)创建图. 所有的任务在TensorFlow中都需要转化为图的形式才能计算. 图包含了一组Operation代表的计算单元对象和Tensor代表的计算单元之间流动的数据.(2)创建会话. 创建的图要想传入TensorFlow引擎， 需要为该图创建一个会话.(3)启动图. 传入TensorFlow引擎的图需要启动后， 才能执行变量的初始化操作和其他操作.(4)结束会话[4].

2 神经网络

2.1 神经网络原理

人工神经网络(artificial neural network)是模仿自然界中动物大脑的结构和功能的一种计算模型. 该模型由许多神经元按照不同的层次组织起来， 按照从输入层到输出层进行前向运算， 前一层的输出加权求和后， 作为下一层的输入. 需要计算的数据通过输入层输入神经网络， 经过模型计算后的预测结果经过输出层进行输出. 然后把输出层输出的结果和真实的值对比， 并将误差反向传播， 之后不断调整神经网络的权重， 最终使网络的误差达到最小. 经典的神经网络结构包含三个层次， 分别为输入层、 输出层和隐藏层. 如图1所示.

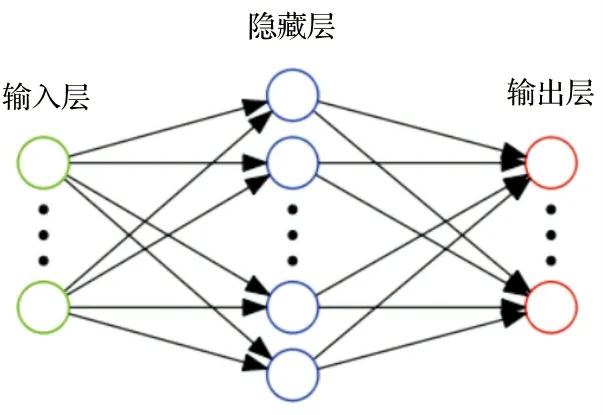
图1 神经网络模型图

网络中每层的圆圈代表一个神经元. 隐藏层和输出层的神经元由输入的数据计算后输出， 输入层的神经元只是输入. 神经网络中每个连接都有一个权值， 同一层神经元之间没有连接.

神经网络的主要用途在于分类. 利用神经网络处理多分类问题时， 假如有n个类别， 通常神经网络的输出节点也设置为n个.

2.2 Softmax回归

Softmax回归模型是一种解决多分类问题的模型， 是从解决二分类问题的logistic模型演变而来. 假设数据集由{(x1,y1), (x2,y2), …(xn,yn)}共n个样本组成， 其中xi为输入特征，yi为目标值. 在多分类问题中，yi的取值有多个组成.Softmax回归模型将神经网络输出结果yi转换成概率结果. 如图2所示：

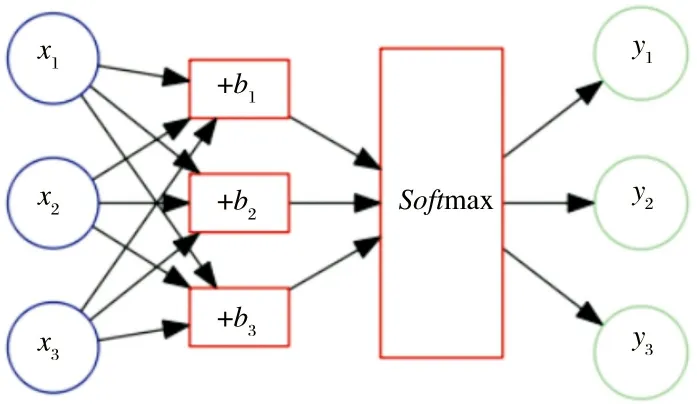
图2 Softmax回归模型图

假设神经网络的权重为wi,j， 则图2用矩阵的形式描述为[4]：

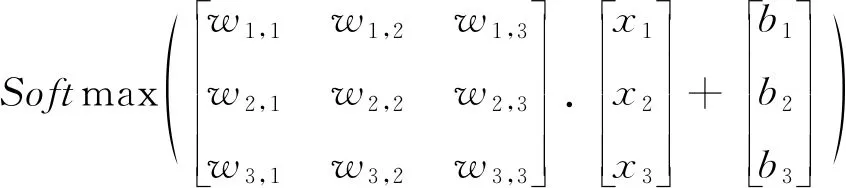
(1)

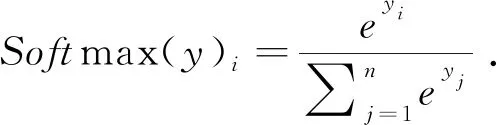
当数据通过输入层输入神经网络后， 通过公式(1)计算， 预测出各个样本属于某个类别的概率值， 并根据概率值大小对样本进行分类.

3 基于TensorFlow的模型实现

3.1 MNIST数据集介绍

本实验采用MNIST数据集. 该数据集包含很多图片， 其被分成了训练数据集和测试数据集两部分. 其中训练数据集(mnist.train)共包括55 000行数据， 测试数据集(mnist.test)共包括10 000行数据. MNIST数据集中的每个样本都包含两部分：第一部分是一张图片， 该图片包含手写数字;另一部分是该数字对应的标签. 每张图片都是黑白图片， 为28×28像素[5]. 如果将该数组以向量的形式展开， 其长度则是28×28=784. 每个样本都具有相应的标签， 用one-hot编码表示样本图像中绘制的数字. 例如[0,0,0,0,0,0,1,0,0,0]表示数字8[6].

3.2 模型实现

神经网络输入层. 由于输入的图片共28*28=784像素， 而且是黑白图片， 通道数是1， 所以每个样本一维化后输入的特征值共784个， 一张图片输入时输入层需要784个神经元.

x=tf.placeholder(dtype=tf.float32,shape=(No,784)). 代码中No代表输入图片的张数.

神经网络的输出层是Softmax回归模型， 因为目标值0～9共10个数值， 所以输出层用一个1*10维张量来表示10个类别.

y_true=tf.placeholder(dtype=tf.float32,shape=(No,10)). 这里的No与神经网络的输入对应， 也代表输入图片的张数.

因为输入的图片共784个特征， 目标值共10个类别， 即目标值共10列， 所以神经网络的权重值w(用矩阵表示)的形状为784*10. 进行加权求和时， 加上偏置量， 最后通过Softmax映射， 以实现对数字的分类.

Weights=tf.Variable(initial_value=tf.random_normal(shape=[784,10]))

bias=tf.Variable(initial_value=tf.random_normal(shape=[10]))

训练阶段. 损失函数用交叉熵损失和Softmax结合， 用梯度下降法优化损失.

4 实验结果与分析

在人工神经网络训练的过程中， 迭代次数和学习率对结果有很大的影响. 目前还没有有效的方法设置迭代次数和学习率， 一般是通过多次实验来调整学习率和迭代次数， 从而得出模型参数.

当学习率设为0.05时， 损失随着训练次数的增加不断减小， 训练次数接近300次时， 损失降到1.2左右， 准确率到达80%， 如图3、 图4所示； 当学习率为0.1时， 随着训练次数的增加， 损失越来越小， 训练次数接近280次时， 损失降到0.19左右， 准确率达到99%， 如图5、 图6所示. 因此学习率设置为0.1， 迭代次数为280时， 准确率已收敛， 无需再进行更多次数的训练.

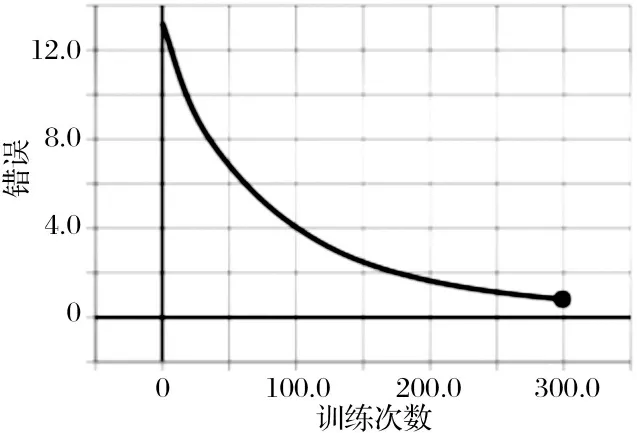
图3 学习率为0.05时损失率变化曲线

图4 学习率为0.05时损失和准确率

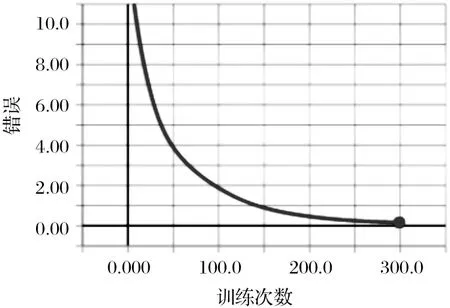
图5 学习率为0.1时损失率变化曲线

图6 学习率为0.1时损失和准确率

5 总结

本文介绍了一款基于TensorFlow的手写体数字识别的设计与实现过程. 其基于人工神经网络原理， 用TensorFlow搭建神经网络并进行训练， 并用MNIST数据集进行实验， 识别较为准确. 当然， 本方法还有待改进的地方， 由于实验所使用的计算机性能有限， 本文只设计了3层神经网络， 下一步研究将增加网络层数、 用更好的算法优化以减少损失等.