化归思想在高中数学解题中的应用

江苏省句容市实验高级中学 郝荣春

化归思想是指在主体原有知识、经验、理解、思考的基础上，将未知的、较为困难的问题转化为已知的、简单的、容易解决的问题，它是数学思想中的重要组成部分。在核心素养培养视角下，教师应注重渗透化归思想，让学生提升思维模式，掌握数学知识和解题技巧。

一、化归思想的基本内涵与思想核心

在数学发展的历史中，每一个公式或定理的发现与提出背后都有一种数学思想作为支撑。因此，在素质教育以及核心素养视角下培养新时代高中生的数学能力与解题能力，需要教师培养学生的数学思想，让学生懂得数学的本质，并做到举一反三，使问题迎刃而解。

化归思想的核心就是转化与归纳，借助一定的方法、手段将复杂、困难的问题简单化，将不会的题目转化成会的、已经学习过的知识，将信息量大的未知题目用自己掌握的知识体系分解，通过变换角度思考问题找到解题思路。

高中数学题目侧重对知识运用能力与知识点掌握的考查，化归思想可以帮助学生快速找到解题思路，将当下问题转变成数学模型或简单公式，在原有知识基础上构建自己全新的知识体系，提升学习效率，因此化归思想在高中数学解题过程中有很大作用。

二、化归思想在高中数学中的实际应用

（一）提升逻辑思维

在函数以及不等式等模块的学习中，教师应当培养学生的化归思想与逻辑思维，如“要想……首先需要……然后……”的思路，从而带动学生分析与解答数学题。

例如，在苏教版《基本不等式》的学习过程中，学生经常遇到不等式与函数相结合的题目：

已知：a，b∈R，求证：｜a｜+｜b｜／1+｜a｜+｜b｜＜｜a+b｜／1+｜a+b｜

分析：这道题表面上看是不等式的求证问题，实际上是考查函数的单调性问题。因此，教师可以引导学生将题目转化为函数在区间内的单调递增或递减问题来进行求证。

证明：设f（x）＝x／1+x，x∈［0，+∞）

x1，x2是x∈［0，+∞）上的任意两个实数且0≤x1＜x2，则f（x1）-f（x2）＝x1／1+x1-x2／1+x2＝x1-x2／（1+x1）（1+x2）

∵0≤x1＜x2，∴f（x1）＜（x2）

∴f（x）＝x／1+x在x∈［0，+∞）上是增函数（大前提）

∵｜a｜+｜b｜≥｜a+b｜≥0，可知f（|a|+|b|）≥f（|a+b|）。

以上可以看出，掌握了数学化归思想，就能让未知的、看起来复杂又难以解答的问题转化成已知的、熟悉的，并能通过运用基础知识解答的问题，使题目变得简单。

（二）运用数形结合

其实数形结合的理念在小学以及初中的数学学科中就有渗透：鸡兔同笼、植树问题、简单函数等，都是数形结合的运用以及渗透。数形结合能帮助学生更好地掌握数学知识，形成系统的思想模块，通过将抽象的问题具象化，通过动手与实践能力的培养，让学生掌握问题的解决办法。

高中数学更加抽象化、复杂化，在解题过程中，学生会抓不住解题方向与思路。随着对数学知识不断深入的学习，学生的认知结构与思维方式会更加成熟，学会运用化归思想，通过数形结合的方式来学习数学知识、总结解题思路，能用辩证的视角看待问题、解答问题。

例如，苏教版《三角函数》涉及的符号、概念、公式都比较抽象，在学习过程中教师就可以引导学生利用数形结合的方式，快速找到解题思路，并将难以理解的抽象概念变成实际操作。

解答：依题知，点（2cosx，4sinx）在轨迹方程的椭圆上。

因sinx2+cosx2＝1，所以题中所求值域就是椭圆上的点和点（4，-1）连线的斜率。设切线方程为y+1＝k（x-4），将其与椭圆联立，得判别式为0，

即4x2+［k（x-4）-1］2＝16

（4+k2）x2-（8k2+2k）x+16k2+8k-15＝0［-（8k2+2k）］2-4×（4+k2）（16k2+8k-15）＝0 12k2+8k-15＝0

（2k+3）（6k-5）＝0

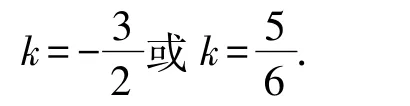
对这类问题，教师在课程安排中要引导学生进行联想与思考，在学习新知识的过程中利用与复习以往知识，从而让学生形成自己的解题思路与逻辑体系。

（三）简化转熟原则

教师在教学中应注重学生数学素养的培养，不要将学生的考试成绩作为教学的唯一目的，要培养学生对数学的探索精神，注重化归思想在数学学科内的应用。

例如，在苏教版《等比数列》的教学过程中，很多教师会觉得等比数列的题目较为容易，即便学生不会推理演算，也可以通过列举选出对的结果。但是这种教学思路与素质教育相违背。核心素养视角下要求高中数学教学“注重提高学生的数学思维能力”，通过“直观感知、观察发现、归纳类比、空间想像、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等形成思维过程”。

例如，是否存在一个等差数列｛an｝，使得对任何自然数n，等式a1+2a2+3a3+…+nan＝n（n+1）（n+2）都成立，并证明你的结论。

分析：教师可以先引导学生进行简单思考，通过对问题的认知与把握将其变得直观化，利用特殊性与一般性、复杂化与简约化的思想理念，将问题分解开，在矛盾中分析问题，再通过系统分析总结出一般结论。

解：将n＝1，2，3分别带入等式可得：

a1＝6

a1+2a2＝24

a1+2a2+3a3＝60

解得a1＝6 a2＝9 a3＝12

故存在一个等差数列an＝3n+3，当n＝1，2，3时，等式成立。

接下来教师可以利用数学归纳法引导学生掌握解题思路，只要将原有的复杂问题转化为简单的问题：证明存在一个等差数列an＝3n+3，对大于3的自然数，a1+2a2+3a3+…+nan＝n（n+1）（n+2）都成立。

解：假设n＝k时，等式成立，

即a1+2a2+3a3+…+kak＝k（k+1）（k+2）

当n＝k+1时，有a1+2a2+3a3+…+kak+（k+1）ak+1

＝k（k+1）（k+2）+（k+1）［3（k+1）+3］

＝（k+1）（k2+2k+3k+6）

＝（k+1）（k+2）（k+3）

＝（k+1）（（k+1）+1）［（k+1）+2］

因此当a＝k+1时也存在一个等差数列an＝3n+3

使a1+2a2+3a3+…+nan＝n（n+1）（n+2）成立。

教师在讲解题目的过程中，应注意把握学生的学习心理，让学生简化做题思路，通过化归思想进行规律总结与认知，从而增进对知识点的掌握程度。

三、化归思想对高中数学的积极影响

事物的普遍规律是发展变化，矛盾常常伴随事物发展的整个过程，并不断产生联系。学生在学习高中数学的过程中也会不断遇到已知与未知、熟悉与陌生、简单与复杂的问题，而化归思想就是将事物不断进行转化与归纳总结的过程。这种学习思路不仅让高中数学学习变得简单有条理，而且能让学生掌握举一反三的学习方法，有助于数学核心素养的培养。

四、结语

在高中数学的教学过程中，教师应当注重对学生整体素质的培养，化归思想的普及以及理念渗透法对教师来讲是一种易于使用的教学策略，对学生来讲也是非常实用的学习手段与解题思路，因此在高中数学课堂教学中渗透化归思想极为重要。