基于雷诺数的大气阻力模型在飞行器再入预报中的应用*
2022-04-13刘劲宏徐劲杜建丽潘建平
刘劲宏 徐劲 杜建丽 潘建平
1(中国科学院紫金山天文台 南京 210023)
2(重庆交通大学智慧城市学院 重庆 400074)
0 引言
大气再入预报是指目标从当前轨道高度自然衰减到120 km 所需时间。大气再入分为两类,即受控再入和无控再入。受控再入以偏远地区为目标,对地面威胁最小,而无控再入受多种因素影响,其预报的坠落时间、地点具有随机性。部分目标结构坚固、耐高温,在大气再入过程中难以烧蚀和解体,对地面人员和财产安全构成潜在威胁。Pardini等[1]统计了2008-2017年完整航天器无控再入数量与质量的分布,共计448 个,总质量约900 t[1]。统计数据表明:过去10年内,平均每周至少有一个完整的飞行器(卫星、火箭体和运载平台)重返大气层,平均质量约2 t,导致每年有50~100 t 的完整飞行器重返大气层。随着巨型卫星星座的布设及碎片主动移除技术的论证与实现,未来再入事件的发生频率将更高且质量更大,对人类空间活动及地面安全构成的威胁与日俱增。为此,亟需对在轨的大型航天器进行监测、跟踪和预警,以应对可能出现的紧急突发情况。
STK(Satellite Tool Kit)提供多种轨道预报模型,可选择模型包括:TwoBody、J2 Perturbation、J4 Perturbation、HPOP(High Precision Numerical Orbit Propagator)等。本文选择高精度数值轨道传播器HPOP[2-4]和中国武汉大学提出的半解析轨道传播器WHU-SST(Wuhan University Semi-Analytical Satellite Theory)[5]对低轨道目标,特别是临近大气层的目标进行再入预报。HPOP 采用COWELL 数值方法对力学模型进行积分,WHU-SST 是基于多尺度摄动理论的半解析轨道传播方法,其核心思想是将轨道根数分为长周期变量和短周期变量,采用数值积分方法对目标的平均轨道根数进行大步长积分,利用解析算法重建短周期项,最后对计算得到的平均轨道根数和短周期项重组,获得快速、精确的轨道。为便于后续分析讨论,对以上两种轨道预报模型设置相同的参数,采用Runge-Kutta-Fehlberg 7(8)积分,引力选择JGM3 和70×70 阶次,太阳辐射压为球形,大气密度模型选用NRLMSISE-00,大气阻力系数CD=2.2,第三体引力考虑太阳和月球。
对于低轨目标的轨道预报,大气阻力系数模型是影响再入大气预报精度的关键。实际应用中,大气阻力系数以三种方式取值,即常数值、拟合值和物理值[6,7]。一般轨道传播器的大气阻力系数采用常数值,通常设置为2.2,然而其不能反映目标阻力系数的真实情况,使得计算的大气阻力存在很大偏差[7]。拟合大气阻力系数通过轨道确定获得,与选择的大气模型相关,同时也会吸收其他模型的误差[8]。物理大气阻力系数反映了航天器表面与自由分子流的能量和动量交换,主要受到覆盖在航天器表面的氧原子吸附影响[9],其数值精确,但是计算量大且耗时长。
事实上,已有较多研究者在实验室通过模拟大气环境获得不同形状、纵横比的大气动力经验系数。针对纵横比近似3∶1 的圆柱体飞行器,本文在简化飞行器模型的基础上引入基于雷诺数的大气动力系数经验模型,采用RK6 (7)对运动方程重新积分,探讨该模型用于火箭体再入预报所需条件,为后续研究奠定基础。该模型能够同时考虑大气阻力和升力的影响,适用雷诺数范围为10~300[10]。
1 大气动力模型
通常临近大气层的飞行器,其大气阻力系数变化剧烈,可引起极大的预报误差(见图1)。在再入前的第10 天左右,飞行器运行高度开始陡然下降,表明大气阻力系数取常数值或拟合值均不能真实模拟飞行器再入轨迹的改变。因此提出了基于雷诺数的大气动力系数经验模型。
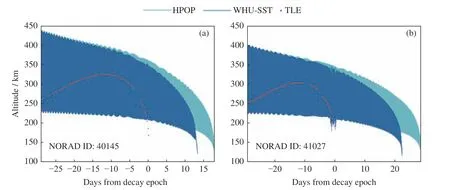
图1 火箭体40145 和41027 再入过程中的高度变化Fig.1 Altitude changes with time during the objects of 40145 and 41027 reentry atmosphere
雷诺数是用于表征流体流动状态的无量纲数,其定义如下:
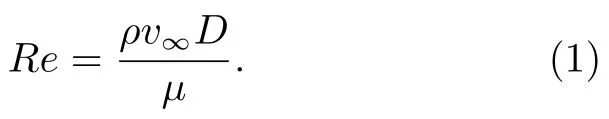
式中:ρ为流体密度,由NRLMSISE-00 大气密度模型计算得到;v∞为自由流速度;D为等效球体直径;µ为流体动力粘度系数。
为评估圆柱体受到的大气阻力大小,Cao等[10]建立了基于雷诺数的阻力系数和升力系数表达式,讨论了其随流体入射角的变化。假定流体入射角为θ,则阻力系数CD,θ和升力系数CL,θ的计算公式如下[10]:
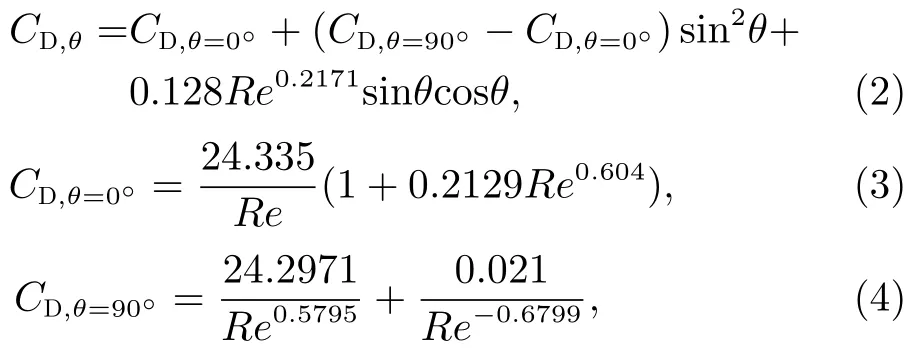
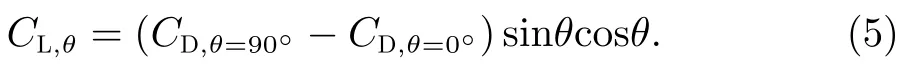
式(2)~(5)适用的雷诺数范围为[10,300]。实验表明:阻力系数平均相对误差为1.5%,均方根误差为1.5×10−3;升力系数平均相对误差为5.77%,均方根误差为1.9×10−3[10]。
假定火箭体的长度为L,直径为D,则投影到入射流方向的面积可表示为
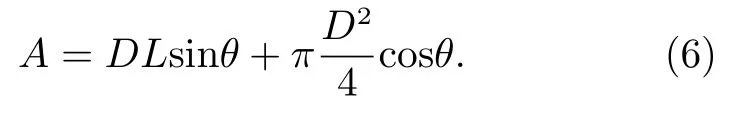
假定质量为m,弹道系数(Ballistic Coefficient,定义数学符号CB)可表示为

假定火箭体和残存燃料质量共10 t,利用式(2)~(5)、式(6)和式(7)计算不同雷诺数下弹道系数随入射角的变化情况,如图2 所示,雷诺数变化范围为[10,300]。从图2 可以发现,尽管雷诺数不同,但是弹道系数随入射角变化的峰值都在75°~80°内,四幅图的变化趋势完全一致,受火箭体尺寸影响,纵轴变化范围有所不同。
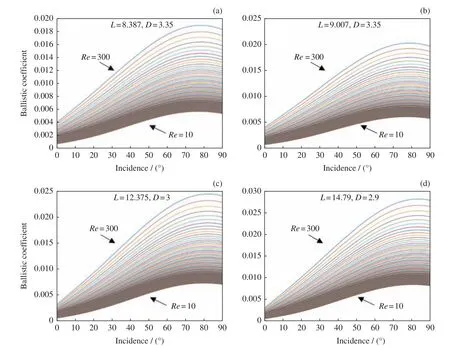
图2 不同纵横比的弹道系数随入射角度的变化Fig.2 Variation of ballistic coefficient with incident angle for different aspect ratio
2 火箭体长时间再入预报
火箭体的大气再入过程具有如下特点:历史再入数量多、质量大、频率高且难烧蚀,结构保持完整。这里主要讨论的对象为中国航天发射活动使用的长征系列运载火箭体。表1 给出了部分二级火箭体的尺寸和质量,以便估算与大气阻力相关的物理参数,其中定义等效球体直径为与火箭体体积相同的球体直径*http://cn.cgwic.com/LaunchServices/LaunchVehicle/LM3 B.html。

表15 种长征系列火箭体的二级火箭尺寸和质量Table 1 Size and mass of two-stage rockets of five kinds of Long March series rocket carriers
假定火箭体在再入大气层之前已处于长时间稳定状态,即姿态稳定、质量稳定,此时面质比及受到的流体入射角度应为常量。基于此,如何利用历史TLE 数据确定合适的面质比和入射角,是采用基于雷诺数的大气动力模型精确预报火箭体再入的关键。这里主要讨论时间长度为一个月的再入预报。
在飞行坐标系下,大气摄动加速度采用下式描述:
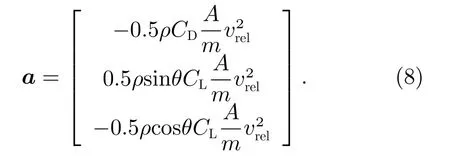
加速度的矢量方向分别为速度方向(阻力方向)、垂直于速度向上的方向(升力方向)以及与这两个方向相互垂直的方向。其他摄动力包括EGM2008 20×20阶引力场、太阳辐射压、第三体(日、月)引力,大气密度模型选用NRLMSISE-00 模型。采用RK6 (7),即Runge-Kutta-Fehlberg 6 (7)对轨道运动方程以固定步长(10 s)向前积分,获得再入时间的预报。
预报采用百分比误差,其定义为[11]
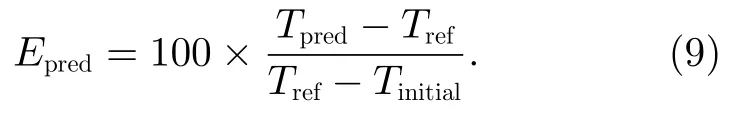
式中,Tref为真实再入时间,Tpred为预报再入时间,Tinitial为预报的起始时刻。
收集2000年以来再入的火箭体数据,剔除因观测值稀少及质量不佳的某些火箭体,经过数据质量清理、弹道系数估计和轨道定轨,获得5 种火载体共计26 个预报结果,其中:CZ-4B R/B 12 个,CZ-3B R/B 6 个,CZ-2C R/B 5 个,CZ-2D R/B 2 个,CZ-3C R/B 1 个。图3 为5 种火载体在入射角变化范围为[1°,90°]时再入前30 天的预报结果。可以看出,随着入射角的增加,大气阻力系数越大,预报的再入时间越短。图3(f) 给出了26 个火箭体再入预报误差分布,流体入射角为12°。
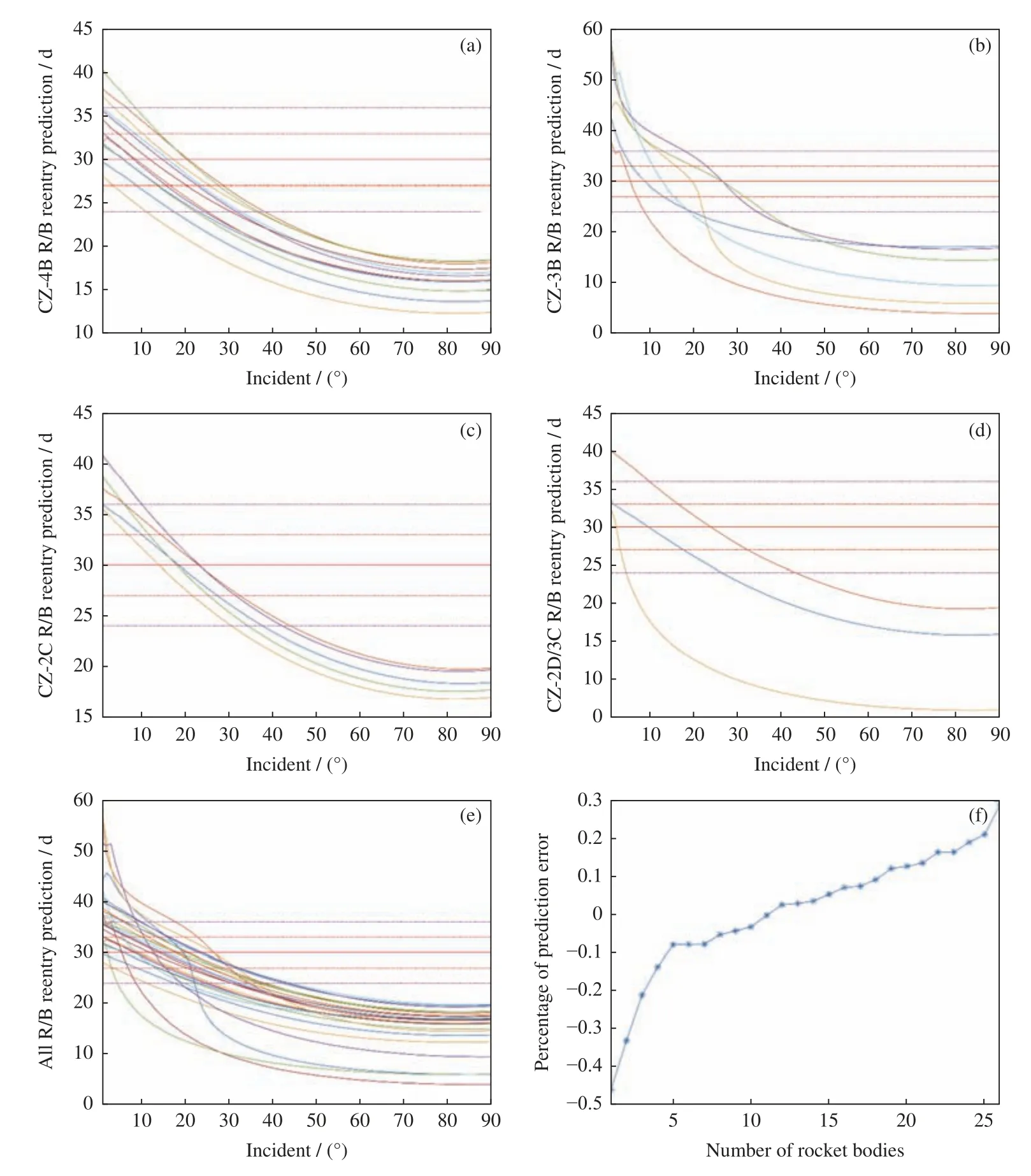
图3 入射角对火箭体再入预报的影响和入射角为12°时火箭体的预报误差百分比(红色实横线是预测误差为0 的基线,即第30 天结果,红色点线为预报误差±10%的范围线,品红点线为预报误差±20%的范围线)Fig.3 Influence of the incident angle on the reentry prediction of the rocket body and the prediction error percentage of the rocket body when the incident angle is 12° (Red solid line is baseline with 0 prediction error,the red dotted line deviates ±10% from the baseline,and the magenta dotted line deviates ±20%)
已知实际再入时间在第30 天。因此,CZ-4B 火箭体对应的入射角应在10°~20°内,CZ-3B 火箭体对应的入射角在10°~30°内,CZ-2C 火箭体对应的入射角在12°~24°内,CZ-2D 火箭体对应的入射角在10°~23°内,CZ-3C 火箭体的对应的入射角在2°~3°内。通过分析,先验入射角范围为12°~14°,可以使得84.62% 的火箭体再入时间预报误差小于20%,53.84%的火箭体预报误差小于10%。
为了与高精度数值轨道传播器HPOP 和半解析轨道传播器WHU-SST 的预报结果进行比较,选择8 个火箭体作为目标。表2 列出了8 个目标的轨道信息和预报误差。WHU-SST 的预报误差整体比HPOP预报误差低30% 以上,而新模型的预报误差最高为16.1%,远小于WHU-SST 的最高预报误差83.61%。因此,利用基于雷诺数的大气阻力模型不仅能够有效降低再入预报误差,还可以提高预报成功率。
需要说明的是,表2 中目标40550 属于地球同步转移轨道目标,而本文使用的基于雷诺数的大气模型仅适用于200 km 左右高度的火箭体目标,因此没有进行再入预报计算。
3 在陨落位置预报中的应用
将基于雷诺数的大气阻力系数模型应用于陨落预报,即高度范围为10~120 km。目标22659、24770、25240、26607、38086 和41107 已坠落于地球表面,图4 中黑色三角形为残骸找到的真实位置,这里将其作为陨落位置,红色点为陨落预报位置。陨落预报考虑了定轨误差和大气密度模型误差,因此呈现散点分布。本文基于TLE 数据进行陨落预报,仅能实现实际陨落位置位于预报散点中的某一点。图4 所列6 个目标(形状仅包括球体和圆柱体)的陨落位置预报受各种误差影响,呈现散点或者近似多条曲线分布,真实陨落位置位于其中的预报轨迹中。
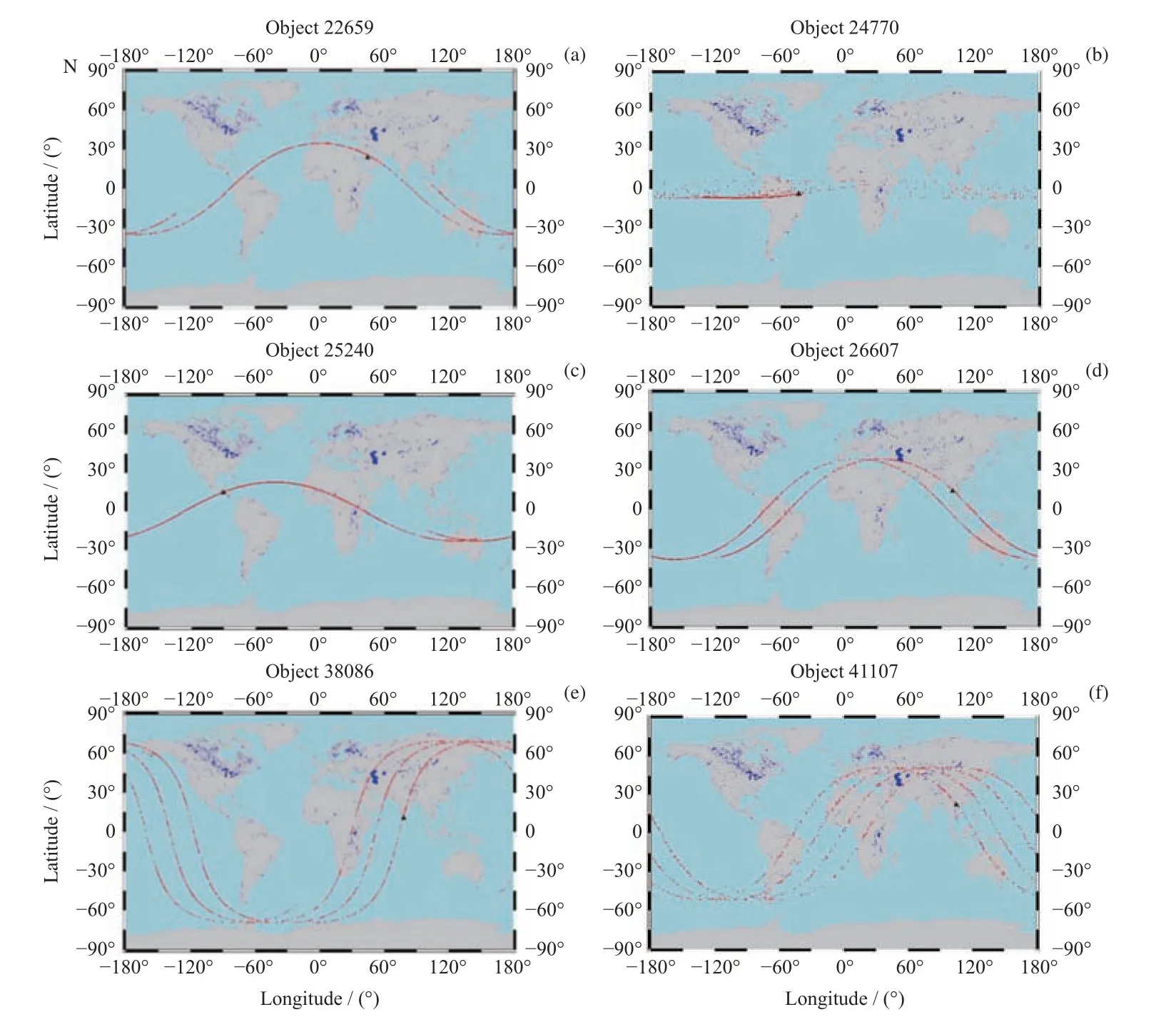
图4 基于雷诺数的大气阻力系数模型的陨落预报位置分布(黑色三角形为残骸找到的真实位置,这里将其作为陨落位置;红色点为陨落预报位置)Fig.4 Distributions of decayed locations predicted by new atmospheric drag coefficient model based on Reynolds number (Black triangle is for the real falling location and the red dot is for the falling location of prediction)
4 结论
针对现有轨道传播器对低轨目标大气阻力系数描述不准确的问题,在简化航天器模型的基础上,引入基于雷诺数的大气动力系数经验模型,确定了适用于低轨火箭体的最佳流体入射角,重新对运动微分方程进行轨道数值积分,所获结果与现有轨道传播器的预报结果进行对比,结论如下。
(1)与已有的轨道传播器相比,基于雷诺数的大气阻力系数模型在中国火箭体的再入预报方面具有明显优势,预报误差显著降低,预报成功率上升。例如目标41027 的预报误差从75%~96%下降至7.6%,目标38253 和40120 预报成功。通过6 个目标的陨落位置预报,能够确保真实陨落位置位于预报的统计陨落位置中,间接证明了基于雷诺数的大气阻力系数模型的有效性。
(2)基于雷诺数的大气动力系数模型虽然在火箭体的预报中取得了较好的预报结果,但是受限于雷诺数的应用范围,该模型不适用于地球同步转移轨道目标的再入情况。由于收集到的火箭体数量有限,未对再入预报进行外推核验。未来会利用新的再入火箭体,验证基于雷诺数的大气动力系数模型的可靠性。
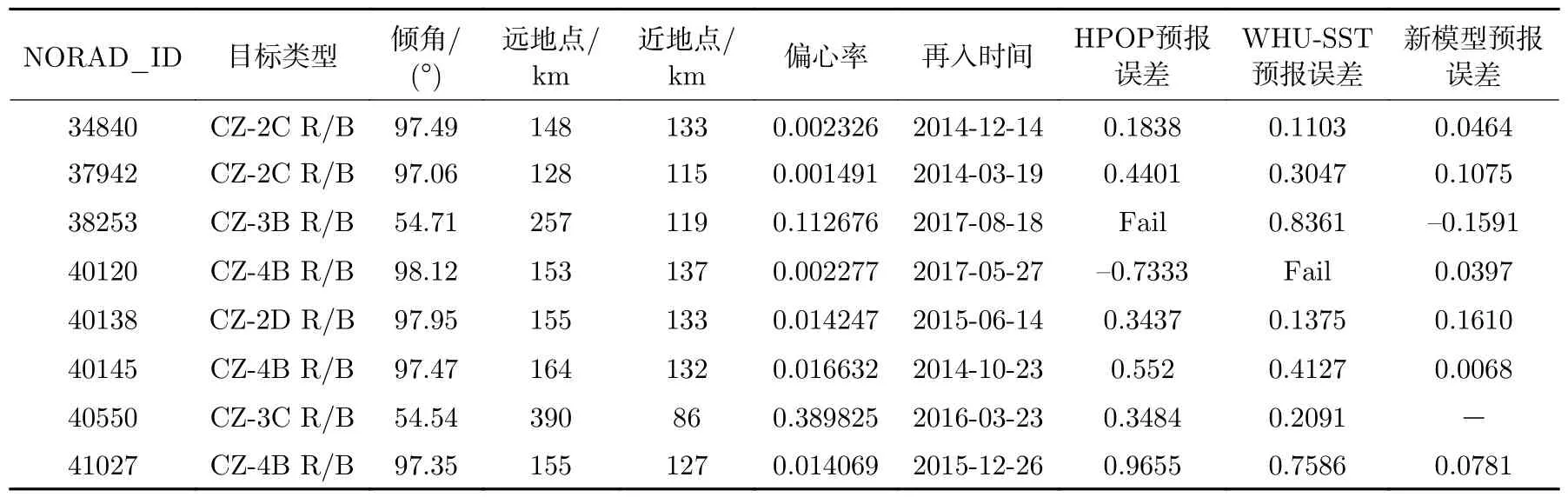
表28 个火箭体轨道信息和预报误差Table 2 Orbit information and prediction errors of 8 rocket bodies
