ARIMA-SVR 组合模型在卫星遥测参数预测中的应用*

顾昕雨 肖志刚

1(中国科学院国家空间科学中心 北京 100190)

2(中国科学院大学 北京 100049)

0 引言

卫星在轨运行过程中，空间天气、温度、光照等外部因素均对其运行环境造成一定影响，导致卫星各部件性能随外部环境改变而发生一定变化。这些变化可能会使卫星在运行过程中出现故障，造成不可挽回的事故损失。卫星在轨运行过程中会生成大量遥测数据，这些数据能够直接、客观反映卫星各部件的工作状态，是预测及处理卫星故障的重要基础[1]。为了提高卫星在轨运行的安全性，降低卫星运行中存在的风险，研究者提出了不同的方法，预测飞行器遥测数据的变化趋势，并通过真实数据与预测数据趋势的对比，及时发现数据异常。

卫星遥测数据会随着时间变化，因此一定程度上可以视为时间序列。结合中国科学院先导专项卫星的实际遥测数据，可将遥测参数大致分为三类：第一类是平稳性遥测参数，随时间变化缓慢；第二类是突变型遥测参数，随时间呈跳跃性变化；第三类是周期性遥测参数，随时间呈周期性变化[2]。针对不同环境的数据预测有研究提出了不同的方法。Zhang等[3]通过人工神经网络（ANN）对非线性时间序列数据进行预测，验证了神经网络对非线性时间序列数据的处理优势；在神经网络基础上，有研究提出了优化算法与神经网络相结合的组合模型，例如Donate等[4]提出了遗传算法与神经网络相结合的模型，并通过实验证明了该模型在时间序列预测中具有一定优势；Zhu等[5]将LSTM 用于卫星轨道预报，证明LSTM 在遥测时序数据处理方面有一定作用；Ren等[6]通过马特拉小波变换算法对卫星太阳翼输出功率进行短期预测，提高了对具有非平稳及周期性数据特性的遥测数据的预测精度。

除此之外，在卫星遥测数据预测领域，常用的预测算法还有自回归移动平均模型（ARMA）。Yu[2]验证了ARMA 的适用性。ARMA 模型的验证表明其更适用于平稳数据的预测，但是卫星遥测数据具有非线性、周期性、不平稳等特点，单一的ARMA 模型不能精确预测卫星遥测数据。针对时间序列数据不平稳的特点，ARIMA 模型可以对其差分使得时间序列变为平稳序列，但是对于时间序列存在的非线性特征不能充分处理。SVM 模型作为机器学习中的常用模型，在预测研究中具有良好的泛化性能，SVM 用于回归问题时即为SVR。Liu等[7]利用SVR 对光伏发电功率进行残差修正，提高了预测精度。

基于卫星遥测数据的特点，本文将ARIMA 预测模型与SVR 预测模型相结合，利用ARIMA-SVR 组合模型对卫星时序遥测数据进行短期及中期预测，通过与单一ARIMA 模型的预测结果进行比对，验证组合模型在时序遥测数据预测中的适用性，为卫星正常在 轨运行管理提供决策分析技术支持。

1 研究方法

1.1 ARIMA 模型

ARIMA 模型全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model)。ARIMA 模型的基本思想是，利用时间序列自身的滞后序列和随机扰动项及其滞后序列，描述时间序列发展规律[8]。ARIMA(p,d,q) 包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)和自回归滑动平均混合过程(ARIMA)。该模型的一般形式为

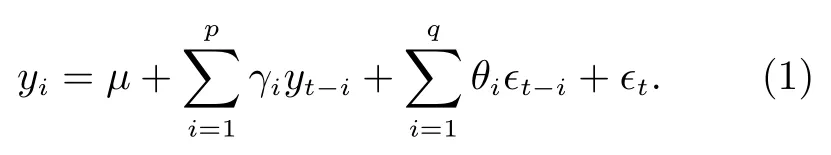
其中：µ为常数系数；p为自回归阶数；q为移动平均阶数；ϵt为随机误差，通常是白噪声序列，且符合正态分布；γi和θi为待求参数。对于非平稳序列，先对其进行d阶差分获得平稳序列，再进行建模。

1.2 SVR 模型

支持向量机（SVM）是基于统计学VC 维理论和结构风险最小化理论建立的机器学习算法[9]。当SVM 应用于回归问题时即为支持向量回归（SVR），给定非线性数据集{xi,yi}，其中xi为样本输入，yi为样本输出，将样本从低维空间直接映射到更高维的特征空间，φ(xi)表示xi映射后的特征向量[10]。超平面公式如下：

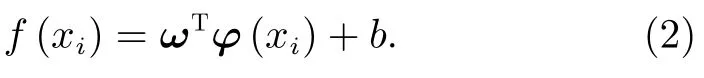
其中ω,b均为待定参数。传统模型中认为f(xi)与yi完全重合时才是最佳模型，此时损失计为零。但SVR模型允许f(xi)与yi之间最多有e的偏差，即当f(xi)与yi之间差的绝对值大于 2e时才计入损失，即训练样本落入以f(xi)为中心的 2e宽度带内时则认为训练正确[11]。训练SVR 的过程实际就是寻找最优的ω和b使f(xi)逼近yi[10]。此时ω和b的求解可以视为一个凸二次规划问题，即

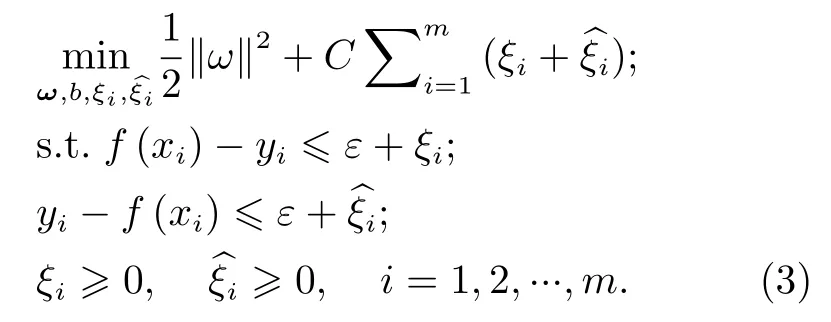
其中，ξi和为松弛变量，ε为f(xi)与yi之间的偏差，C为正则化常数。ω可表示为

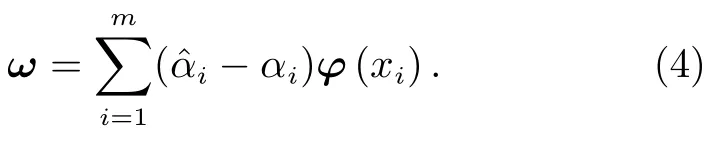
则所求SVR 的回归模型为

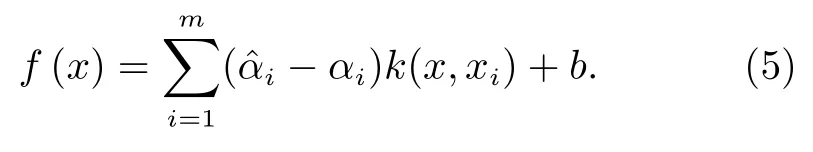
其中k(x,xi)为核函数。

2 基于ARIMA-SVR 组合模型的预测方法

卫星遥测数据是连续变化的时间序列，ARIMA模型可以较好地体现时间序列中的线性特质。由于运行环境等因素的影响，时序遥测数据体现出一定的非线性特征，而SVR 方法适用于非线性特征的映射。因此本文利用ARIMA-SVR 组合模型对时序遥测数据进行预测，具体流程如图1 所示。

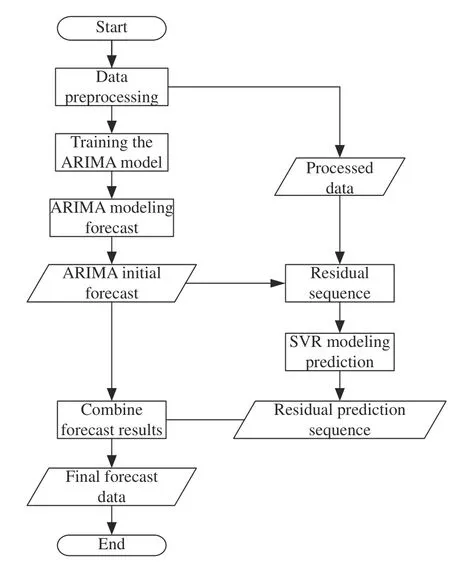
图1 基于ARIMA-SVR 组合模型的卫星遥测数据预测建模流程Fig.1 Modeling process of satellite telemetry data prediction based on ARIMA-SVR combination model

ARIMA-SVR 组合模型的预测首先对数据进行预处理，处理后的训练集作为ARIMA 模型的输入，ARIMA 建模预测获得初始预测结果，原始数据与ARIMA 预测值的残差作为SVR 模型的输入，再将SVR 预测的残差值与ARIMA 预测初始值相加得到最终预测结果。具体过程如下。

（1）数据预处理。卫星在轨运行中产生的遥测数据可能因为环境影响、部件故障等因素出现缺失和异常值，会对预测产生不良影响。数据预处理主要作用是对异常值和缺失值进行修正和填补。将偏差大于三倍标准差的值判断为异常值，筛选出异常值和缺失值后，将异常值视为缺失值，缺失值利用均值填补。

（2）ARIMA 建模。首先对输入的时间序列进行平稳性判断，如果该数据为平稳性数据，则继续后续步骤；如果不平稳，则对数据进行d阶差分直至平稳。绘制平稳数据的自相关图（ACF）和偏自相关图（PACF）判断截尾拖尾，得到参数p和q，以BIC 值为判断标准确定最佳参数，BIC 值越小，模型表现越好。利用定阶后的ARIMA 模型预测训练集数据，得到预测结果，计算残差

（3）SVR 残差预测。对于非线性模型，利用核函数映射到特征空间，然后进行回归。利用符号S表示SVR 模式的确定语句量，有

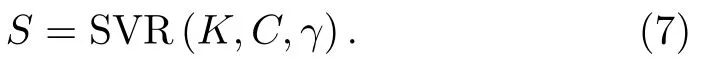
其中：K表示核函数类型，常用的核函数有线性核函数、径向基（高斯）核函数、多项式核函数；C为惩罚因子；γ为核函数的核系数，其值必须大于0。利用PSO寻优核函数参数，训练模型后获得残差预测值。

（4）将ARIMA 预测结果与SVR 残差预测结果结合，相加得到最终预测结果，即

模型预测效果的评价是整个模型预测的最后一步，通过评价标准判断模型优劣，从而得知该模型在本次预测中的适用性。模型预测误差越小，说明该模型的预测精度越高。常用的模型评价标准有多种，本文采用均方根误差（RMSE，定义符号ERMS）评价模型的预测效果。

RMSE 是预测值与真实值之间偏差的平方和与次数比值的平方根[12]，RMSE 值越小，效果越好。其计算公式为

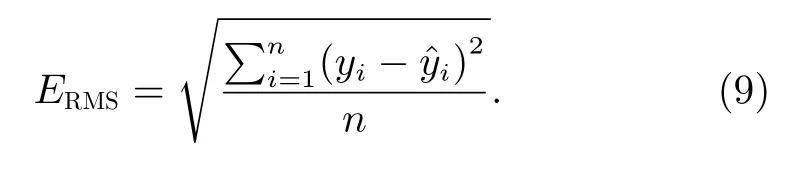
其 中，yi为真实值，为预测值。

3 实验验证

3.1 实验数据选取

卫星的星敏感器是卫星姿态控制系统的重要部件之一，星敏感器的温度变化会对卫星遥测数据产生影响，因此这里选择中国科学院先导专项KX09 卫星的星敏A 温度作为实验数据，分别进行短期和中期预测实验。目前通常要求卫星的监视预测需求为：短期预测时间为圈次级（每圈次90 min 左右，经历一次阳照区阴影区），一般为1～16 个圈次（1.5～10 h）；中期预测时间为天级（一般为1～7 天，每天约16 个圈次）。选取2020年9月20日21:51 LT 至2020年9月21日04:43 LT 连续100 条星敏A 温度数据，共计6 h 进行短期预测。卫星飞行一圈的时间约为90 min，样本数据的选取大约为卫星飞行4 圈的时间。按照4∶1 比例划分训练集与测试集，对数据进行预处理后绘出数据变化趋势，短期数据时序如图2所 示。

3.2 ARIMA 建模

如图2 所示，星敏A 为时间序列，对短期星敏A 的温度数据进行平稳性检测，可以看出该部分温度时序基本稳定，不需要差分。在判定温度数据时序稳定后，首先给出自相关和偏相关结果（见图3）。

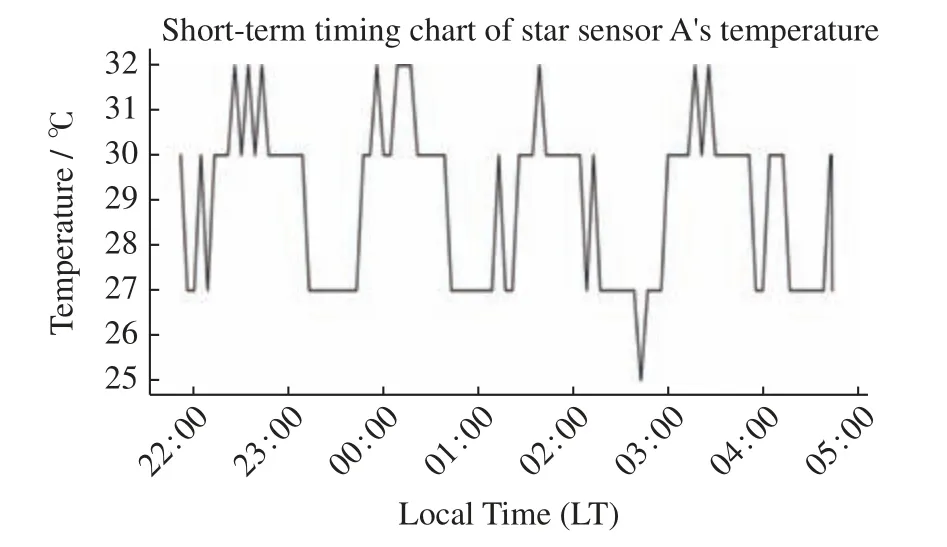
图2 2020年9月20日21:53 LT 至2020年9月21日04:43 LT KX09 星敏A 温度变化Fig.2 Temperature change of KX09 star sensor A from 20 September 2020 21:53 LT to 21 September 2020 04:43 LT

图3 中蓝色部分为置信区间，纵坐标分别为自相关及偏自相关系数。依据图3 中信息，初定模型为ARIMA(0,0,5)、ARIMA(2,0,0)以及ARIMA(2,0,5)。基于BIC 准则，选定BIC 值最小的ARIMA(2,0,5)为最佳模型。使用ARIMA(2,0,5)模型的初步预 测结果如图4 所示。

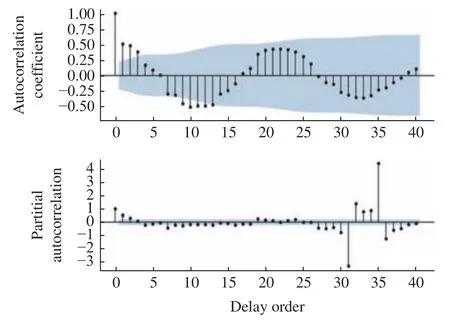
图3 星敏A 温度短期数据的自相关与偏相关结果Fig.3 Autocorrelation function and partial autocorrelation function of short-term temperature data of the star sensor A

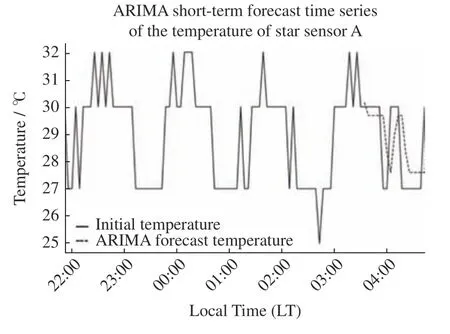
图4 2020年9月20－21日ARIMA 模型预测结果Fig.4 Results of ARIMA model prediction on 20－21 September 2020

3 .3 SVR 建模

3.3.1 SVR 核函数选择

对所选数据选择不同核函数，三种核函数的拟合效果如图5 所示。由图5 可以看出，径向基核函数（RBF）的拟合效果表现最好。为了验证观测结果的正确性，利用RMSE判别标准对三种核函数的拟合效果进行评价，结果列于表1。

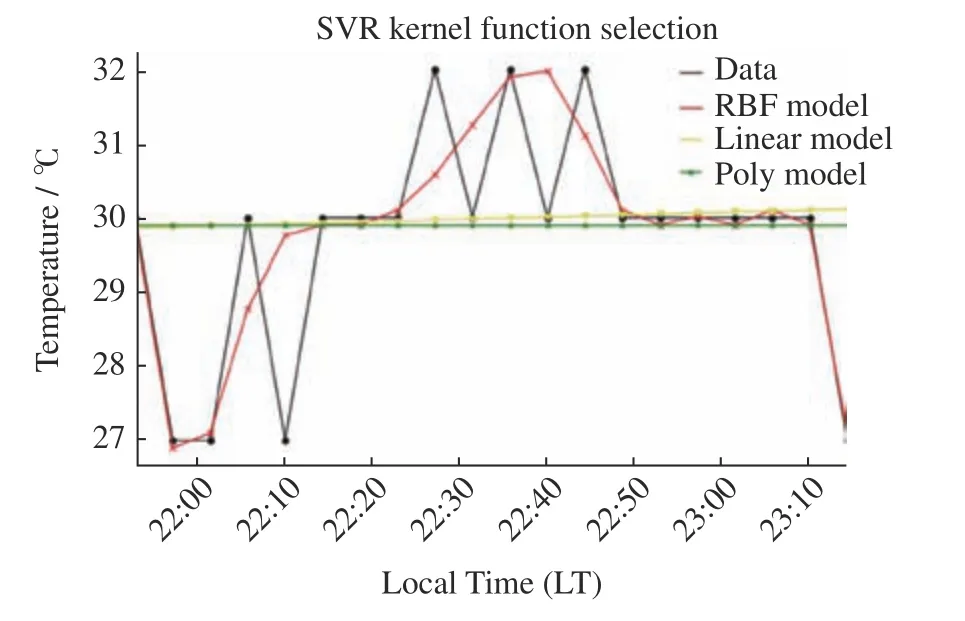
图5 2020年9月20日三种SVR 核函数拟合效果Fig.5 Fitting effect of three SVR kernel functions on 20 September 2020

由表1 可以看出，径向基核函数（RBF）的RMSE值最小，说明径向基核函数（RBF）在回归模型中的表现最好，在接下来的预测中，SVR 核函数的选择即为径 向基核函数（RBF）。

表1 三种核函数的RMSE 值对比Table 1 Comparison of RMSE of three kernel functions

3.3.2 核函数参数选择

径向基核函数中有两个参数C和γ。其中C为惩罚系数，γ为核函数的核系数，且γ值必须大于0。将原始数据与ARIMA 模型拟合数据作差，获取残差序列，将残差序列输入PSO 模型参数寻优，PSO 算法的参数设置见表2。寻优后的适应度函数如图6 所示，其中寻优后的C=7.14，γ=0.17。

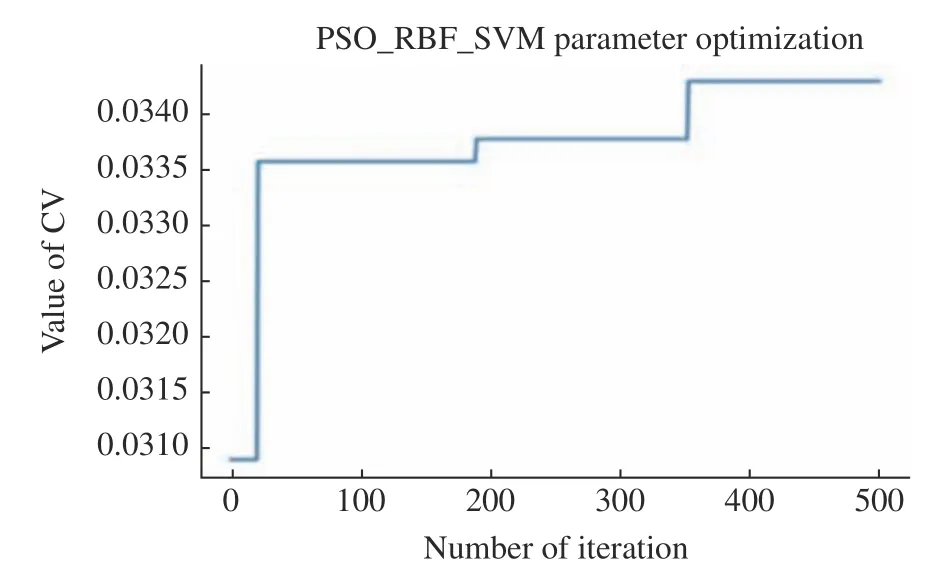
图6 短期温度序列的PSO 适应度函数曲线Fig.6 PSO fitness function curve of short-term temperature series

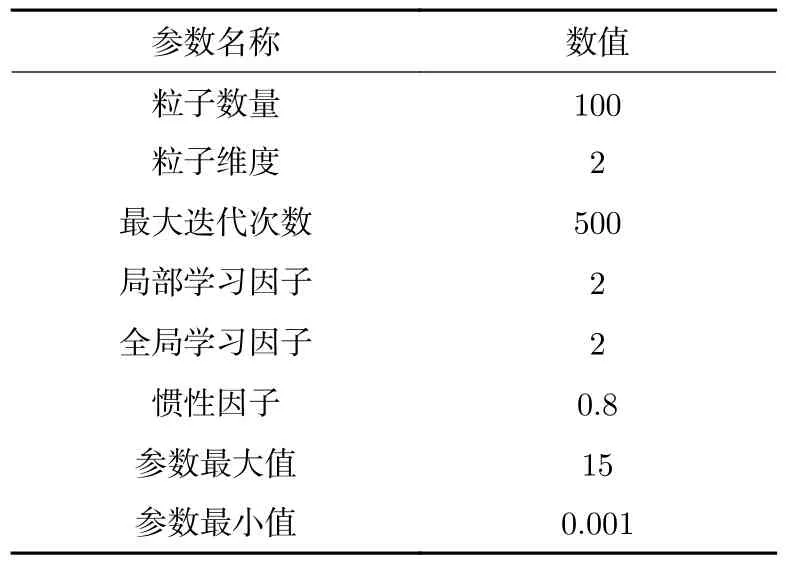
表2 PSO 算法参数设置Table 2 Parameter setting of PSO algorithm

将原始数据与ARIMA 初始预测数据的残差代入SVR 预测模型，SVR 参数C=7.14，γ=0.17，残差预测结果如图7 所示。

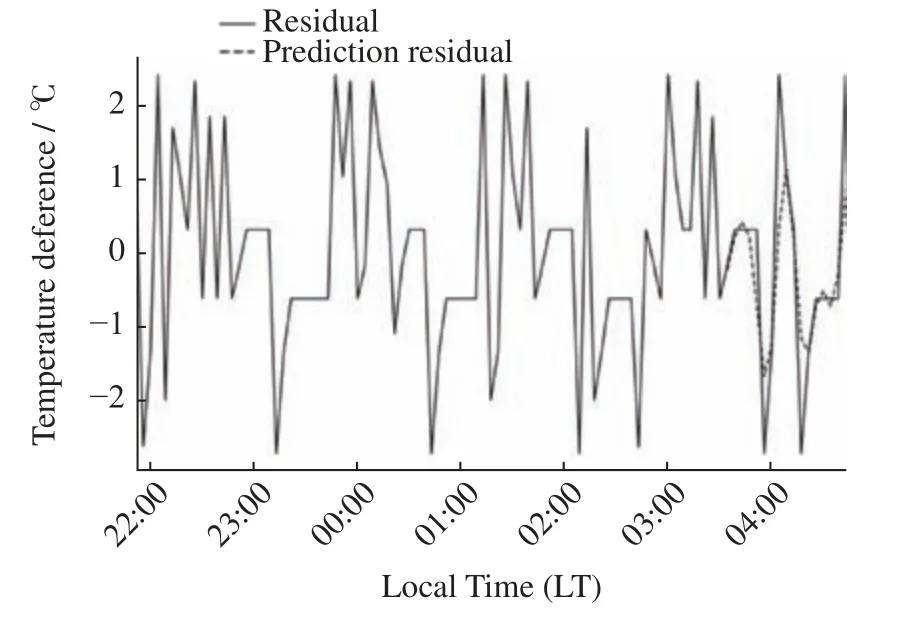
图7 2020年9月20－21日SVR 模型残差预测结果Fig.7 Results of SVR model residual prediction on 20－21 September 2020

将SVR 预测结果与ARIMA 预测结果相加，最终预测结果如图8 所示，从预测趋势可以看出组合模型 的拟合效果比单一ARIMA 模型表现好。

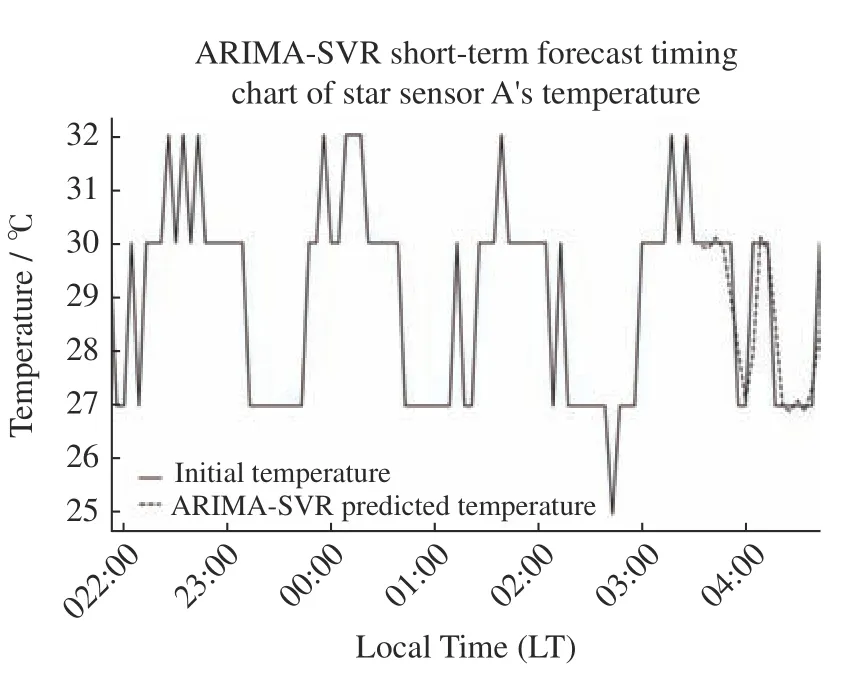
图8 2020年9月20－21日ARIMA-SVR组合模型预测结果Fig.8 Results of ARIMA-SVR combinational model prediction on 20－21 September 2020

3.4 预测结果及对比分析

本文还选取KX09 卫星2020年9月20日至9月30日共计10 天的星敏A 温度数据，利用同样方法进行中期预测。组合模型与单一ARIMA 模型短中期预测的RMSE 结果比较列于表3。可以看出：短期预测中，组合模型比单一ARIMA 模型的RMSE 提高了46.2%；中期预测中，组合模型比单一ARIMA 模型的RMSE 提高了16.4%。由RMSE 值可以看出，组合模型更适用于短期预测。

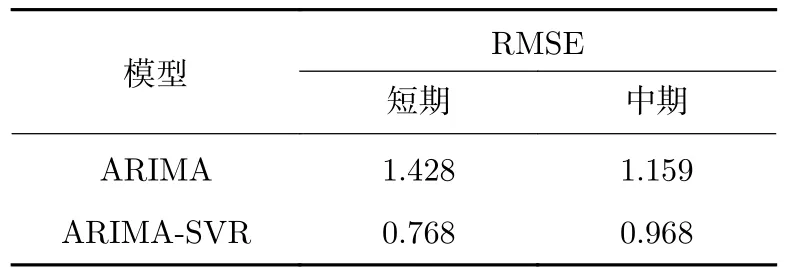
表3 温度预测结果RMSE 统计Table 3 RMSE statistics of prediction results of temperature

由于温度数据为平稳数据，为了验证组合算法的适用性，这里还利用卫星姿控系统中陀螺B的x轴角速度数据进行短中期预测。姿态控制系统是卫星姿态控制的重要部件，x、y、z轴的角速度与姿态控制密切相关。选择2021年1月18日05:38 LT 至2021年1月18日07:08 LT 卫星飞行一圈（90 min）共计450条数据进行角速度短期预测；选取2021年1月17日至2021年1月20日（3 天）共计10537 万条陀螺B的x轴角速度数据进行中期预测。短期角速度时序如图9 所示。

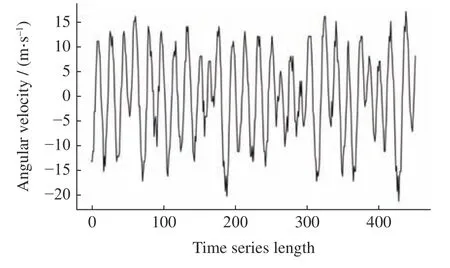
图9 陀螺B的x 轴角速度短期时序Fig.9 Short-term timing diagram of x-axis angular velocity of Gyro B

短期角速度序列经检验后确定为不平稳序列，需要对其做一阶差分后进行预测。依据温度预测步骤得出短中期预测结果，短中期预测的组合模型与单一ARIMA 模型预测的RMSE 结果比较列于表4。可以看出：短期预测中，组合模型比单一ARIMA 模型的RMSE 提高了71.2%；中期预测中，组合模型比单一ARIMA 模型的RMSE 提高了64.2%。由RMSE值 可以看出，组合模型更适用于短期预测。

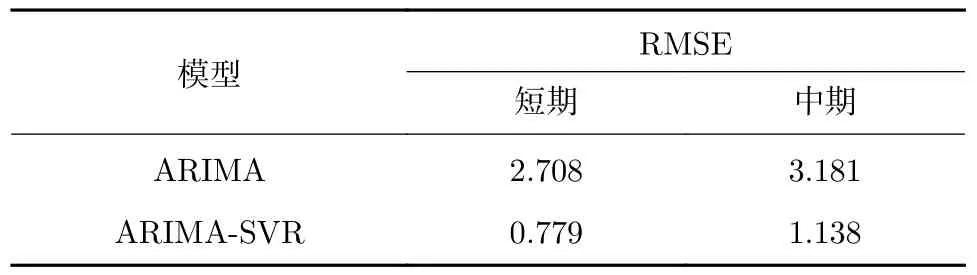
表4 角速度预测结果RMSE 统计Table 4 RMSE statistics of prediction results of angular velocity

4 结语

ARIMA 模型对不平稳时间序列的预测效果较好，但对于时间序列存在的非线性特征不能充分处理，因此利用SVR 模型补偿卫星遥测数据中的非线性特征，可以获得一种有效的非线性时间序列组合预测方法。本文利用ARIMA-SVR 组合模型对KX09卫星的星敏A 温度以及陀螺B的x轴角速度进行了短期和中期预测。在星敏A 温度的短期预测中，组合模型比单一ARIMA 模型的RMSE 提高了46.2%；中期预测中，组合模型比单一ARIMA 模型的RMSE提高了16.4%。在陀螺B的x轴角速度短期预测中，组合模型比单一ARIMA 模型的RMSE 提高了71.2%；中期预测中，组合模型比单一ARIMA 模型的RMSE提高了64.2%。实验证明该模型在卫星遥测数据的预测中具有实际应用价值，可用于卫星遥测数据趋势的预测，未来对卫星遥测数据预测进行研究时，可利用出现异常的数据，对异常数据进行预测，观察预测结果，分析异常的出现是否存在规律性。